复合材料是当前材料领域研究的热门,而三明治夹芯结构是复合材料一种较为常见的结构类型[1]。三明治结构通常由两层刚度较高的薄面板和轻质厚芯层焊接或者胶接形成,轻质和良好的力学特征使其在航空、船舶、汽车以及建筑等领域被广泛地使用。
由于软芯在厚度方向也很容易变形,所以软芯三明治梁是典型的二维结构。研究表明,由于不考虑厚度方向的变形,常用的梁理论包括欧拉-伯努利梁理论、铁摩辛柯梁理论和Reddy的三阶剪切变形梁理论均无法正确地描述软芯三明治梁的特性。新近发展的扩展高阶三明治梁理论 (Extended high order sandwich panel theory,EHSAPT)能够给出与三维弹性理论十分接近的结果[2-3],具有高的精度和普适性。但是,该理论公式非常复杂,目前仅有极少数情况获得了解析解,所以,必须借助于数值计算方法来求解EHSAPT在一般情况下的解。
结构分析中最常用的数值计算方法是有限元法[4-5],Yuan等人[6]基于EHSAPT建立了二节点的梁单元,给出了精度比较高的数值结果。弱形式求积单元法 (Weak form quadrature element method,QEM)是一种新的数值计算方法,其原理与有限元法一样,均是基于最小位能原理,所以被认为是一种高阶有限元法[7]。但是,由于采用了特殊的节点形式,QEM比常规的高阶有限元要高效得多。另外,由于在数值积分中借助了微分求积法(Differential quadrature method,DQM)导数的权系数公式[7],QEM的公式非常简洁,建立节点数目任意的单元方程也十分容易,所以是一种有应用前景并十分值得研究的数值计算方法。目前文献中已有了基于EHSAPT的弱形式求积三明治梁单元的研究报道[8-9]。
但是,前面提到的基于EHSAPT的研究报道仅涉及静力和自由振动分析,还没有见到涉及移动集中载荷作用下软芯三明治梁的动力响应问题的分析。虽然已有了成功采用DQM求解普通梁在移动点载荷作用下的动力响应问题的报道[10],但是,研究表明如果节点分布形式不当,会存在虚假的复模态,从而导致DQM得不到正确的解;另外,DQM在分析几何形状不规则问题时也存在困难,而弱形式的求积单元法可以克服DQM的这些缺点,所以本文采用QEM进行分析,给出了相应的公式和求解步骤,并对公式和编写的程序进行了验证,首次给出了软芯三明治梁在移动点载荷作用下的动力响应。
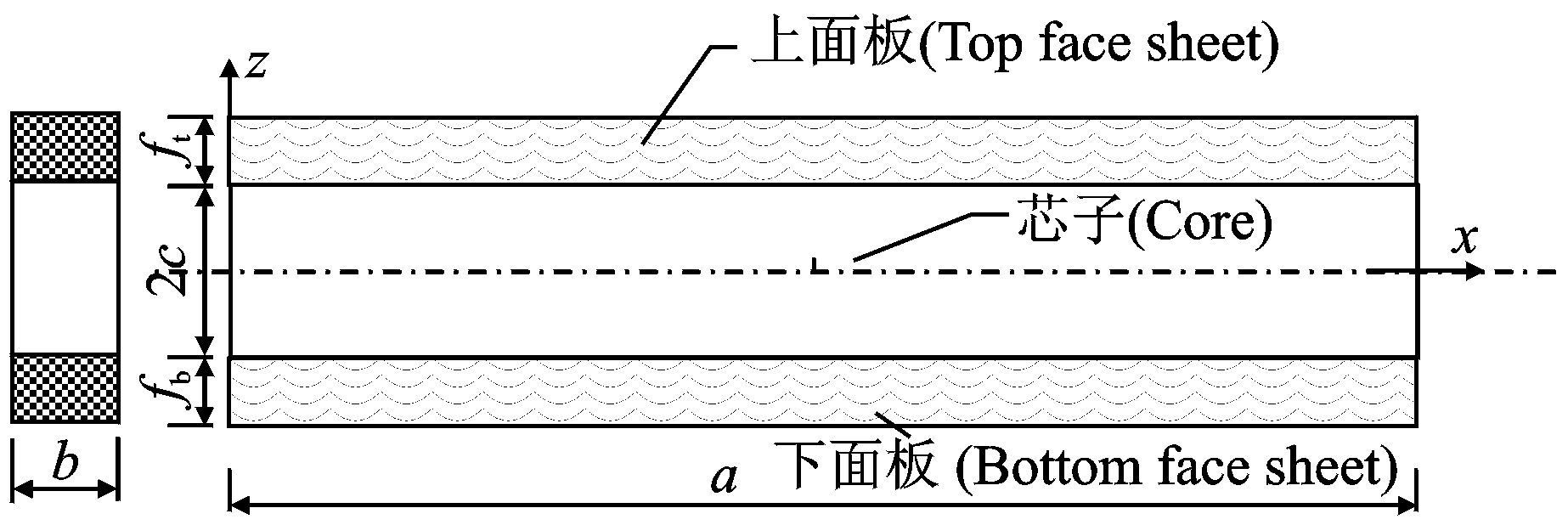
1 扩展的高阶三明治梁理论为了完整性,本节简要介绍扩展的高阶三明治梁理论[2, 3]。图 1给出了三明治梁示意图,包括本文后面用到的一些符号和坐标系。另外,后面出现的公式中的符号E,v,G和ρ分别代表弹性模量、泊松比、剪切模量和材料密度,u和w分别代表x和z方向的线位移,代表芯材中面的角位移,上标(或者下标)t,b,c分别代表上面板、下面板和芯子,而下标0代表上、下面板或芯子的中面。
|
图 1 三明治梁示意图 Figure 1 Sketch of a sandwich beam |
扩展的高阶三明治梁理论中,上下面板均采用欧拉-伯努利梁理论,芯子采用正交异性平面应力(平面应变)的二维板理论,芯子z向的位移假设为z的二次多项式,而x向的位移假设为z的三次多项式,然后利用上下交界面处的位移连续条件得出扩展的高阶三明治梁理论的位移场。位移场的具体表达式为
| $\left\{ \begin{align} & {{w}^{t}}\left( x,z,t \right)=w_{0}^{t}\left( x,t \right) \\ & {{u}^{t}}\left( x,z,t \right)=u_{0}^{t}\left( x,t \right)\text{ }-z-c-{{f}_{t}}2w_{0x}^{t}\left( x,t \right) \\ \end{align} \right.$ | (1) |
| $\left\{ \begin{align} & {{w}^{b}}\left( x,z,t \right)=w_{0}^{b}\left( x,t \right) \\ & {{u}^{b}}\left( x,z,t \right)=u_{0}^{b}\left( x,t \right)-z+c+\text{ }{{f}_{b}}2w_{0x}^{b}\left( x,t \right) \\ \end{align} \right.$ | (2) |
| $\left\{ \begin{align} & {{u}^{c}}\left( x,z,t \right)=z\left( 1-\frac{{{z}^{2}}}{{{c}^{2}}} \right)\phi _{0}^{c}\left( x,t \right)+\frac{{{z}^{2}}}{2{{c}^{2}}}\left( 1-\frac{z}{c} \right)u_{0}^{b} \\ & \left( x,t \right)+\left( 1-\frac{{{z}^{2}}}{{{c}^{2}}} \right)u~_{0}^{c}\left( x,t \right)+\frac{{{z}^{2}}}{2{{c}^{2}}}\left( 1+\frac{z}{c} \right)u_{0}^{t}\left( x,t \right)+ \\ & {{f}_{b}}{{z}^{2}}4{{c}^{2}}\times \text{ }-1+zcw_{0x}^{b}\left( x,t \right)+\frac{{{f}_{t}}{{z}^{2}}}{~4{{c}^{2}}}\left( 1+\frac{z}{c} \right)\times w_{0x}^{t}\left( x,t \right) \\ \end{align} \right.$ | (3) |
| $\left\{ \begin{align} & {{w}^{c}}\left( x,z,t \right)=\left( -\frac{z}{2c}+\frac{{{z}^{2}}}{2{{c}^{2}}} \right)w_{0}^{b}\left( x,t \right)+\left( 1-\frac{{{z}^{2}}}{~{{c}^{2}}} \right)\times \\ & w~_{0}^{c}\left( x,t \right)+\left( \frac{z}{2c}+\text{ }\frac{{{z}^{2}}}{2{{c}^{2}}} \right)w_{0}^{t}\left( x,t \right) \\ \end{align} \right.$ | (4) |
按照弹性力学的一般方法可以导出三明治梁的应变能、动能和外力做的功。引入量纲化一坐标ξ=2x/a-1,三明治梁应变能为
| $U={{U}^{t}}+{{U}^{b}}+{{U}^{c}}$ | (5) |
式中
| $\begin{align} & {{U}^{t,b}}=\frac{1}{2}\int_{0}^{a}{\left[ \frac{{{E}^{t,b}}f_{t,b}^{3}}{12} \right.}~{{\left( \frac{{{\partial }^{2}}{{w}^{~t,\text{ }b}}}{\partial x{{~}^{2}}} \right)}^{2}}+ \\ & {{E}^{t,b}}{{f}_{t,b}}\left. {{\left( \frac{\partial {{u}^{t,b~}}}{\partial x} \right)}^{2}} \right]dx=\frac{1}{2}\int_{-1}^{1}{\left[ \frac{{{E}^{t,b}}f_{t,b}^{3}}{12} \right.}\frac{8}{{{a}^{3}}}{{\left( \frac{{{\partial }^{2}}w{{~}^{t,b}}}{\partial {{\xi }^{2}}} \right)}^{2}}+ \\ & \frac{2{{E}^{t,b}}{{f}_{t\text{ },b~}}}{a}\left. {{\left( \frac{\partial {{u}^{t,b}}}{\partial \xi } \right)}^{2}} \right]d\xi \\ \end{align}$ | (6) |
| $\begin{align} & {{U}^{c}}=\frac{1}{2}\int_{0}^{a}{\left\{ \delta \left( x,t \right) \right\}}{{~}^{T~}}\left\{ \int_{-c}^{c}{{{\left[ B\left( z \right) \right]}^{T}}}\left[ D\text{ } \right]\left[ B\left( z \right) \right]dz \right\}\centerdot \\ & \left\{ \delta \left( x,t \right) \right\}dx=\frac{1}{2}{{\int_{-1}^{1}{\frac{a}{2}}}^{~}}\left\{ \delta \left( \xi ,t \right) \right\}{{~}^{T~}}T\left[ DD \right]\left\{ \delta \left( \xi ,t \right) \right\}d~\xi \\ \end{align}$ | (7) |
| $\begin{align} & {{\left\{ \delta \left( x,t \right) \right\}}^{T}}=[u_{0}^{t},u_{0x}^{t}~,w_{0}^{t},w_{0x}^{t},w_{0xx}^{t},u_{^{0}}^{c},u_{^{0x}}^{c},w_{0}^{c}, \\ & w_{0x}^{c},\varphi _{0}^{c},\varphi ~_{0x}^{c},u_{0}^{b},\text{ }u_{0x}^{b},w_{0}^{b},w_{0x}^{b},w_{0xx}^{b}] \\ \end{align}$ | (8) |
| $\left[ D \right]\text{ }=\left[ \begin{matrix} \frac{E_{x}^{c}}{1-\nu ~_{zx}^{2}E_{x}^{c}/E_{z}^{c}} & \frac{{{\nu }_{zx}}E_{z}^{c}}{1-\nu ~_{zx}^{2}E_{x}^{c}/E_{z}^{c}} & 0 \\ \frac{{{\nu }_{xz}}E_{x}^{c}}{1-\nu ~_{zx}^{2}~E_{x}^{c}/E_{z}^{c}} & \frac{E_{z}^{c}}{1-\nu ~_{zx}^{2}~E_{x}^{c}/E_{z}^{c}} & 0 \\ 0 & 0 & G_{xz}^{c} \\ \end{matrix} \right]$ | (9) |
三明治梁的动能为
| $\begin{align} & T=\frac{1}{2}\left\{ {{\int }_{{{V}_{t}}}}{{\rho }_{t}}(~\dot{u}_{t}^{2}~+\dot{w}_{t}^{2})dV+{{\int }_{{{V}_{b}}}}{{\rho }_{b}}({{{\dot{u}}}^{2}}_{b}+{{{\dot{w}}}^{2}}_{b})dV+{{\int }_{{{V}_{c}}}}{{\rho }_{c}}~({{{\dot{u}}}^{2}}_{c}+{{{\dot{w}}}^{2}}_{c})dV \right\} \\ & =\frac{1}{2}\int_{0}^{a}{{{\left\{ u\left( x,t \right) \right\}}^{T}}}\left[ \mu \right]\{u(x,t)\}dx \\ & =\frac{1}{2}\int_{-1}^{1}{\frac{a}{2}}\left\{ u\left( \xi ,t \right) \right\}{{~}^{T}}\left[ \mu \right]\left\{ u\left( \xi ,t \right) \right\}d\xi \\ \end{align}$ | (10) |
式中:位移上面的“·”是关于时间的一阶导数;
将式 (1~4) 代入式(10)可得到动能的具体表达式[3, 9]。考虑到梁受移动点载荷的动态响应只与梁的低阶振动模态和弯曲为主的振动模态相关,为了使矩阵[μ]成为对角矩阵以提高动力学响应的计算效率,芯子的位移场采用如下简化形式
| $\begin{align} & {{u}^{c}}\left( x,z,t \right)=u_{^{0}}^{c}\left( x,t \right)+\phi _{^{0}}^{c}\left( x,t \right)z, \\ & {{w}^{c}}\left( x,z,t \right)=w_{^{0}}^{c}\left( x,t \right) \\ \end{align}$ | (11) |
矩阵[μ]的对角元为
| $\begin{align} & {{\mu }_{1,1}}={{\rho }_{t}}b{{f}_{t}};{{\mu }_{2,2}}={{\rho }_{t}}b{{f}_{t}};{{\mu }_{3,\text{ }3}}={{\rho }_{b}}b{{f}_{b}}{{\mu }_{4,4}}= \\ & {{\rho }_{b}}b{{f}_{b}};{{\mu }_{5,5}}=2cb{{\rho }_{c}};\text{ }{{\mu }_{6,6}}=2cb{{\rho }_{c}};{{\mu }_{~}}_{7,7}=2{{c}^{3}}{{\rho }_{c}}b/3; \\ & {{\mu }_{8,8}}=f_{t}^{3}{{\rho }_{t}}b/12;{{\mu }_{9,9}}=f_{b}^{3}{{\rho }_{b}}b/12 \\ \end{align}$ | (12) |
需要说明的是,式(11)仅用于计算三明治梁的动能。
三明治梁顶部面板受移动集中载荷P作用时外力做的功为
| $W=P{{w}^{t}}\left( t \right)\text{ }0\le t\le a/\upsilon $ | (13) |
式中为集中载荷P移动的速度。
2 N节点三明治梁单元及运动方程的求解由于篇幅限制,而且文献[8]已给出了刚度矩阵的具体公式并验证了其正确性和计算效率,所以,本文仅给出其位移场并简要说明刚度矩阵的建立过程。
单元的节点采用GLL(Gauss Lobatto Legendre)[11]点,节点的量纲化一坐标值用ξi(i=1,2,…,N)表示,GLL点的值和对应的权系数可以从文献[7]附录I中得到。单元的位移场为
| $\begin{align} & u\left( \xi ,t \right)=\sum\limits_{j=1}^{N}{{{l}_{j}}}\left( \xi \right)u\left( {{\xi }_{j}},t \right)=\sum\limits_{j=1}^{N}{l{{~}_{j}}}\left( \xi \right){{u}_{j}}\left( t \right) \\ & w\left( \xi ,t \right)=\sum\limits_{j=1}^{N}{{{\varphi }_{j}}}\left( \xi \right)w({{\xi }_{j}},t)+{{\psi }_{1}}\left( \xi \right){{w}_{~}}x({{\xi }_{1}},t)+ \\ & {{\psi }_{N}}\left( \xi \right){{w}_{x}}\left( {{\xi }_{N}},t \right)=\sum\limits_{j=1}^{N+2}{{{h}_{j}}}{{\left( \xi \right)}_{j}}\left( \text{ }t \right) \\ \end{align}$ | (14) |
式中:u(ξ,t)代表ut(ξ,t),ub(ξ,t),uc(ξ,t)和$\phi $c(ξ,t);w(ξ,t)代表wt(ξ,t),wb(ξ,t)和wc(ξ,t);lj(ξ)和hj(ξ)分别为Lagrange和Hermite插值函数。
将式(14)代入式(5),采用GLL积分计算单元的刚度矩阵。积分计算时直接利用DQM的权系数显式表达式来计算位移在积分点处的各阶导数值,所以,不需要式 (14)的各阶导数的具体表达式,这与常规有限元的刚度矩阵的计算不同,使形成N(这里N可以任意变化)节点三明治梁单元的刚度矩阵变得十分容易。经过积分后单元的应变能可以表示为
| $U=\frac{1}{2}{{\left\{ \delta \left( t \right) \right\}}^{T}}\left[ k \right]\left\{ \delta \left( t \right) \right\}$ | (15) |
式中k为N节点三明治梁单元的刚度矩阵,单元的节点位移向量定义为
| $\begin{align} & \left\{ \delta \left( t \right) \right\}=[\delta _{u}^{t}\left( t \right),{{\delta }_{w}}^{t}(t),{{\delta }_{u}}^{b}(t),{{\delta }_{w}}^{b}\left( t \right), \\ & {{\delta }_{u}}^{c}(t),{{\delta }_{w}}^{c}\left( t \right),{{\delta }_{\varphi }}^{c}(t){{]}^{T}} \\ \end{align}$ | (16) |
式中:每个δwt(t),δwb(t)和δwc(t)向量中包含N+2个自由度;每个δut(t),δub(t),δuc(t)和δφc(t)向量中包含N个自由度,即单元的每一个内节点有7个自由度:u0t(t),w0t(t),u0b(t),w0b(t),u0c(t),w0c(t)和$\phi $c0(t),两个端点有10个自由度:u0t(t),w0t(t),w0xt(t),u0(t),w0b(t),wb0xb(t),u0c(t),w0c(t),w0xc(t)和$\phi $c0(t),所以单元总共有(7N+6)个自由度。
单元质量矩阵的推导与文献[9]中的一致质量矩阵不同,本文形成质量矩阵的位移函数全部采用式(14)中的u(ξ,t)的形式,即假设的位移场的形状函数全部采用Lagrange插值多项式。单元的动能可以表示为
| $T=\sum\limits_{i=1}^{9}{{{T}_{i}}}=\frac{1}{2}{{\left\{ \dot{\delta }\left( t \right) \right\}}^{T}}\left[ m \right]\text{ }\left\{ \dot{\delta }\left( t \right) \right\}$ | (17) |
式中m为N节点三明治梁单元的质量矩阵,本文称它为简化质量矩阵以区别于文献[9]中的一致质量矩阵,Ti的表达式如下
| $$\eqalign{ & {T_1} = {{{\rho _t}{f_t}ab} \over 4}\sum\limits_{k - 1}^N {{H_k}} {\left( {\dot u_k^t} \right)^2},{T_2} = {{{\rho _t}{f_t}ab} \over 4}\sum\limits_{k - 1}^N {{H_k}} {\left( {\dot w_k^t} \right)^2}, \cr & {T_2} = {{{\rho _b}{f_b}ab} \over 4}\sum\limits_{k - 1}^N {{H_k}} {\left( {\dot u_k^b} \right)^2},{T_4} = {{{\rho _b}{f_b}ab} \over 4}\sum\limits_{k - 1}^N {{H_k}} {\left( {\dot w_k^b} \right)^2}, \cr & {T_5} = {{c{\rho _c}ab} \over 4}\sum\limits_{k - 1}^N {{H_k}} {\left( {\dot u_k^c} \right)^2},{T_6} = {{c{\rho _c}ab} \over 2}\sum\limits_{k - 1}^N {{H_k}} {\left( {\dot w_k^c} \right)^2}, \cr & {T_7} = {{{c^3}{\rho _c}ab} \over 6}\sum\limits_{k - 1}^N {{H_k}} {\left( {\dot \varphi _k^c} \right)^2}, \cr & {T_8} = {{{\rho _t}f_t^3ab} \over {48}}\sum\limits_{k - 1}^N {{H_k}} {\left( {\sum\limits_{i = 1}^N {{A_{ki}}\dot w_i^t} } \right)^2}, \cr & {T_9} = {{{\rho _t}f_b^3ab} \over {48}}\sum\limits_{k - 1}^N {{H_k}} {\left( {\sum\limits_{i = 1}^N {{A_{ki}}\dot w_i^b} } \right)^2} \cr} $$ | (18) |
式中Akj为DQM一阶导数的权系数,其显式表达式为[7]
| $\begin{align} & {{A}_{kj}}=~{{\left. \frac{d{{l}_{j}}\left( \xi \right)}{dx} \right|}_{\xi ={{\xi }_{k}}}}=\frac{2}{a}\frac{~d{{l}_{j}}\left( \xi {{~}_{k}} \right)}{d\xi }= \\ & \frac{2}{a}\left\{ \begin{matrix} \underset{\underset{i\ne \text{ }k,j}{\mathop i=1}\,}{\overset{N}{\mathop \prod }}\,\left( {{\xi }_{k}}-{{\xi }_{i}} \right)\text{ }\underset{\underset{j\ne i}{\mathop i=1}\,}{\overset{N}{\mathop \prod }}\,\left( {{\xi }_{j}}~-{{\xi }_{i}} \right) & k\ne j \\ \sum\limits_{\underset{i\ne k}{\mathop{i=1}}\,}^{N}{\frac{1}{({{\xi }_{k}}-\text{ }{{\xi }_{i}})}} & k=j \\ \end{matrix} \right. \\ \end{align}$ | (19) |
从式(18)中的T8和T9表达式可以看出质量矩阵不是对角阵,但是与导数自由度相关的元素均是零,采用按行相加的技术后质量矩阵变成对角阵。
计算移动集中载荷P做的功时,位移函数也采用式(14)中的u(ξ,t)的形式,所以有
| $\begin{matrix} W=P{{w}^{t}}\left( \upsilon t \right)=P\sum\limits_{j=1}^{N}{{{l}_{j}}}\left( 2\upsilon t/a-1 \right){{w}^{t}}_{j}=\sum\limits_{j=1}^{N}{{{f}_{j}}}w_{j}^{t} \\ 0\le t\le L/\upsilon \\ \end{matrix}$ | (20) |
根据Hamilton原理,三明治梁单元的运动方程可以表示为
| $\left[ m \right]\left\{ \ddot{\delta }\left( t \right) \right\}+\left[ k \right]\left\{ \delta \left( t \right) \right\}=\left\{ f\left( t \right)\text{ } \right\}$ | (21) |
施加位移边界条件和消去非零的导数自由度后,式(21)可以改写为
| $\left[ m \right]\left\{ \ddot{\delta }\left( t \right) \right\}+\left[ k \right]\left\{ \delta \left( t \right) \right\}=\left\{ f\left( t \right)\text{ } \right\}$ | (22) |
这样式(22)可以方便地用中心差分法求解。
具体的逐步积分公式为[12]
| $\begin{align} & \frac{1}{\Delta {{t}^{2}}}\left[ m \right]{{\left\{ \delta \right\}}_{t+\Delta t}}={{\left\{ f \right\}}_{t}}-\left( \left[ k \right]-\frac{2}{\Delta {{t}^{2}}}\left[ m \right] \right){{\left\{ \delta \right\}}_{t}}- \\ & \frac{1}{\Delta {{t}^{2}}}\left[ m \right]{{\left\{ \delta \right\}}_{t-\Delta t}} \\ \end{align}$ | (23) |
或者
| $\begin{align} & {{\left\{ \delta \right\}}_{t+\Delta t}}=\text{ }\left( \Delta {{t}^{2}}{{\left[ m \right]}^{-1}} \right)\left( {{\left\{ f \right\}}_{t}}-\left[ k \right]{{\left\{ f \right\}}_{t}} \right)+ \\ & 2{{\left\{ \delta \right\}}_{t}}-\left\{ \delta \right\}{{~}_{t-\Delta t}} \\ \end{align}$ | (24) |
式中:Δt为时间步长;对角矩阵[m]-1的主元为1/mii(i=1,2,…,NN),NN与边界条件有关。
3 算例与讨论用符号S,F和C分别代表简支、自由和固支边界。简支边界条件为:在x=0或a处有wt(x,t)=wb(x,t)=wc(x,z,t)=0;自由边界没有位移边界条件;固支边界条件为:在x=0或a处有wt(x,t)=wb(x,t)=wc(x,z,t)=u0t(x,t)=u0b(x,t)=u0c(x,t)=wxt(x,t)=wbx(x,t)=$\phi $0c(x,t)=0。
为了比较,梁的几何尺寸(除了梁的宽度b以外)和材料参数均取自文献[3, 9],如表 1所示。需要说明的是梁的宽度不影响最终的结果。由于篇幅限制,本文仅给出两个算例。
例1 三种不同边界(S-S,C-C,F-F)软芯三明治梁的自由振动分析。算例1用来验证简化质量矩阵的正确性和有效性。
对于自由振动分析,式(22)中的{f(t)}={0}并且{δ(x,t)}={Δ(x)}sinωt,其中ω为圆频率。方程(22)可以改写成下面的形式
| $\left[ k \right]\left\{ \Delta \right\}={{\omega }^{2}}\left[ m \right]\left\{ \Delta \right\}$ | (25) |
文献[8~9]已分别验证了单元的刚度矩阵和一致质量矩阵的正确性和有效性。研究表明,当N>15时弱形式的求积单元法可以给出相当精确的位移、应力分布、固有频率和固有模态。采用一个21节点的单元进行分析,结果比较如表 2所示。从表 2可以看出,本文的简化质量矩阵也能够给出精确的前六阶非零频率,与文献[9]采用精确的一致质量矩阵得到的结果之间的误差均小于2%,从而验证了简化质量矩阵的正确性和有效性。
| 表 1 软芯三明治梁的几何尺寸和材料性能 Table 1 Geometry and material properties of sandwich beam with soft core |
| 表 2 不同边界三明治梁的前六阶非零频率的比较 Table 2 Comparisons of the first six non-zero frequencies of sandwich beams with different boundary conditions |
例2 移动集中载荷(P=100N)作用下两端固支(C-C)软芯三明治梁的动力响应分析。点载荷P从x=0以速度移动到x=a,初始条件为
| $\begin{matrix} \left\{ \begin{align} & u_{0}^{t}\left( x,0 \right)=w_{0}^{t}\left( x,0 \right)=u_{0}^{b}\left( x,0 \right)=~w_{0}^{b}\left( x,0 \right)= \\ & u_{0}^{c}\left( x,0 \right)=w_{0}^{c}\left( x,0 \right)=\varphi _{0}^{c}\left( x,0 \right)=0 \\ & \dot{u}_{0}^{t}\left( x,0 \right)=\dot{w}_{0}^{t}\left( x,0 \right)=\dot{u}_{0}^{b}\left( x,0 \right)=\dot{w}_{0}^{b}\left( x,0 \right)= \\ & \dot{u}_{0}^{c}\left( x,~0 \right)=\dot{w}_{0}^{c}\left( x,0 \right)=\dot{\varphi }_{0}^{c}\left( x,0 \right)=0 \\ \end{align} \right. \\ 0\le x\text{ }\le a \\ \end{matrix}$ | (26) |
定义α=T1/2τ,T1=1.0/845.7 s,τ=a/,这里845.7/s是C-C软芯三明治梁的基频(表 2)。另外,定义顶部面板中点(x=a/2)处的挠度的动态放大因子Wam为
| $\begin{matrix} {{W}_{am}}=w_{0}^{t}\left( x=a/2,t \right)/0.357 & 0 <t\le \tau \\ \end{matrix}$ | (27) |
式中0.357 mm为C-C软芯三明治梁在顶部面板中点受相同集中载荷作用时顶部面板中点的挠度。
计算时统一取Δt=τ/100000。采用一个N节点的单元进行分析,为了验证单元的收敛性,节点数取值为11~21,参数α分别取0.25,0.50,0.75和1.00。计算得到的三明治梁上面板中点(x=a/2)处挠度动态放大因子Wam的最大值列于表 3。
| 表 3 两端固支三明治梁上面板中点处挠度动态放大因子的最大值 Table 3 Maximum dynamic magnification fact or of top face center deflection of C-C sandwich beam |
从表 3可以看出,本文建立的弱形式的求积单元法具有计算精度和效率高的优点,参数α越大(即速度越高),收敛越快,当N>15时弱形式的求积单元法可以给出相当精确的动态放大因子,所以,后面均采用一个21节点的单元进行分析。另外,三明治梁上面板中点挠度的最大的动态放大因子并不是随速度的增加而一直增加。
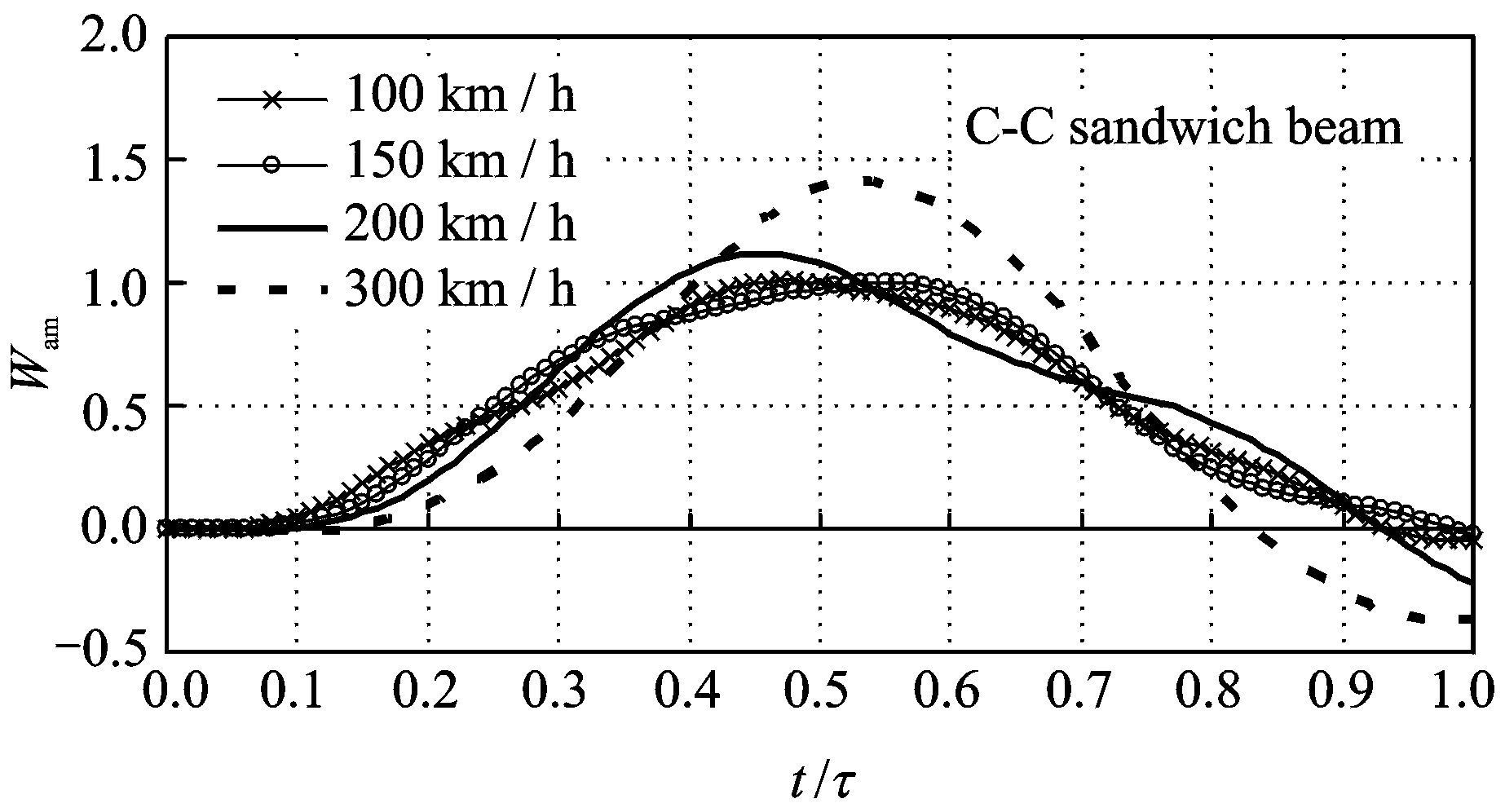
图 2给出了4种不同移动速度上面板中点处的挠度的动态放大因子Wam随时间 (t/τ) 的变化。4种不同移动速度分别对应于100,150,200和300 km/h。可以看出,在300km/h速度内,速度越高,动态放大因子的最大值似乎也越大。但是,实际上动态放大因子的变化非常复杂,除了与载荷的移动速度有关外还与三明治梁的边界条件、几何尺寸和材料性能等因素有密切关系。
|
图 2 不同移动速度下Wam随时间变化图 Figure 2 Variations of Wam with time for load at different speeds |
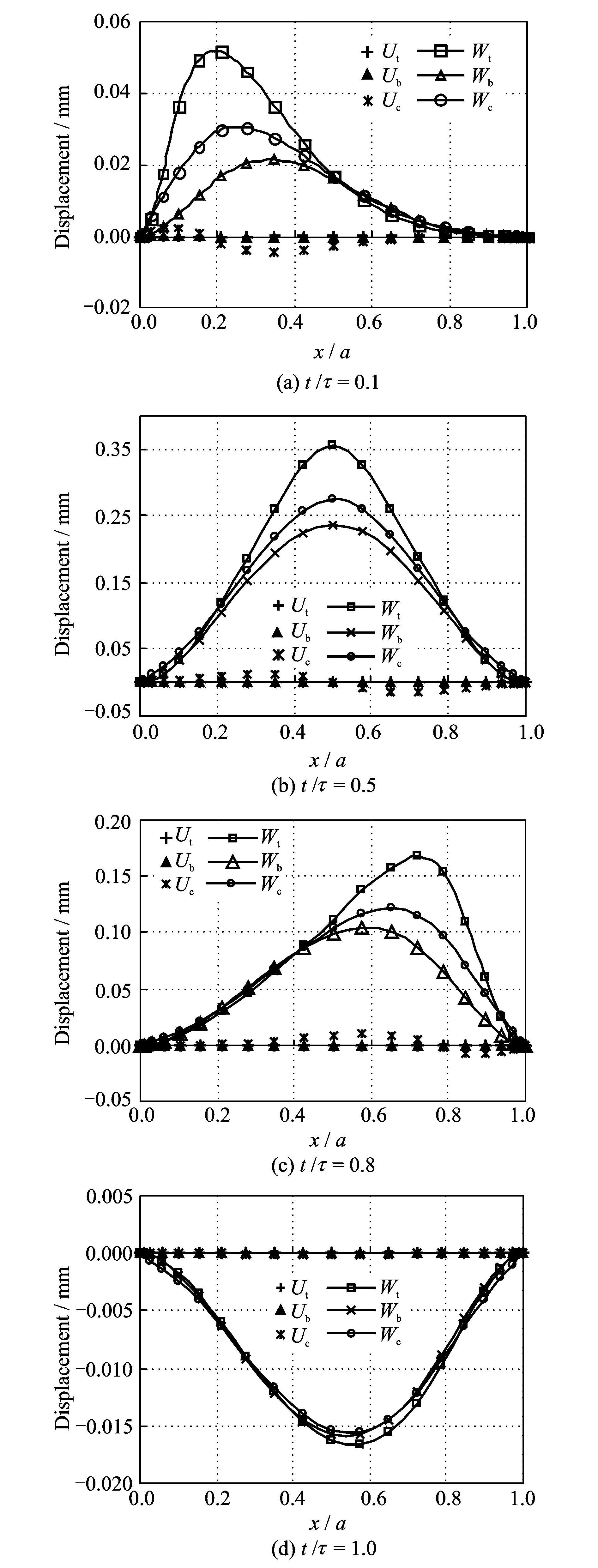
图 3给出了两端固支软芯三明治梁在100 km/h速度移动的点载荷作用下4个不同时刻的变形图。为了简化,图中各位移的下标0已被删除。可以看出:三明治梁轴向位移比横向挠度要小得多;由于芯材比较软,载荷又作用在上面板,所以上、下面板和芯材的横向挠度不同,上面板的横向挠度最大,芯材的横向挠度其次,而下面板的横向挠度最小。当载荷移动到梁中间时(图 3(b)),三明治梁的横向变形基本上是对称的。另外,当载荷移出梁时(图 3(d)),与静力问题不同的是三明治梁仍然有挠度,这时,上、下面板和和芯材的横向挠度基本相同,等同于横向自由振动。
|
图 3 两端固支软芯三明治梁在不同时刻的变形图 ( |
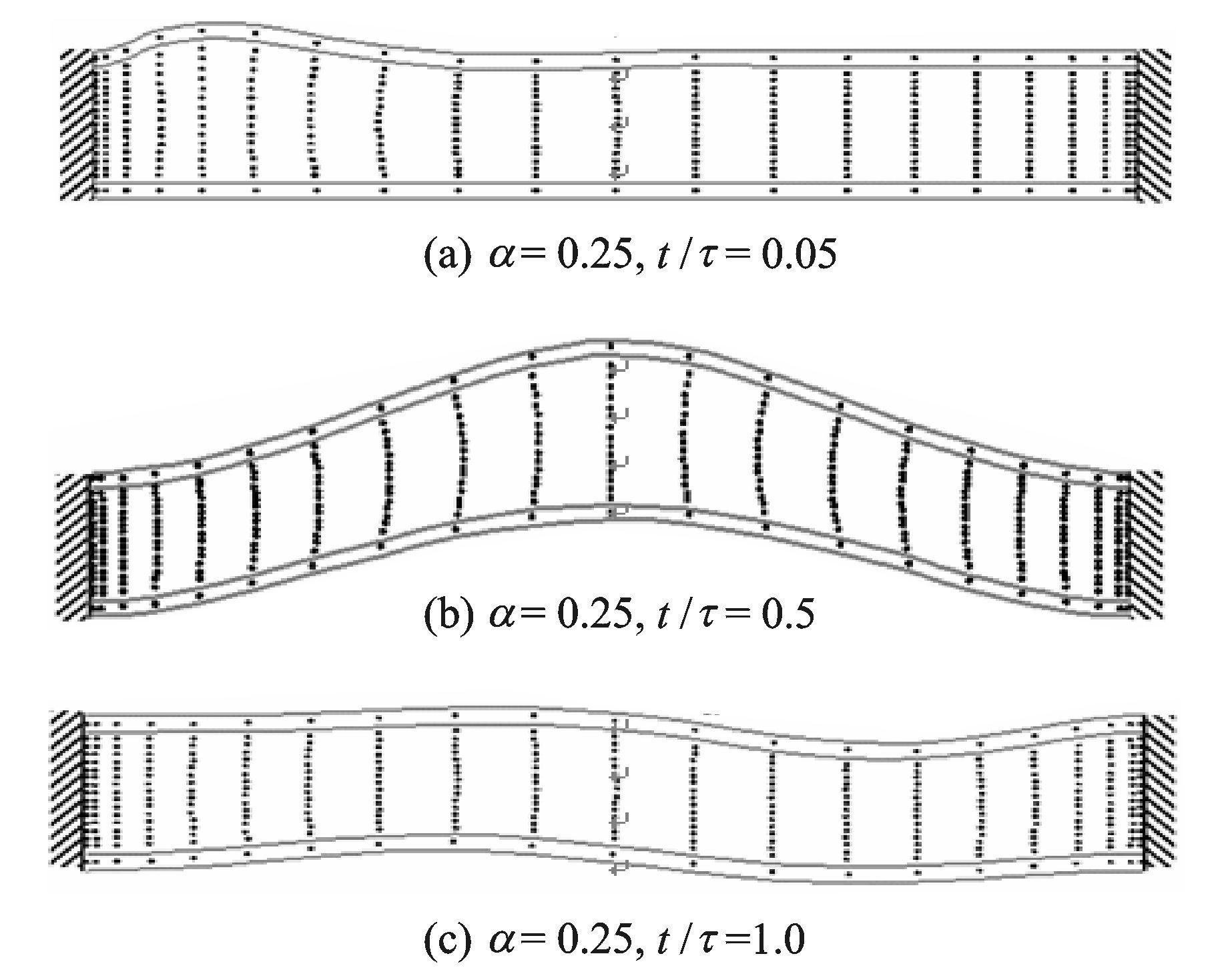
为了直观和清楚起见,图 4给出了两端固支三明治梁受移动点载荷作用时的变形随着时间变化的二维图,图 4(a,c)中的位移放大了1 000倍,而图 4(b) 中的位移放大了100倍,参数α取0.25,其对应的速度为
|
图 4 两端固支软芯三明治梁受移动载荷作用时的二维变形图( |
4 结束语
本文基于扩展的高阶三明治梁理论和Hamilton原理,建立了任意节点的弱形式求积梁单元,利用微分求积法导数的权系数显示表达式给出了单元刚度矩阵和质量矩阵的公式,同时给出了求解软芯三明治梁在移动集中载荷作用下的动力响应的步骤。本文先验证了建立的刚度矩阵和质量矩阵的正确性和方法的有效性,结果表明弱形式的求积单元法具有精度和计算效率高的优点,一个21节点的弱形式的求积梁单元就能够给出精度高的结果,采用简化质量矩阵也能够给出比较精确的软芯三明治梁的前六阶非零频率。然后采用中心差分法,首次给出了两端固支软芯三明治梁在移动集中载荷的动力响应,所得的结果可以供研究和工程设计人员参考。本文的研究拓展了弱形式求积法的应用范围
| [1] | Librescu L, Hause T. Recent developments in the modeling and behavior of advanced sandwich constructions: A survey[J]. Composite Structures , 2000, 48 (1/2/3) : 1–17. |
| [2] | Phan C, Frostig Y, Kardomateas G. Analysis of sandwich beams with a c ompliant core and with in-plane rigidity—Extended high-order sandwich panel t heory versus elasticity[J]. Journal of Applied Mechanics , 2012, 79 (4) : 041001–1. DOI:10.1115/1.4005550 |
| [3] | Frostig Y, Phan C, Kardoma teas G. Free vibration of unidirectional sandwich panels, Part I: Compressible c ore[J]. Journal of Sandwich Structures & Materials , 2013, 15 (4) : 377–411. |
| [4] |
袁慎芳, 闫美佳, 张巾巾, 等.
一种适用于梁式机翼的变形重构方法[J]. 南京航 空航天大学学报 , 2014, 46 (6) : 825–830.
Yuan Shenfang, Yan Meijia, Zhang Jinjin, et al. Shap e reconstruction method of spar wing structure[J]. Journal of Nanjing Aeronau tics & Astronautics , 2014, 46 (6) : 825–830. |
| [5] |
陈树霖, 刘莉, 董威利.
月球探测 器着陆腿动力学建模与仿真[J]. 南京航空航天大学学报 , 2014, 46 (3) : 4–474.
Chen S hulin, Liu Li, Dong Weili. Dynamics modeling and simulation for landing legs of lunar lander[J]. Journal of Nanjing Aeronautics & Astronautics , 2014, 46 (3) : 4–474. |
| [6] | Yuan Z, Kardomateas G, Frostig Y. Finite element formulation bas ed on the extended high-order sandwich panel theory[J]. AIAA Journal , 2015, 5 : 3. |
| [7] | Wang X. Differential quadrature and differential quadra ture based element methods: Theory and applications[M]. Waltha m, MA, USA: Elsevier Inc, 2015 . |
| [8] | Wang Y, Wang X. Static analysis of higher order sandwich beams by weak form quadrature element method[J]. Composite Structure s , 2014, 116 : 841–848. DOI:10.1016/j.compstruct.2014.06.015 |
| [9] | Wang Y, Wang X. Free vibration analysis of sof t-core sandwich beams by the novel weak form quadrature element method[J]. J o urnal of Sandwich Structures and Materials , 2016, 18 (3) : 294–320. DOI:10.1177/1099636215601373 |
| [10] | Wang X, Jin C. Differential quadrature analysis of moving load problem s[J]. Advances in Applied Mathematics and Mechanics , 2016, 8 (4) : 536–555. DOI:10.4208/aamm.2014.m844 |
| [11] | Kudela P, Krawczuk M, Ostachowicz W. Wave propagation mode lin g in 1D structures using spectral finite elements[J]. Journal of Sound and Vi bration , 2007, 300 : 88–100. |
| [12] |
刘剑.求解动力学问题的微分求积法研究[D].南京:南京航空航天 大学,2008. Liu Jian. On the differential quadrature method for a nalyzing dynamic problems[D]. Nanjing: Nanjing University of Aeronautics and A stronautics, 2008. |
 2016, Vol. 48
2016, Vol. 48


