2. 西北工业大学航空学院,西安,710072 ;
3. 西北工业大学无人机所,西安,710065
2. College of Aeronautics, Northwestern Polytechnical Univer sity, Xi′an, 710072, China ;
3. UAV Research Institute, Northwestern Polytechnical University, Xi′an, 710065, China
抖振是气流分离引起随机激励响应,抖振研究可分为:低速抖振和跨音速激波抖振。对于抖振现象的研究主要包括两个方面:抖振始发迎角的预测和抖振载荷的计算,抖振研究主要有抖振始发边界和抖振响应两方面。早期的抖振研究主要是采用实验手段,即基于风洞试验方法可准确预计飞行器抖振边界等,但该方法周期长且费用高,不适用无人机或者飞行器初始研制阶段采用;近些年随着计算方法的发展,采用数值理论计算研究抖振问题已经成为可能,抖振边界数值仿真预计的研究越来越得到重视。郭同庆等[1]对跨音速机翼抖振迎角估计。吕志咏等[2]研究双立尾-三角翼布局的立尾抖振实验。黄江涛等[3]建立了基于MDDES的分离流非定常数值模拟方法,耦合气动结构方程对某战斗机大攻角下边条涡干扰引起的垂尾抖振问题进行研究。韩冰等[4]采用耦合RANS方程及结构运动方程模拟了涡破裂诱导的垂尾简化模型抖振。李劲杰等[5]利用激光片光源显示实验对边条翼双垂尾布局模型流场进行研究。Kandil等[6-8]研究马赫数对垂尾抖振的影响。Morton等[9]基于DES紊流模型数值模拟了F-18大迎角状态下的垂尾抖振响应。Healey[10]对F-18垂尾疲劳测试。Steimle等[11]研究了后掠翼的抖振机理。
目前大多数抖振边界预计研究是针对跨音速抖振边界的预测,且大多集中于二维翼型,对于着陆状态下无人机的低速抖振边界预计问题还未见涉及[12-13]。首先基于RANS方程和SST湍流模型采用升力系数判据、俯仰力矩系数判据及极限流判据等方式计算刚性飞翼无人机在低速大迎角状态下的抖振始发迎角;然后基于RANS方程和CFD/CSD耦合技术[14]研究飞翼无人机在抖振始发迎角附近的抖振载荷响应。
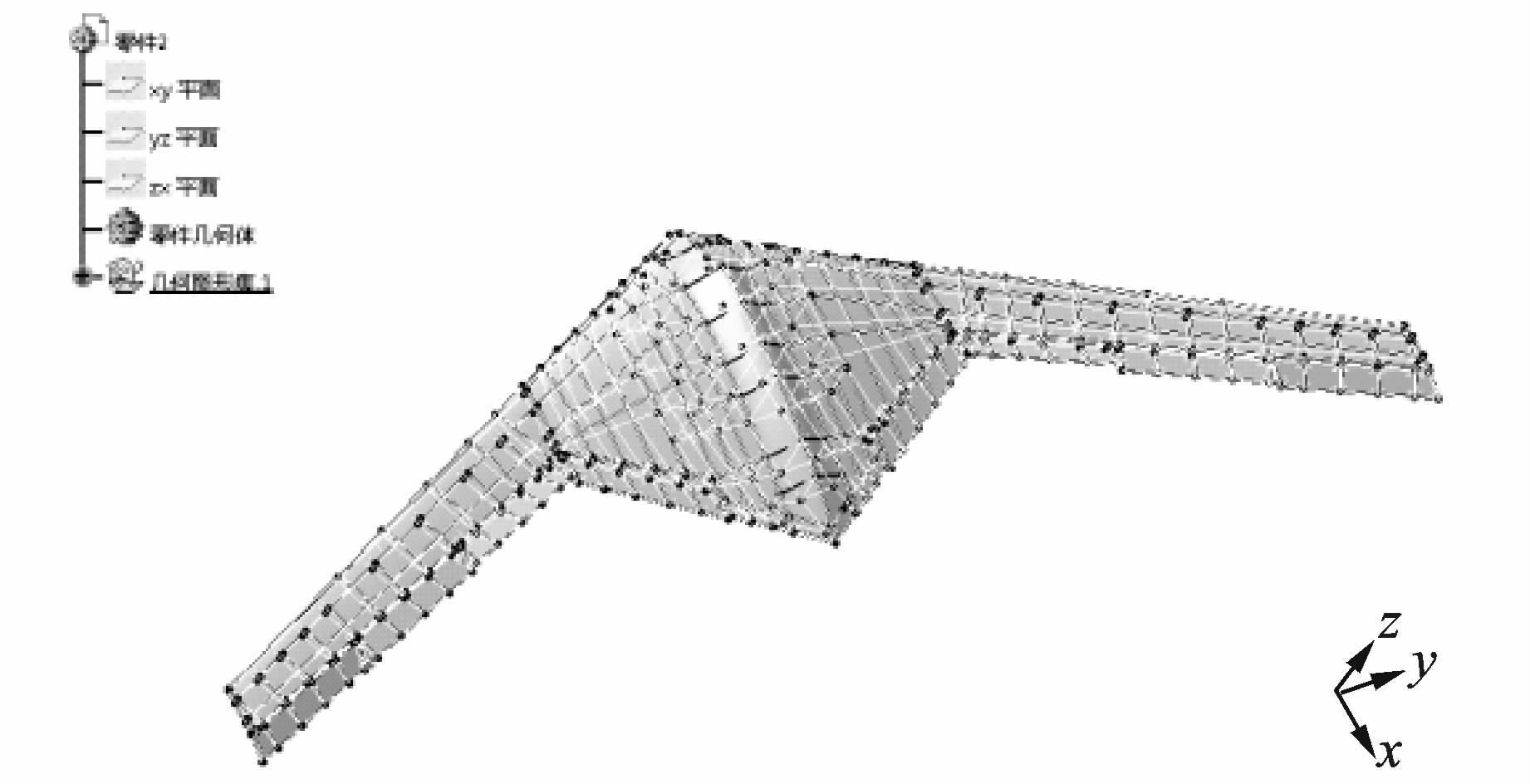
1 飞翼式无人机模型飞翼式无人机模型如图 1所示,无尾飞翼式无人机采用内、外翼飞翼式布局,l=15m,S=23.5m2,c=1 661.1mm,无尾飞翼无人机模型如图 1所示。
|
图 1 飞翼式无人机模型 Figure 1 Geometry model of flying-wing UAV |
2 抖振始发迎角预测
本节首先对飞翼无人机低速飞行状态下抖振边界进行预测,采用Fluent软件基于RANS方程和SST湍流模型,根据升力特性曲线判据、俯仰力矩特性曲线判据及表面流线判据这3种判据来预测飞翼无人机在低速大迎角飞行时的抖振始发迎角[1]。采用非结构气动网格基于RANS方程和二方程的SST湍流模型进行气动力的计算,初始计算状态的计算参数如下:H=0.2 km,Ma∞=0.18,Re=6.847×106。飞翼无人机半模的相关参数如下:S=11.75 m2,c=1.6 m。
2.1 表面极限流判据预测产生抖振的直接原因是机翼表面的气流发生分离。
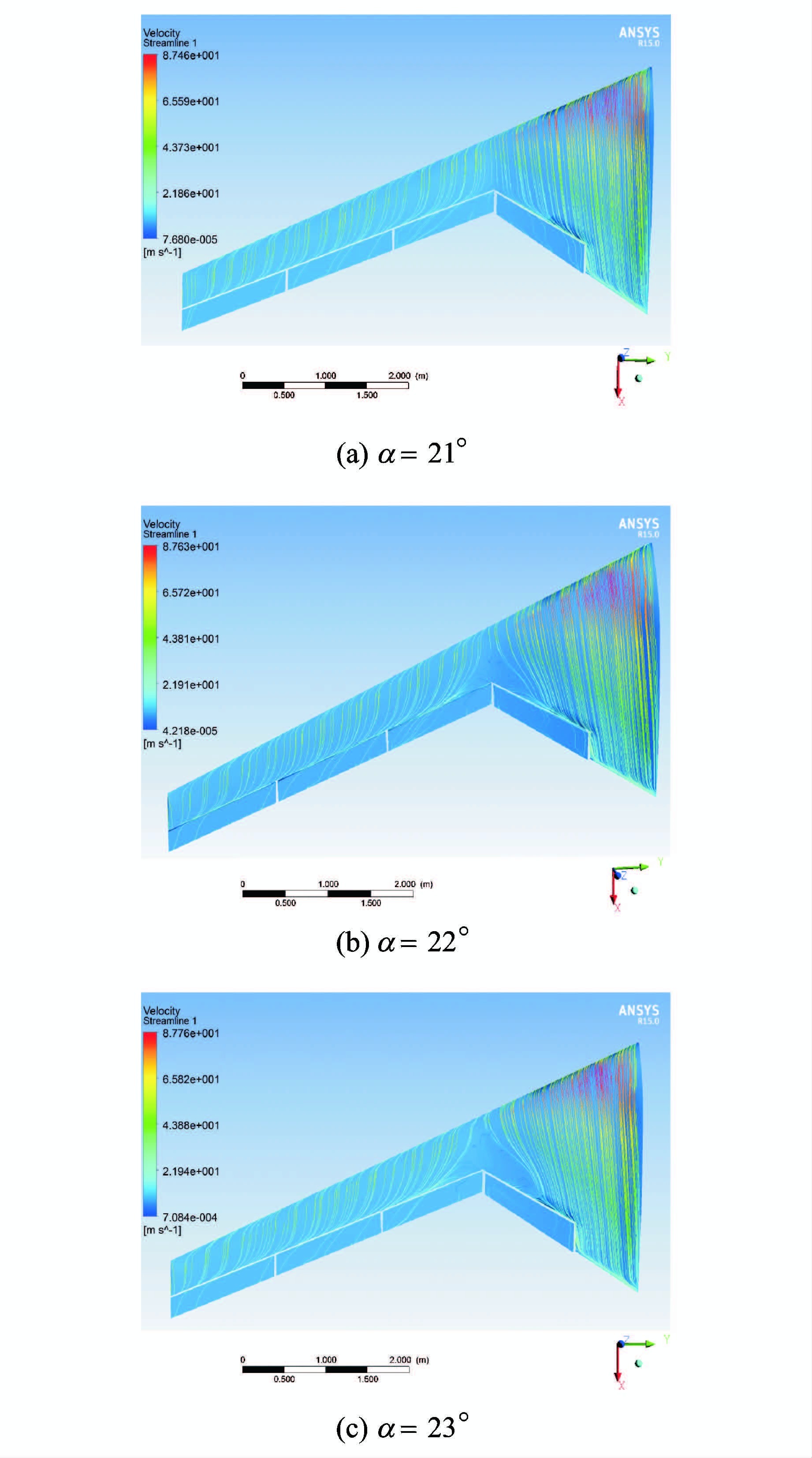
图 2给出了不同迎角状态下飞翼布局无人机表面极限流线分布情况。从图 2可看出各翼面上气流分离随着迎角变化的情况如下:当迎角α=21°,即如图 2(a)中所示主翼面和方向舵、升降舵上的流线都没有表现出比较明显的气流分离特征。
|
图 2 不同迎角下表面极限流 Figure 2 Surface limit flow at different angles |
2.2 俯仰力矩系数判据预测
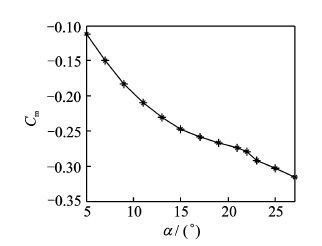
图 3给出了低速状态下飞翼布局无人机俯仰力矩系数Cm随迎角变化曲线。从图中可看出:在给定计算条件下,随着迎角的增大,俯仰力矩系数整体幅值有负增长的趋势且呈现有典型的转折,这主要是因为纵向稳定性损失引起的,翼面出现气流分离,无人机出现抖动,可以将俯仰力矩变化失稳转折点定义为抖振边界的始发迎角。从俯仰力矩曲线图中可看出:给定计算状态下飞翼布局无人机的抖振始发迎角为α=22°;在抖振始发迎角附近俯仰力矩曲线变化特征较为明显,因此俯仰力矩曲线判据作为抖振边界的预测估计更容易。
|
图 3 俯仰力矩系数曲线 Figure 3 Pitching moment coefficient figure |
2.3 升力系数判据预测
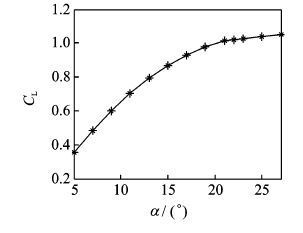
图 4给出了低速状态下飞翼布局无人机升力系数CL随迎角变化曲线。从图中可看出:在给定计算状态下,随着迎角的变化,升力系数随着迎角的增加基本呈现线性增长趋势,但当迎角增大到一定值时,无人机表明出现气流分离区,升力线斜率有些减小,无人机出现轻微的抖振。从图 4还可看出:当迎角为α=22°时,升力系数曲线斜率有些减小,因此通过升力系数曲线可预测无人机的抖振边界的始发迎角为α=22°。
|
图 4 升力系数系数随迎角变化曲线 Figure 4 Lift moment coefficient figure |
3 CFD/CSD抖振载荷计算
气动结构耦合作用仅发生在两者的耦合交界面上,因此气动结构耦合问题可表示为
| $M\ddot{U}+C\dot{U}+KU=F\left( t \right)$ | (1) |
| ${{\frac{\partial }{\partial t}}_{\Omega }}\overline{Q}d\Omega +\left( \overline{G}+Q{{q}_{b}} \right)\centerdot dS={{\frac{1}{\operatorname{Re}}}_{S}}{{\overline{F}}^{V}}\centerdot dS$ | (2) |
| ${{\sigma }_{s}}\centerdot n=-pn,{{u}_{s}}={{u}_{F}}$ | (3) |
式(1)为结构动力学方程;式(2)为积分形式的非定常N-S方程组;式(3)为耦合面的条件。基于RANS方程和CFD/CSD耦合技术研究飞翼无人机在抖振始发迎角附近的抖振载荷响应,并分别在时频域内分析飞翼无人机的抖振载荷响应特性。飞翼无人机气动结构耦合抖振载荷的计算采用半模,基于较为详细的结构模型和气动模型,采用细网格建模有利于气动结构之间耦合数据的高精度传递。图 5给出了无人机前5阶结构模态特性。
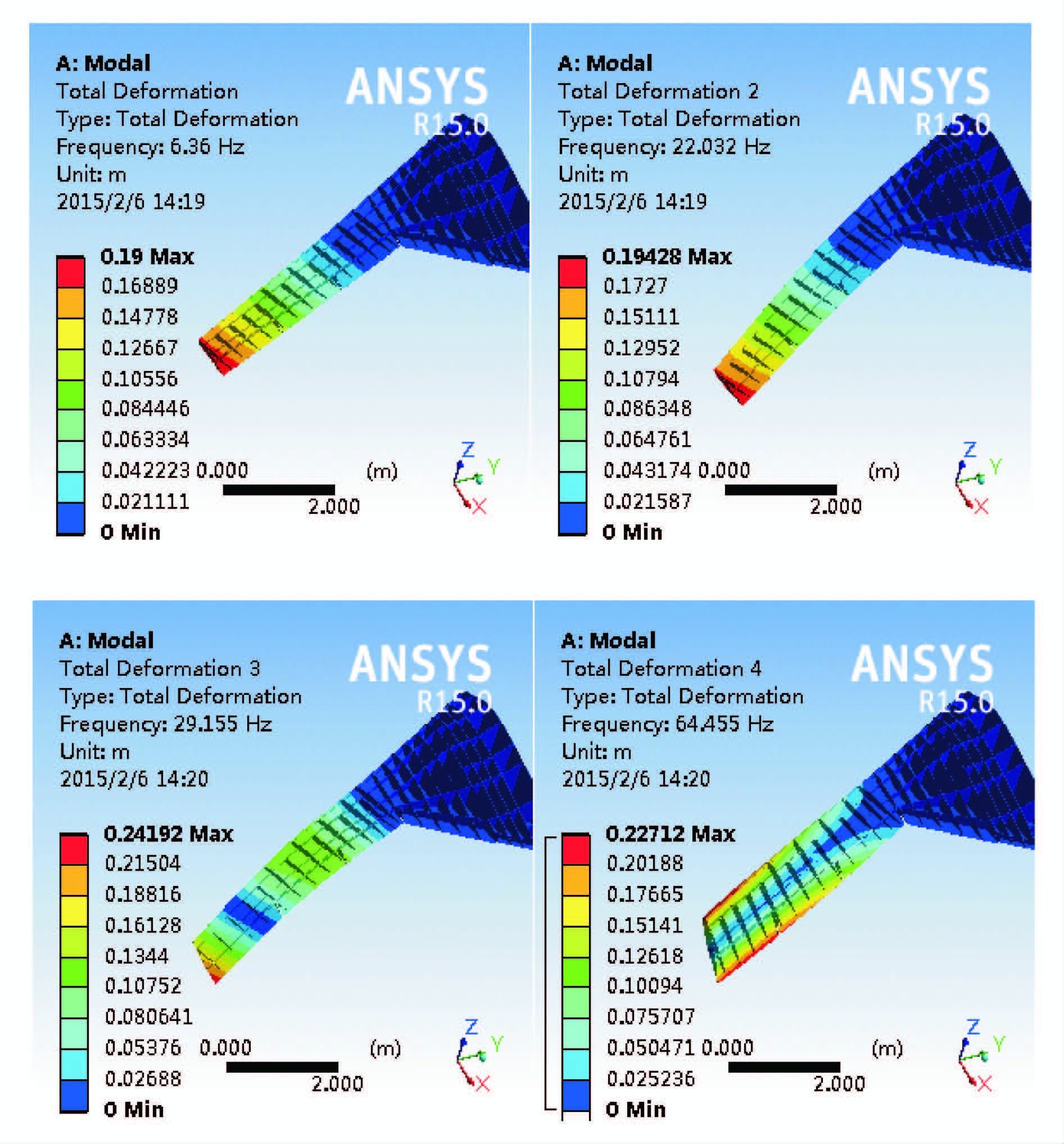
|
图 5 飞翼无人机前4阶模态频率 Figure 5 First four modals of flying-wing UAV |
图 6给出了抖振初始迎角状态下飞翼无人机外翼前缘的位移时频响应。图 6(a)给出了抖振初始迎角状态下飞翼无人机外翼前缘的位移时域响应,从图中可看出:刚开始时外翼前缘位移响应的波动比较大,随着时间的增加外翼前缘位移响应波动有减小的趋势;且当t=1.6s时外翼前缘的位移响应幅值增幅较大。图 6(b)给出了抖振初始迎角状态下飞翼无人机外翼前缘位移响应的频谱分析,从图中的幅值频率曲线中可看出在频率f=7.002Hz处首先出现明显峰值,这与飞翼无人机的一阶模态频率比较接近;且在频率f=28.51Hz处出现第二次峰值,在频率f=62.52Hz处又一次出现峰值。
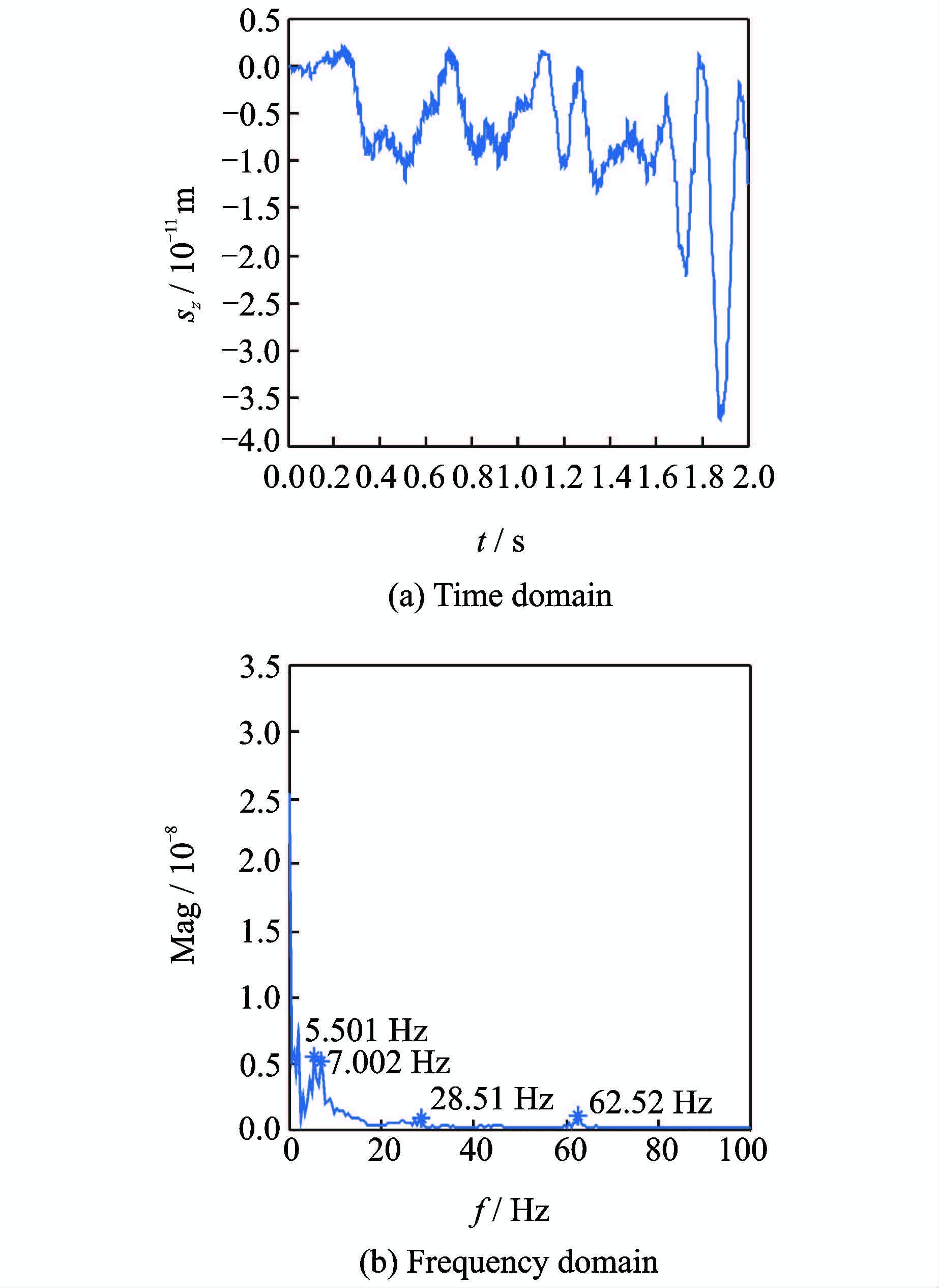
|
图 6 抖振初始迎角下外翼前缘位移响应 Figure 6 Outside wing displacement responses at buffeting onset angle |
图 7给出了抖振初始迎角状态下飞翼无人机外翼前缘的加速度时频响应。图 7(a)给出了抖振初始迎角状态下飞翼无人机外翼前缘的加速度的时域响应,从图中可看出:不同时刻状态下外翼前缘的加速度响应波动比较明显;且当t=1.8 s时外翼前缘的加速度响应波动有所减小。图 7(b)给出了抖振初始迎角状态下飞翼无人机外翼前缘加速度响应的频谱分析,从图中幅值频率曲线中可看出在频率f=7.002Hz处首先出现明显峰值,这与飞翼无人机的一阶模态频率比较接近;且在频率f=28.51Hz处出现第二次峰值,在频率f=62.52Hz处又一次出现峰值。
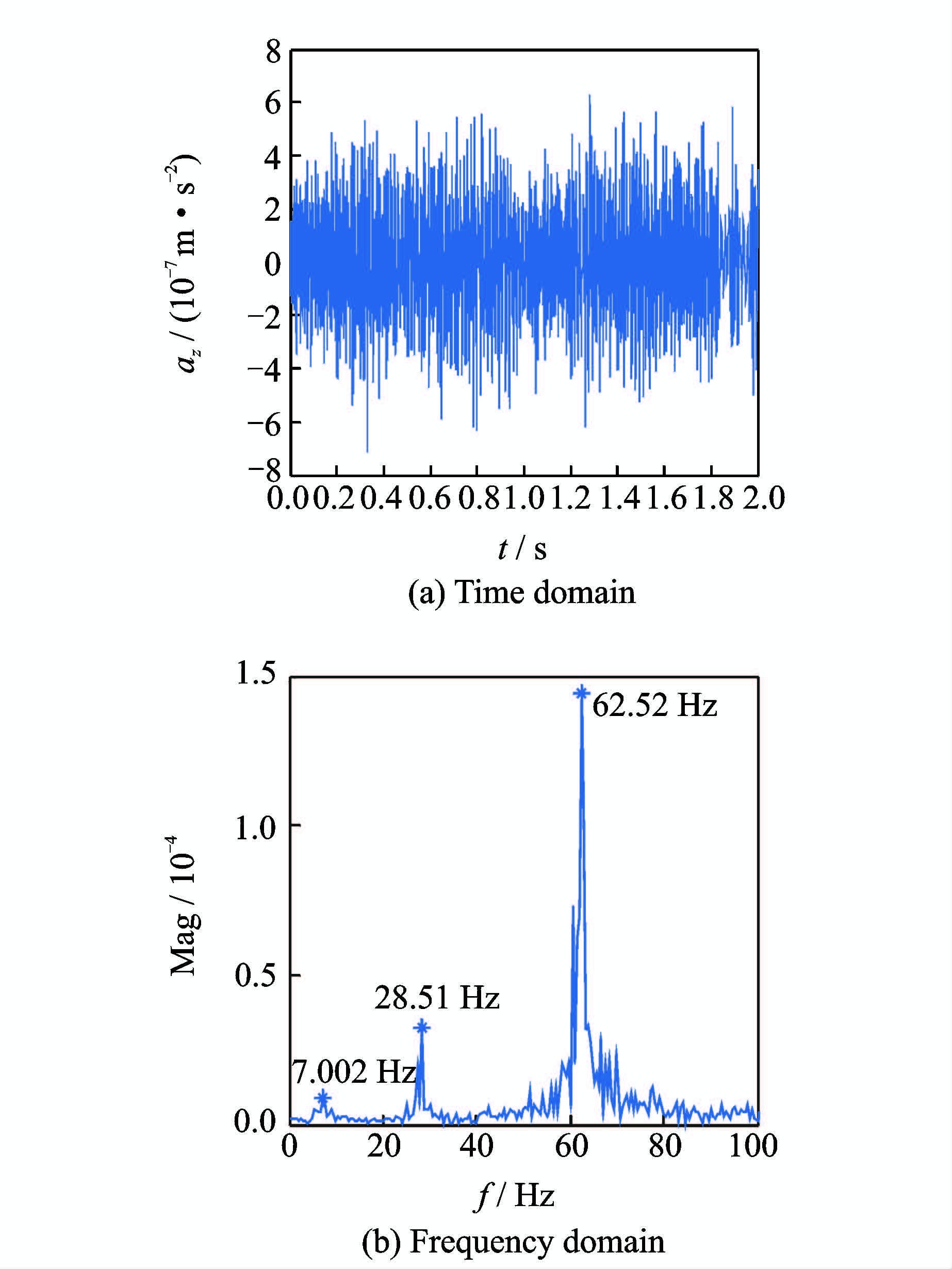
|
图 7 抖振初始迎角下外翼前缘加速度响应 Figure 7 Outside wing acceleration responses at buffeting onset angle |
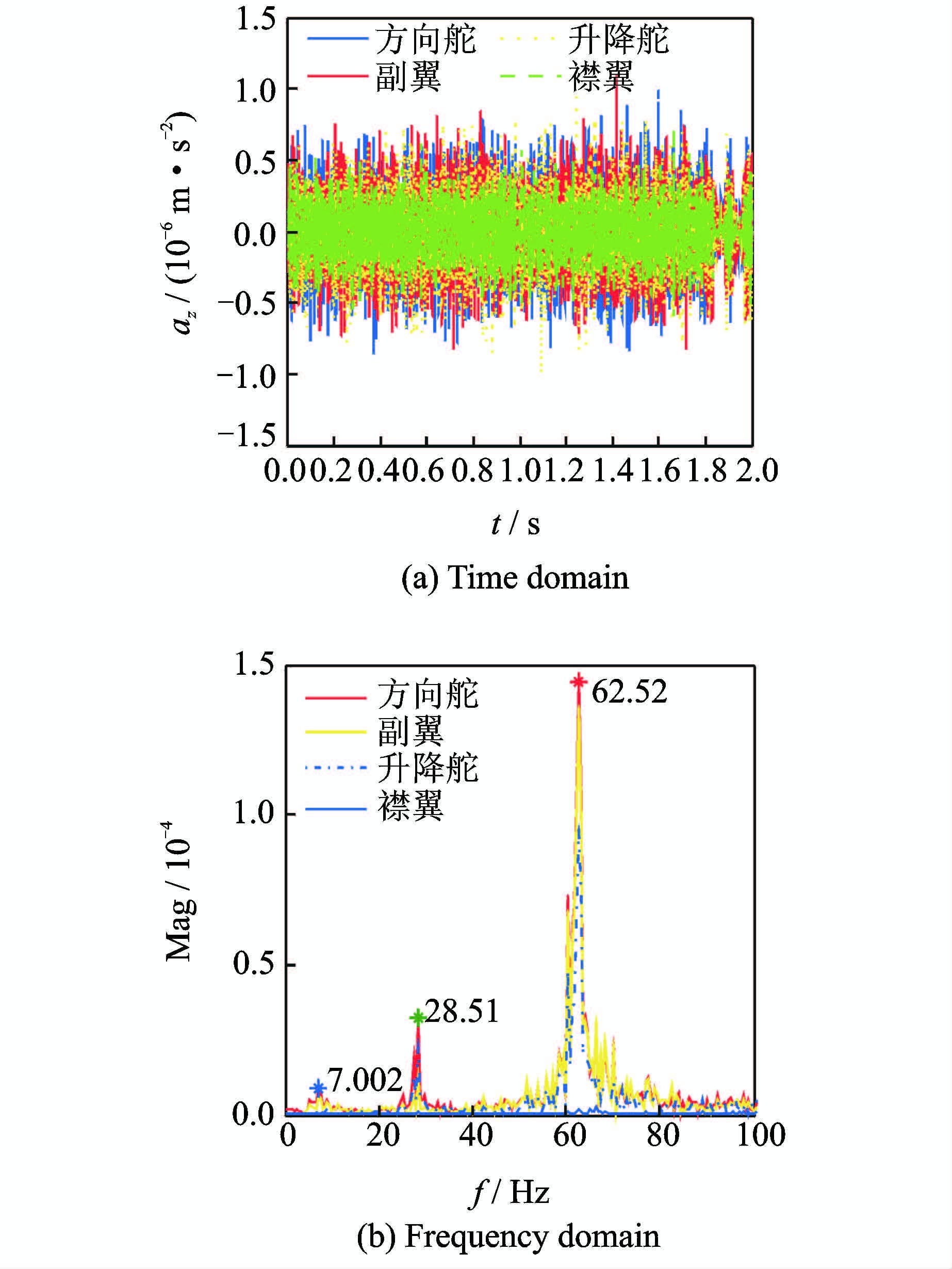
图 8给出了抖振初始迎角状态下飞翼无人机不同舵面的位移时频响应。图 8(a)给出了抖振初始迎角状态下飞翼无人机不同舵面的位移时域响应,从图中可看出:与其他舵面如副翼、升降舵及襟翼相比,方向舵和副翼的位移响应幅值最大,而襟翼和升降舵的位移响应幅值最小。图 8(b)给出了抖振初始迎角状态下不同舵面位移的频率分析。从图中的幅频曲线中可看出不同舵面位置如方向舵、副翼、升降舵及襟翼的频谱响应曲线仅仅是幅值上的差别,舵面不同位置对位移响应的频率并没有影响,因此也可以通过分析方向舵舵面的位移频率特性来研究其他副翼、升降舵及襟翼的位移响应频率特性。在频率f=7.002Hz处方向舵位移响应出现明显峰值,而此频率值与飞翼无人机结构模型的一阶结构模态频率比较接近;副翼和升降舵的明显峰值也可以通过位移频率分析看出,而襟翼的峰值不明显,主要是因为襟翼与其他方向舵、副翼及升降舵相比位移的幅值比较小。
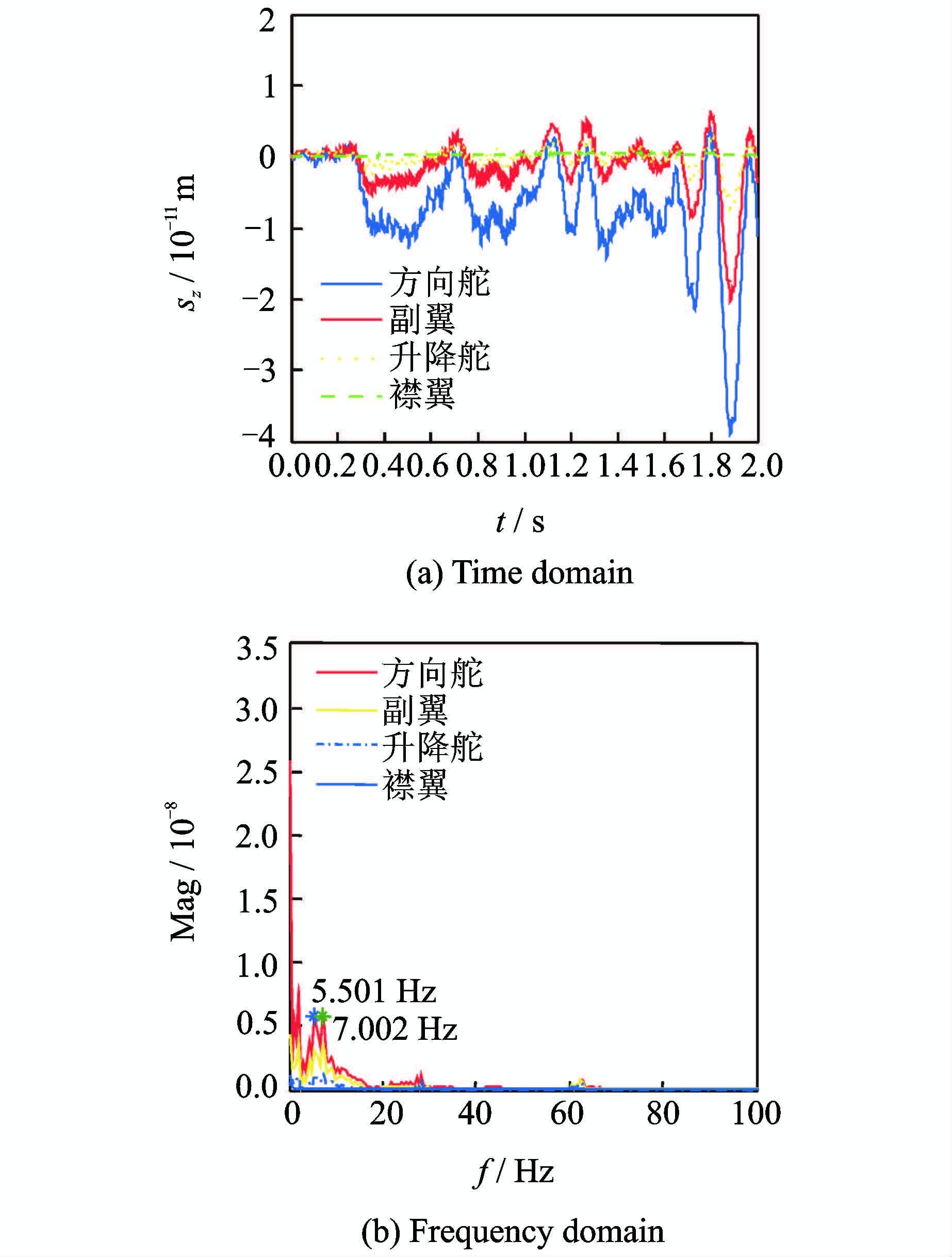
|
图 8 抖振初始迎角下不同舵面位移响应 Figure 8 Different rudder displacement responses at buffeting onset angle |
图 9给出了抖振初始迎角状态下飞翼无人机不同舵面的加速度时频响应。图 9(a)给出了抖振初始迎角状态下飞翼无人机不同舵面的加速度响应,从图中可看出:不同时刻状态下不同舵面位置的加速度响应波动比较明显;且当t=1.8s后不同舵面位置的加速度响应波动均减小。图 9(b)给出了抖振初始迎角状态下飞翼无人机不同舵面如方向舵、副翼、升降舵及襟翼的加速度频率分析。从图中的幅频曲线中还可看出,不同舵面位置如方向舵、副翼、升降舵及襟翼的频谱响应曲线仅仅是幅值上的差别,舵面不同位置对加速度响应的频率并没有影响,因此也可以通过分析方向舵舵面的加速度响应频率特性来研究其他的如副翼、升降舵及襟翼的加速度响应频率特性。在频率f=7.002Hz处方向舵加速度响应出现明显峰值;且在频率f=28.51Hz处出现第二次峰值,又在频率f=62.52Hz处出现较为明显的峰值;副翼的明显峰值也可以通过加速度响应频率分析图看出,而襟翼和升降舵的峰值不明显,主要是因为襟翼与其他的如方向舵、副翼及升降舵相比加速度响应的幅值比较小。
|
图 9 抖振初始迎角下不同舵面加速度响应 Figure 9 Different rudder acceleration responses at buffeting onset angle |
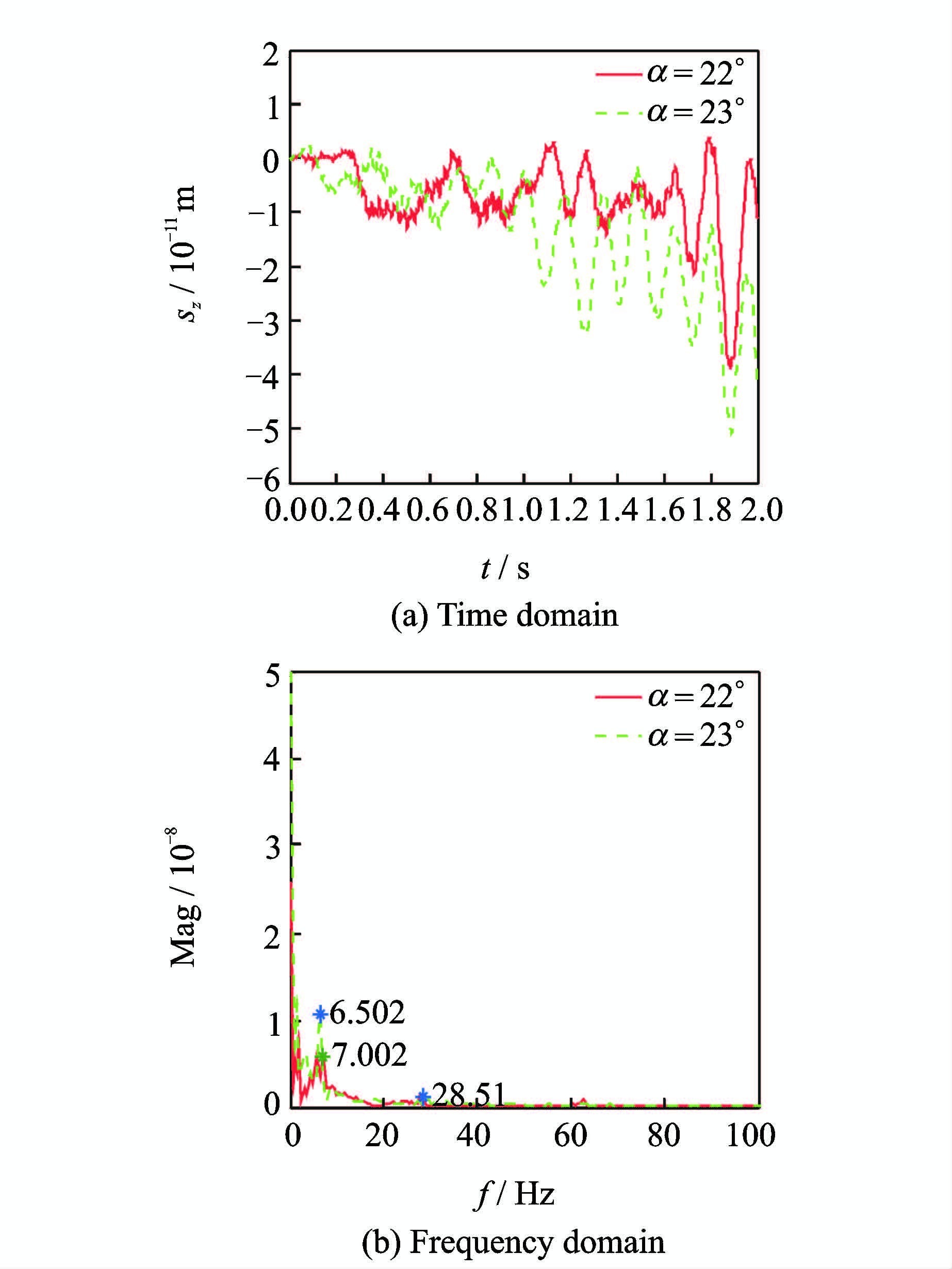
图 10给出了抖振状态下不同迎角下的方向舵位移时频响应。图 10(a)给出了抖振状态下不同迎角下的方向舵位移时域响应历程,从图中可看出:刚开始时方向舵位移响应的波动比较大且波动位移幅值比较小,随着时间的增加位移响应波动有减小的趋势但是响应增大。图 10(b)为抖振状态下不同迎角下的方向舵位移的频谱分析。从图中可看出:方向舵位移响应的频率峰值主要集中于6.502 Hz。
|
图 10 不同迎角下方向舵位移响应 Figure 10 Rudder displacement responses at different angles |
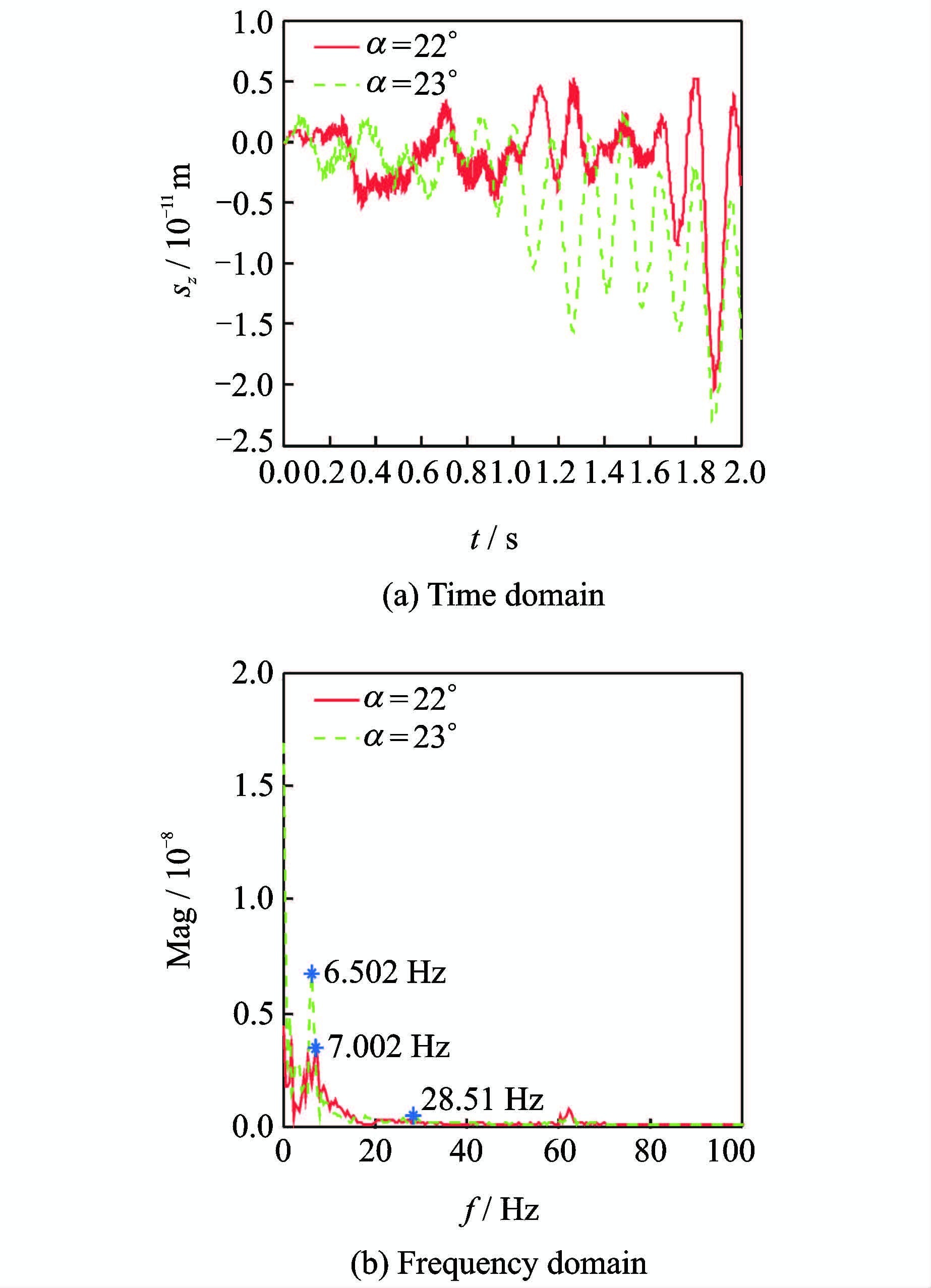
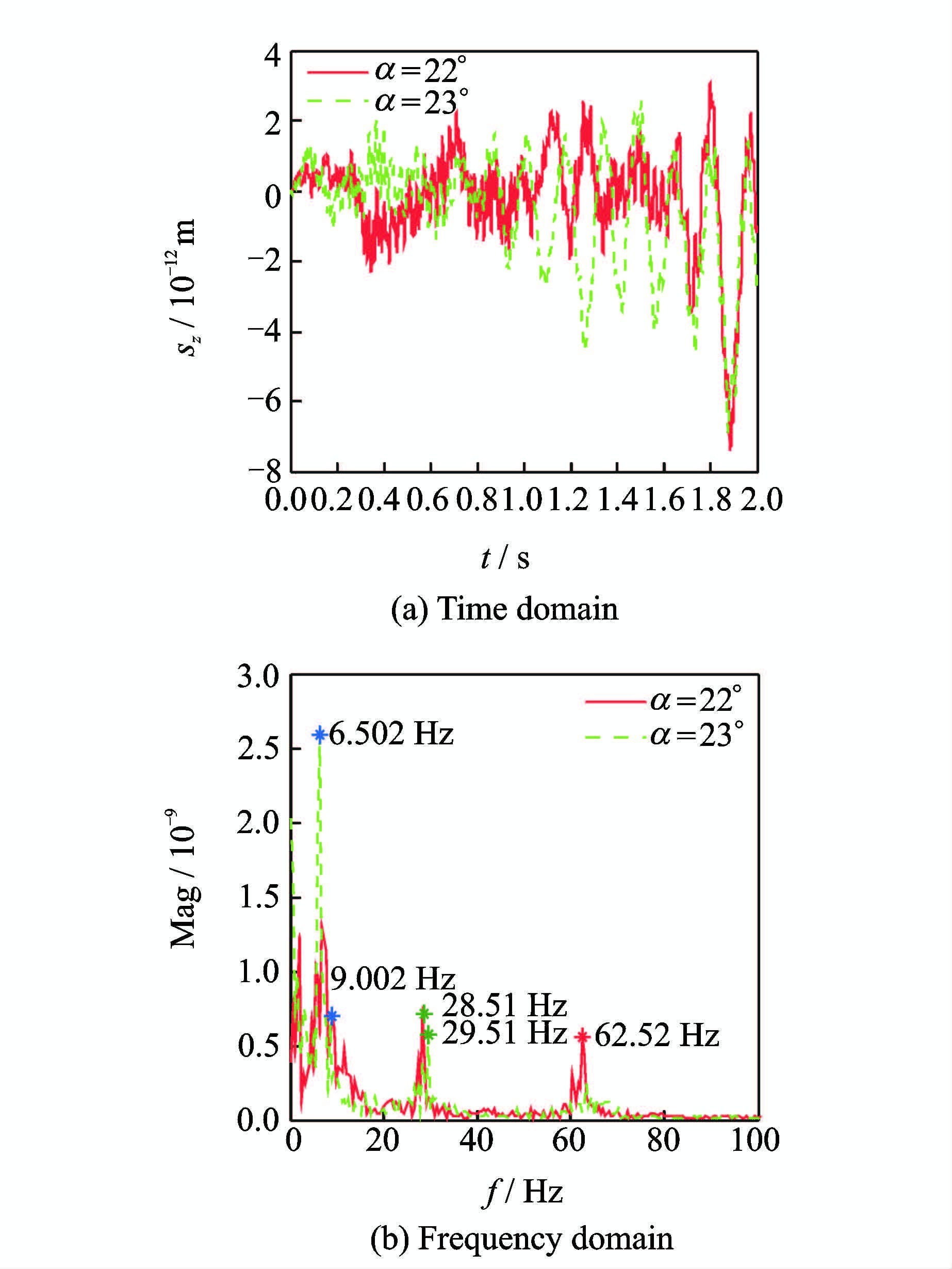
图 11~13分别给出了抖振状态下不同迎角下的副翼、升降舵及襟翼位移时频响应。
|
图 11 不同迎角下副翼位移响应 Figure 11 Aileron displacement responses at different angles |
|
图 12 不同迎角下升降舵位移响应 Figure 12 Elevator displacement responses at different angles |
|
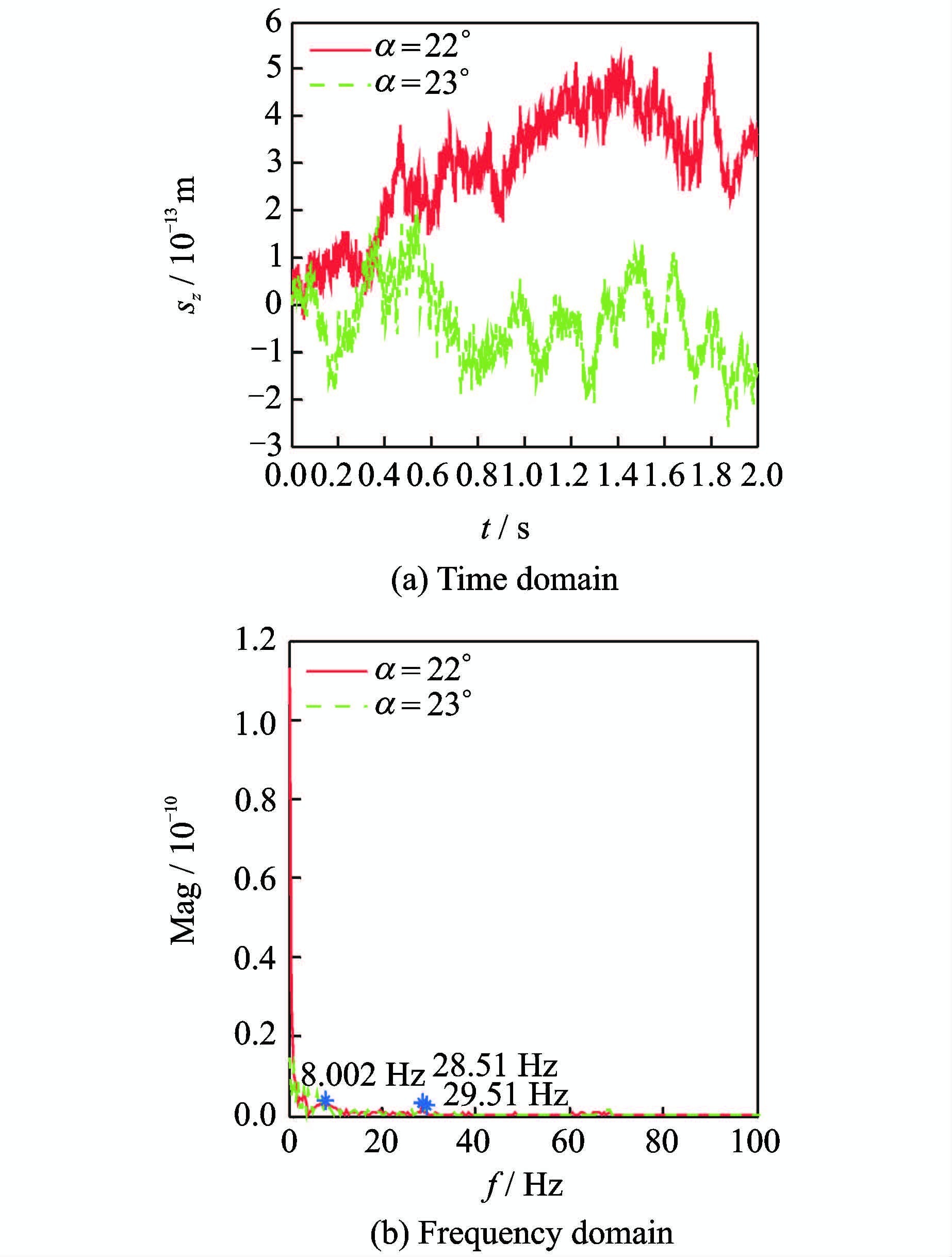
图 13 不同迎角下襟翼位移响应 Figure 13 Flap displacement responses at different angles |
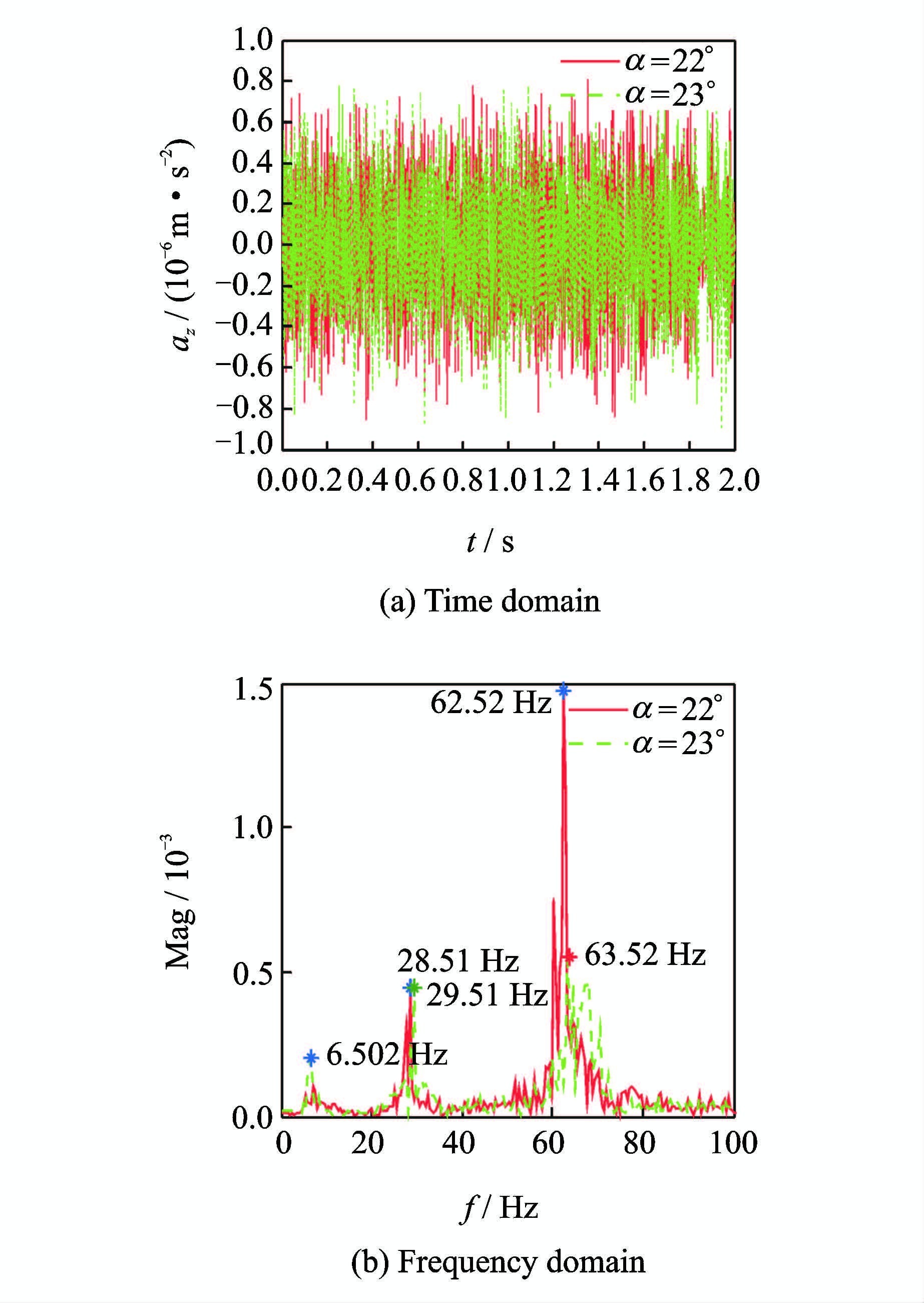
图 14给出了抖振状态下不同迎角下方向舵的加速度时频响应。图 14(a)给出了抖振状态下不同迎角下方向舵的加速度响应。图 14(b)为抖振状态下不同迎角下的方向舵加速度的频谱分析。从图中可看出:升降舵加速度响应的频率峰值首次出现在6.502 Hz,第二次波峰出现在28.51 Hz,又在频率62.52 Hz出现峰值。
|
图 14 不同迎角下方向舵加速度响应 Figure 14 Rudders acceleration responses at different angles |
图 15~17分别给出了抖振状态下不同迎角下的副翼、升降舵及襟翼的加速度时频响应。
|
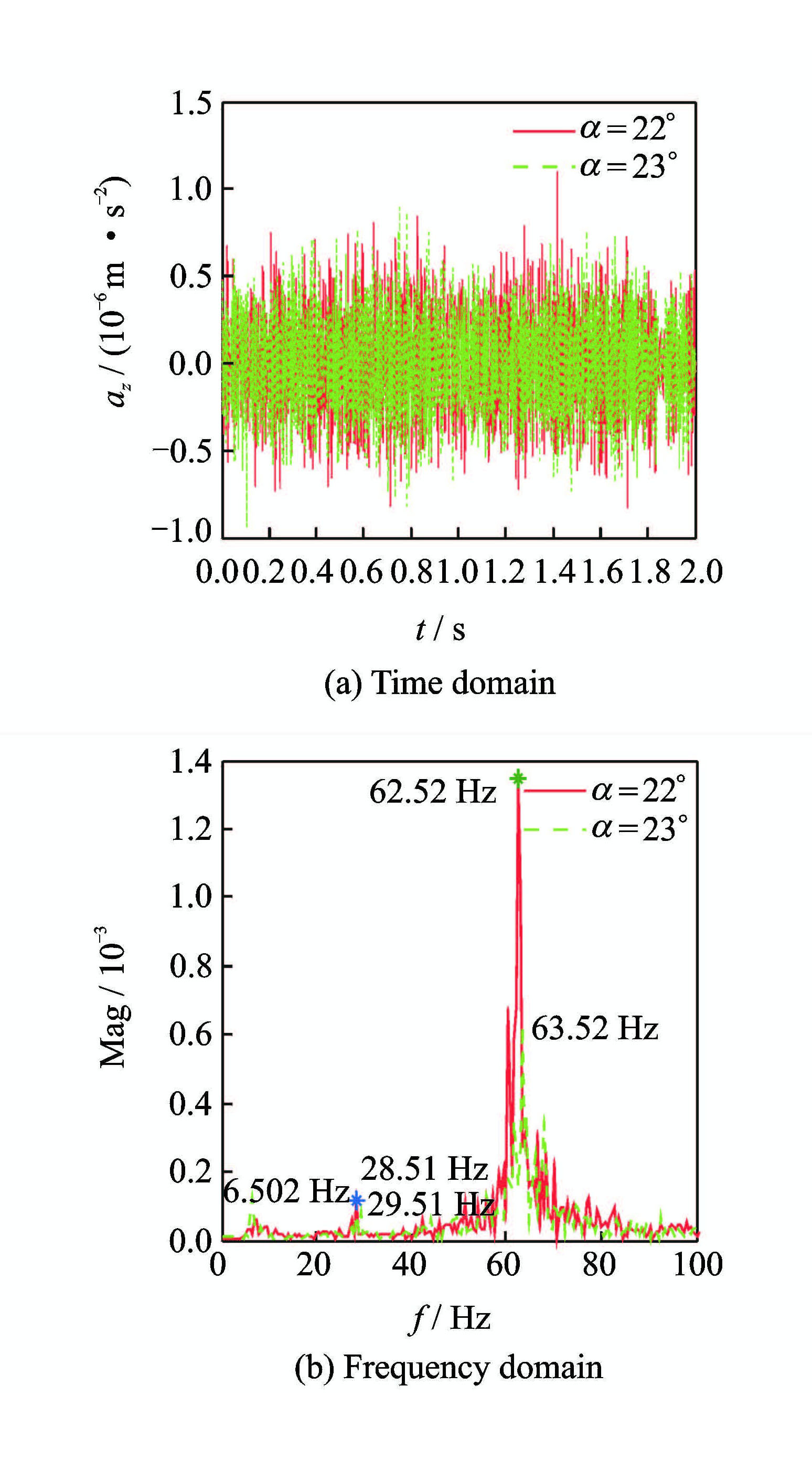
图 15 不同迎角下副翼加速度响应 Figure 15 Aileron acceleration responses at different angles |
|
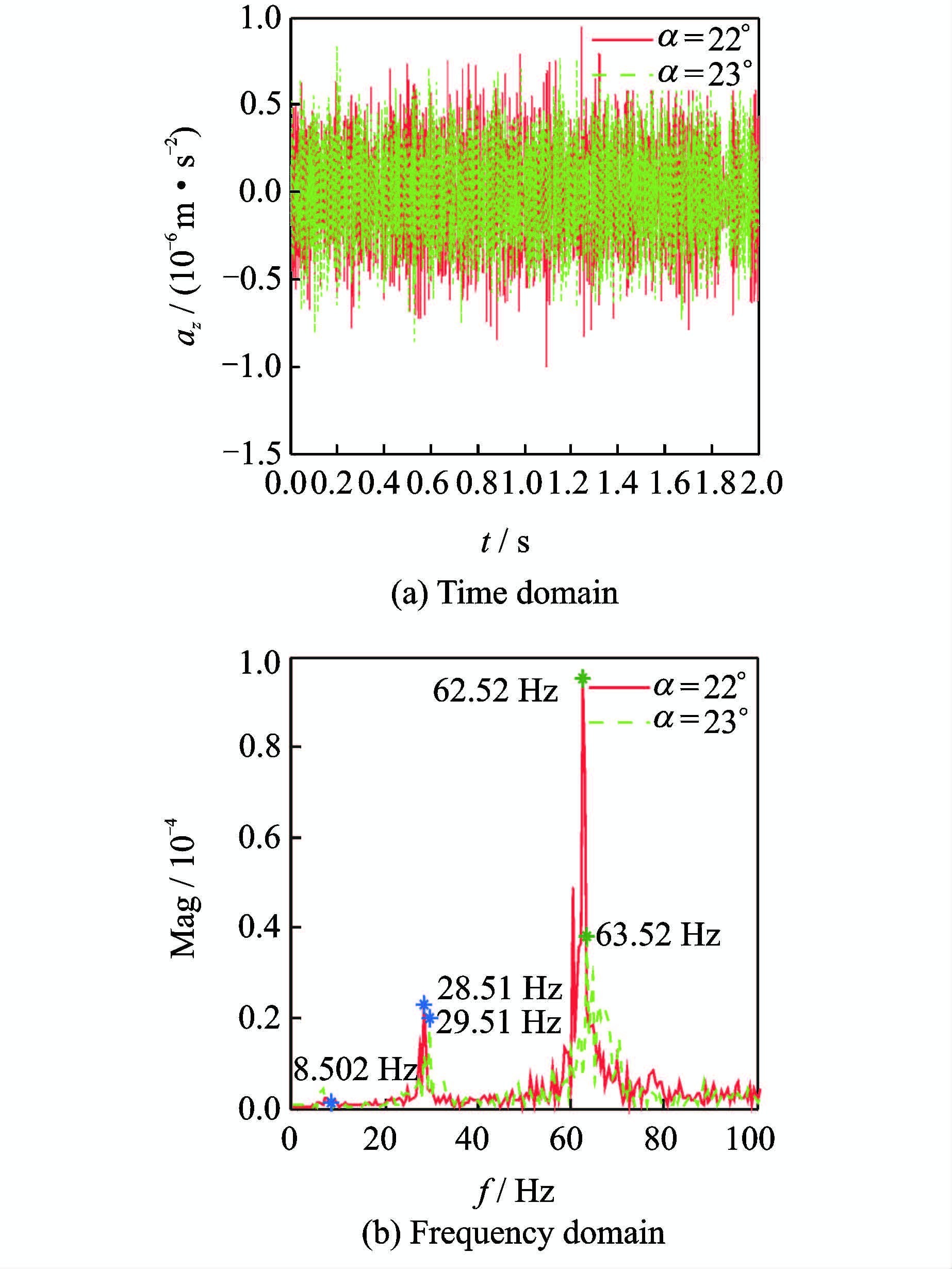
图 16 不同迎角下升降舵加速度响应 Figure 16 Elevator acceleration responses at different angles |
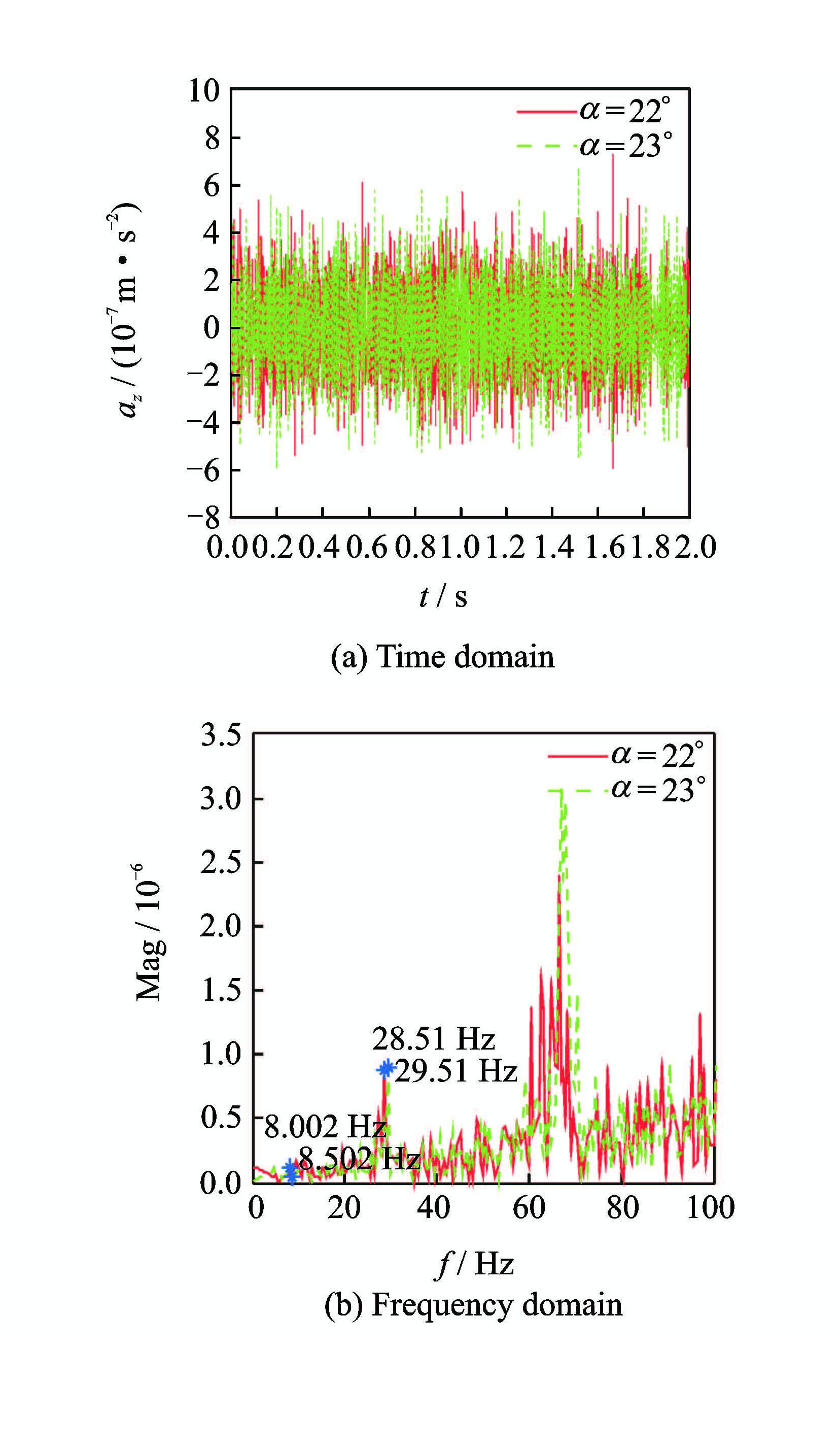
|
图 17 不同迎角下襟翼加速度响应 Figure 17 Flap acceleration responses at different angles |
4 结论
基于RANS方程和SST湍流模型采用飞翼无人机升力系数判据、俯仰力矩判据和表面极限流判据等对刚性飞翼布局无人机在低速大迎角状态下的抖振始发迎角度进行了预测估计,得出此低速状态下的抖振始发迎角为α=22°;对抖振始发迎角附近的抖振载荷进行了气动结构耦合计算;分别在时频域内分析飞翼无人机的抖振载荷响应,主要研究结论如下:
(1) 采用升力系数判据、俯仰力矩系数判据预测的抖振始发迎角与表面极限流判据预测的始发迎角相比要保守一些。
(2) 表面极限流判据预测方法却能给出翼面气流流动的细节,采用此判据可以分析对比不同迎角下的翼面气流流动变化情况。
(3) 与气动弹性及嗡鸣响应相比,抖振是一种强迫振动,其响应频率并不是单一的。
| [1] |
郭同庆, 董璐, 陆志良.
跨音速机翼抖振初始迎角N-S 方程定常计算分析[J]. 航空学报 , 2008, 29 (4) : 810–844.
Guo Tongqing, Dong Lu, Lu Zhiliang. Numerical analysis of buff et onset angle for transonic wing with N-S equations[J]. Acta Aeronautica et As tronautica Sinica , 2008, 29 (4) : 810–844. |
| [2] |
吕志咏, 张明禄, 高杰.
双立尾/三角翼布局的立尾抖振研究[J]. 实验流体力学 , 2006, 20 (1) : 13–16.
Lü Zhiyong, Zhang Minglu, Gao Jie. Study on vertical tail bu ffeting of configuration with twin vertical tails/delta wing[J]. Journal of Ex periments in Fluid Mechanics , 2006, 20 (1) : 13–16. |
| [3] |
黄江涛, 高正红.
应用MDDES的飞行器气动/结构耦合抖振数值模拟[J]. 中国科学 , 2013, 43 (10) : 1071–1080.
Huang Jiangtao, Gao Zhenghong. Buffeting numerical simulation coup led with aerodynami cs and structure based on MDDES[J]. Sci China Tech Sci , 2013, 43 (10) : 1071–1080. |
| [4] |
韩冰, 徐敏, 蔡天星, 等.
涡破裂诱导的垂尾抖振数值模拟[J]. 航空学报 , 2012, 33 (5) : 788–795.
Han Bing, Xu Min, Cai Tianxing, et al. Numerical simulation of ver tical tail buffetin g induced by vortex breakdown[J]. Acta Aeronautica et Astronautica Sinica , 2012, 33 (5) : 788–795. |
| [5] |
李劲杰, 杨青, 肖春生, 等.
边条翼布局流场及其双垂尾抖振特性研究[J]. 航空 学报 , 2006, 27 (3) : 395–398.
Li Jinjie, Yang Qing, Xiao Chunsheng, et al. Investigation of flo w and twin-vertical tail buffet characteristics of leading-edge extension conf iguration[J]. Acta Aeronautica et Astronautica Sinica , 2006, 27 (3) : 395–398. |
| [6] | Kandil O A, Massey S J, Kandil H A. Computations of vortex-breakdown indu ced tail buffet undergoing bending and torsional vibrations[R]. AIAA Paper 199 4-14 28, 1994. |
| [7] | Kandil O A, Sheta E F, Massey S J. Buffet responses of a vertical tai l in vortex breakdown flows[R]. AIAA Paper 1995-3464, 1995. |
| [8] | Kandil O A, Sheta E F, Massy S J. Fluid/structure twin tail buffet re sponse over a wide range of angle of attack[R]. AIAA Paper 1997-2261, 1997. |
| [9] | Morton S A, Cummings R M, Kholodar D B. High resolution turbulence tr eatm ent of F/A-18 tail buffet[J]. Journal of Aircraft , 2007, 44 (6) : 1769–1775. DOI:10.2514/1.29577 |
| [10] | Healey M D. F/A-18 E/F vertical tail buffet design, anal ysis and test[R]. AIAA Paper 2003-1886, 2003. |
| [11] | Steimle P C, Schroder W, Klaas M. Transonic shock buffet i nterferenc e of an oscillating high aspect ratio swept wing[J]. AIAA Paper 2008-6908, 20 08. |
| [12] | Xu Jun, Ma Xiaoping. Transonic rudder buzz on tailless flying wing UAV[J]. Transactions of Nanjing University of Aeronautics & Astron autics , 2015, 32 (1) : 61–69. |
| [13] |
许军, 马晓平.
飞翼无人机嗡鸣气动弹性响应分析[J]. 西北工 业大学学报 , 2015, 33 (4) : 588–595.
Xu Jun, Ma Xiaoping. Buzz aeroelastic responses analysis for a fly ing wing UAV[J]. Journal of Northwestern Polytechnical University , 2015, 33 (4) : 588–595. |
| [14] |
孟令兵, 昂海松, 肖天航.
柔性翼微型飞行器流固耦合数值模拟[J]. 南京航空航天大学报 , 2013, 45 (5) : 621–627.
Meng Lingbing, Ang Haisong, Xiao Tianhang. Numerical sim ulation of fluid-structure interaction for flexible wing MAV[J]. Journal of Nanjing Uni versity of Aeronautics & Astronautics , 2013, 45 (5) : 621–627. |
 2016, Vol. 48
2016, Vol. 48


