受前行桨叶激波和后行桨叶气流分离的影响[1],常规构型直升机的最大平飞速度被限制在300 km/h左右。以Sikorsky X2为代表的高速直升机(图 1),采用共轴刚性旋翼解决了常规直升机前飞速度偏低的问题[2]。但该类直升机在高速前飞时,由于桨毂构造复杂,将产生较强的气流分离使阻力激增(桨毂阻力占全机阻力的50%)[3]。而加装流线形的整流罩能有效减小废阻。

|
图 1 X-2共轴刚性旋翼高速直升机 Figure 1 X-2 coaxial-rigid-rotor high-speed helicopter |
早在20世纪70年代,美国就开始了桨毂减阻研究,在桨毂阻力分布、桨毂被动减阻方法和桨毂阻力预测等方面积累了大量经验和数据。文献[4~7]研究了单旋翼直升机桨毂不同整流外形、整流部件间缝隙、主轴塔 座高度以及旋翼轴倾斜等情况对阻力特性的影响。Felker等以全尺寸和1/5缩比的XH-59A机身为模型,研究了共轴双旋翼直升机的桨毂整流罩和旋翼轴整流罩的阻力特性[8]; Young等对比分析了单旋翼和共轴双旋翼直升机桨毂减阻的异同[9];Martin等着力对纵向截面为梯形的主轴塔座进行了研究[10];文献[11~12]在文献[8]的基础上,采用基于非结构网格的流场求解器对不旋转的共轴双桨毂的阻力进行了研究并发展了相应的评估软件。中国国内,曾伟等人对共轴刚性旋翼直升机不同的桨毂和连接轴构型进行了建模计算[13]。
出于简化计算模型和试验方法的考虑,上述研究大都是将桨毂整流罩、旋翼轴和主轴塔座等部件作为一个连续的整体模型来处理,忽略了共轴双桨毂的旋转运动以及旋转部件与静止部件之间缝隙的影响。因此,本文以典型布局的共轴桨毂整流装置模型为研究对象,采用风洞试验手段,研究了旋转运动、各部件间缝隙以及不同外形布局对桨毂整流装置的阻力和表面流动特性的影响规律,初步揭示了无旋翼下洗流时影响共轴桨毂整流装置阻力的因素。
1 试验设备与方法试验在中国空气动力研究与发展中心的1.4 m×1.4 m风洞中进行,模型安装在自研的共轴双桨毂模型试验台上,阻力由TH1001B盒式天平测量,试验风速为18~32 m/s,Re=0.38×106~0.68×106。
1.1 风洞1.4 m×1.4 m风洞是一座直流闭口试验段低速风洞,试验段长2.8 m;试验段中心截面有效面积为1.88 m2。风洞最高稳定风速可达50 m/s,最低稳定风速为10 m/s,流场品质达到相关标准要求。
1.2 共轴双桨毂模型试验台共轴双桨毂模型试验台主要由电机、锥齿轮、内轴、外轴、轴承座以及天平等组成。上桨毂整流罩和下桨毂整流罩由3个锥齿轮驱动,实现共轴反转。风挡安装在风洞地板上,试验现场如图 2所示。

|
图 2 安装于风洞中的试验模型 Figure 2 Test model fixed in wind tunnel |
1.3 试验模型
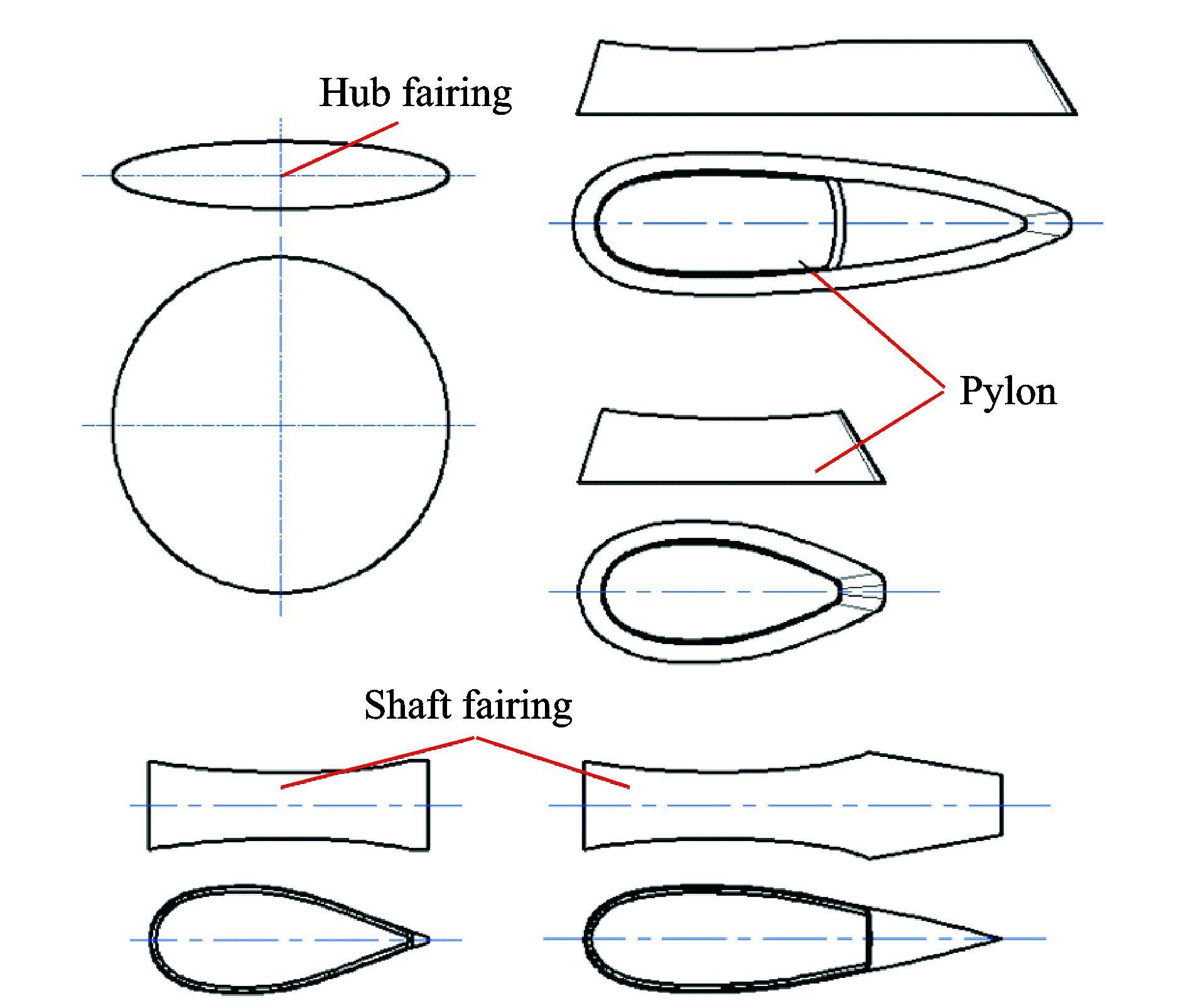
试验模型包括一种桨毂整流罩、两种中间轴整流罩和两种主轴塔座,外形如图 3所示。桨毂整流罩为回转体,横截面为椭圆,椭圆长轴半径为170 mm、短轴半径为34 mm;上、下桨毂中心距离为136 mm;中间轴整流罩长度分别为422,282 mm,最低点高度均为67 mm;主轴塔座长度分别为500,310 mm,最低点高度均为67 mm。
|
图 3 整流罩模型 Figure 3 Fairing configurations |
本文共对6种模型组合进行了试验,包括仅短塔座(组合A)、短中间轴整流罩与短塔座(组合B)、长中间轴整流罩与短塔座(组合C)、仅长塔座(组合D)、短中间轴整流罩与长塔座(组合E)以及长中间轴整流罩与长塔座(组合F),如图 4所示。

|
图 4 试验模型组合 Figure 4 Test model groups |
1.4 试验数据处理方法
将6种模型组合的阻力数据处理成阻力面积CxS的形式,用以衡量不同模型组合所受阻力大小,阻力面积定义:阻力与动压之比,公式如下
| ${{C}_{x}}S=\frac{D}{\frac{1}{2}\rho {{V}^{2}}}=\frac{DRT}{\frac{1}{2}P{{V}^{2}}}$ | (1) |
式中:D为阻力;ρ为空气密度;V为风速;P为空气压强;T为洞内温度;R为气体常数。
试验阻塞度为6.5%,模型中心距风洞地板高度约0.7 m,处于风洞试验段中心流场处。试验数据未进行修正。
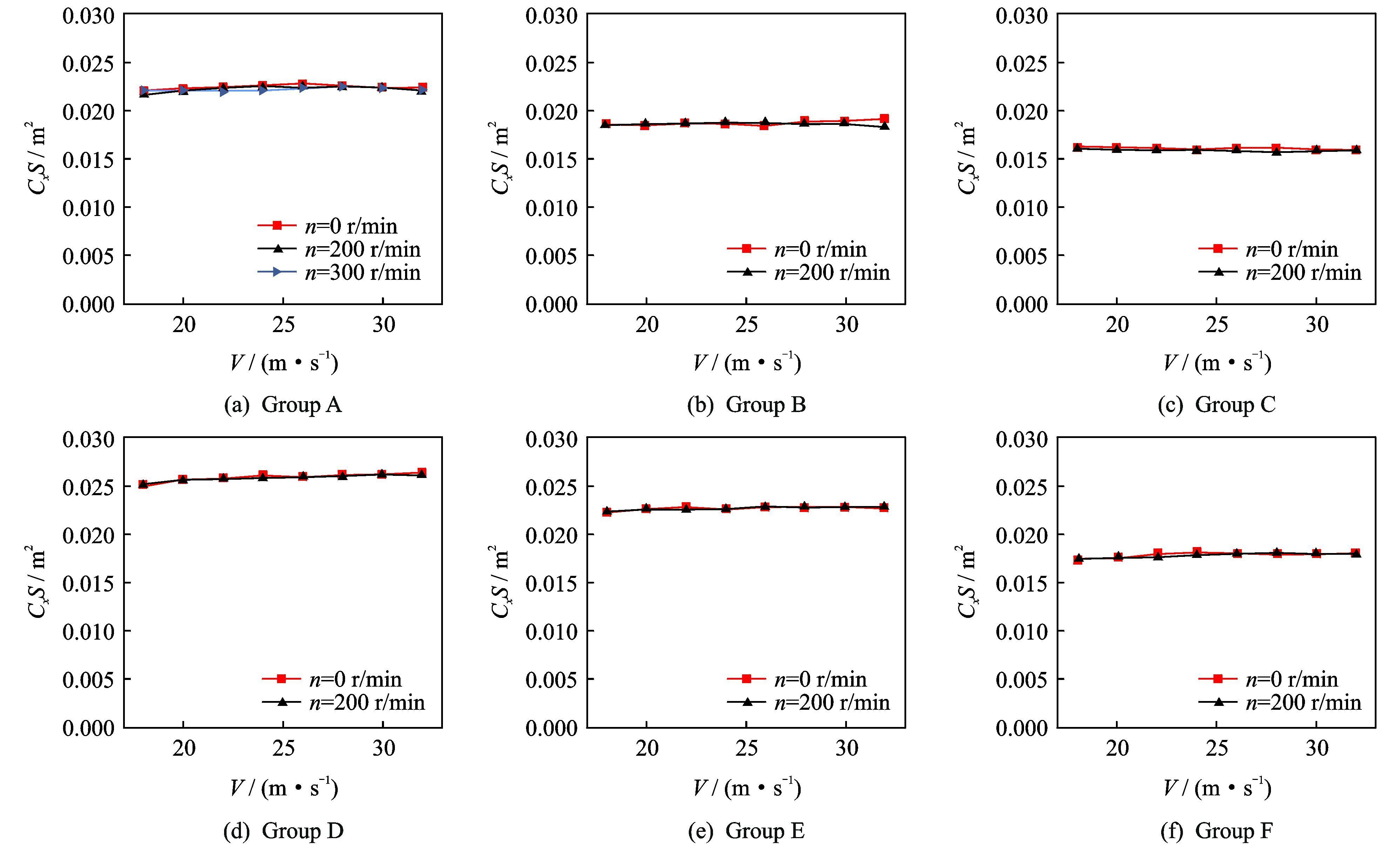
2 结果与分析 2.1 桨毂旋转运动对阻力特性的影响为了得到桨毂旋转运动对整流装置阻力特性的影响规律,将不同模型组合在不同旋转速度下的阻力面积进行对比分析。图 5(a)给出了上下桨毂在n=0,200,300 r/min转速时组合A的阻力面积变化曲线。由图可以看出,桨毂旋转与不旋转时组合A的阻力面积基本不变;图 5(b~f)所示为组合B~F时,上下桨毂在n=0,200 r/min转速时模型的阻力面积,由图同样可以看出模型所产生的阻力受桨毂旋转的影响很小。究其原因,本文所使用的桨毂整流罩是一个轴对称的光滑圆盘,旋转运动对其流场产生的影响较小,所以同一个模型组合在不同的旋转运动下测量得到的阻力几乎相同。因此,在低速条件下研究类似对称光滑桨毂模型阻力特性时,可以不考虑桨毂旋转运动的影响,这对于简化试验装置、提高试验效率和优化设计效率有较大益处。
|
图 5 桨毂不同转速时产生的阻力面积 Figure 5 Drag area of hub at different rotation speeds |
2.2 缝隙对阻力特性的影响
为了研究缝隙大小对整流装置阻力特性的影响,将组合F在不同缝隙大小时的阻力面积进行对比(如图 6,上桨毂与中间轴整流罩和下桨毂与中间轴整流罩之间的缝隙为缝隙1,下桨毂整流罩与主轴塔座之间的缝隙为缝隙2)。

|
图 6 两处缝隙 Figure 6 Two gaps |
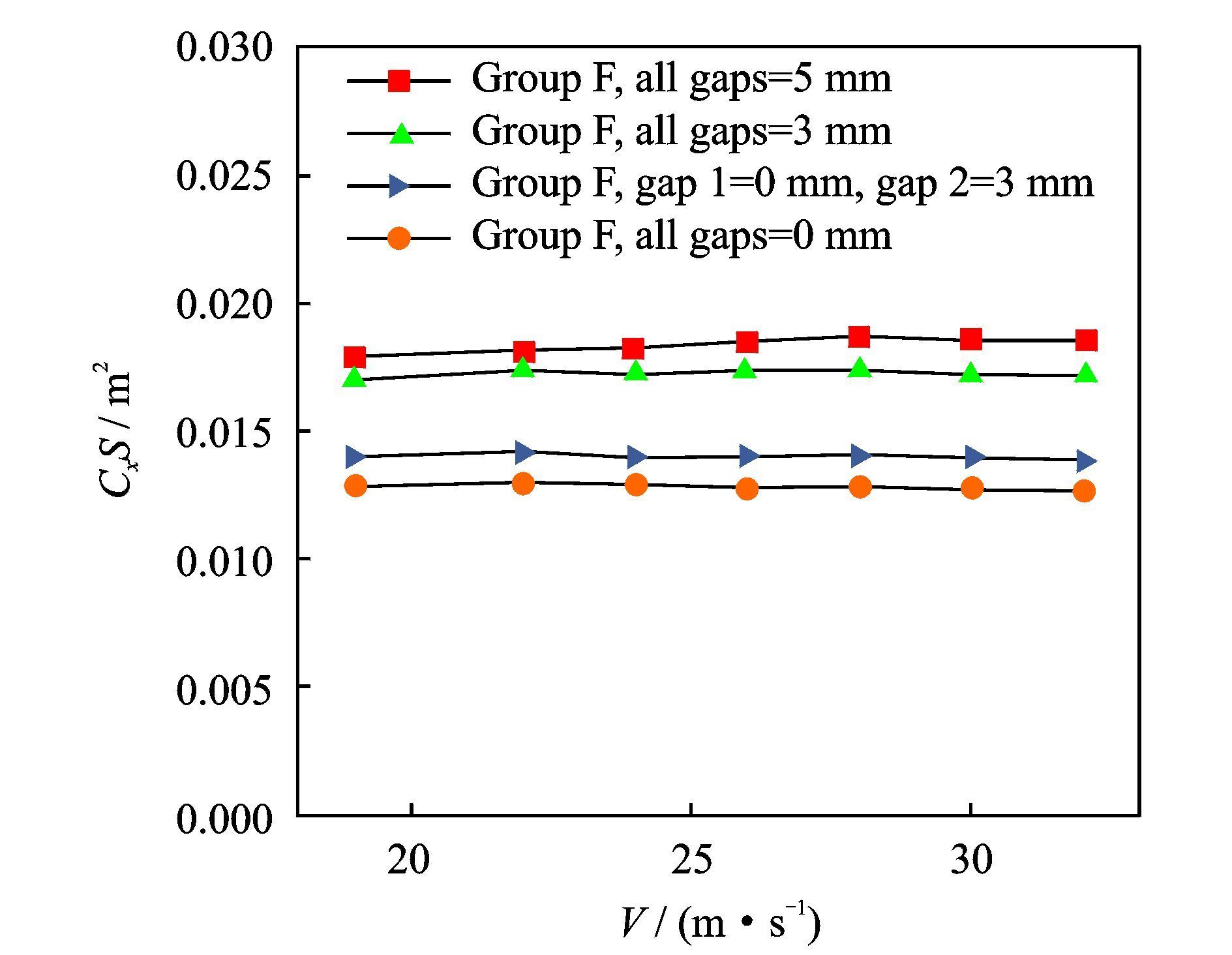
缝隙对阻力面积的影响如图 7所示。由图 7可以看出,所有缝隙为5 mm时,阻力面积最大,为0.018 m2;而将所有缝隙调至3 mm时,阻力面积有所减小,为0.017 m2;当缝隙1=0 mm、缝隙2=3 mm时, 阻力面积大幅下降,为0.014 m2;而当缝隙1和缝隙2密封时,阻力面积降至最低,为0.013 m2,较缝隙1=0 mm、缝隙2=3 mm时减小了7.1%。究其原因,当缝隙较大时,气流由缝隙进入中间轴整流罩和主轴塔座内部,拍打其后部产生附加阻力,且气流通过中间轴后会产生一定的压差阻力。所以,同一模型组合的阻力受缝隙大小的影响较大,为充分发挥中间轴整流罩和主轴塔座的整流减阻作用,应尽可能减小缝隙1和缝隙2的宽度。
|
图 7 缝隙对阻力面积的影响 Figure 7 Effect of gap width on drag area |
2.3 外形参数对阻力特性的影响
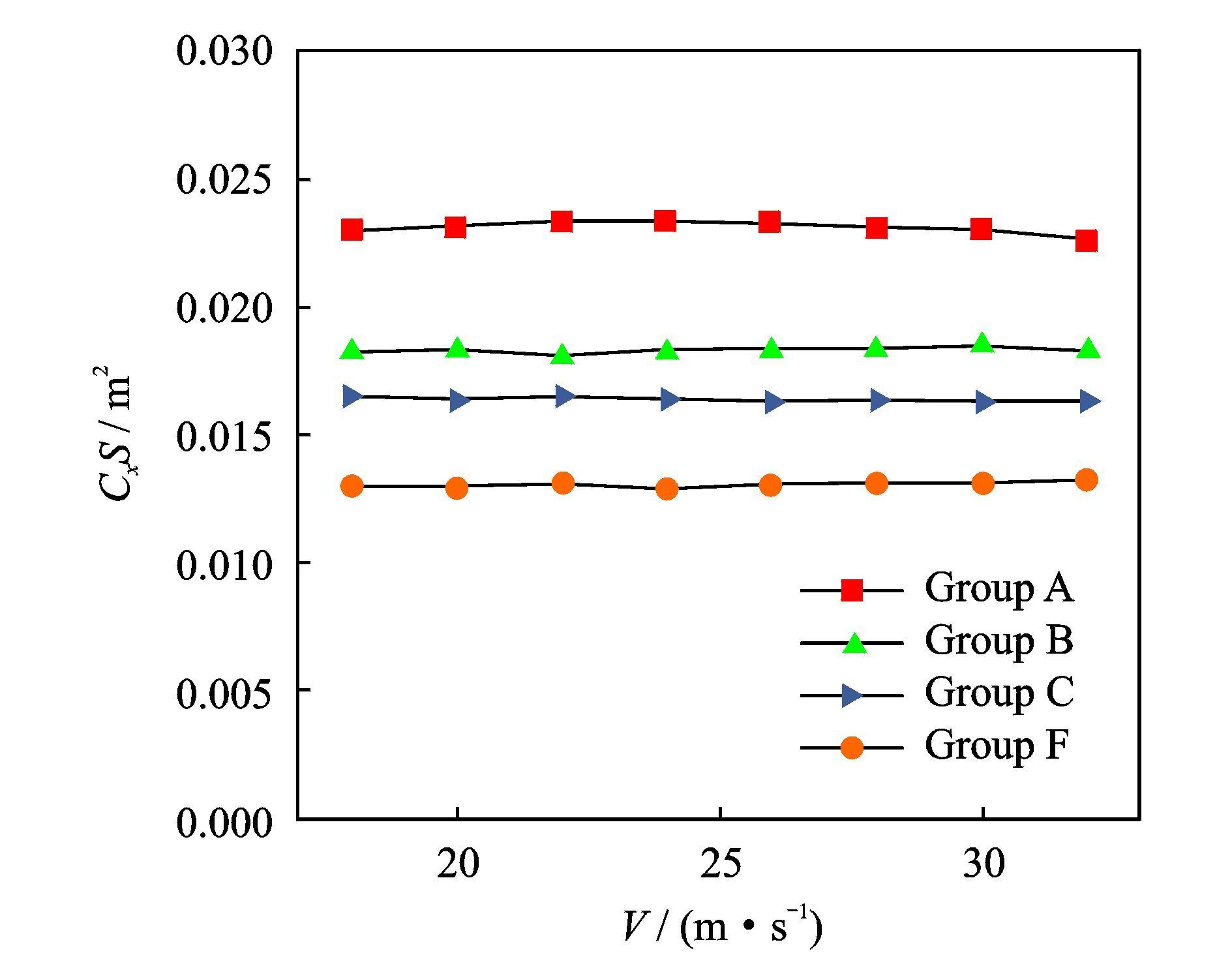
为了研究不同外形参数对阻力特性的影响,将组合A,B,C,F的阻力面积进行对比分析(图 8)。为避免各部件间缝隙对试验数据产生影响,将缝隙1和缝隙2密封。而密封后的桨毂无法旋转,但由2.1节的结论可以知道,桨毂旋转与否对试验结果无实质性影响。
|
图 8 不同模型组合对阻力面积的影响 Figure 8 Effect of different test models on drag area |
不同模型组合对阻力面积的影响如图 8所示。由图 8可以看出每条曲线的变化趋势基本一致,但是不同模型组合在相同风速下的阻力面积大小有明显区别。组合F的阻力面积最小,而组合C,B,A依次增大,分别为0.016,0.018,0.023 m2;组合C,B与组合A相比,阻力面积分别下降30.4%,21.7%,得益于中间轴整流罩的整流作用;而组合C的阻力面积比组合B的小11.1%,说明长中间轴整流罩的整流效果优于短中间轴整流罩。究其原因,试验时组合A的中间轴形成了较强的分离尾流,分离尾流对上下桨毂整流罩有较强的气动干扰,而加装短中间轴整流罩后,能减弱气流的分离,加装长中间轴整流罩能进一步减弱气流分离。
由图 8还可以得出,组合C的阻力面积比组合F的大23.1%,说明长塔座的整流效果优于短塔座的。究其原因,塔座形成的分离尾流对下桨毂整流罩形成气动干扰,且长塔座减弱气动干扰的能力优于短塔座的,故组合F的阻力面积小于组合C的面积。
2.4 表面流动特性为揭示共轴双桨毂整流罩分离尾流干扰对其阻力影响的机理,开展了不旋转状态下共轴桨毂整流装置模型表面流动特征的油流显示试验(风速V=25 m/s),对比了组合B,F构形下各部件表面流动的附着和分离流动特征。图 9为共轴双桨毂油流试验结果,图中红线代表分离线。可以看出,上下桨毂整流罩表面流态差别较大,下桨毂整流罩上表面与上桨毂整流罩上表面相比,下桨毂整流罩上表面有明显的分离区(图 9(a,c)),说明中间轴整流罩的分离尾流对下桨毂整流罩上表面的流场有较强干扰作用,并在下桨毂整流罩后方形成了低压区,增加了桨毂整流罩的阻力;同时,中间轴整流罩在上桨毂整流罩下表面、主轴塔座在下桨毂整流罩下表面均会形成分离区(图 9(b,d)),使阻力增大。由图 9还可以得出,组合B下桨毂的分离区大于组合F下桨毂的分离区;组合F的长中间轴整流罩和塔座的分离线与组合B的相比有所退后,故组合B的阻力面积大于组合F的面积。

|
图 9 桨毂油流试验(风速25 m/s) Figure 9 Oil flow test of hub (V=25 m/s) |
由图 9还可以得出,这两种中间轴整流罩和主轴塔座外形不是最优外形,仍然不能完全抑制中间轴区域以及塔座区域的气流分离,后期可以进一步设计优化中间轴整流罩和主轴塔座的外形。
3 结论综合试验研究结果,可以得出以下结论:
(1) 在低风速条件下,共轴双桨毂试验模型的阻力受对称光滑桨毂旋转运动的影响基本可忽略,这有助于简化试验装置、提高试验效率和优化设计效率;若桨毂为非对称或非光滑,试验时需考虑桨毂旋转运动对阻力的影响。
(2) 试验模型所受阻力对各整流部件间缝隙变化敏感,大缝隙会使试验模型阻力增大。为减小桨毂阻力,应尽量减小各部件间缝隙。
(3) 中间轴整流罩以及主轴塔座的分离尾流对上下桨毂整流罩有较大的气动干扰,这会使模型所受阻力明显增大。
(4) 对共轴双桨毂整流罩来说,适当加长中间轴整流罩和主轴塔座能抑制或推后模型气流分离,减小气动干扰,从而有利于减小模型所产生的阻力。
| [1] | 王适存. 直升机空气动力学[M]. 南京: 航空专业教材编审组, 1985 : 127 -129. |
| [2] |
邓景辉.
高速直升机前行桨叶概念旋翼技术[J]. 航空科学技术 , 2012 (3) : 9–14.
Deng Jinghui. The ABC rotor technology for high speed helicopter[J]. Aeronautical Science & Technology , 2012 (3) : 9–14. |
| [3] |
吴希明.
高速直升机发展现状?趋势与对策[J]. 南京航空航天大学学报 , 2015, 47 (2) : 175–179.
Wu Ximing. Current status, development trend and countermeasure for high-speed rotorcraft[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2015, 47 (2) : 175–179. |
| [4] | Sheehy T W. A general review of helicopter rotor hub drag data[J]. Journal of the American Helicopter Society , 1977, 22 (2) : 2–10. |
| [5] | Sung D Y, Lance M B, Young L A, et al. An experimental investigation of helicopter rotor hub fairing drag characteristics[R]. NASA-TM-102182, 1989. |
| [6] | Logan A H, Prouty R W, Clark D R. Wind tunnel tests of large- and small-scale rotor hubs and pylons[R]. USAAVRADCOM-TR-80-D-21, 1981. |
| [7] | Stroub R H, Young L A, Graham D R, et al. Investigation of generic hub fairing and pylon shapes to reduce hub drag[R]. NASA-TM-100008, 1987. |
| [8] | Felker F F. An experimental investigation of hub drag on the XH-59A[R]. AIAA Paper 85-4065, 1985. |
| [9] | Young L A, Graham D R, Stroub R H. Experimental investigation of rotorcraft hub and shaft fairing drag reduction[J]. J Aircraft , 1987, 24 (12) : 110–123. |
| [10] | Martin D M, Mort R W, Young L A, et al. Experimental investigation of advanced hub and pylon fairing configurations to reduce helicopter drag[R]. NASA-TM-4540, 1993. |
| [11] | Wake B E, Hagen E, Ochs S S, et al. Assessment of helicopter hub drag prediction with an unstructured flow solver[C]// Proceedings of American Helicopter Society 65th Annual Forum. Texas Grapevine, USA: United Technologies Research Center, 2009. |
| [12] | Ochs S S, Matalanis C G, Wake B E. Evaluation of helios CFD toolset for faired rotor-hub drag prediction[C]//Proceedings of American Helicopter Society 67th Annual Forum. Virginia Beach, USA: United Technologies Research Center, 2011. |
| [13] |
曾伟, 林永峰, 黄水林, 等.
共轴双旋翼桨毂减阻初步分析研究[J]. 直升机技术 , 2014 (4) : 14–18.
Zeng Wei, Lin Yongfeng, Huang Shuilin, et al. Preliminary analytical study on drag reduction of coaxial rotors hub[J]. Helicopter Technique , 2014 (4) : 14–18. |
 2016, Vol. 48
2016, Vol. 48


