2. 中国直升机设计研究所,景德镇,333000
2. China Heli copter Research and Development Institute, Jingdezhen, 333000, China
桨/涡干扰(Blade-vortex interaction,BVI)是由旋转的桨叶与各桨尖涡线靠近相遇而形成的一种直升机旋翼所特有的干扰物理现象,当BVI出现时,会伴随着强烈的BVI噪声[1-2],该噪声具有很强的指向性,会对地面人员形成较严重的影响。在斜下降和着陆状态下,桨/涡干扰脉冲噪声占据旋翼噪声辐射的绝大部分,对军用直升机来说降低了其隐身特性,对民用直升机来说产生极大的噪声污染。因此,进行直升机旋翼降噪研究尤其是降低桨/涡干扰噪声意义重大。
众所周知,桨尖涡是直升机旋翼流场中不可忽略的流动现象,从桨尖区域逸出的强烈集中的桨尖涡不仅影响到桨叶尖部的气流流动,而且会对整个旋翼产生明显的影响,因此改变桨尖涡的空间分布就可对旋翼气动性能产生明显的影响。桨尖涡的产生与桨尖外形及其附近流动有着密不可分的关系,因而对桨尖位置进行改变可以影响桨尖涡的分布。
下反是桨叶尖部一种几何形状呈三维变化的新型桨尖形式。相对于后掠、尖削等桨尖二维平面形状,桨尖三维变化的研究开展较晚,1982年Mantay和Yeager[3]研究了矩形、后掠及尖削及后掠尖削对旋翼气动特性的影响,并首次考虑了桨尖下反对旋翼气动特性的影响,研究了矩形和下反、后掠和下反以及后掠尖削和下反桨尖组合形式的旋翼气动特性。1985年,Brocklehurst等人[4]通过风洞试验发现增加了下反的“BERP”桨尖其旋翼气特性得到了进一步改进。Muller[5-7]进一步开展了下反桨尖对旋翼悬停/前飞气动特性影响的试验,研究了下反起始位置变化给旋翼气动特性带来的影响。随着对下反桨尖三维变化的深入研究,这一技术开始逐步得到了实际应用,英国的“BERP”桨尖经过多年的发展也在最新的“BERP-IV”上采用了尖部下反设计,数值模拟表明下反设计改善了“BERP”桨尖的悬停气动性能。随着直升机旋翼气动性能的快速提升,旋翼气动噪声也成为了桨叶气动外形研究的另一个热点。Landgrebe等人[8]从降低桨尖流动速度峰值的角度设计了Ogee桨尖,取得了初步的噪声抑制效果。Tangler[9]设计了多种外形桨尖并进行了试验,他的主要思路是通过改变桨尖形状产生多个桨尖涡,以分散、减弱桨尖涡的强度,从而减弱BVI噪声。与国外相比较,国内的研究工作起步较晚,但进展迅速。例如,西北工业大学宋文萍等人[10]采用计算流体力学(Computational fluid dynamics,CFD)与计算声学相结合的Euler/Kirchhoff方法对直升机悬停状态的远场噪声进行定量计算,并研究了翼型厚度、尖削、后掠等外形变化对噪声的影响。南京航空航天大学直升机旋翼动力学国家级重点实验室提出了“CLOR”桨尖[11-12],并进行了悬停状态气动特性试验和噪声试验,取得了较好的降噪效果,但未开展具有下反桨尖形式的旋翼气动噪声特性研究。南京航空航天大学史勇杰等人[13]采用基于N-S方程/自由尾迹模型的耦合欧拉-拉格朗日数值方法计算了干扰过程中的脉冲气动载荷,初步发现采用前掠、下反桨叶的旋翼具有较好的噪声隐身特性。
相比于试验研究的高成本、长周期以及高风险,数值模拟方法具有很大的研究优势。本文采用高精度的CFD/声学类比法,通过求解Navier-Stokes方程获得旋翼噪声声源信息,将得到的声源信息传递到Farassat 1A公式中,获得旋翼的远场噪声特性。在此基础上,对不同下反桨尖的旋翼气动噪声进行了计算分析,结果表明,选择适当的下反角,可以有效地降低旋翼气动噪声,尤其是前飞斜下降状态下出现的强烈旋翼BVI噪声。
1 CFD数值模拟方法 1.1 流场求解在对噪声进行计算时,首先需要输入准确的声源信息。该声源信息由准确的CFD流场计算提供。为准确计算黏性对旋翼气动特性的影响,采用Navier-Stokes方程作为旋翼前飞流场控制方程。将坐标系定义在惯性系上,建立以绝对物理量为参数的、守恒的积分形式的N-S方程,表达式如下
| ${{\frac{d}{dt}}_{V}}QdV{{+}_{s}}F\centerdot ndS-{{F}_{v}}\centerdot ndS=0$ | (1) |
式中:
| $Q=\left[ \begin{matrix} \rho \\ \rho u \\ \rho v \\ \rho w \\ \rho E \\ \end{matrix} \right],F=\left[ \begin{matrix} \rho q \\ \rho uq+p{{i}_{x}} \\ \rho vq+p{{i}_{y}} \\ \rho wq+p{{i}_{z}} \\ \rho Hq \\ \end{matrix} \right],{{F}_{v}}=\left[ \begin{matrix} 0 \\ {{\tau }_{xx}}{{i}_{x}}+{{\tau }_{~xy}}{{i}_{y}}+{{\tau }_{xz}}{{i}_{z}} \\ {{\tau }_{yx}}{{i}_{x}}+{{\tau }_{yy}}{{i}_{y}}+{{\tau }_{yz}}{{i}_{z}} \\ {{\tau }_{zx}}{{i}_{x}}+{{\tau }_{zy}}{{i}_{y}}+\tau {{~}_{zz}}{{i}_{z}} \\ {{\varphi }_{x}}{{i}_{x}}+{{\varphi }_{y}}{{i}_{y}}+{{\varphi }_{z}}{{i}_{z}} \\ \end{matrix} \right],$ |
q=(u,v,w)T表示在直角坐标系下的速度,黏性相关项分别为τxx=2μux-(2/3)μ∇q,τxy=μ(uy+vx),φx=uτxx+vτxy+wτxz+κ∂T/∂x等;ρ表示密度;E和H分别为总能和总焓;V为控制体单元;S为单元面积;μ,κ,T分别为黏性系数、热传导系数和绝对温度。
在空间方向上采用三阶迎风单调守恒格式(MUSCL格式)与通量差分裂方法(Roe格式)相结合的方法进行离散,单调迎风差值用于确定单元面左右的状态变量
| $\begin{align} & {{U}_{R}}={{U}_{i+1}}-\frac{1}{4}\left[ \left( 1+\kappa \right){{\Delta }_{-}}+\left( 1-\kappa \right){{\Delta }_{+}} \right]{{U}_{i+1}} \\ & {{U}_{~}}L={{U}_{i}}+\frac{1}{4}\left[ \left( 1+\kappa \right){{\Delta }_{+}}+\left( 1-\kappa \right){{\Delta }_{-}} \right]{{U}_{i}} \\ \end{align}$ | (2) |
式中
| $\Delta {{~}_{+}}=\frac{{{U}_{i+1}}-{{U}_{i}}}{{{U}_{i+1}}+({{U}_{i+1}}-{{U}_{i}})/2},{{\Delta }_{-}}=\frac{{{U}_{i}}-{{U}_{i+1}}}{{{U}_{i}}-({{U}_{i}}-{{U}_{i+1}})/2}$ |
时间上采用双时间法,在伪时间方向上使用隐式LU-SGS格式进行时间推进。层流黏性系数由Sutherland定理计算得到,湍流黏性系数由Spalart-Allmaras一方程湍流模型计算。为提高流场计算效率,本文采用并行算法进行计算加速。
1.2 CFD方法算例验证为了验证本文建立的流场数值模拟方法对有升力前飞旋翼的适应性,本文采用了有风洞试验数据的AH-1G/OLS模型旋翼[14]作为计算模型。AH-1G/OLS旋翼模型有2片桨叶,桨叶平面形状为矩形,具有线性负扭转,扭转角为-10°,旋翼直径为1.916 m,弦长为0.103 9 m,展弦比为9.22。选取的计算状态对应于文献[14]的“飞行试验状态2157”,为了保持计算过程中旋翼拉力系数不变,进行了配平计算。
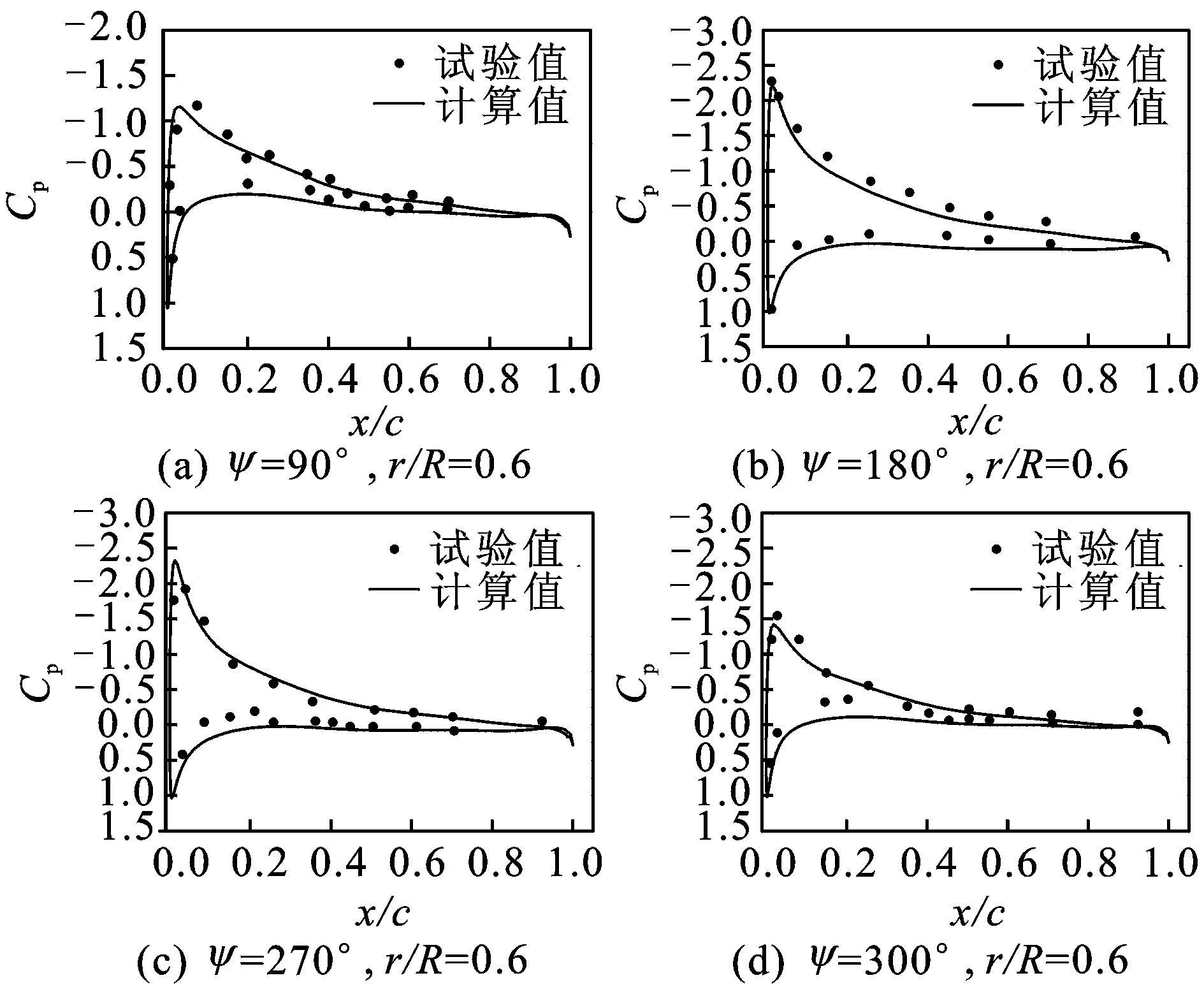
图 1给出了计算的桨叶表面压强系数分布Cp与试验值的对比结果,可以看出,对于不同方位角ψ,计算值与试验值均能很好地吻合,说明本文方法具有较高的计算精度,能适应同时带有变距和挥舞运动的有升力前飞计算,适用于出现典型BVI现象的前飞流场计算。
|
图 1 AH-1G/OLS模型旋翼前飞状态下桨叶表面压强系数分布对比 Figure 1 Comparisons of predicted and measured pressure coefficient distributions of AH-1G/OLS model rotor in forward flight |
2 气动噪声数值模拟方法 2.1 FW-H方法
本文采用基于FW-H方程声学类比法的Farassat 1A公式对旋翼的气动噪声进行数值模拟。Farassat 1A公式如下
| ${{p}^{\prime }}\left( x,t \right)={{p}^{\prime }}T\left( x,t \right)+{{p}^{\prime }}L\left( x,t \right)$ | (3) |
| $\begin{align} & 4\pi {{p}^{\prime }}_{T}\left( x,t \right)={{\int }_{f=0}}{{\left[ \frac{{{\rho }_{0}}({{{\dot{\upsilon }}}_{n}}+{{v}_{{\dot{n}}}})}{r{{\left( 1-M{{a}_{r}} \right)}^{2}}} \right]}_{ret}}dS+ \\ & {{\int }_{f=0}}\left[ \frac{{{\rho }_{0}}{{v}_{n}}(r\dot{M}{{a}_{r}}+{{c}_{0}}M{{a}_{r}}-{{c}_{0}}M{{a}^{2}})}{{{r}^{2}}{{(1-M{{a}_{r}})}^{3}}} \right]{{~}_{ret}}dS \\ & 4\pi {{p}^{\prime }}_{L}\left( x,t \right)={{\frac{1}{{{C}_{0}}}}_{f=0}}{{\left[ \frac{{{{\dot{l}}}_{r}}}{r{{\left( 1-M{{a}_{r}} \right)}^{2}}} \right]}_{ret}}dS+ \\ & _{f=0}{{\left[ \frac{{{{\dot{l}}}_{r}}-{{l}_{Ma}}}{{{r}^{2}}{{\left( 1-M{{a}_{r}} \right)}^{2}}} \right]}_{ret}}dS+ \\ \end{align}$ | (4) |
| ${{\frac{1}{{{C}_{0}}}}_{f=0}}{{\left[ \frac{{{l}_{r}}\left( rM{{{\dot{a}}}_{r}}+{{c}_{0}}M{{a}_{r}}-{{c}_{0}}M{{a}^{2}} \right)}{{{r}^{2}}{{\left( 1-M{{a}_{r}} \right)}^{3}}} \right]}_{ret}}dS$ | (5) |
式中:p′T表示厚度噪声的声压;p′L表示载荷噪声的声压;ρ0和c0分别为空气密度和音速;r为控制点到观测点的距离;Ma表示当前马赫数;Mar表示r方向马赫数;Lr表示桨叶表面沿传播方向的载荷分量;(·)代表对时间的导数;下标ret代表延迟时间。
本文采用旋转积分面方法,选取桨叶表面为旋转积分面,从桨叶表面的贴体网格上提取声源信息。
2.2 FW-H方法算例验证为了验证本文建立的噪声数值模拟方法对有升力前飞旋翼噪声计算的有效性,选择出现BVI现象的AH-1G/OLS模型旋翼典型试验状态10 014,该计算状态参数[15]为:Matip=0.644,μ=0.164,αTPP=1°,CT=0.005 4,Re=1.6×106。该试验状态中旋翼不仅有周期性的变距运动,而且有周期性的挥舞运动。旋翼桨叶的变距和挥舞的规律如下:θ(t)=6.14°+0.9cosψ(t)-1.39sinψ(t),β(t)=0.5°-1.0cosψ(t)。观察点坐标分别为MIC3(0,27.467c,-15.858c)和MIC7(13.733c,23.787 c,-15.858
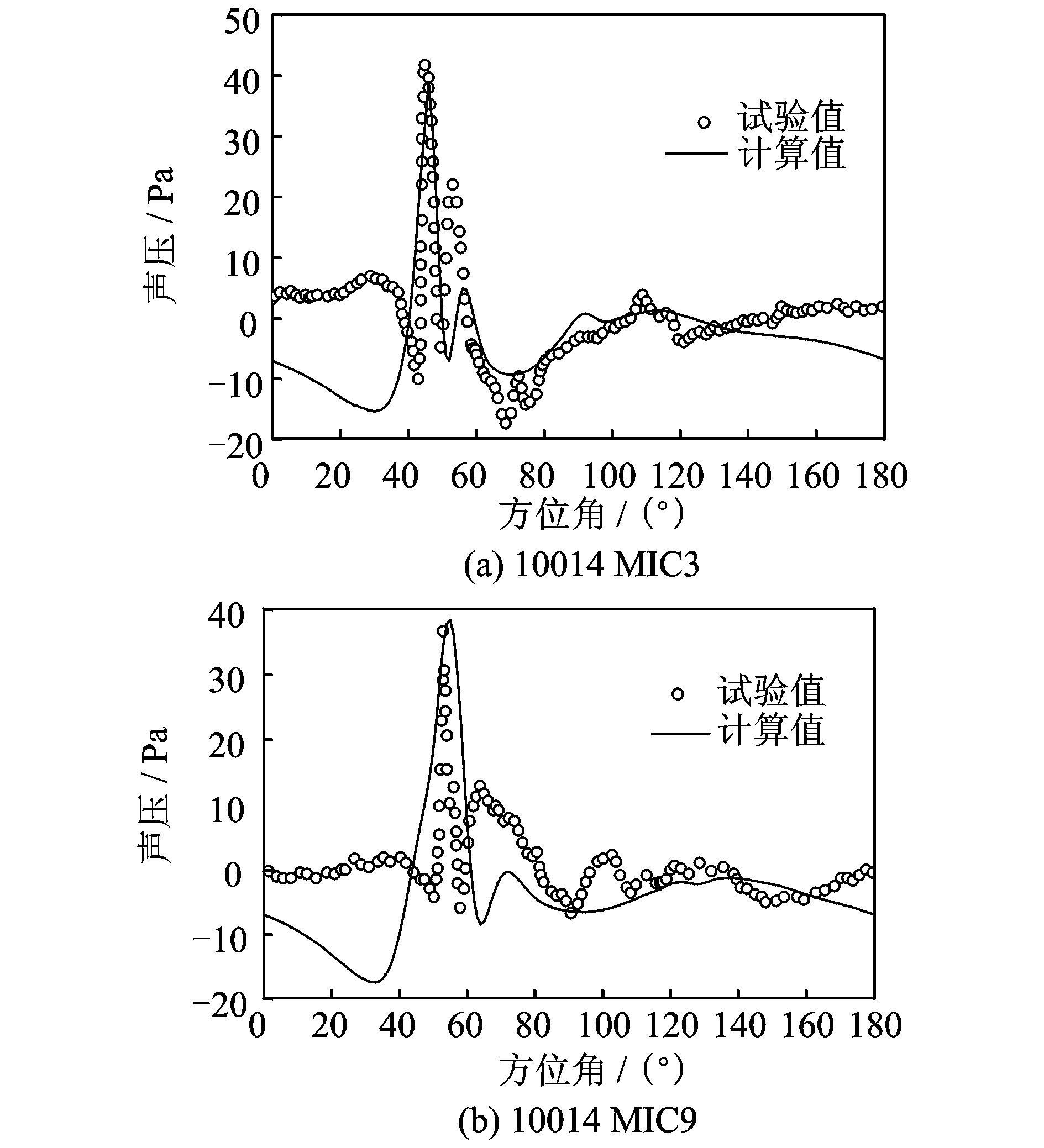
图 2给出了旋翼噪声在不同观测位置的声压变化历程的计算值与试验值的对比结果。通过对比可以看出,本文采用Farassat 1A公式计算的旋翼BVI噪声声压幅值和试验结果基本吻合。在相位和幅值上均能较为准确地计算出AH-1/OLS在该状态下45°方位角左右处的声压正峰值,这也是桨/涡干扰状态的典型特征,这表明该计算方法可以较好地体现BVI噪声的主要特性,只是在复杂的BVI局部细节变化之处有所差别。
|
图 2 出现BVI现象的AH-1G/OLS旋翼前飞声压时间历程对比 Figure 2 Comparisons of predicted and measured time histories of sound pressure of AH-1G/OLS model rotor in forward flight |
3 下反桨尖对旋翼BVI噪声的影响
本文计算对比了在前飞状态,尤其是在针对发生强BVI的斜下降飞行状态下,不同的桨尖下反参数对旋翼噪声尤其是BVI噪声的影响。本文首先给出无下反情况下常规矩形桨叶和抛物后掠尖削桨叶的对比,然后计算对比了不同下反角情况下抛物后掠尖削桨叶对BVI噪声的影响规律,桨叶外形如图 3所示。

|
图 3 常规矩形桨叶和抛物后掠尖削桨叶外形的对比 Figure 3 Shape comparison of conventional rectangular blade and parabolic taper-swept blade |
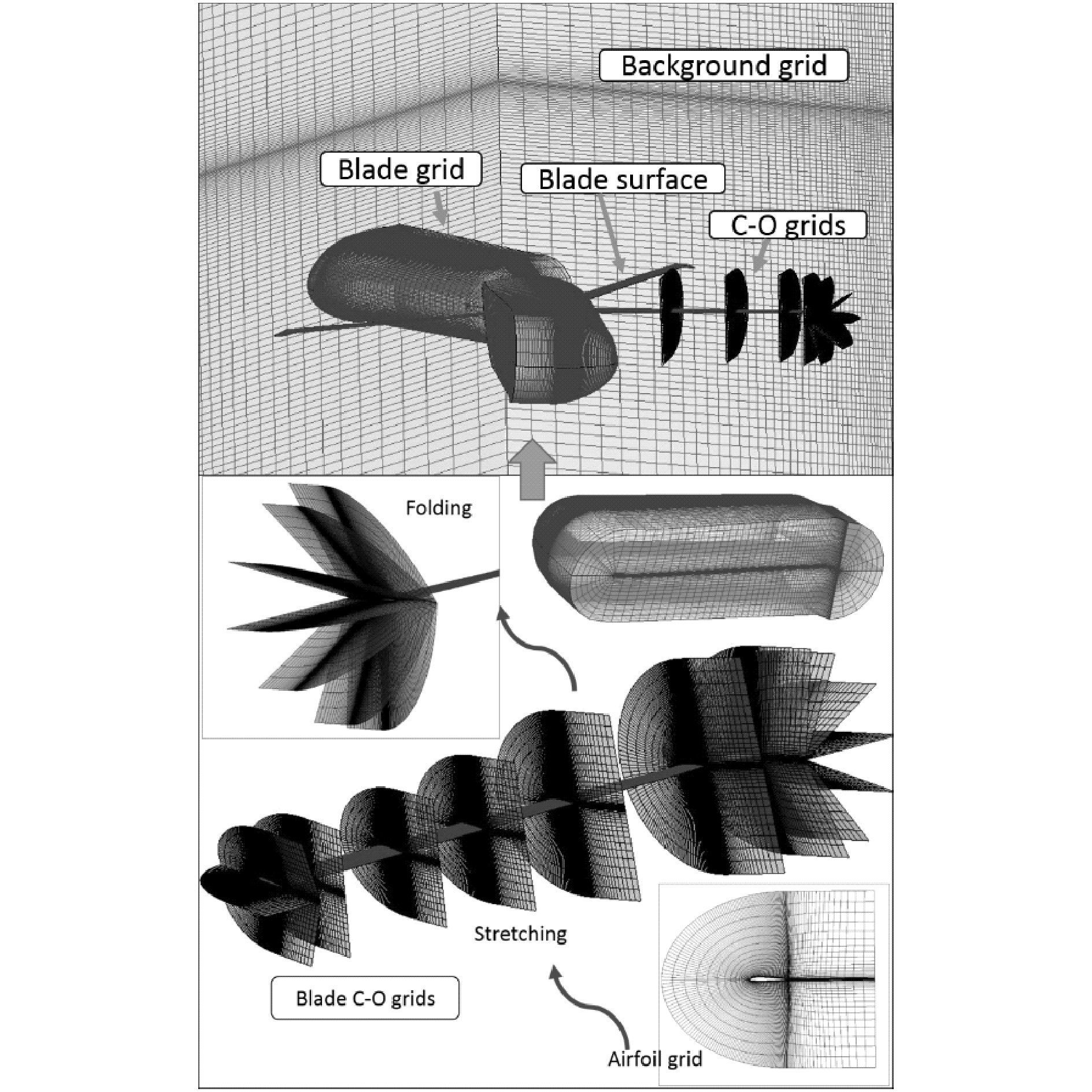
计算参数如下:旋翼为5片桨叶,桨尖马赫数为0.636。旋翼半径不变,下反位置在0.95R 处。对前飞斜下降进场状态进行计算分析和比较,总距为11°,轨迹角为6°,前进比为0.102 1。本文分别给出了常规矩形桨尖无下反和抛物后掠无下反、下反角20°,30°等不同桨叶参数情况下的旋翼噪声。观测点位置为距旋翼桨毂3.09R距离的半圆,从桨盘平面到桨盘正下方(Y轴方向为前飞方向)。CFD计算所用运动嵌套网格如图 4所示。
|
图 4 整体运动嵌套网格示意图 Figure 4 Overall schematic of moving-embedded grid system |
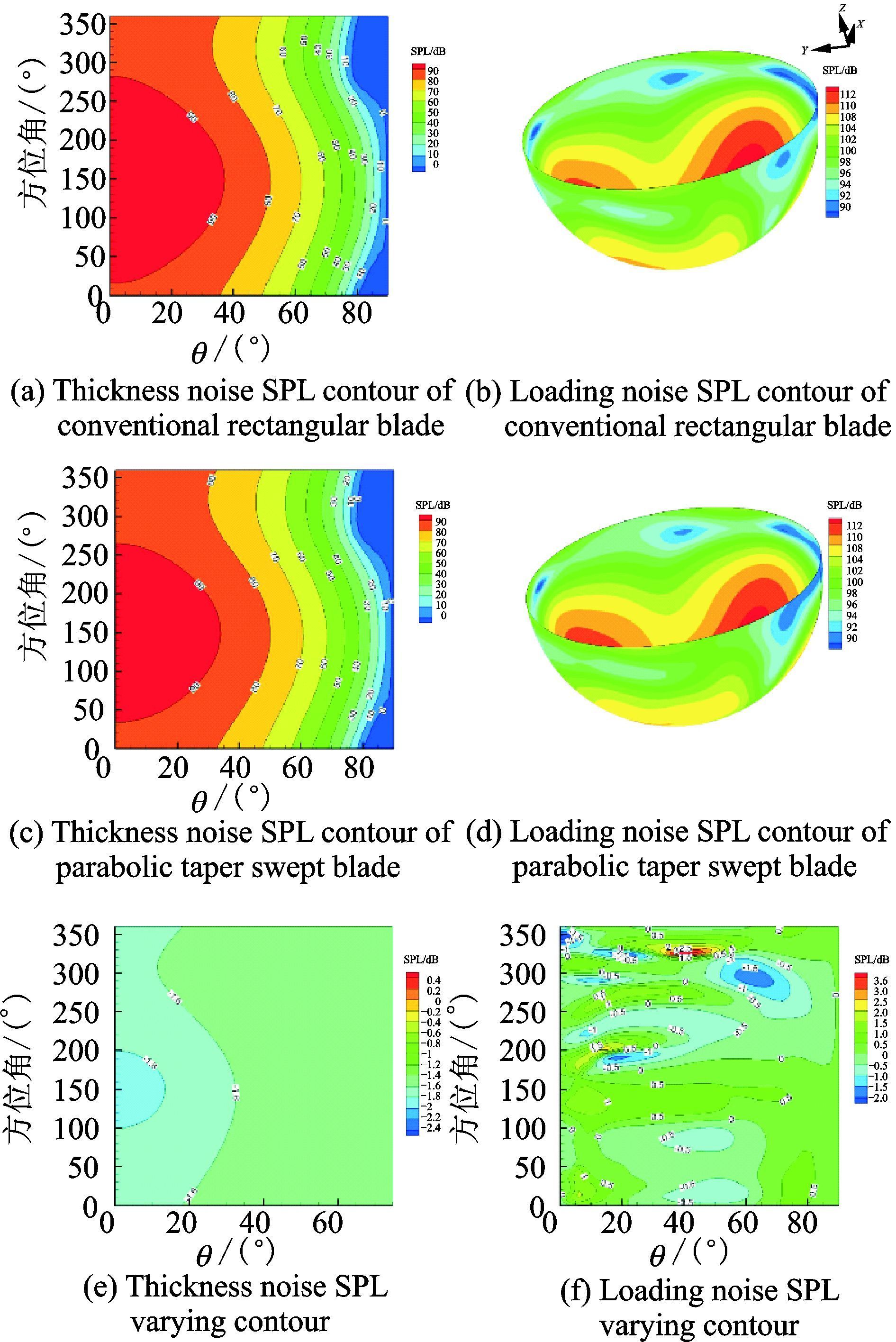
图 5给出了无下反情况下常规矩形桨叶和抛物后掠尖削桨叶的旋翼气动噪声声压级(Sound pressure level,SPL)对比结果。图中横坐标为桨盘平面至桨盘正下方的角度,纵坐标为噪声观察位置相对于桨叶初始位置的方位角,与桨叶的方位角一致。从旋翼厚度噪声投影到平面上的声压级云图可以看出:厚度噪声主要分布在桨盘平面内,离桨盘平面越远,厚度噪声越小;在相同飞行条件下,抛物后掠尖削桨尖旋翼较矩形常规旋翼桨尖旋翼相比,厚度噪声在桨盘平面内减小了近2 dB,这说明抛物后掠尖削桨尖可以有效地降低旋翼的厚度噪声。从载荷噪声的声压级分布云图可以发现:在上述计算条件下,旋翼的前下方尤其是前行侧的前下方载荷噪声比较大,大的载荷噪声主要分布在旋翼前行侧(20°~180°方位角),这与BVI噪声的发生位置和传播方向一致;而与常规矩形桨叶相比,抛物后掠尖削桨叶降低载荷噪声从而降低BVI噪声的效果很小。基于此,对抛物后掠尖削桨尖进行不同下反设计,以期得到有效的可降低BVI噪声的桨尖设计方案。
|
图 5 无下反情况下常规矩形桨叶和抛物后掠尖削桨叶的噪声SPL云图对比 Figure 5 SPL contour comparison between conventional rectangular and parabolic taper swept blades without anhedral angle |
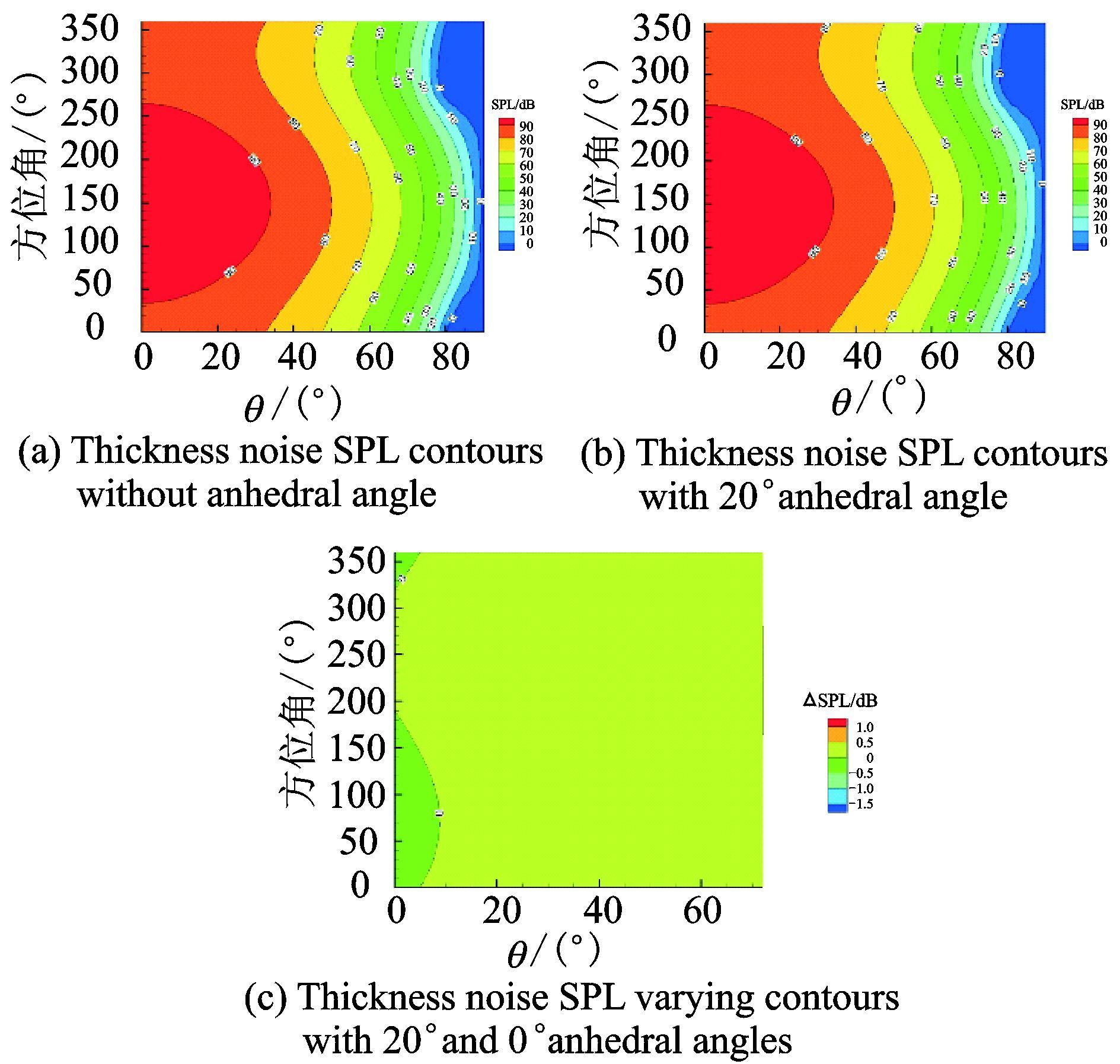
图 6给出了抛物后掠尖削桨叶在无下反角与20°下反角时旋翼厚度噪声投影到平面上的声压级云图对比结果。如图 6(c)所示,两种情况下旋翼的厚度噪声分布没有明显变化,说明下反形式对旋翼的厚度噪声几乎没有影响。
|
图 6 旋翼厚度噪声云图对比 Figure 6 Comparison of rotor thickness noise contours |
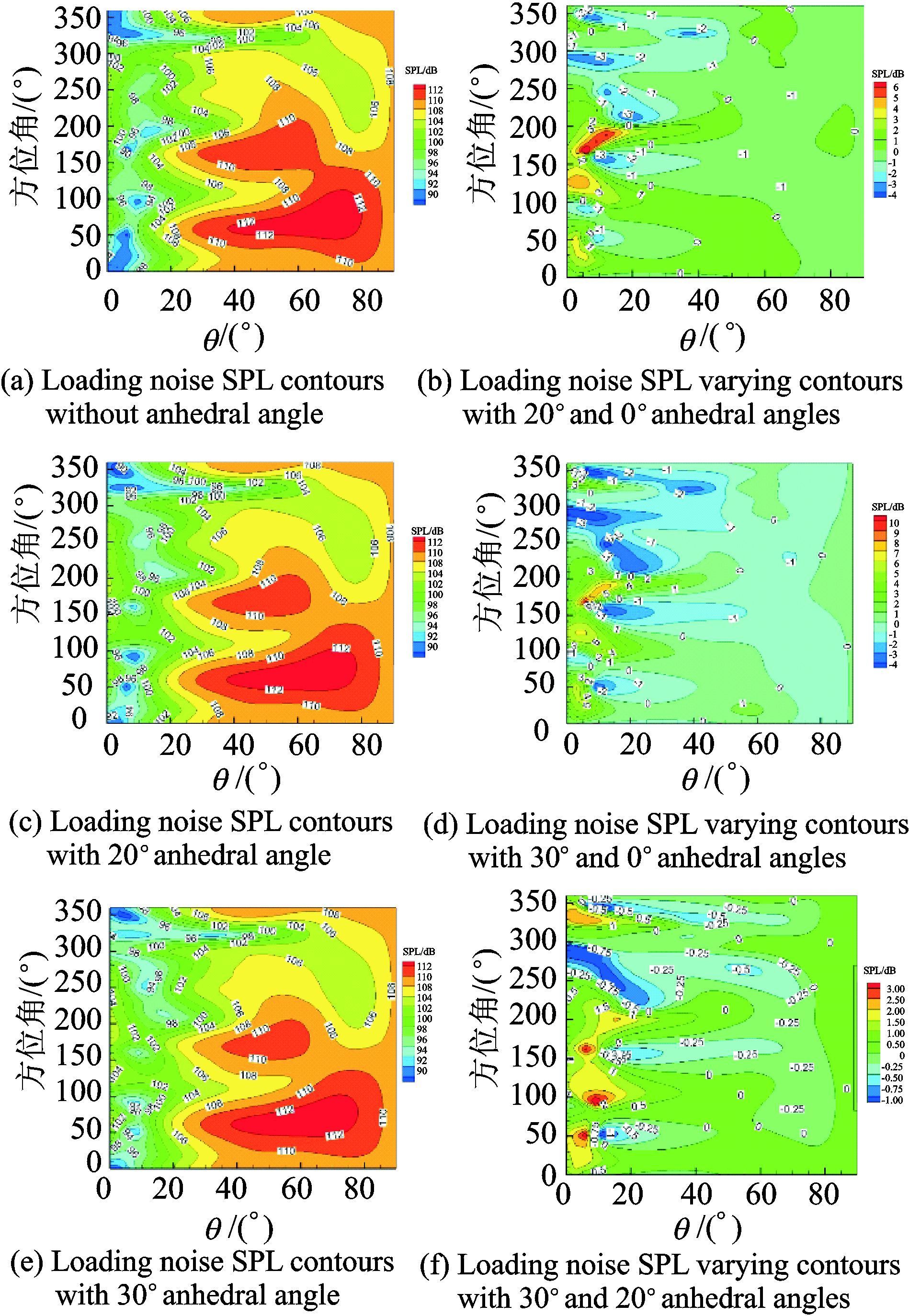
图 7给出了不同下反角度的旋翼载荷噪声投影到平面上的声压级云图对比结果。可以看出,相比于无下反角的桨叶,有下反角的桨叶绝大部分地方噪声得到有效降低,尤其是图 7(a,c,e)中的红色区域,而该处正好是噪声最大的地方,噪声可降低1~2 dB。当然,少部分区域的噪声增大,但这几个小区域其原本的噪声值与最大噪声辐射点(110 dB左右)相比小很多,因而即使增大了噪声,但是与噪声最大值相比仍较小。例如在方位角170°、桨叶下方6°左右的位置,20°下反的旋翼噪声增加最大,达到6 dB左右,但是该处原来的噪声只有90 dB,所以最后的总噪声96 dB相对其他位置的噪声来说并不大,而其余大部分位置的噪声都有所降低,有些地方可以降低3 dB左右。
|
图 7 不同下反角桨叶载荷噪声降低的声压级云图对比 Figure 7 Comparison of loading noise contours with different anhedral angles |
从图 7中30°和20°不同下反角度噪声差值投影到平面上的声压级对比可以看出:下反角度越大,在绝大部分区域降噪效果越明显;只是在原先噪声比较小的位置,噪声声压级有所增加。综上,下反角度越大,对前飞状态的旋翼噪声降低越明显。
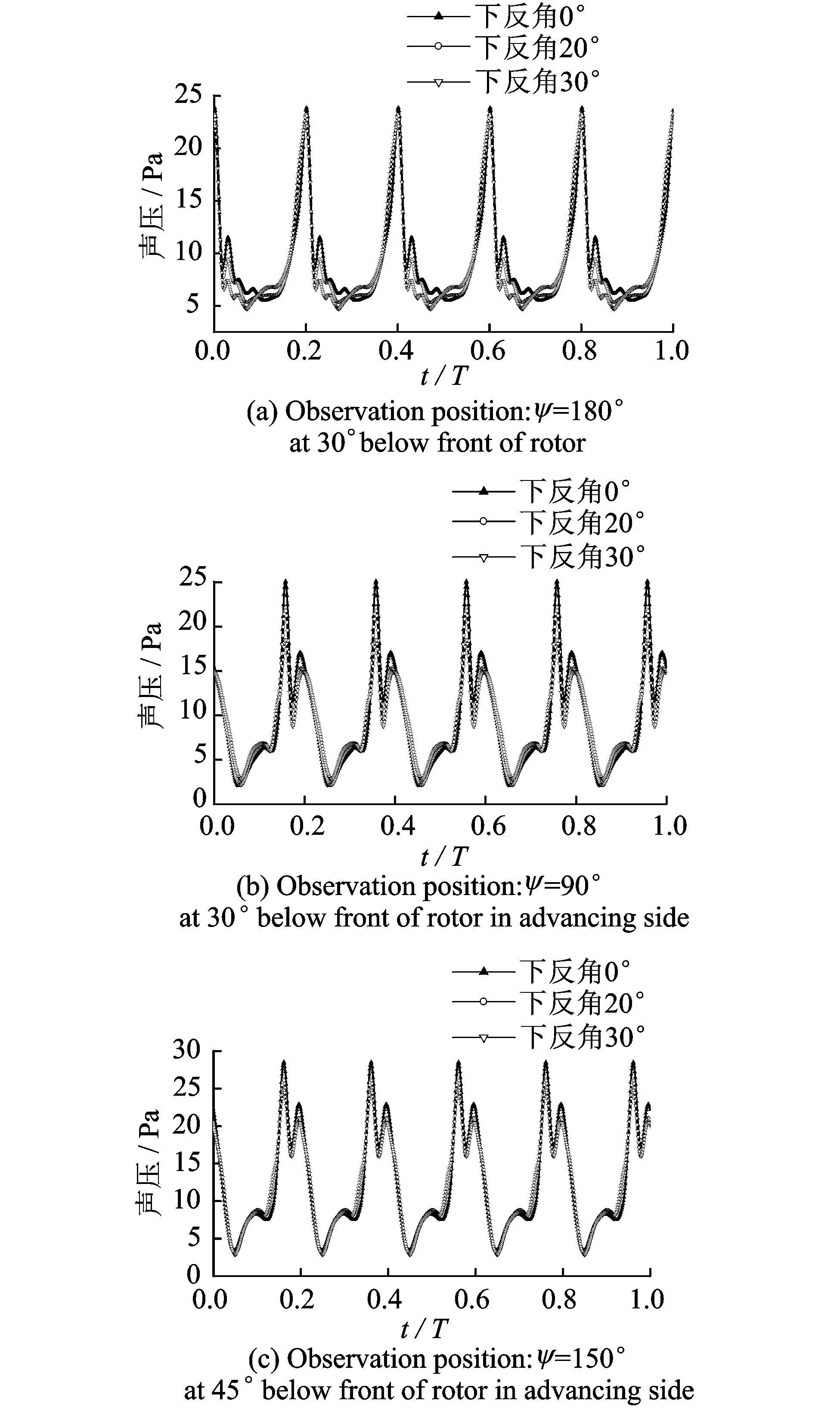
为了研究下反桨尖降低BVI噪声的降噪机理,本文分析对比了旋翼正前下方、前行侧下方等3个不同观察点位置的声压时间历程,如图 8所示,图中给出的观察点均为桨/涡干扰噪声的噪声热点,观察点距离桨毂中心3.09R。从图 8可以看出,在这些发生强BVI噪声的区域,具有下反桨尖的旋翼,其噪声声压峰值明显变小,并且下反角度越大,噪声声压峰值越小。结果表明下反角可以有效地降低旋翼气动噪声,尤其是噪声比较明显的前飞斜下降状态下的旋翼BVI噪声。
|
图 8 桨-涡干扰噪声热点位置声压时间历程对比 Figure 8 Comparison of sound pressure time history on BVI noise hotspot |
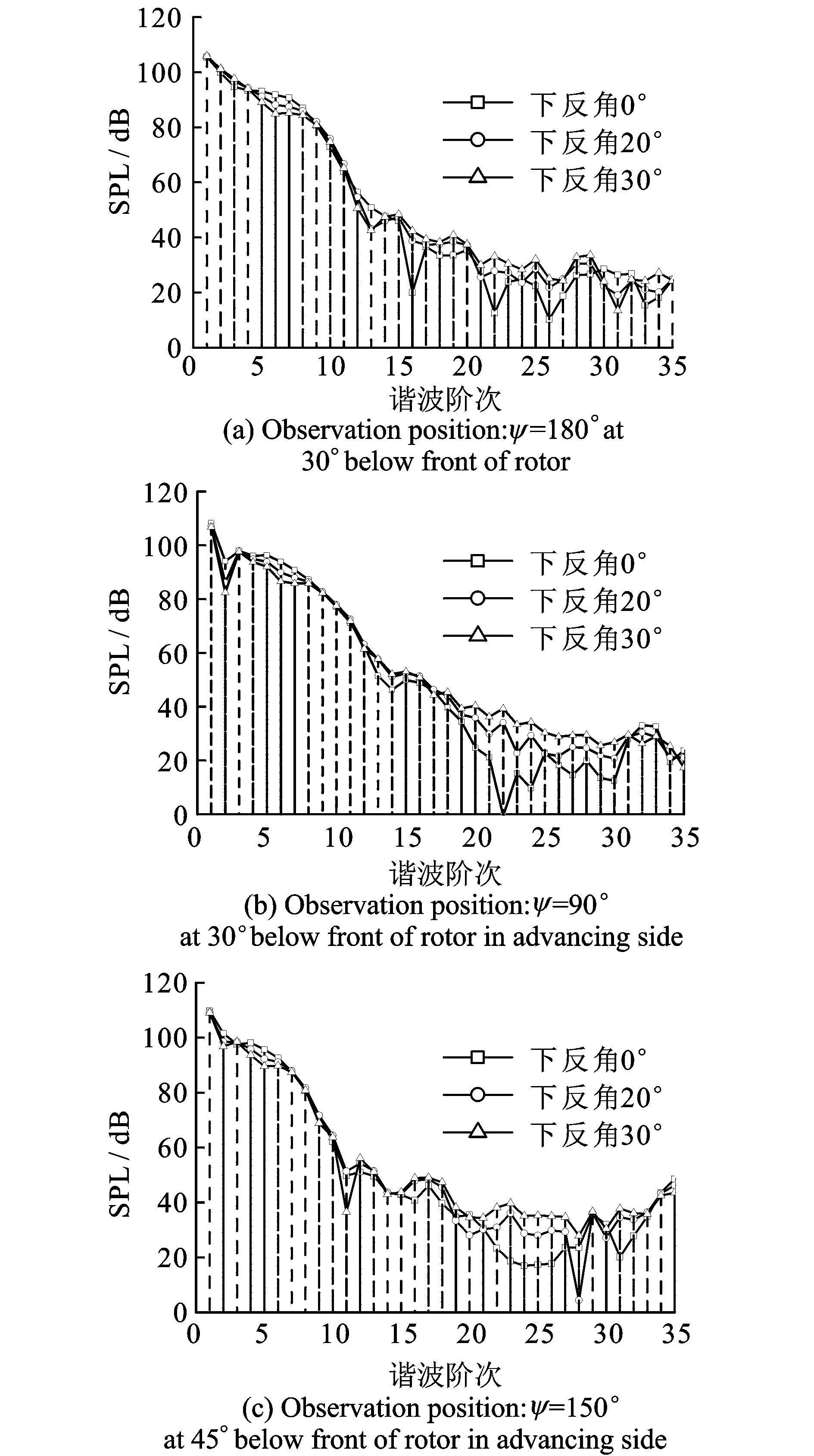
图 9给出了不同观察位置上不同下反角情况下的频谱分析对比图。从图 9中可以看出,在低、中频区域,下反角越大,声压级幅值越小;而在高频区域,下反角越大,声压级幅值越大。高频声压可以很快耗散掉,且高频区的声压级相对较小,所以低、中频声压起主导作用。由于低、中频声压级随下反角增大而减小,所以总声压级降低。
|
图 9 BVI噪声频谱对比 Figure 9 Comparison of BVI noise frequency spectrum |
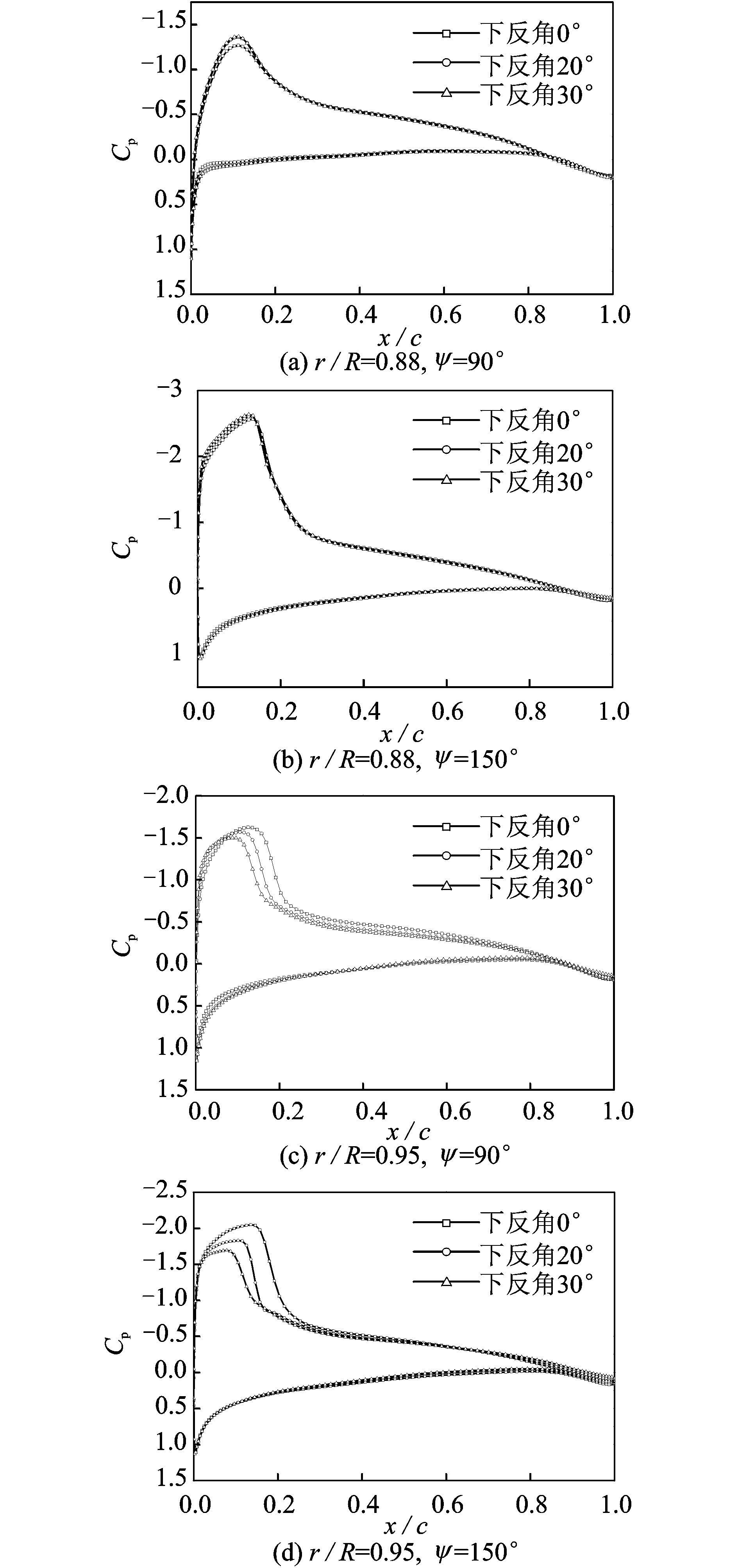
图 10给出了不同下反角度的桨叶在不同方位角和不同径向位置处桨叶剖面的压强分布。所取径向位置分别为r/R=0.88和r/R=0.95。从图 10(a,b)中可以看出,下反位置(0.95R处)内侧的表面负压增强,这有利于升力的增加;从图 10(c,d)中可以看出,下反位置的桨叶表面负压减弱,这有利于减小桨叶尖端的载荷。
|
图 10 不同位置处桨叶剖面压强系数的对比 Figure 10 Comparisons of pressure coefficient distributions at different blade section positions |
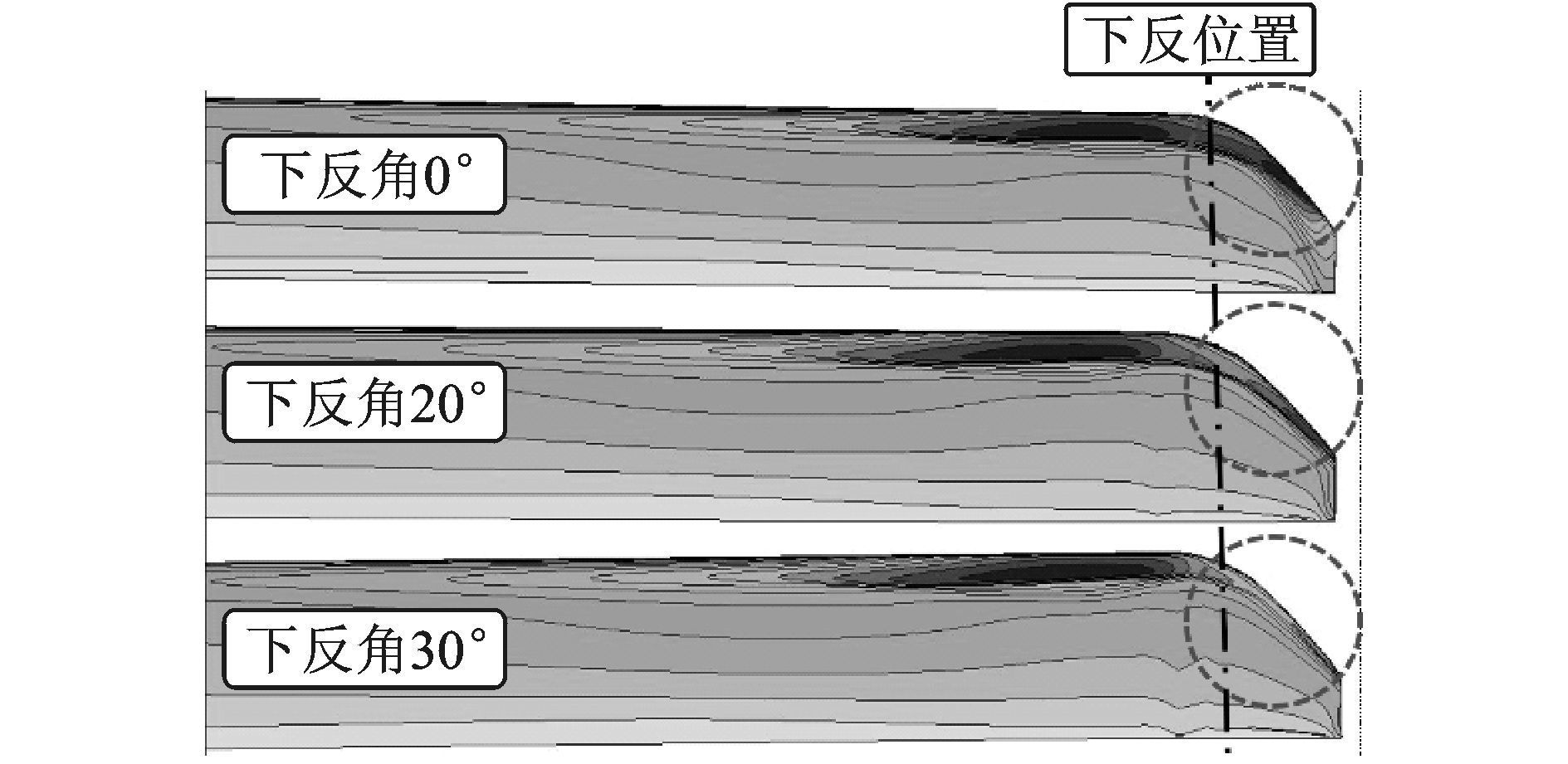
图 11给出了90°方位角处不同下反角的桨叶上表面的压强等值线分布图。从图中可以看出,下反对内侧的低压区域起到负压增强的效果;随着下反角度的增加,对桨叶尖部压强分布的改善效果越明显。
|
图 11 90°方位角处不同下反角对应的桨叶上表面压强分布 Figure 11 Pressure distributions on surface of blade with different anhedral angles under azimuth angle of 90° |
图 12显示了不同下反角桨叶与桨尖涡的位置关系。虚线长框处表示该时刻桨叶所在的位置(方位角72°),虚线圈表示前面的桨叶脱出的涡此刻相对于桨叶的位置。可以发现,下反桨尖的桨尖涡产生位置低于旋翼桨盘,这增加了桨尖涡到桨盘的距离,因此可以减弱桨尖涡对旋翼桨叶的干扰作用。且随着下反角的增大,桨尖涡到桨盘的垂直距离增大,从而减小了BVI 噪声。

|
图 12 桨叶与桨尖涡位置关系图 Figure 12 Position between blade and blade-tip vortex |
4 结论
(1) 通过对旋翼流场及噪声的数值模拟方法进行计算验证,表明本文建立的数值模拟方法可有效地用于BVI状态下的旋翼流场及噪声特性计算。
(2) 在桨盘前行侧的前下方,下反桨尖旋翼气动噪声降低明显,而此处正好是BVI噪声的辐射区,这说明下反桨尖旋翼可以有效地减小旋翼前飞状态下的BVI噪声。
(3) 在低、中频区域,下反角越大,声压级幅值越小;而在高频区域,下反角越大,声压级幅值越大;低、中频声压起主导作用。由于低、中频声压级随下反角增大而减小,所以总声压级降低。
(4) 下反桨尖的桨尖涡产生位置低于旋翼桨盘,这增加了桨尖涡到桨盘的距离,因此可以减弱桨尖涡对旋翼桨叶的干扰作用。
| [1] | Megan S M. Helicopter blade-vortex inter action noise with comparisons to CFD calculations [R]. NASA-TM-110423, 1996. |
| [2] | Yung H Y. rotor blade-vortex interaction noise[J]. Progress in Aerospace Science , 2000, 36 : 97–115. DOI:10.1016/S0376-0421(99)00012-3 |
| [3] | Mantay W R, Yeager J W T. Parametric tip effects for conformable rotor applications [R]. N ASA-TM-85682, 1983. |
| [4] | Brocklehurst A, Barakos G N. A review of helicopter r otor blade tip shapes[J]. Progress in Aerospace Sciences , 2013, 56 (1) : 37–74. |
| [5] | Muller R H G, Staufenbiel R. The influence of winglets on rotor Aerodynamics[J]. Ve rtica , 1987, 11 (4) : 601–618. |
| [6] | Mueller R H G. Winglets on rotor blades in forwar d flight—A theoretical and experimental investigation[J]. Vertica , 1990, 14 (1) : 31–46. |
| [7] | Muller R H G. Special vortices at a helicopter rotor blade[J]. Journal of the American Helicopter Society , 1990, 35 (4) : 16–22. DOI:10.4050/JAHS.35.16 |
| [8] | Landg rebe A J, Bellinger E D. Experimental investigation of model variable-geometry a nd ogee tip Rotors [R]. NASA-CR-2275 74N18645,1974. |
| [9] | Tangler J L, Woblfeld R M, Miley S J. An experimental investigation of vortex stability, tip shapes, compressibility and noise for hovering model rotors [R]. NASA-CR-2305 73N29996, 1973. |
| [10] |
宋文萍, 韩忠华, 王立群, 等.
旋翼桨尖几何形状对旋翼气动噪声影响的定量计算分析[J]. 计算物理 , 2001, 18 (6) : 569–572.
Song Wenping, Han Zhonghua, Wang Liqun, et al. The effect of blade -tip shape on rotor aeroacoustic noise by Euler/Kirchhoff method[J]. Chinese Journal of Computational Physics , 2001, 18 (6) : 569–572. |
| [11] |
招启军, 徐国华.
新型桨尖旋翼悬停气动性能试验及数值研究[J]. 航空学报 , 2009, 30 (3) : 422–429.
Zhao Qijun, Xu Guohua. Aerodynamic performance of rotor with new type b lade-tip in hover based upon test and numerical investigations[J]. Acta Aeron autica et Astronautica Sinica , 2009, 30 (3) : 422–429. |
| [12] |
招启军, 徐国华.
具有特型桨尖旋翼悬停状态气动噪声的初步试验研究[J]. 空气动力学学报 , 2009, 27 (3) : 320–324.
Zhao Qijun, Xu Guohua. The primary experiments on aeroacoustic of rotor with unconventional blade-tip in hover[J]. Acta Aerodynamica Sinica , 2009, 27 (3) : 320–324. |
| [13] |
史勇杰, 苏大成, 徐国华.
桨叶气动外形对直升 机桨-涡干扰噪声影响研究[J]. 南京航空航天大学学报 , 2015, 47 (2) : 235–242.
Shi Yongjie, Su Da cheng, Xu Guohua. Research on influence of shape parameters on blade-vortex inte raction noise of helicopter rotor[J]. Journal of Nanjing University of Aerona utics & Astronautics , 2015, 47 (2) : 235–242. |
| [14] | Yeo H, Romander E A, Norman T R. Investigation of rotor performance and loads of a UH-60A individual blade control system[J]. Journal of the American Helicopter Society , 2011, 56 (4) : 1–18. |
| [15] | Yu Y H, Tung C, Gallman J, et al. Aerodynamics and acousti cs of rotor blade-vortex interactions[J]. Journal of Aircraft , 1995, 32 (5) : 970–977. DOI:10.2514/3.46825 |
 2016, Vol. 48
2016, Vol. 48


