普通铰接式或弹性轴承旋翼直升机,其机体侧向二阶模态频率较高,相应地与摆振后退型模态频率重合点(共振)转速也较高,要完全消除该耦合动不稳定区,就需要提供很大桨叶摆振和机体阻尼,难以实现。一般的处理方法是尽量提高机体侧向二阶模态频率,把相应的不稳定区全部“赶出”最大转速以外,并具有足够的转速裕度,同时在最大工作转速以内系统具有足够的阻尼裕度,保证了直升机在整个使用范围内不发生地面共振[1-3]。
直升机重量大或发动机功率不足以使直升机垂直起飞时,往往采用滑跑起飞。直升机滑跑不仅会影响其横向平衡[4],更为严重的是会影响到直升机地面共振稳定性[5]。根据前轮摆振动力学理论[6],直升机滑跑时,起落架机轮侧向刚度会随着速度的提高而降低,因而会降低机体侧向模态的频率。机体侧向二阶模态频率降低会降低共振转速,使原来高于工作转速的不稳定边界有可能进入到工作转速以内而发生地面共振。大载重时往往是需要采取滑跑起飞方式,而大重量时侧向二阶固有频率低,因而是最不利的情况[7]。因此,为避免直升机发生滑跑地面共振,就需要研究滑跑速度对机体侧向模态频率以及地面共振的影响,以便确定滑跑的限制速度。
本文根据机体质量特性参数、起落架缓冲支柱和机轮刚度和阻尼的试验数据,采用等效方法分析直升机地面滑跑情况下机体侧向二阶模态频率。
1 地面滑跑平衡分析为了使直升机以不同的速度V实现定常滑跑,旋翼须具有一定拉力,并使拉力向前倾斜一定的角度。拉力的前向分量与直升机气动阻力及地面摩擦力相平衡时,直升机就以稳定的速度滑跑。通过旋翼总距及周期变距的操纵,可使旋翼产生一定的拉力及拉力倾斜,但不同操纵、不同的滑跑速度以及尾桨拉力会改变直升机的平衡状态,影响到前起落架和主起落架的载荷大小,进而改变起落架缓冲支柱和轮胎的刚度和阻尼特性。
一般情况下,直升机滑跑时的旋翼拉力应控制在直升机重量的20%~30%以下。根据文献[7]的计算结果发现,在停机情况下,拉力重量比低于20%时,机体侧向二阶固有频率变化很小。另外,根据文献[7]关于舰面状态直升机机体模态频率的分析结果发现,在一定范围内,仅因横航向平衡引起的起落架载荷的变化,不会降低机体侧向二阶模态频率,并且增加的量值很小。因此,简化分析时只考虑旋翼拉力及拉力方向对起落架载荷的影响,暂不考虑直升机横航向平衡引起的起落架载荷变化。因低速滑跑时作用在直升机上的空气阻力远小于地面摩擦力,可忽略空气阻力的影响。
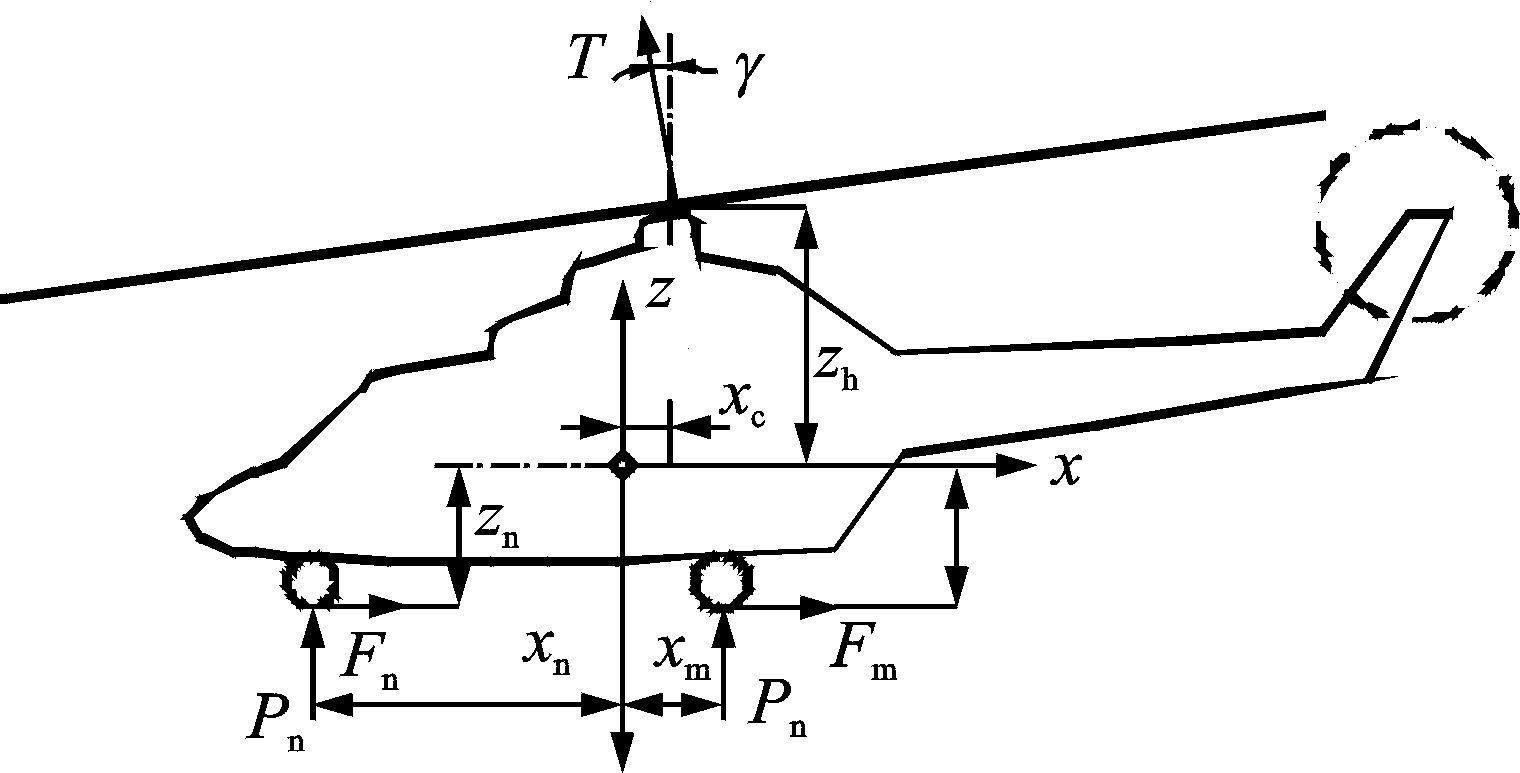
直升机以不同速度V滑跑时,轮胎与地面的摩擦因数不同,因而摩擦力也不同。旋翼拉力大小和方向的不同组合,可克服轮胎摩擦力而保持定常滑跑。由于旋翼轴存在前倾角γ,在不改变旋翼拉力方向的情况下,仅需改变旋翼拉力的大小就可与地面摩擦力保持平衡。即最简单的操纵方式是,仅由总距操纵就能实现定常或加速滑跑。根据以上的分析,直升机滑跑时可进行简化处理,忽略其横侧向及航向平衡带来的左、右起落架载荷的差异,同时不考虑机身的气动阻力,得到直升机纵向力和力矩的平衡如图 1所示。图中:T表示旋翼拉力;γ表示旋翼轴前倾角;G表示直升机重力;Pn、Pm分别表示前、主起落架垂向载荷;Fn、Fm表示前、主轮与地面的摩擦力。
|
图 1 直升机定常滑跑时的平衡状态 Figure 1 Helicopter longitudinal balance during steady running |
设前、主轮完全相同,则机轮与地面的摩擦因数均为f,考虑到各起落架有两个完全相同的机轮,则前、主轮与地面之间的摩擦力分别为:Fn=fPn及Fm=fPm。可以方便地建立纵平面内的力和力矩平衡方程组为
| $\left\{ \begin{align} & Tsin\gamma -{{F}_{n}}-2{{F}_{m}}=0 \\ & Tcos\gamma +{{P}_{n}}+2{{P}_{m}}-G=0 \\ & T({{x}_{m}}-{{x}_{c}})cos\gamma -T({{z}_{h}}+{{z}_{m}})sin\gamma + \\ & {{P}_{n}}({{x}_{n}}+{{x}_{m}})-G{{x}_{m}}=0 \\ \end{align} \right.$ | (1) |
给出轮胎与地面的摩擦因数与滑跑速度的关系后,结合起落架缓冲支柱及轮胎的静压缩实验曲线,可以采用式(1)计算给定速度下的旋翼拉力、起落架载荷、缓冲支柱和轮胎的压缩量等参数。
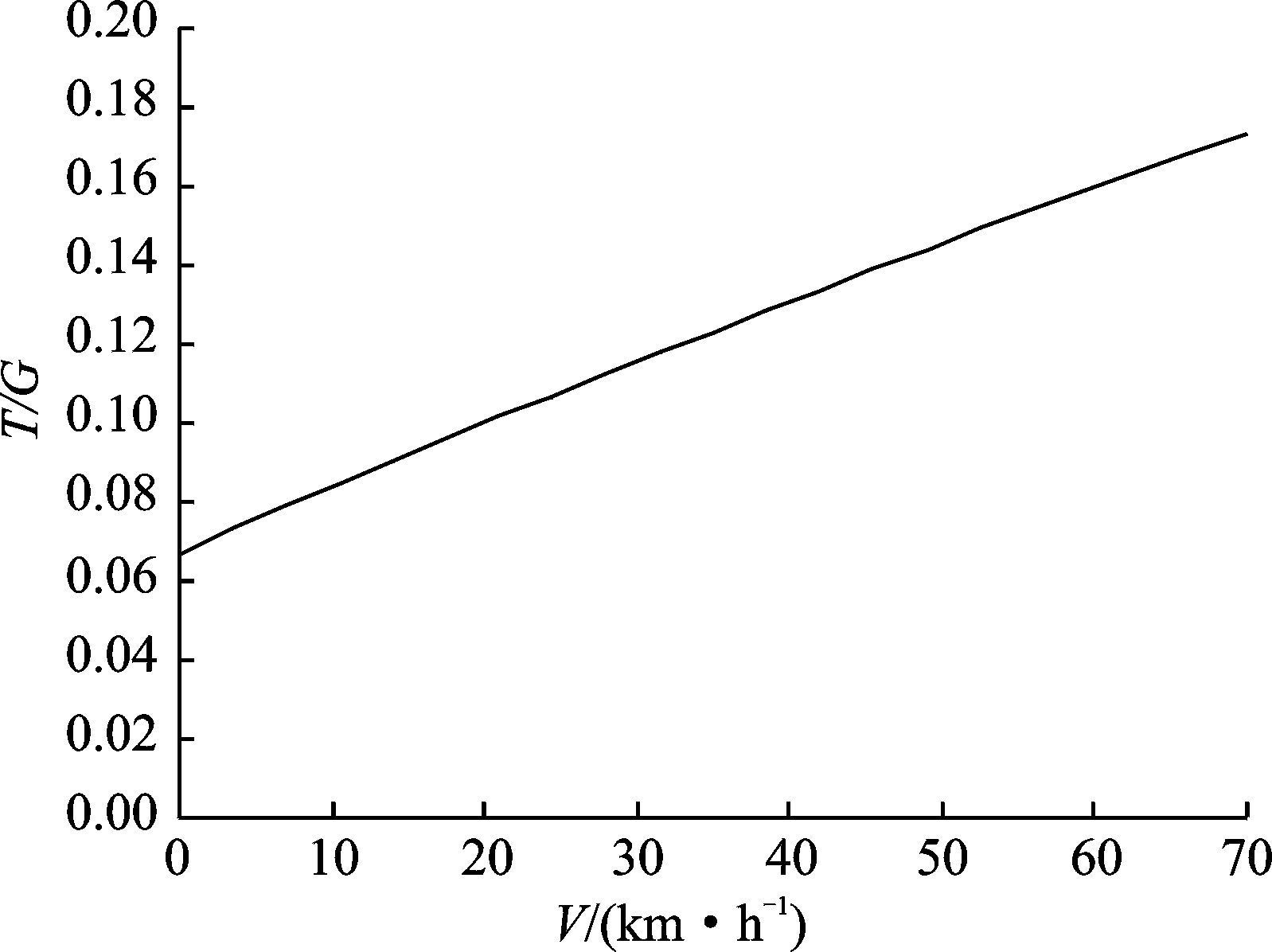
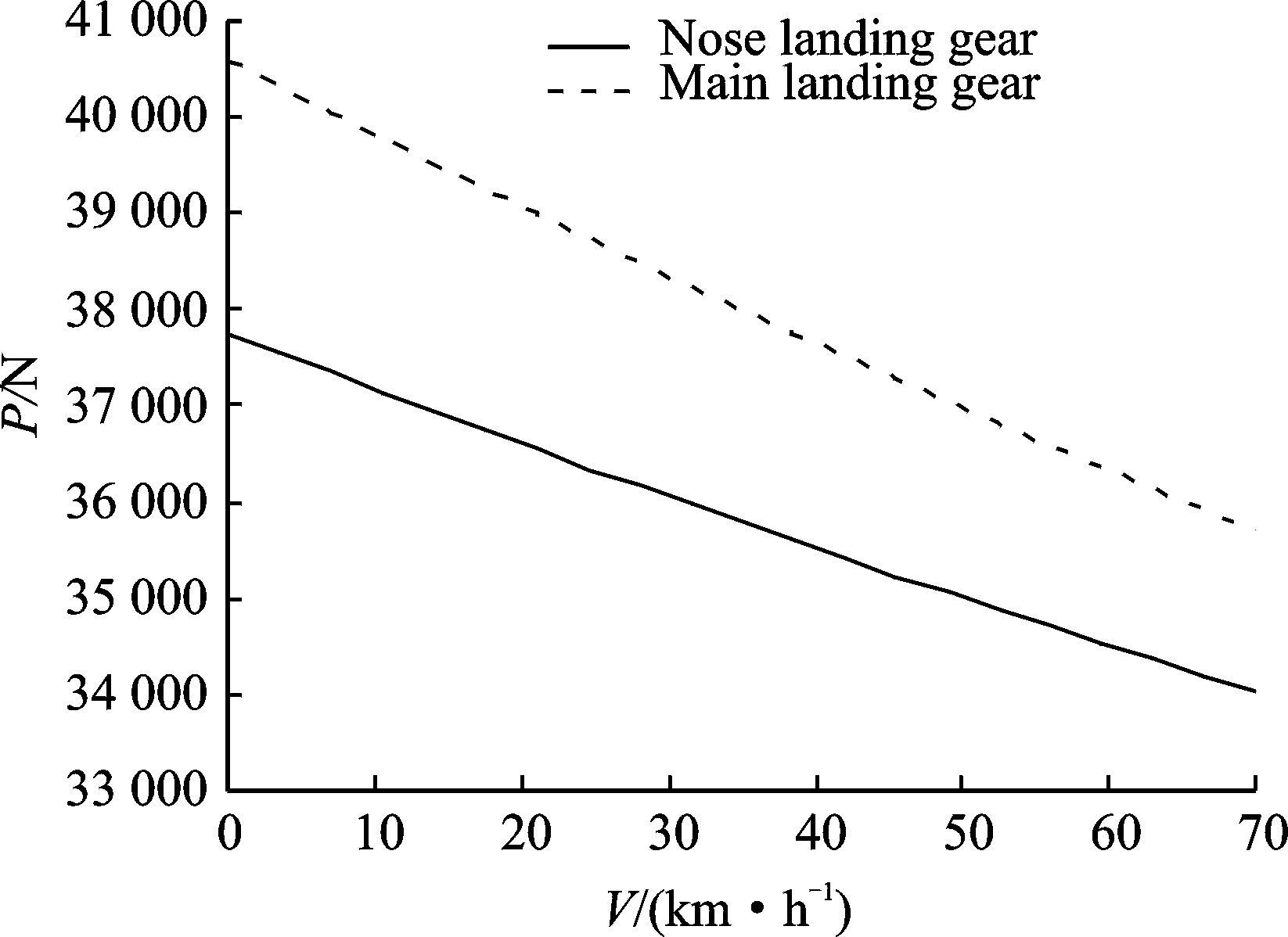
假定滑跑时轮胎处于纯滚动状态,轮胎滚动阻力系数取决于跑道的表面和轮胎的型式。在标准跑道上,滚动阻力系数在0.008~0.020之间,滚动阻力系数随滑跑速度的增加而增加[8]。图 2,3分别表示旋翼拉重比(T/G)及前、主起落架载荷P随滑跑速度的变化。
|
图 2 T/G随滑跑速度的变化 Figure 2 Change of T/G with velocity |
|
图 3 起落架载荷随滑跑速度的变化 Figure 3 Chang of vertical load on landing gear with velocity |
从图 2发现,随着滑跑速度的增加,旋翼拉力增加。由于轮胎滚动阻力系数随滑跑速度的增加而提高,假定旋翼拉力的前倾角始终与旋翼轴前倾角相同,故旋翼拉力也相应地随滑跑速度的提高而增加。另外还发现,仅有总距操纵、不用周期变距操纵,就能使直升机实现稳定滑跑。而且一直到速度为70 km/h时,拉力重量比T/G都不超过20%。
从图 3看到,前、主起落架载荷随滑跑速度的增加而下降。一方面,速度提高时需增加旋翼拉力,相应地会降低起落架的地面支反力;另一方面增加旋翼拉力会提高直升机的低头力矩,该低头力矩会使主起落架载荷有些降低,而使前起落架载荷产生不大的附加增量。从载荷曲线上看到,随速度的提高,主起落架载荷比前起落架载荷下降更快,曲线斜率更大。
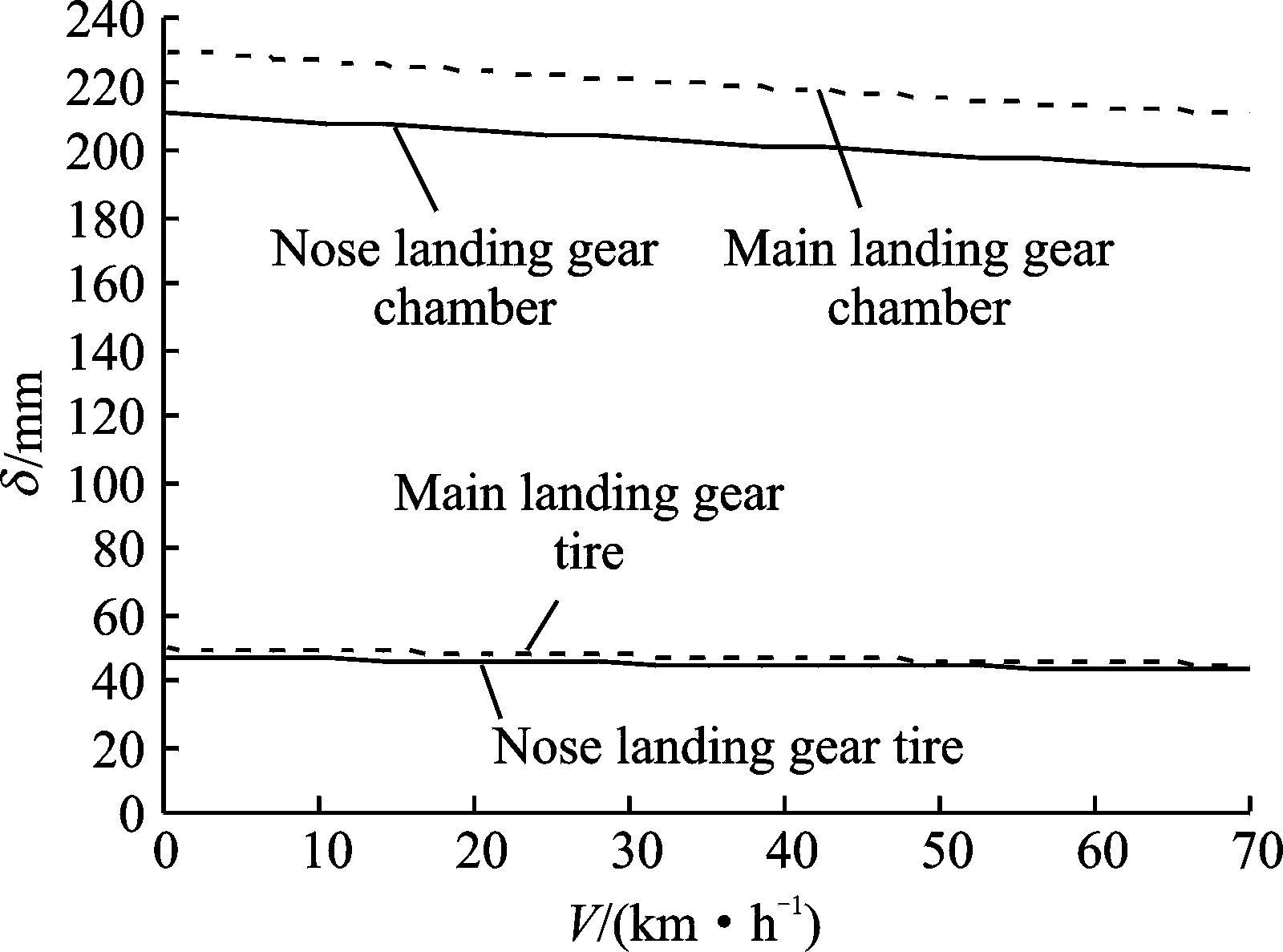
起落架缓冲支柱和轮胎的压缩量δ与其承受的载荷有关,其随速度的变化如图 4所示。可以看到,随着滑跑速度的提高,缓冲支柱和轮胎的压缩量减小,但轮胎压缩量的变化并不大。
|
图 4 缓冲支柱及轮胎压缩量随滑跑速度的变化 Figure 4 Change of deformations of chamber and tire with velocity |
2 机体侧向模态频率分析 2.1 停机状态机体侧向模态频率
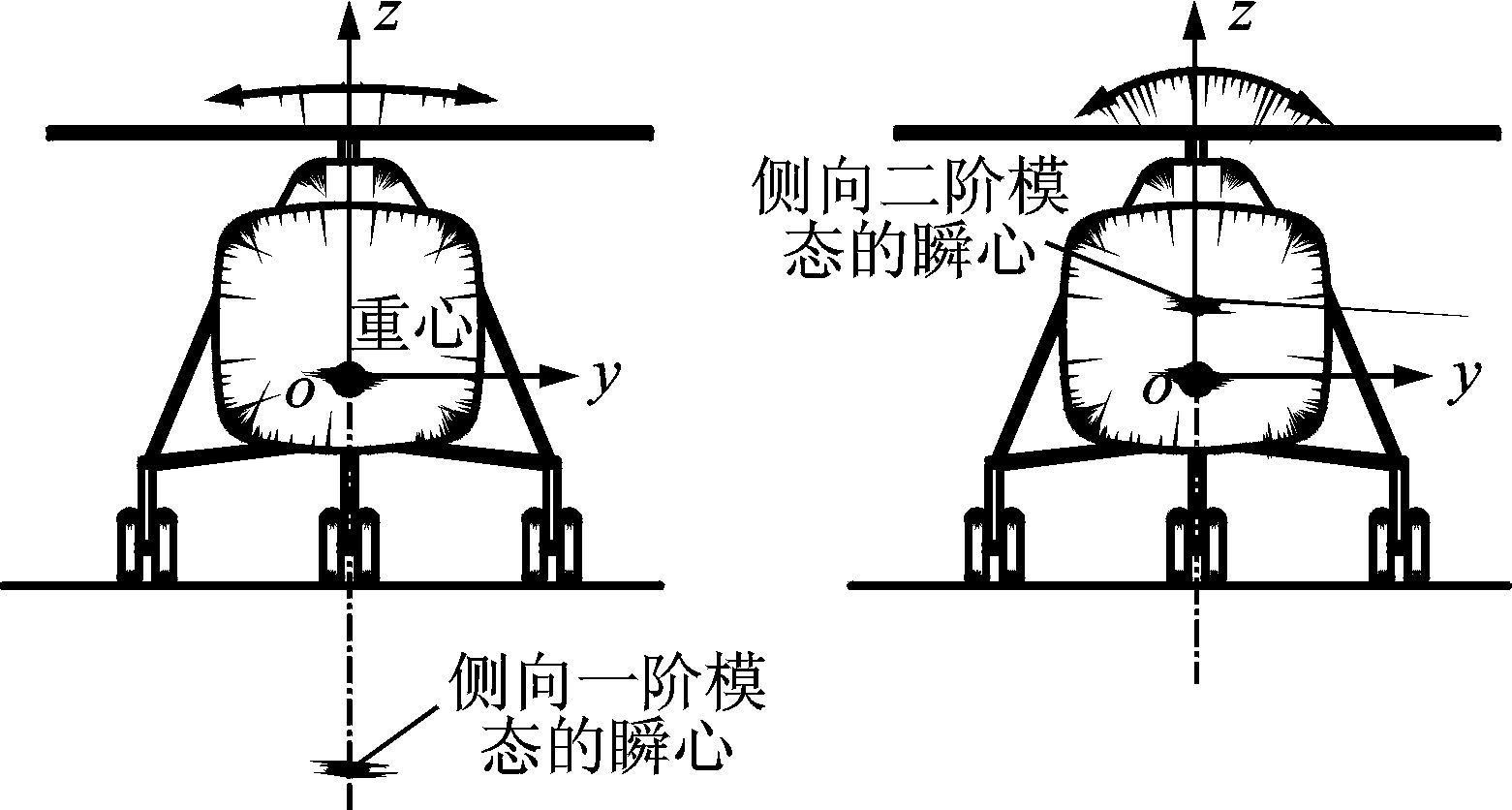
机体横向运动存在重心的侧向平移及绕质心的转动这两个自由度,如图 5所示。这两个自由度之间相互耦合,可通过坐标变换,转换为两个相互独立、绕各自瞬心转动的模态运动[9]。
|
图 5 机体侧向运动模型 Figure 5 Model of fuselage lateral motion |
严格说来,起落架缓冲支柱和轮胎的弹性力和阻尼力具有非线性特性[10],须采用非线性振动分析或数值仿真分析[11-12]。在工程设计分析中常采用小扰动假设,对起落架刚度和阻尼进行等效线性化法处理,以便于应用线性振动理论进行地面共振分析。起落架缓冲支柱和轮胎的等效刚度、等效阻尼取决于静压缩量、振动频率及振动幅值等参数,一般由试验获得[3]。第1节通过计算得到了起落架载荷及静压缩量随滑跑速度的变化曲线,若能获得各滑跑速度下的机体模态频率,则可计算起落架的等效刚度及等效阻尼。
设机体重心的侧向位移为y,绕纵轴的滚转角φx,则机体侧向平移与滚转的无阻尼自由振动方程为
| $\left\{ \begin{align} & M\ddot{y}+\left( 2{{k}_{ym}}+{{k}_{yn}} \right)y+ \\ & [2{{k}_{ym}}{{z}_{m}}+{{k}_{yn}}{{z}_{n}}]{{\varphi }_{x}}=0 \\ & {{I}_{x}}{{{\ddot{\varphi }}}_{x}}+(2{{k}_{ym}}{{z}_{m}}+{{k}_{yn}}{{z}_{n}})y+ \\ & (2{{k}_{zm}}{{y}^{2}}_{m}+2{{k}_{ym}}{{z}^{2}}_{m}+{{k}_{yn}}{{z}^{2}}_{n}){{\varphi }_{x}}=0 \\ \end{align} \right.$ | (2) |
式中:M为机体质量;Ix为机体绕纵轴的惯性矩;kyn,kym分别为前、主起落架(即轮胎)的侧向刚度;kzm为主起落架垂向等效刚度;ym为主起落架半间距;其他尺寸符号见图 1标注。
令q={yφx}T,式(2)的矩阵形式为
| $\ddot{q}+Aq=0$ | (3) |
式中系数矩阵
| $\begin{align} & {{k}_{11}}=\left( 2{{k}_{ym}}+{{k}_{yn}} \right)/M \\ & {{k}_{12}}=\left( 2{{k}_{ym}}{{z}_{m}}+{{k}_{yn}}{{z}_{n}} \right)/M \\ & {{k}_{21}}=\left( 2{{k}_{ym}}{{z}_{m}}+{{k}_{yn}}{{z}_{n}} \right)/{{I}_{x}} \\ & {{k}_{22}}=\left( 2{{k}_{zm}}y_{m}^{2}+2{{k}_{ym}}z_{m}^{2}+{{k}_{yn}}z_{n}^{2} \right]/{{I}_{x}} \\ \end{align}$ |
由于无阻尼自由振动系统表现为两个纯虚根,临界振动时,设q=q0sin(ωt+θ),代入式(3)得到特征方程为
| ${{\omega }^{4}}-({{k}_{11}}+{{k}_{22}}){{\omega }^{2}}+{{k}_{11}}{{k}_{22}}-{{k}_{12}}{{k}_{21}}=0$ | (4) |
由特征方程得到两个固有频率ω1和ω2,分别对应两个振型,从而决定了响应的两个瞬心位置。设瞬心的坐标位置为z0。因瞬心处的侧向力须为零,得到侧力平衡关系
| $M{{z}_{0}}{{{\ddot{\varphi }}}_{x}}+[2{{k}_{ym}}({{z}_{0}}+{{z}_{m}})+{{k}_{yn}}({{z}_{0}}+{{z}_{n}})]{{\varphi }_{x}}=0$ | (5) |
将两个模态运动φx1=φx10sin(ω1t+θ1)及φx2=φx20sin(ω2t+θ2)分别代入式(5),得到
| ${{z}_{01}}=\frac{{{k}_{12}}}{\omega _{1}^{2}-{{k}_{11}}}$ | (6) |
| ${{z}_{02}}=\frac{{{k}_{12}}}{\omega _{2}^{2}-{{k}_{11}}}$ | (7) |
令k11=ωx2,从式(6,7)可以看到,对于一阶模态,ω1<ωx,且两者接近,说明瞬心z01小于零(位于重心下面),是绕重心以下远处一点的转动,表现为机体的侧移模态。对于二阶模态,ω2>ωx,且两者相差较大,说明瞬心大于零(位于重心上面),是绕重心上面靠近重心一点的转动,表现为机体的滚转模态,如图 5所示。
得到机体侧向一、二阶模态的固有频率和瞬心位置后,就可以确定各个模态的质量、刚度。对应各个模态的机体质量分别为Ix1=Ix+Mz012和Ix2=Ix+Mz022,模态刚度分别为kx1=Ix1ω12和kx2=Ix2ω22,进而可确定各个模态阻尼为
| ${{c}_{x1}}=2{{c}_{zm}}{{y}_{m}}^{2}+2{{c}_{ym}}{{({{z}_{01}}+{{z}_{m}})}^{2}}+{{c}_{yn}}{{({{z}_{01}}+{{z}_{n}})}^{2}}$ | (8) |
| ${{c}_{x2}}=2{{c}_{zm}}{{y}^{2}}_{m}+2{{c}_{ym}}{{({{z}_{02}}+{{z}_{m}})}^{2}}+{{c}_{yn}}{{({{z}_{02}}+{{z}_{n}})}^{2}}$ | (9) |
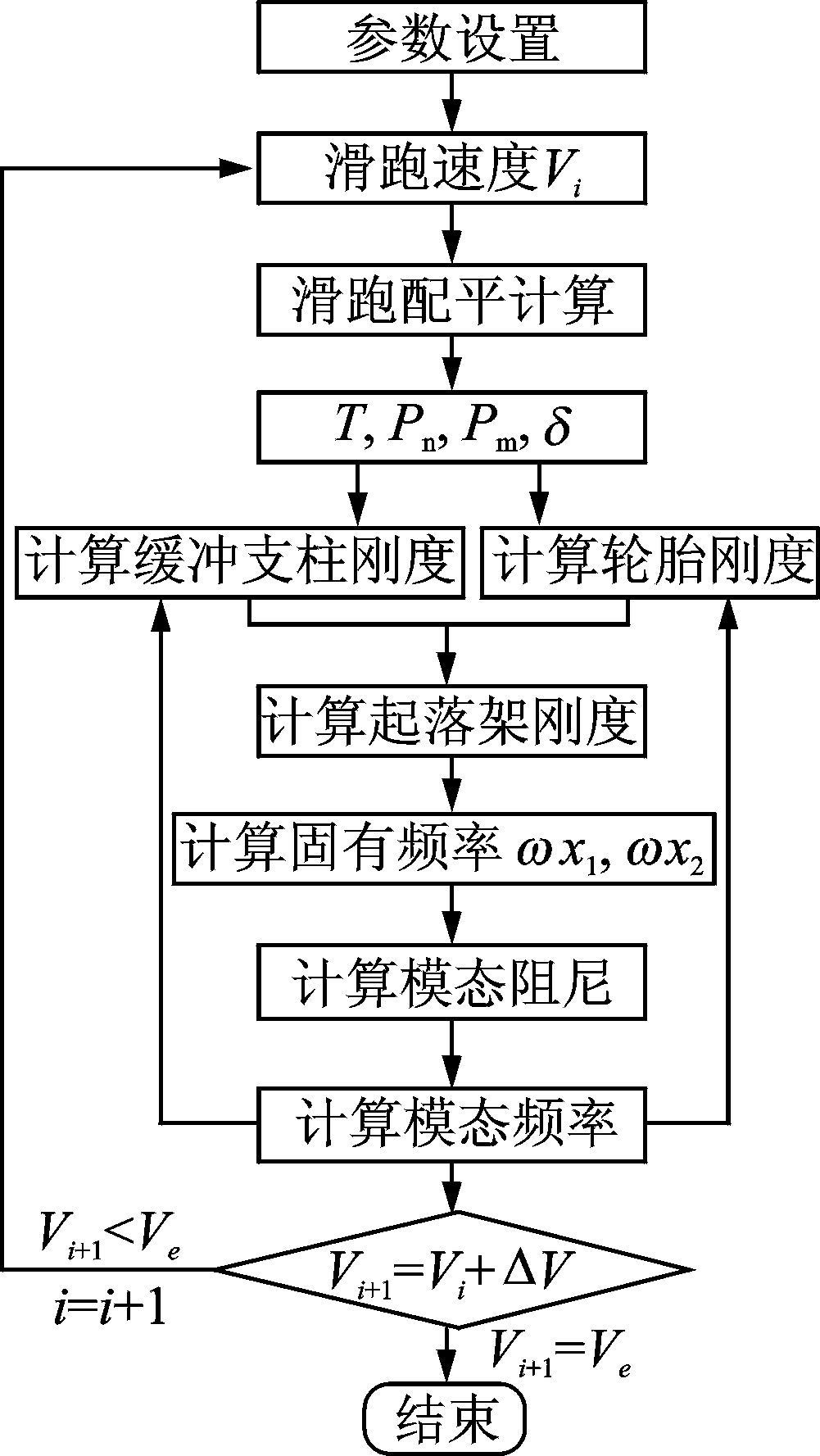
根据式(4)计算得到的是无阻尼系统的模态固有频率,与实际有阻尼系统的模态频率有一定误差。按固有频率计算得到的模态质量、模态刚度及模态阻尼也与实际情况存在一定误差。可以根据式(8,9)计算得到的模态阻尼对模态频率进行修正,然后再以修正后的模态频率计算模态质量、模态刚度及模态阻尼。若需要进一步提高模态值精度,可进行多次迭代修正。计算流程如图 6所示。
|
图 6 计算流程 Figure 6 Calculation program |
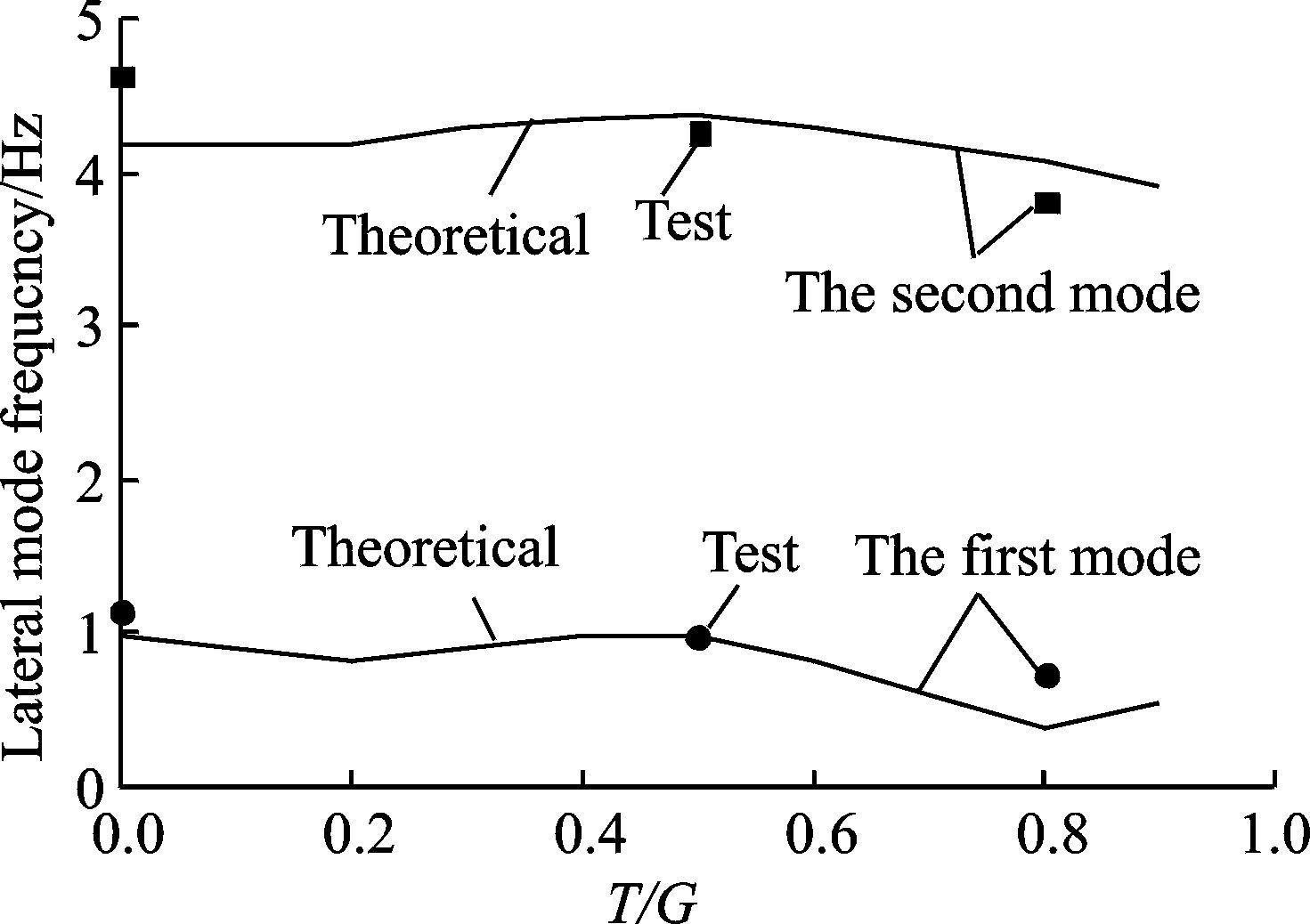
直升机最大设计重量时,在不滑跑的情况下,机体在起落架上的侧向一阶、二阶模态频率随拉力重量比的变化曲线如图 7所示,图中一并显示了试验数据以便进行比较。从图 7可以看到,对于最危险的机体侧向二阶模态,低拉力状态时模态频率理论值低于试验值,误差约为9.5%。T/G分别为50%和80%时,误差分别为2.4%和6.8%。考虑到分散性和模型精度,这个误差在工程上是可以接受的[13]。
|
图 7 机体侧向模态频率随T/G的变化 Figure 7 Change of fuselage lateral mode frequency with T/G |
2.2 滑跑状态机体侧向模态频率
直升机滑跑速度会影响机轮的侧向刚度,对机轮垂向和纵向的动力学特性几乎没有影响。因此滑跑速度主要影响机体横、侧向的固有特性。文献[5]建议,机轮侧向刚度、阻尼与滑跑速度可采用以下近似关系
| $k_{y}^{'}={{k}_{y}}\frac{1}{1+{{\left( V/r\omega \right)}^{2}}}$ | (10) |
| $c_{y}^{'}={{c}_{y}}\frac{V/r\omega }{1+{{\left( V/r\omega \right)}^{2}}}$ | (11) |
式中:V为滑跑速度;ky,cy分别为不滑跑时的机轮侧向刚度和阻尼;ω为侧向振动频率,即为直升机滑跑时机体侧向一阶或二阶模态频率;r为无载荷时的机轮半径。式(10,11)反映出,随着滑跑速度的提高,机轮的侧向刚度降低,而侧向阻尼增加。
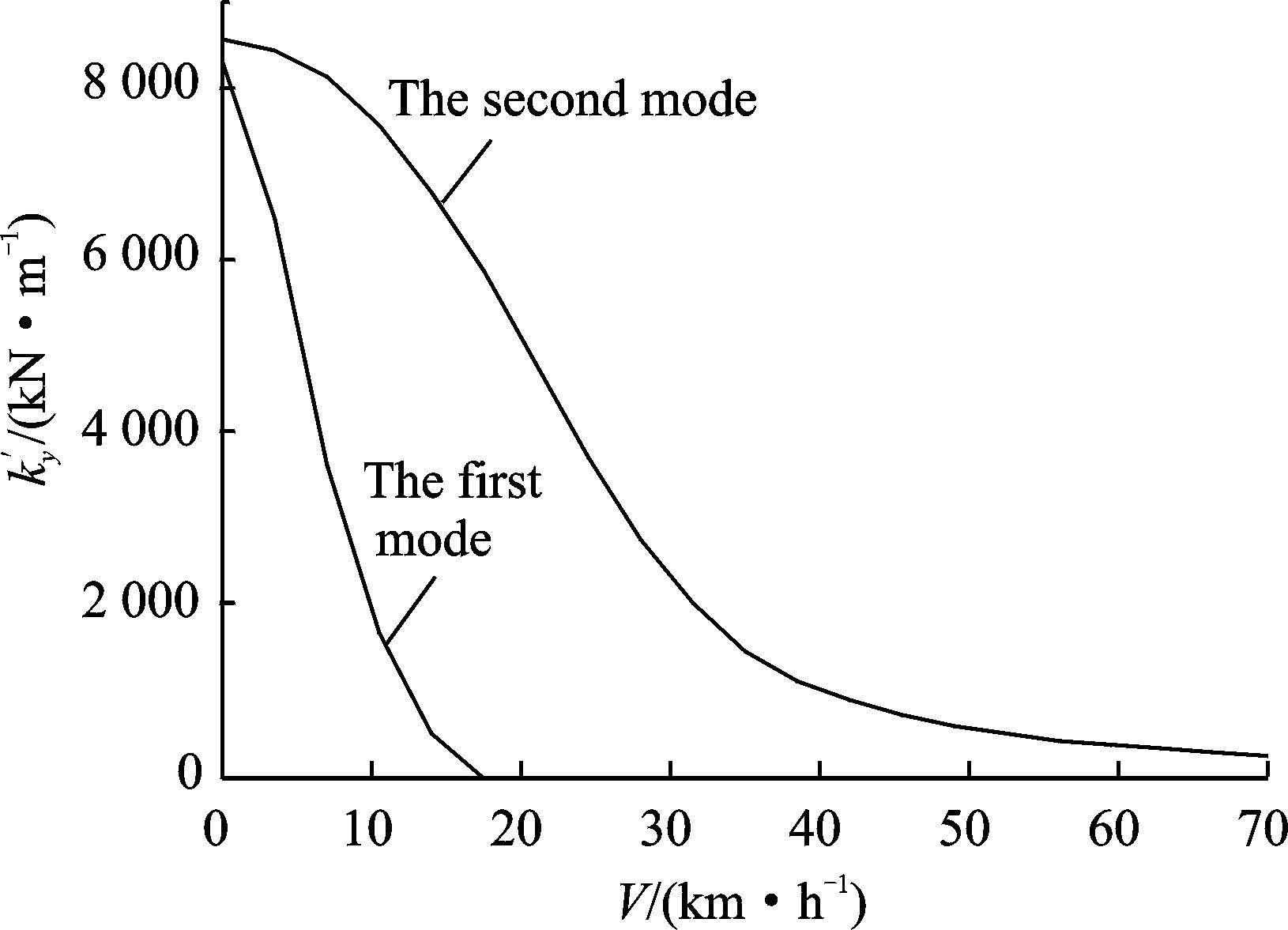
由于起落架的机轮和缓冲支柱具有非线性特性,对应机体各阶模态频率的振动,机轮及缓冲支柱具有不同的刚度和阻尼。而机体各阶模态的频率又与机轮及缓冲支柱的刚度和阻尼有关,故须通过迭代求解机轮及缓冲支柱刚度、阻尼及机体的各阶模态频率。按照图 6所示的计算流程进行迭代计算,可得到起落架机轮及缓冲支柱刚度、阻尼及机体侧向模态频率随滑跑速度的变化曲线。图 8表示以机体侧向一阶、二阶模态频率振动时机轮侧向刚度k′y随滑跑速度的变化。
|
图 8 主起落架机轮侧向刚度随滑跑速度的变化 Figure 8 Change of lateral stiffness of main landing gear with velocity |
由图 8曲线看到,以机体侧向一阶模态频率振动时,机轮的侧向刚度随滑跑速度急剧下降,在速度17 km/h左右降至零。以二阶模态频率振动时,滑跑速度10~30 km/h范围内,机轮侧向刚度迅速下降,速度超过35 km/h后刚度下降趋缓。
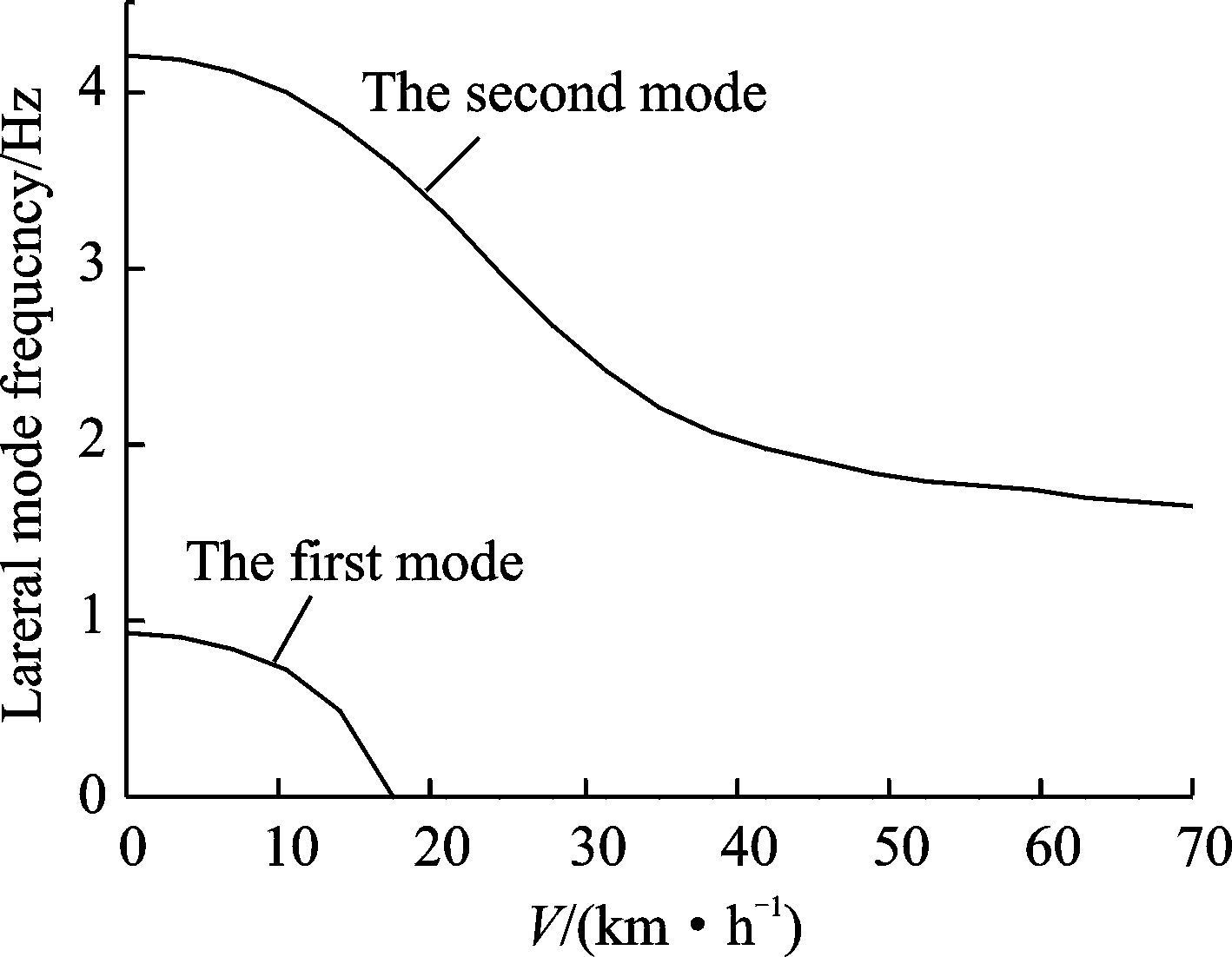
图 9表示在最大质量(13 000 kg)条件下,机体侧向一阶、二阶模态频率随滑跑速度的变化曲线。从图 9看到,机体侧向二阶模态频率随滑跑速度的提高而下降。并且在低速滑跑阶段,模态频率下降非常剧烈,滑跑速度超过35 km/h后,模态频率下降趋缓。从静止状态到滑跑速度35 km/h,侧向二阶模态频率从4.2 Hz降到2.2 Hz左右,模态频率的降幅达47.6%。
|
图 9 机体侧向模态频率随滑跑速度的变化 Figure 9 Change of fuselage lateral mode frequency with velocity |
比较图 8,9曲线可以看到,机体侧向二阶模态频率随滑跑速度的变化趋势与机轮侧向刚度的变化趋势非常接近,说明机轮侧向刚度的降低是导致机体侧向二阶模态频率降低的主要影响因素。滑跑速度提高会降低机体侧向二阶模态频率,从而降低机体与摆振后退型耦合的共振转速,使不稳定区向低转速移动。一旦不稳定区边界的旋翼转速低于工作转速,那么在有颠簸或扰动情况时就会发生地面共振。
机体侧向一阶模态频率随滑跑速度迅速下降(见图 9),并在速度17 km/h 左右时趋于零,接近于机轮侧向刚度为零这种极端情况下的机体侧移模态(零频模态)。因滑跑时机体侧向一阶模态的频率比停机状态时更低,其与摆振后退型耦合的共振转速也就更低。因此与停机状态相比,直升机滑跑时机体侧向一阶模态更不具有产生动不稳定的可能性,在滑跑地面共振分析中可不予重点关注。
3 结束语针对直升机仅由总距操纵实现地面稳定滑跑的状态,分析了旋翼拉力、地面滑跑载荷、机轮侧向刚度及机体侧向高阶模态频率等参数随滑跑速度的变化规律。结果发现,机轮侧向刚度随滑跑速度的降低,是造成机体侧向高阶模态频率降低的关键因素。尤其在低速滑跑阶段,随着速度的提高,机体侧向二阶模态频率急剧下降,使直升机产生滑跑地面共振的潜在风险。
| [1] | 国防科学技术工业委员会.GJB720.5—89.军用直升机强度和刚度规范:振动?机械及气动弹性不稳定性[S]. 北京: 国防科学技术工业委员会, 1989. |
| [2] | 张晓谷. 直升机地面共振设计[M]. 北京: 航空工业出版社, 1995 . |
| [3] | 航空航天工业部科学技术研究院. 直升机动力学手册[M]. 北京: 航空工业出版社, 1991 . |
| [4] |
许勤勇, 殷士辉, 徐玉貌.
直升机地面滑跑飞行力学研究[J]. 直升机技术 , 2015 (2) : 6–10.
Xu Qinyong, Yin Shihui, Xu Yumao. Flight dynamic analysis of helicopter taxiing[J]. Helicopter Technique , 2015 (2) : 6–10. |
| [5] | 米里. 直升机计算和设计(第二卷):振动和动强度[M]. 北京: 国防工业出版社, 1976 . |
| [6] | 诸德培. 摆振理论及防摆措施[M]. 北京: 国防工业出版社, 1984 . |
| [7] |
胡国才, 刘湘一, 刘书岩, 等.
舰面状态直升机机体在起落架上的固有频率分析[J]. 海军航空工程学院学报 , 2012, 27 (6) : 639–644.
Hu Guocai, Liu Xiangyi, Liu Shuyan, et al. Analysis of helicopter natural frequencies on landing gear at ship-borne conditions[J]. Journal of Naval Aeronautical Engineering Institute , 2012, 27 (6) : 639–644. |
| [8] | Currey N S. Aircraft landing gear design: Principles and practices[M]. USA: AIAA, 1988 . |
| [9] |
张晓谷, 刘强.
复数坐标及互激励分析在直升机“地面共振"分析中的应用[J]. 航空学报 , 1992, 13 (11) : 586–593.
Zhang Xiaogu, Liu Qiang. The application of complex coordinates and mutual excitation analysis to the investigation of helicopter ground resonance[J]. Acta Aeronautica et Astronautica Sinica , 1992, 13 (11) : 586–593. |
| [10] |
胡国才, 陈军民.
直升机起落架双腔式缓冲支柱动刚度研究[J]. 海军航空工程学院学报 , 2007, 22 (6) : 601–604.
Hu Guocai, Chen Junmin. Research on dynamic stiffness of bi-chambered shock-absorber of helicopter landing gear[J]. Journal of Naval Aeronautical Engineering Institute , 2007, 22 (6) : 601–604. |
| [11] | Tongue B H, Flowers G T. Non-linear rotorcraft analysis[J]. International Journal of Non-linear Mechanics , 1988, 23 (3) : 189–203. DOI:10.1016/0020-7462(88)90011-X |
| [12] |
胡国才, 崔坤林, 刘湘一.
地面系留对直升机动力响应的影响研究[J]. 航空学报 , 2008, 29 (1) : 387–392.
Hu Guocai, Cui Kunlin, Liu Xiangyi. Ground mooring effects on helicopter dynamic response[J]. Acta Aeronautica et Astronautica Sinica , 2008, 29 (1) : 387–392. |
| [13] | Voronkov A Z, Triphonova N A. Coaxial helicopter safety from ground resonance point of view[C]//The 21st European Rotorcraft Forum.Saint-Petersburg,Russia:[s.n.],1995:1-13. |
 2016, Vol. 48
2016, Vol. 48


