2. 中国空气动力研究与发展中心高速空气动力研究所,绵阳,621000
2. High Speed Aerodynamic Institute, China Aerodynamics Research & Development Center, Mianyang, 621000, China
飞翼布局是仅由单独翼面构成的气动布局形式,具有优良的气动、隐身性能,特别是小展弦比飞翼布局,具有良好的跨、超音速气动特性,是下一代超音速战斗机优先选择的布局方式之一[1]。
对于大后掠三角翼的研究表明[2-3],在不大的迎角下,三角翼背风面会产生一对稳定的前缘涡,该涡在背风面诱导出很强的附加升力,即前缘涡升力。随着迎角的增大,前缘涡逐渐增强,涡升力逐渐增大,提高了飞机的失速迎角,增强了飞机的机动性。随着迎角的继续增大,前缘涡将出现涡破裂,导致涡升力减小,全机失速。
在跨音速情况下,激波的出现将导致激波/边界层干扰、激波/前缘涡干扰等更为复杂流动现象,呈现出许多与亚音速不同的流动特点[4-6]。针对激波/前缘涡干扰的流动机理,NASA 兰利研究中心和与之对应的第二次“国际涡流实验”(VFE-2)进行了大量的试验和数值模拟研究[7-11]。结果表明,与亚声速时涡破裂位置随着迎角的增加而逐渐向上游移动不同,跨音速时激波将穿过前缘涡,导致前缘涡破裂,涡破裂位置在很小迎角范围内由后缘突然前移30%弦长,导致全机失速,俯仰力矩急剧上仰。随着迎角继续增大,涡破裂位置缓慢前移。
杨永等[12]对第二次涡流试验中的尖前缘三角翼模型的研究表明,在支架前端和尾部存在多道激波,且支架前激波与主涡发生了干扰。中等迎角下激波的干扰作用没有导致前缘涡破裂;临界迎角时,支架附近激波经过前缘涡,主涡发生了破裂,使得涡破裂位置突然向上游移动弦长的30%之多,全机失速;随着迎角继续增大,涡破裂位置则缓慢前移。
目前,中国也建立了65°后掠角、单前缘和W形后缘的小展弦比飞翼标准模型,并开展该飞翼布局典型跨音速气动、流动特性研究[13-14]。研究表明,跨声速时,在相同迎角条件下,厚飞翼布局上翼面激波位置较薄飞翼布局更为靠前,涡破裂迎角发生较早,薄飞翼布局较厚飞翼布局失速迎角推迟约8°。
本文采用数值模拟方法,研究了跨音速巡航马赫数下(Ma=0.9),小展弦比飞翼模型的流动特性,并分析了翼身厚度对全机流动特性,特别是前缘涡流动的影响,为大后掠飞翼布局气动布局设计和流动机理分析提供基础。
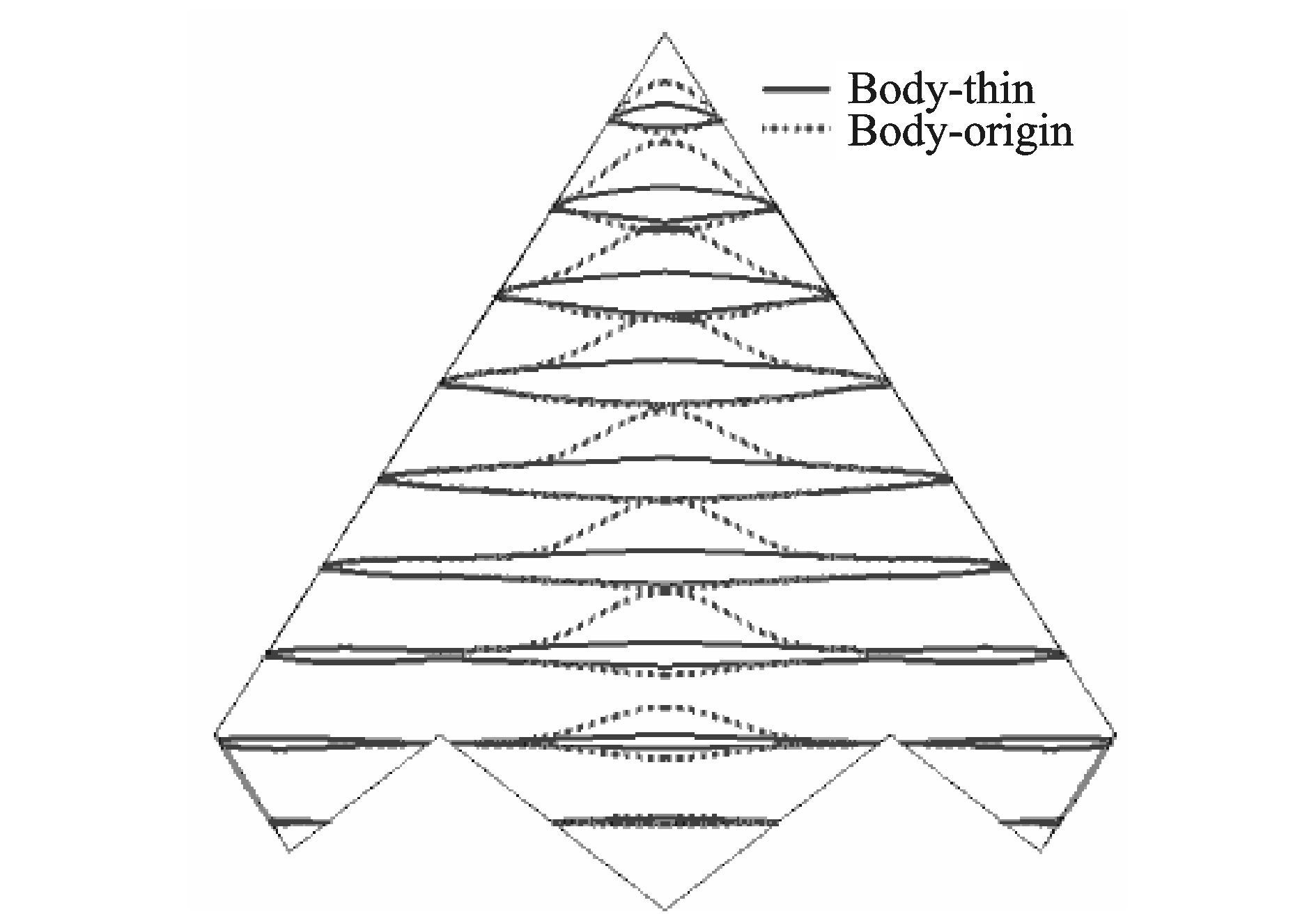
1 计算模型及数值计算方法 1.1 计算模型本文的计算模型为中国建立的小展弦比飞翼布局标准模型,外形如图 1所示。该模型前缘后掠角65°,W型后缘后掠角±47°,展弦比1.54,对称面处翼型厚度10.0%,外翼翼型厚度5.0%。采用变前缘半径设计。力矩参考点位于0.45机身长度处。
|
图 1 两种翼身厚度典型剖面形状对比 Figure 1 Typical slices of two configurations |
在小展弦比飞翼模型基础上,保持机翼不变,降低翼身厚度,形成薄飞翼布局模型,模型对称面翼型最大厚度为4.0%。小展弦比飞翼布局薄厚模型各弦向剖面如图 1所示。
1.2 数值模拟方法及网格采用有限体积法对复杂外形绕流进行数值模拟,控制方程采用雷诺平均N-S方程组,空间离散方法为有限体积法,无粘通量项采用二阶精度的Roe通量差分分裂格式,粘性项采用二阶精度的中心差分格式,时间推进采用隐式LU-SGS方法求解。湍流模型是两方程k-ω SST模型。为了加快收敛速度,采用了多重网格技术。
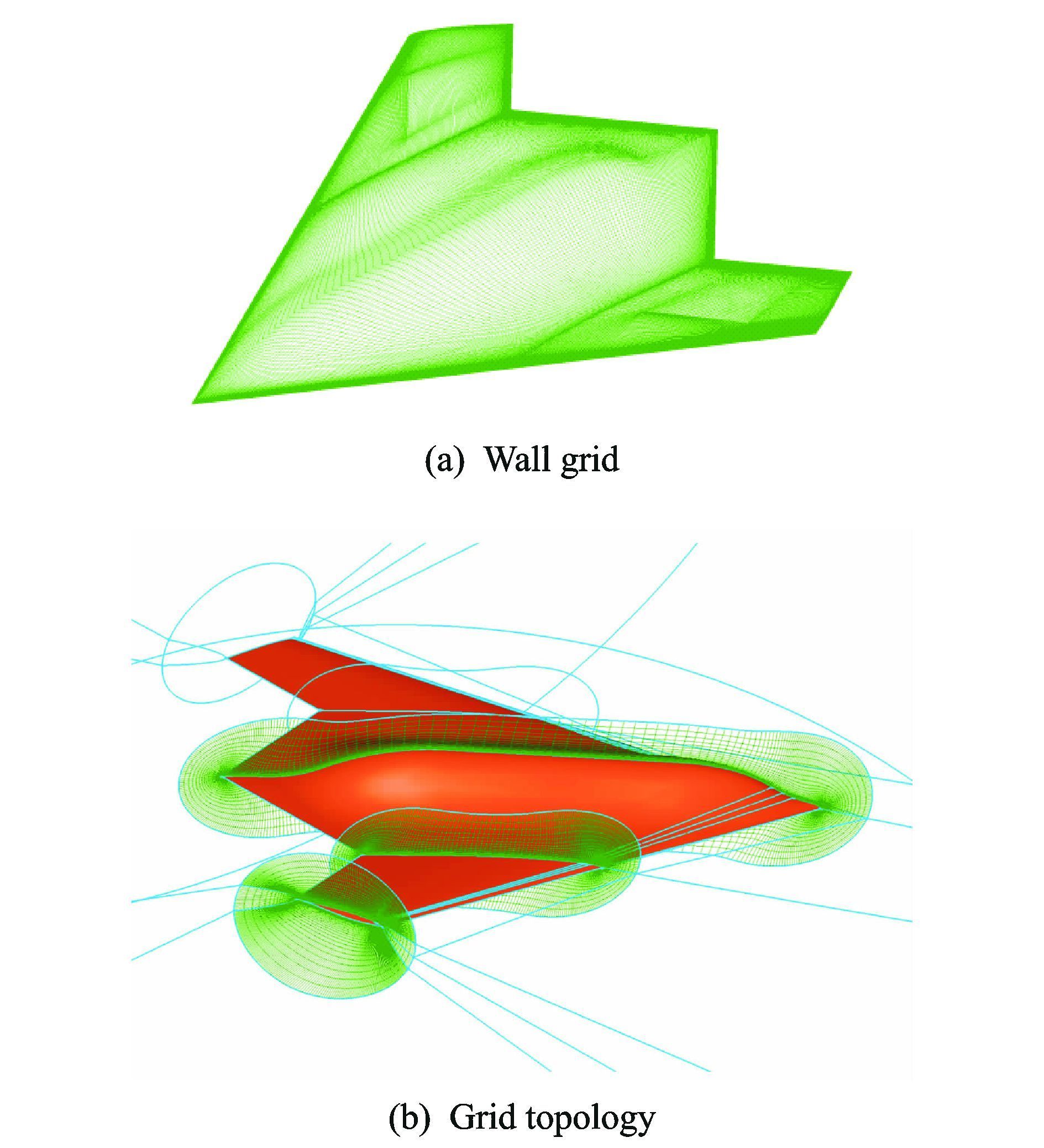
计算网格采用多块对接结构网格,空间均采用“O”型网格,物面均采用“H” 型网格,网格数量约800万个,附面层第一层网格y+≈1。小展弦比飞翼布局模型计算模型表面网格和空间拓扑结构如 图 2所示。物面采用无滑移无穿透边界条件,远场采用无反射远场边界条件。
|
图 2 计算网格 Figure 2 Computational grid |
1.3 计算结果验证
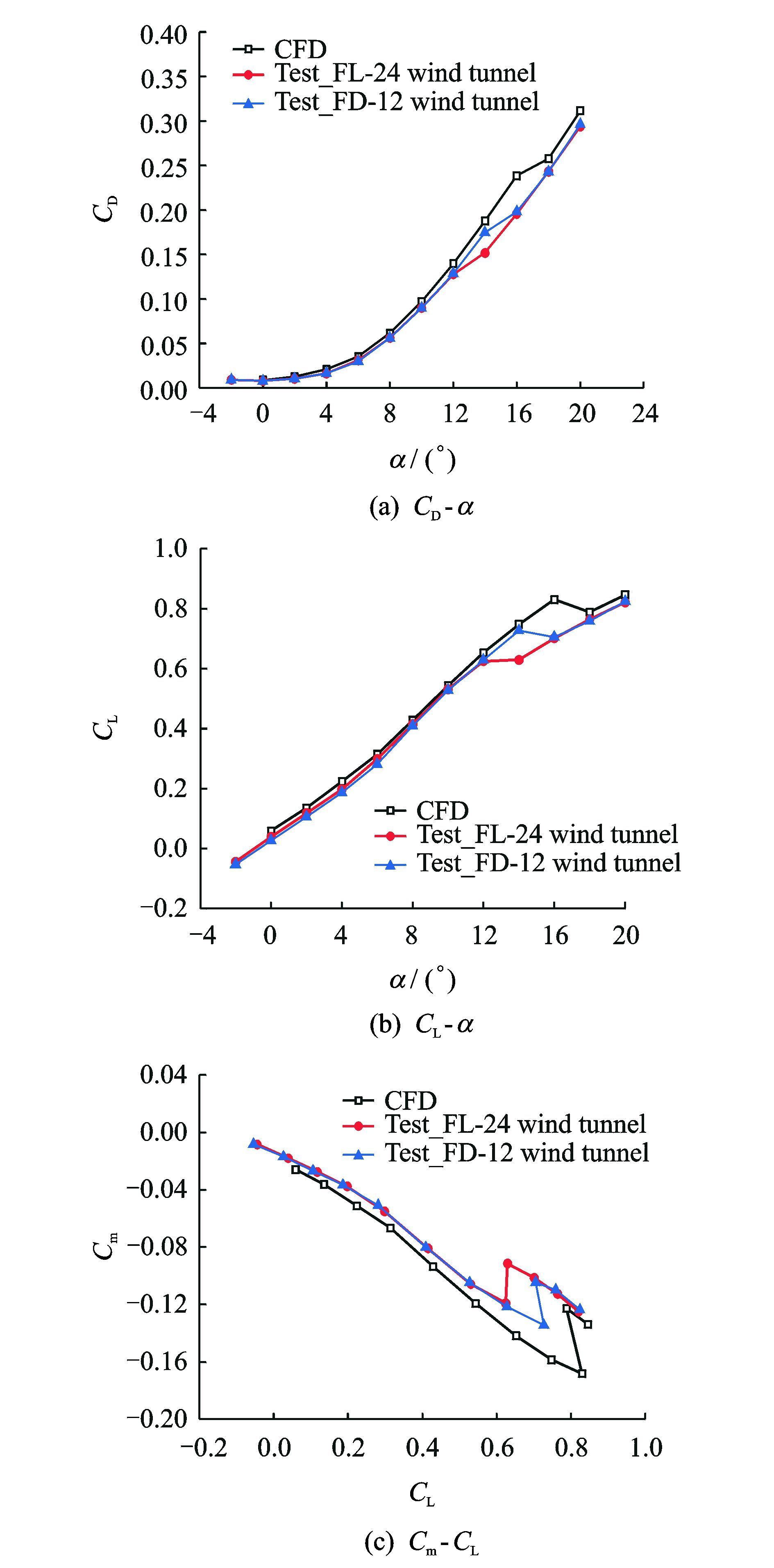
为了验证数值模拟方法和网格的可靠性,对数值模拟结果和课题组在FL-24风洞(中国空气动力研究与发展中心高速所)、FD-12风洞(中国航天空气动力技术研究院)的风洞试验结果进行了比较。图 3是当Ma=0.9、无侧滑时,小展弦比飞翼布局模型计算和试验结果比较,图中CL为升力系数,CD为阻力系数,Cm为力矩系数,α为迎角。从图 3可以看出:在中小迎角范围内,纵向气动特性的计算结果与试验结果基本一致;在失速迎角附近,计算曲线也较好地模拟出前缘涡破裂导致的升力失速和俯仰力矩上仰现象,但计算的失速迎角、可用升力系数相对于试验结果偏大。这主要是因为跨音速前缘涡破裂现象是一种十分复杂的流动现象,受来流湍流度、支架干扰和洞壁干扰等诸多因素影响,即使同一试验模型在不同的风洞进行试验也不能取得一致的结果,流动的复杂性造成了模拟结果的偏差。但总体而言,计算结果与试验结果的流动规律完全吻合,计算结果可信。
|
图 3 试验与计算结果比较(Ma=0.9) Figure 3 Comparison of test and computational results(Ma=0.9) |
1.4 数据处理
为了更为详细地分析翼身厚度变化对涡升力的影响,本文采用波尔豪森提出的前缘吸力比拟法,将升力分解为位流升力和涡升力之和,公式如下
| ${{C}_{L}}={{C}_{Lp}}+{{C}_{Lv}}$ | (1) |
式中:CLp表示位流升力系数;CLv表示涡升力系数。由于飞翼标模的截面翼型具有弯度,0°迎角时升力不为0,因此对波尔豪森提出的升力分解公式作了部分修正,增加了一个表示0°迎角升力系数的常数项CL0,使其更加适应于飞翼标模涡升力问题的讨论。
位流升力系数的计算公式为
| $~{{C}_{Lp}}={{K}_{p}}sin\alpha \cdot co{{s}^{2}}\alpha +{{C}_{L0}}$ | (2) |
涡升力系数表达式则沿用经典前缘吸力比拟法的结果为
| ${{C}_{Lv}}={{K}_{v}}cos\alpha \cdot si{{n}^{2}}\alpha $ | (3) |
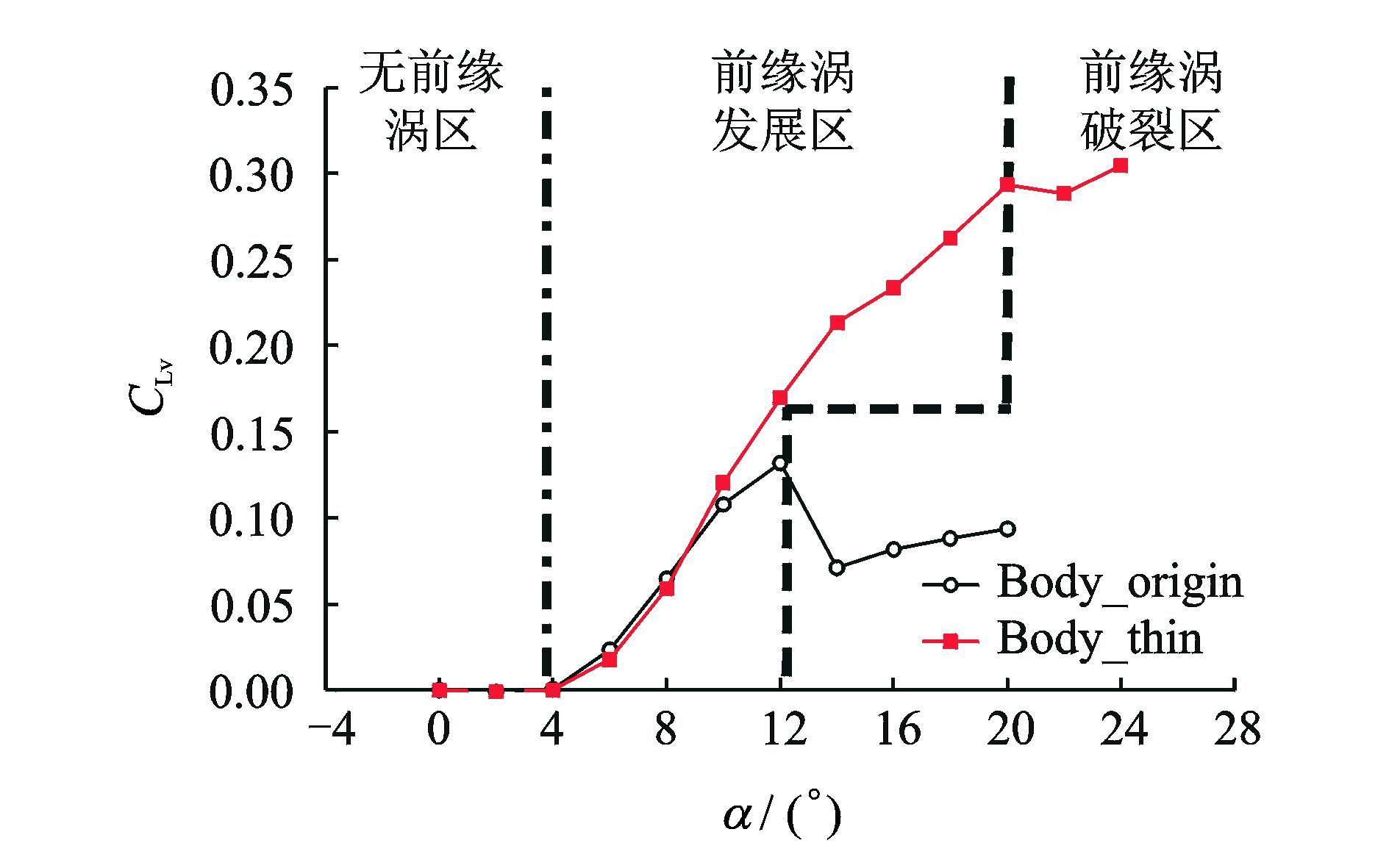
本文首先对有薄厚飞翼模型的跨音速涡升力特性进行了比较。图 4是当Ma=0.9时,薄厚飞翼布局模型涡升力系数随迎角的变化曲线。根据前缘涡升力随迎角的变化规律以及前缘涡流动随迎角的演化过程,将其划分为3个区域,分别是无前缘涡区、前缘涡发展区和前缘涡破裂区。从中可以看出,在无前缘涡区(α≤4°),涡升力系数基本为零,即流场无前缘涡作用,全机流动以附着流动为主;在前缘涡发展区(迎角范围为4°到失速迎角),涡升力系数逐渐增大,即全机出现前缘涡流动,并随迎角的增大逐渐发展壮大,且薄厚飞翼模型涡升力系数基本相同,同时翼身厚度的增大导致该区域迎角范围减小;在前缘涡破裂区(失速迎角之后),失速迎角附近,涡升力系数先减小后逐渐增大,即前缘涡发生破裂,翼身厚度的存在将导致涡破裂迎角大幅提前,前缘涡发展区迎角范围大幅减小。以下将结合小展弦比薄厚飞翼模型流场结构,揭示不同区域内翼身厚度对小展弦比飞翼布局气动、流动特性影响。
|
图 4 薄厚飞翼模型涡升力系数曲线比较(Ma=0.9) Figure 4 Effect of wing-body thickness on vortex lift(Ma=0.9) |
2.2 无前缘涡区
对于该区域,薄厚飞翼模型背风面流动以附着流动为主,涡升力基本为零。
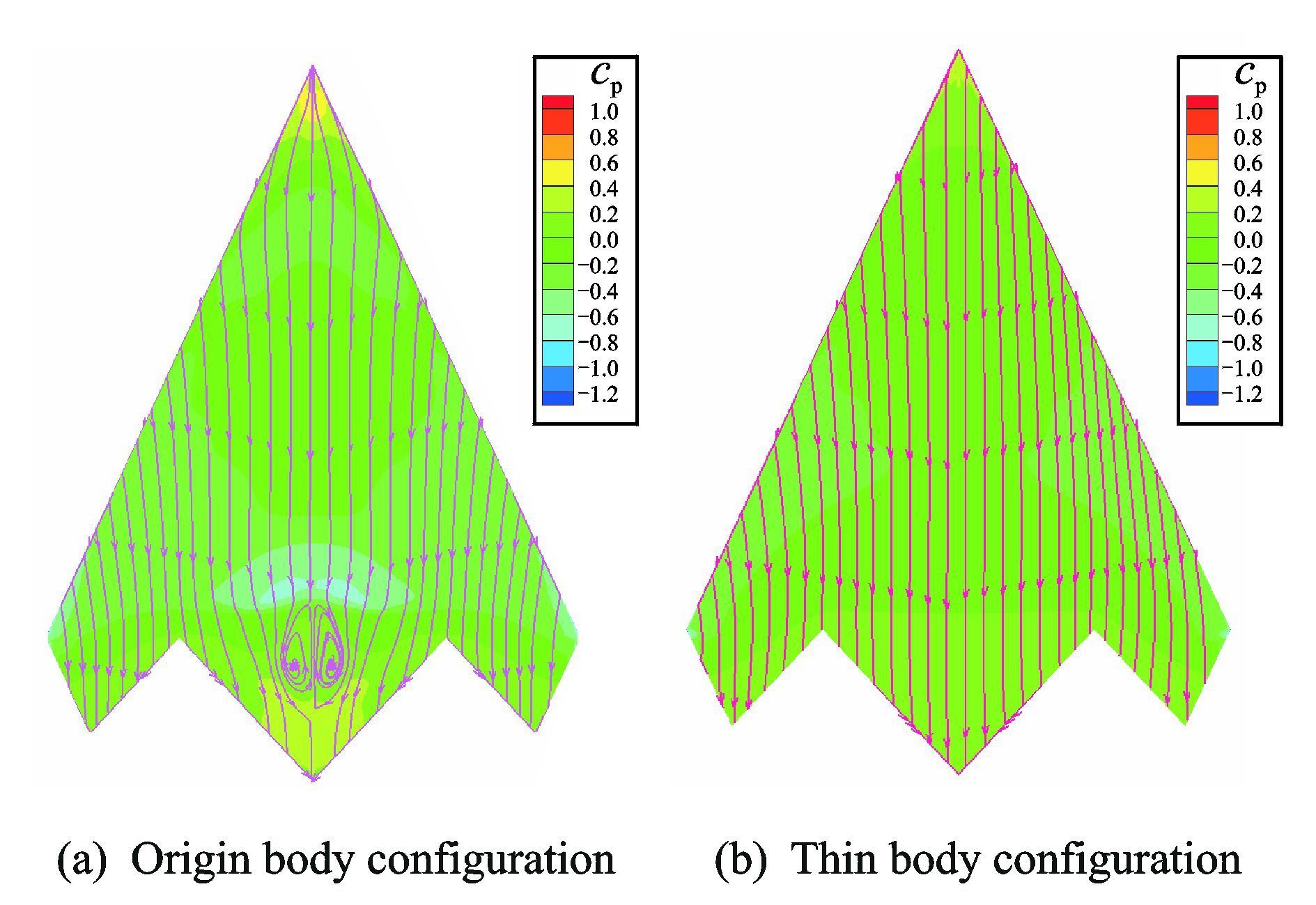
图 5是当Ma=0.9,α=2°时,薄厚飞翼模型背风侧压力云图。从中可以看出,此时背风侧均以附着流动为主。在机头附近,较大的翼身厚度将导致明显的展向流动,使流线向翼尖方向倾斜,引起显著的侧洗作用;在尾部收缩处,较大的翼身厚度将使该处出现一对螺旋点,导致该区域流动出现分流。这主要是由于翼身厚度较大,尾部收缩较快,导致气动绕过尾部收缩处后产生了很大的纵向逆压梯度和横向逆压梯度,诱导边界层出现螺旋形分离流动。尾部流动的分离将导致全机阻力增大,因此,在飞翼布局设计中应尽量避免。
|
图 5 薄厚飞翼模型背风侧压力云图(Ma=0.9,α=2°) Figure 5 Effect of wing-body thickness on pressure coefficient distributions(Ma=0.9,α=2°) |
2.3 前缘涡发展区
对于该区域,飞翼模型背风侧出现前缘涡,随着迎角的增大逐渐发展壮大,涡升力增大,薄厚飞翼模型涡升力基本相同。
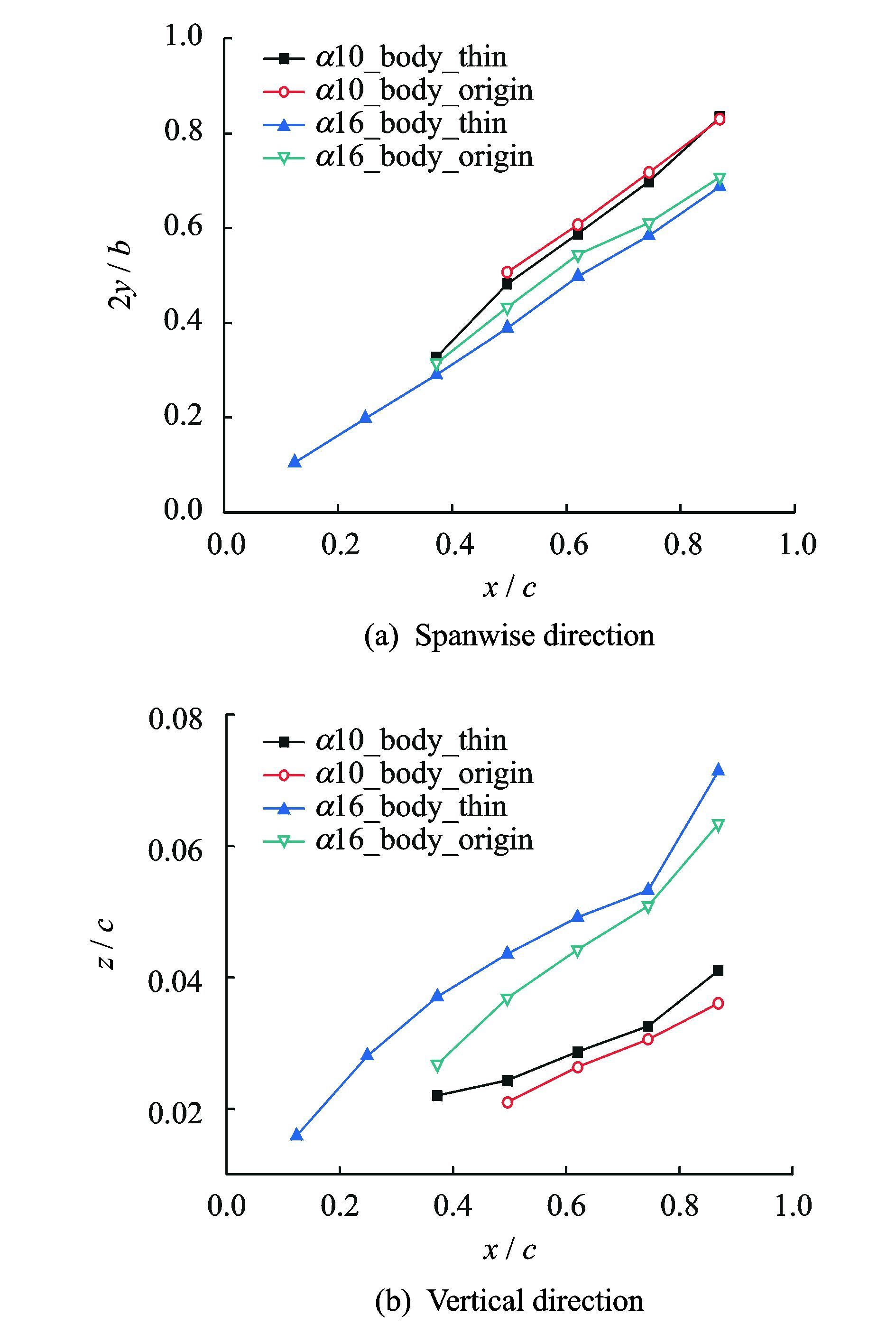
为了分析机身厚度对前缘涡发展的影响,本文比较了薄厚飞翼模型前缘涡涡核的空间位置。涡核位置为前缘涡各截面涡量值最大点位置。图 6是当Ma=0.9时,薄厚飞翼模型前缘涡涡核空间位置沿弦向的变化曲线。从中可以看出,翼身厚度使前缘涡的形成较晚,且其侧洗作用使前缘涡在展向上向翼尖方向平移,垂向上涡位相对较低,但其在垂向上的发展速度相对较快,其涡核与物面所呈角度更大。随着迎角的增大,翼身的侧洗作用增强。
|
图 6 薄厚飞翼模型前缘涡涡核位置变化曲线(Ma=0.9) Figure 6 Effect of wing-body thickness on vortex core position(Ma=0.9) |
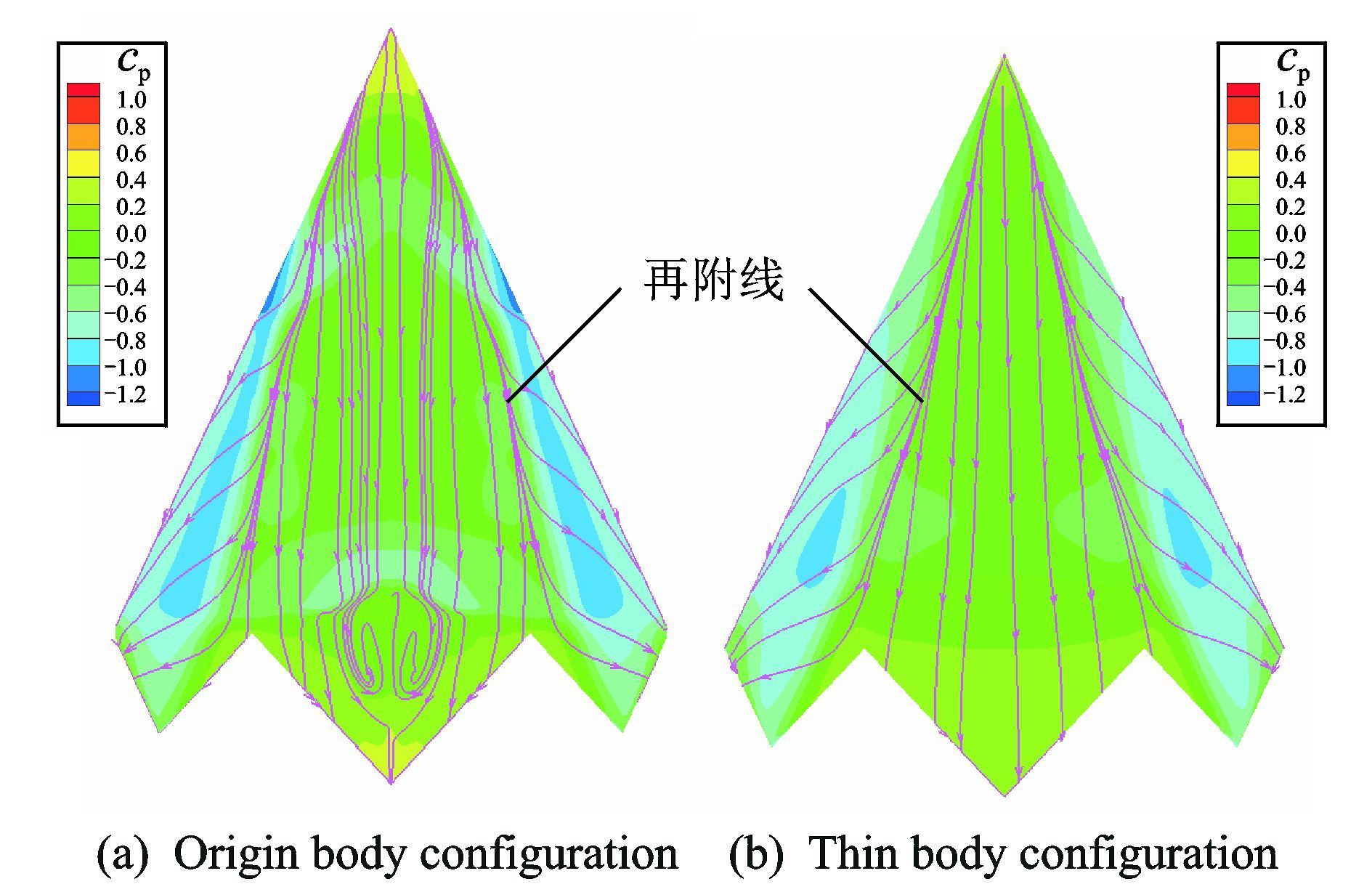
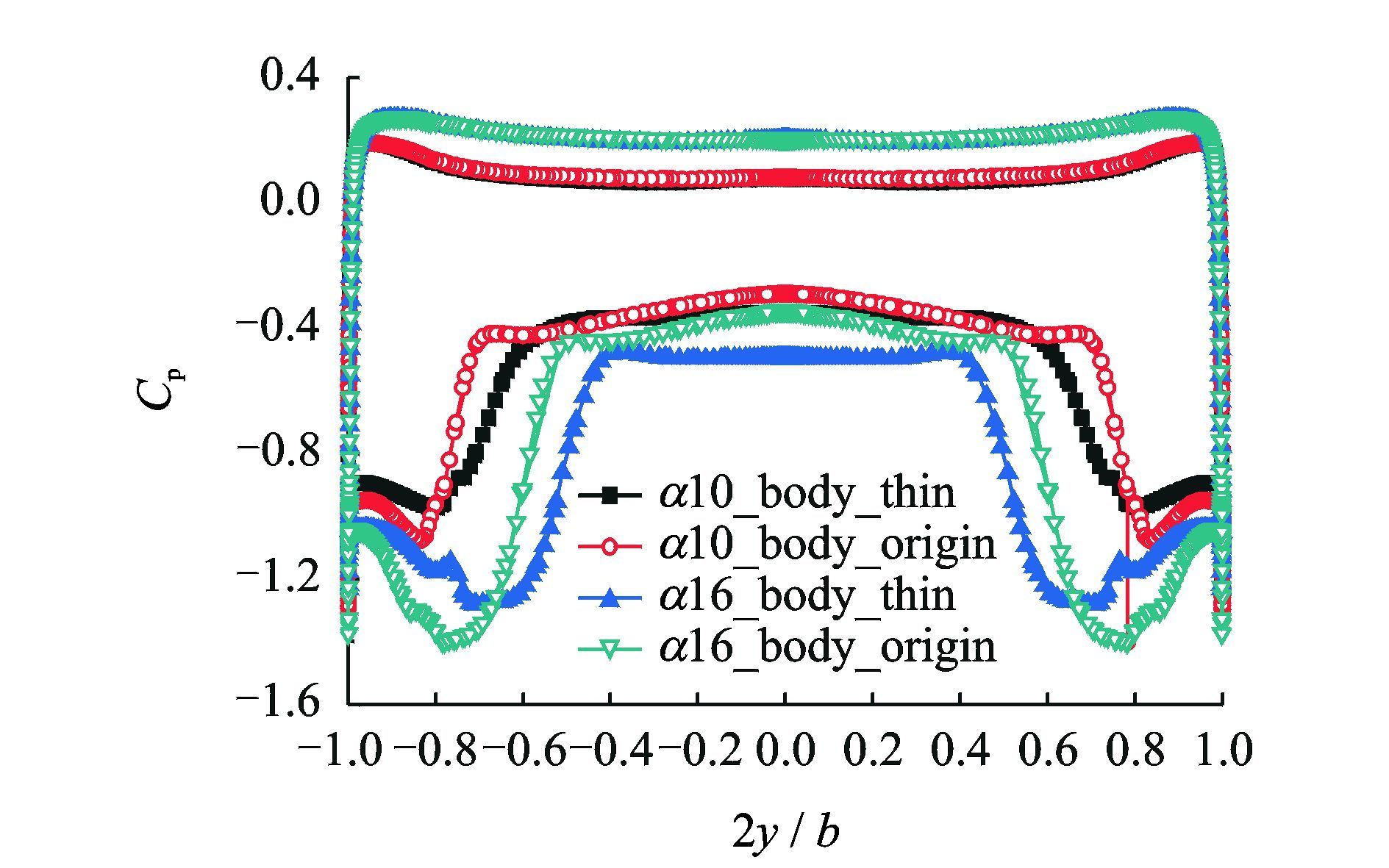
图 7是当Ma=0.9时,薄厚飞翼模型背风面的油流图和压力云图。图 8是薄厚飞翼模型x/c=0.5截面压力分布比较。从中可以看出,翼身的侧洗作用使前缘涡在机头处不能形成,导致前缘涡的形成较晚,再附线向翼尖方向移动,从而使前缘涡影响区域较小。但由于前缘涡强度增大,在物面上诱导的吸力增大,从而使得前缘涡涡升力系数基本不变。
|
图 7 薄厚飞翼模型背风侧压力云图(Ma=0.9,α=10°) Figure 7 Effect of wing-body thickness on pressure coefficient distributions(Ma=0.9,α=10°) |
|
图 8 薄厚飞翼模型x/c=0.5截面压力分布比较(Ma=0.9) Figure 8 Effect of wing-body thickness on pressure distributions in x/c=0.5(Ma=0.9) |
总之,翼身厚度的侧洗作用使飞翼模型前缘涡形成较晚,影响区域减小,但前缘涡强度增大,使得前缘涡涡升力基本不变。
2.4 前缘涡破裂区对于该流动区域,飞翼模型前缘涡发生破裂,翼身厚度导致前缘涡破裂迎角提前。
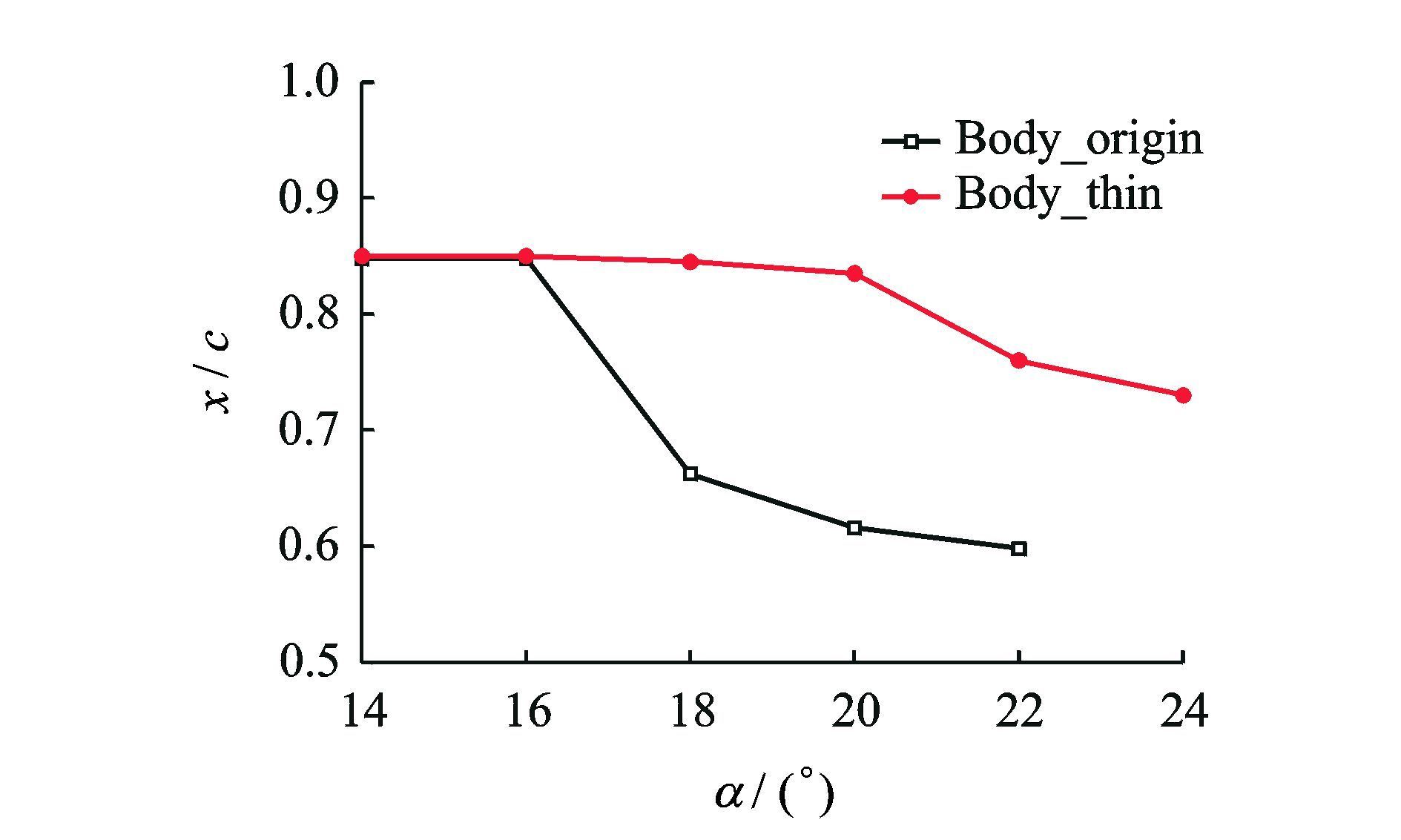
图 9是当Ma=0.9时,薄厚飞翼模型前缘涡破裂点位置随迎角的变化曲线。其中,涡破裂点位置为涡轴涡量突然下降到零处的轴向位置。从中可以看出,在失速迎角附近,前缘涡破裂点将突然由后缘大幅前移,从而导致全机涡升力大幅减小。翼身厚度将导致前缘涡破裂迎角提前4°,且破裂点前移幅度大约为薄飞翼模型时的两倍。
|
图 9 薄厚飞翼模型涡破裂点位置比较 Figure 9 Effect of wing-body thickness on vortex breakdown position |
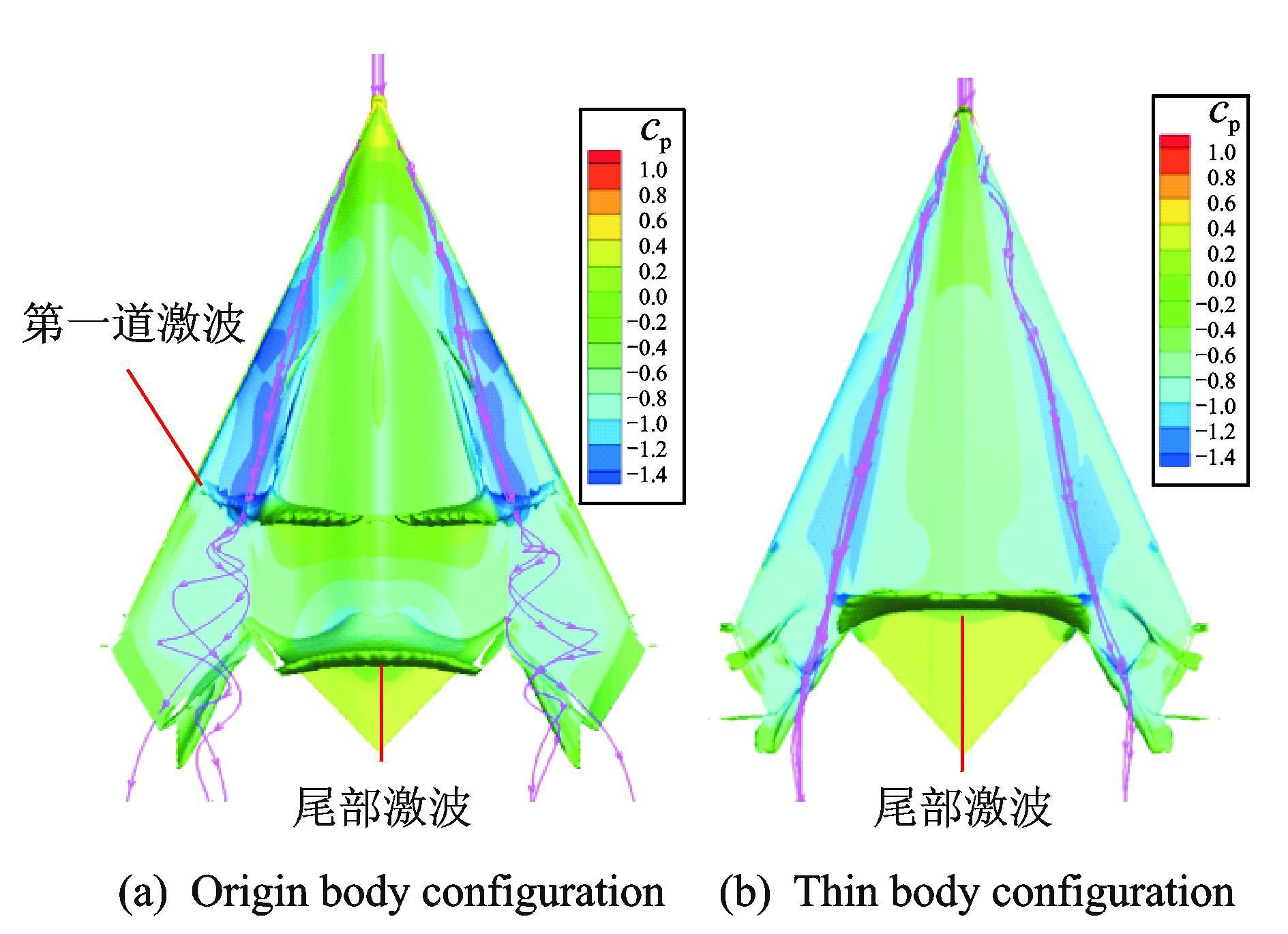
图 10是当Ma=0.9,α=18°时,薄厚飞翼模型背风侧激波面和涡轴流线图比较,其中的激波面通过密度梯度等值面表征。从图 10可以看出,飞翼布局模型背风侧存在两道激波。其中,翼身厚度在x/c=0.68处诱导出第一道激波,该激波穿过前缘涡,使前缘涡涡核轴向逆压梯度增大,诱导前缘涡发生破裂,涡破裂点由后缘突然前移到激波面。前缘涡的破裂使破裂点后区域的吸力大幅降低,涡升力大幅减小。
|
图 10 薄厚飞翼模型背风侧激波面和涡轴流线图比较(Ma=0.9,α=18°) Figure 10 Effect of wing-body thickness on shock wave surface and streamline in vortex axial line (Ma=0.9,α=18°) |
对于尾部激波,与薄厚度模型相比,大厚度飞翼模型激波强度减小,位置略有后移。虽然,薄厚度模型尾部激波同样穿过了前缘涡,前缘涡轴向速度也有所降低,但前缘涡未发生破裂,这与文献[15]的结果相似。
由以上分析可以看出,翼身的存在导致背风侧激波位置前移,诱导前缘涡的破裂,使得涡破裂迎角和涡升力均大幅减小。
3 结束语本文采用数值模拟方法研究了跨声速时小展弦比飞翼布局流动特性随迎角的演化规律,分析了翼身厚度对飞翼布局涡升力特性和流动特性的影响。结果表明:在无前缘涡区和前缘涡发展区,薄厚飞翼模型涡升力系数基本相同,但翼身厚度将导致涡破裂迎角和涡升力系数大幅减小。在无前缘涡区,翼身的存在在机头处产生侧洗作用,在尾部由于翼身厚度较大,收缩较快,出现激波诱导边界层分离流动。在前缘涡发展区,翼身厚度引起的侧洗作用使飞翼模型前缘涡形成较晚,影响区域减小,但强度增大,在背风侧诱导的吸力增加,使得前缘涡升力基本不变。翼身厚度导致了背风侧激波位置前移,诱导了前缘涡的破裂,使得涡破裂迎角大幅减小,破裂点前移幅度增大。
| [1] | Roman D, Allen J B, Liebeck R H. Aerodynamic design challenges of the blended-wing-body subsonic transport[R]. AIAA Paper 2000-4335, 2000. |
| [2] |
阎超, 李亭鹤, 黄贤禄.
三角翼上分离及涡流的数值模拟[J]. 力学进展 , 2001, 31 (2) : 227–244.
Yan Chao, Li Tinghe, Huang Xianlu. Numerical simulation of separation and vertical flows on delta wings[J]. Advances in Mechanics , 2001, 31 (2) : 227–244. |
| [3] |
王运涛, 张玉伦, 王光学.
三角翼布局气动特性及流动机理研究[J]. 空气动力学学报 , 2013, 31 (5) : 554–558.
Wang Yuntao, Zhang Yulun, Wang Guangxue. Numerical study on flow structure over a delta wing[J]. Acta Aerodynamic Sinica , 2013, 31 (5) : 554–558. |
| [4] |
焦瑾, 杨永, 李喜乐.
基于DES方法的三角翼激波/涡干扰流场数值模拟[J]. 航空计算技术 , 2010, 40 (6) : 72–77.
Jiao Jin, Yang Yong, Li Xile. Numerical simulation of transonic shock-vortex interaction flow on delta wing using DES[J]. Aeronautical Computing Technique , 2010, 40 (6) : 72–77. |
| [5] | Schiavetta L A, Boelans O J. Shock effect on delta-wing vortex breakdown[J]. Journal of Aircraft , 2013, 46 (3) : 903–914. |
| [6] | Erickson G E, Rogers L W. Experimental study of the vortex flow behavior on a generic fighter wing at subsonic and transonic speeds[R]. AIAA Paper 87-1262, 1987. |
| [7] | Konrcoth R, Klein C. PSP and PIV investigations on the VFE-2 configuration in sub- and transonic flow[J]. Aerospace Science and Technology , 2013, 24 (1) : 22–31. DOI:10.1016/j.ast.2012.09.003 |
| [8] | Hummel D. The international vortex flow experiment 2 (VFE-2): Objectives and overview[R]. RTO-TR-AVT-113-P-17, 2009. |
| [9] | Fritz W. Numerical simulation of the peculiar subsonic flow field about the VFE-2 delta-wing with rounded leading edge[R]. AIAA Paper 2008-0393, 2008. |
| [10] | Luckring J M, Dietrich H. What was learned from the new VFE-2 experiments[J]. Aerospace Science and Technology , 2013, 24 (1) : 77–88. DOI:10.1016/j.ast.2011.07.012 |
| [11] | Konrath R, Schroder A, Kompenhans J. Analysis of PIV results obtained for the VFE-2 65 degree delta wing configuration at sub- and transonic speeds[R]. AIAA Paper 2006-3003, 2006. |
| [12] |
李喜乐, 杨永, 张强.
绕跨声速三角翼的激波/涡干扰流场数值模拟[J]. 航空学报 , 2013, 34 (4) : 750–761.
Li Xile, Yang Yong, Zhang Qiang. Numerical simulation of shock/vortex interaction in transonic flow around a delta wing[J]. Acta Aeronautica et Astronautica Sinica , 2013, 34 (4) : 750–761. |
| [13] |
苏继川, 黄勇, 钟世东, 等.
小展弦比飞翼跨声速典型流动特性研究[J]. 空气动力学学报 , 2015, 33 (3) : 307–312.
Su Jichuan, Huang Yong, Zhong Shidong, et al. Research flow characteristic of low-aspect-ratio flying-wing configuration at transonic speed[J]. Acta Aerodynamic Sinica , 2015, 33 (3) : 307–312. |
| [14] |
李永红, 黄勇, 王义庆, 等.
翼身相对厚度对小展弦比飞翼布局跨声速气动特性及流动机理的影响研究[J]. 空气动力学学报 , 2015, 33 (3) : 302–306.
Li Yonghong, Huang Yong, Wang Yiqing, et al. Wing body thickness effect on aerodynamic characteristic of common low- aspect-ratio flying-wing configuration transonic flow[J]. Acta Aerodynamic Sinica , 2015, 33 (3) : 302–306. |
| [15] | Jobe C E. Vortex breakdown location over 65 deg delta wings empiricism and experiment[J]. The Aeronautical Journal , 2004, 108 (7) : 475–478. |
 2016, Vol. 48
2016, Vol. 48


