推力转向控制是一种新型的控制技术,它是通过偏转发动机出口的喷流方向,利用喷流反作用力在垂直发动机轴线的分量产生的力矩对飞行器进行控制,可以用来补充或代替常规气动操纵面。与常规舵面相比,推力转向控制具有响应时间快、控制力矩大和能在极低速或真空中使用等优点[1-3],可以大大提高飞行器的机动能力和过失速飞行的控制能力,已经在国外先进的第四代战斗机,如美国的F-22,和许多第三代半战斗机上得到验证或应用[4-6]。目前常用的推力转向技术是通过偏转喷管或在喷管内外加挡板来实现,这种机械式偏转方式通常需要复杂的机械机构,维护复杂、成本昂贵,并且需要付出巨大的重量代价。而流体二次引射推力转向技术是一种新型的推力转向控制技术,它通过向发动机喷管主流中引入二次流,并利用二次流与主流的干扰改变推力方向,实现推力转向。与机械式推力转向技术相比,流体二次引射推力转向技术具有机械结构简单、重量轻、响应时间快、隐身特性好、不存在机械和密封故障等优点,使得这种矢量偏转控制技术具有较高的性价比,受到国内外学者的广泛关注。
在流体二次引射推力转向技术研究方面,美国NASA和相关工业部门从20世纪90年代开始进行了相关的研究工作[4-7],启动了多项合作研究计划,系统研究了流体推力转向的作用机理,对比分析了不同推力转向控制方案的效率,建立了多种流体推力转向控制试验和计算方法,探索了流体推力转向控制的排气喷管概念设计方法,取得了大量的研究成果。国内推力转向控制技术研究起步相对较晚,前期工作主要集中在机械式推力转向控制方面,并得到了初步的应用。而在二次流体引射这种新型流体推力转向控制方面,国内仅部分大学和研究机构开展了相关的研究工作[8-9],距离实际应用还有一段距离。
本文通过数值模拟手段,对流体二次引射推力转向技术进行了数值模拟研究。首先采用二元矩形矢量喷管,结合试验数据,验证了自主开发的流体推力转向数值模拟软件的可靠性;在此基础上,开展了流体二次引射推力转向的机理和各种参数影响规律数值模拟研究,详细研究了不同主次流压比、引射缝隙位置、缝隙宽度等参数对干扰流场结构及推力转向偏角的影响,获得了各设计变量对喷管性能及内部流态的影响规律,给出了流体二次引射实现推力转向的基本设计原则及较优的参数组合方案,为未来中国战斗机或现有战斗机应用流体推力转向提供技术支持和技术基础。
1 流体二次引射推力转向基本原理流体二次引射推力转向技术从基本原理上大体可分为3类(图 1)[7]:第1类是在发动机喷管喉道附近引入引射气流,借助引射气流与主流的干扰改变喉道附近声速线形状,使得发动机喷管的有效喉部产生不对称移动,达到改变推力方向的目的,图 1(a)为第1类偏转机理的示意图;第2类是在喷管出口附近垂直喷管壁面引入二次气流,利用引射气流对主流的阻挡效应形成的激波来偏转喷管主流的方向,从而达到推力转向的目的,图 1(b)为第2类偏转机理的示意图;第3类与前两类不同,不是向主流垂直引射二次流,而是在喷管出口平行引入二次流,引射气流相当一块档板置于喷流一侧,在主喷管和套管之间狭槽采用吹吸气,使主流与次流形成相反的逆向流动,使得主流在流向喷管出口时向吸气方向偏转,从而产生推力矢量偏转,图 1(c)为第三类偏转机理的示意图。

|
图 1 3类流体推力转向机理示意图 Figure 1 Sketch map of mechanism for three types of fluidic thrust vectoring |
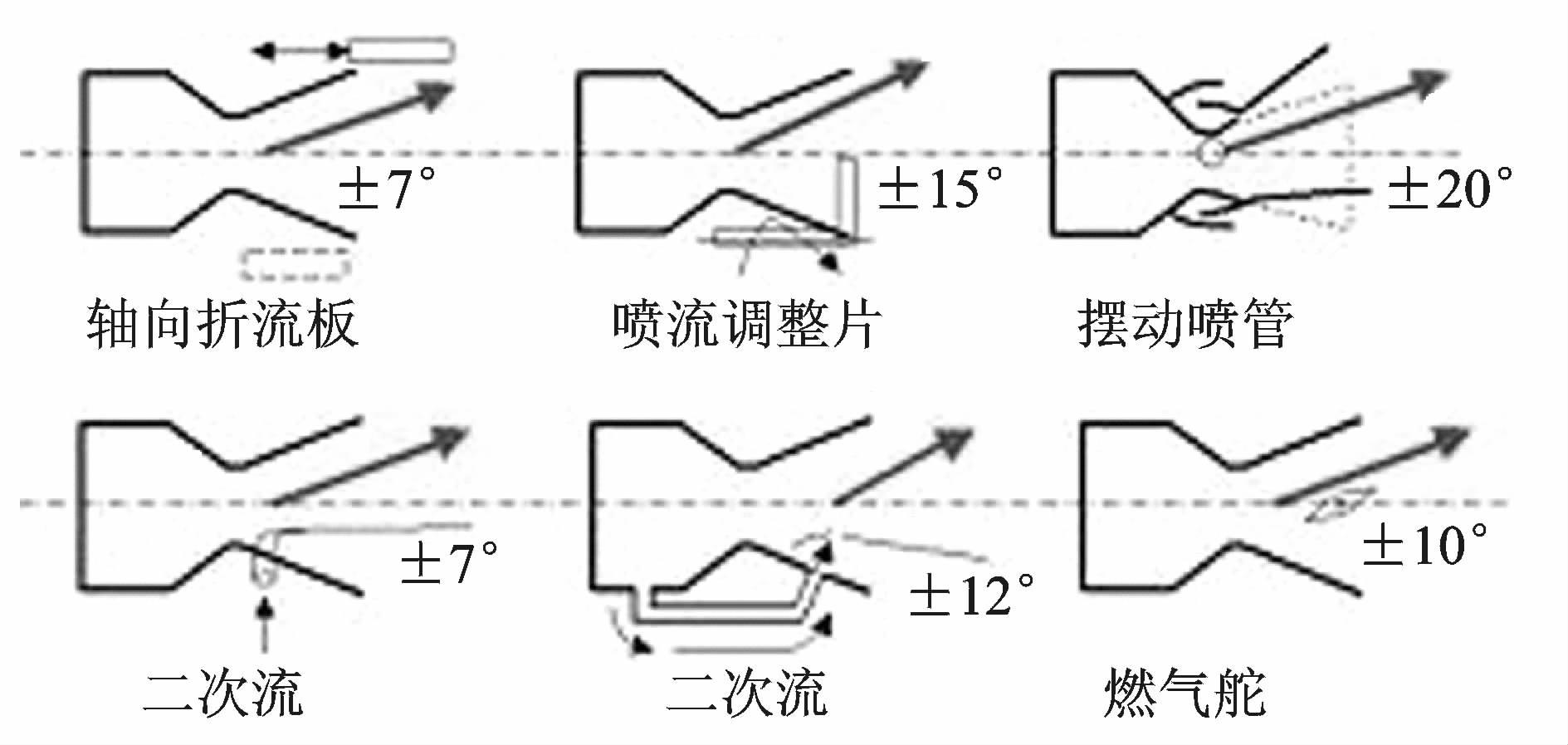
围绕上述3种类型的流体推力矢量概念的大量研究[10]表明:第1类喉部移动方法可以产生最有效的推力转向,流体控制的总压损失最小,但是控制比较困难;第2类矢量激波控制方法可以获得较大的推力矢量角,但是能量损失较大;而第3类的逆流方法综合效果可能最好,但是会发生逆流附着到套管表面和偏转延迟的情况。图 2是几种不同推力矢量控制方法的偏转能力比较示意图。
|
图 2 不同推力矢量控制方法的转向能力示意图 Figure 2 Ability of thrust vectoring by different methods |
2 数值模拟软件介绍及验证 2.1 数值模拟软件介绍
本文采用中国空气动力研究与发展中心自主研制的亚跨超声速流场解算器MFlow进行计算。MFlow解算器是基于格心的非结构混合网格和雷诺平均NS方程的大规模并行流场解算器,广泛应用于航空航天领域飞行器气动特性评估。经过大量标准算例的考核[11-12],它可以使用任意形状的网格单元,具有较大的灵活性。该计算器采用有限体积法对空间进行离散,未知变量位于网格单元的体心。离散方程组的求解采用隐式LU-SGS方法或显式Runge-Kutta方法,采用FAS融合多重网格方法加速收敛。MFlow解算器有各种不同的选项可以使用,例如各种空间对流项和粘性项离散格式、各种时间迭代方法、不同的湍流模型等。
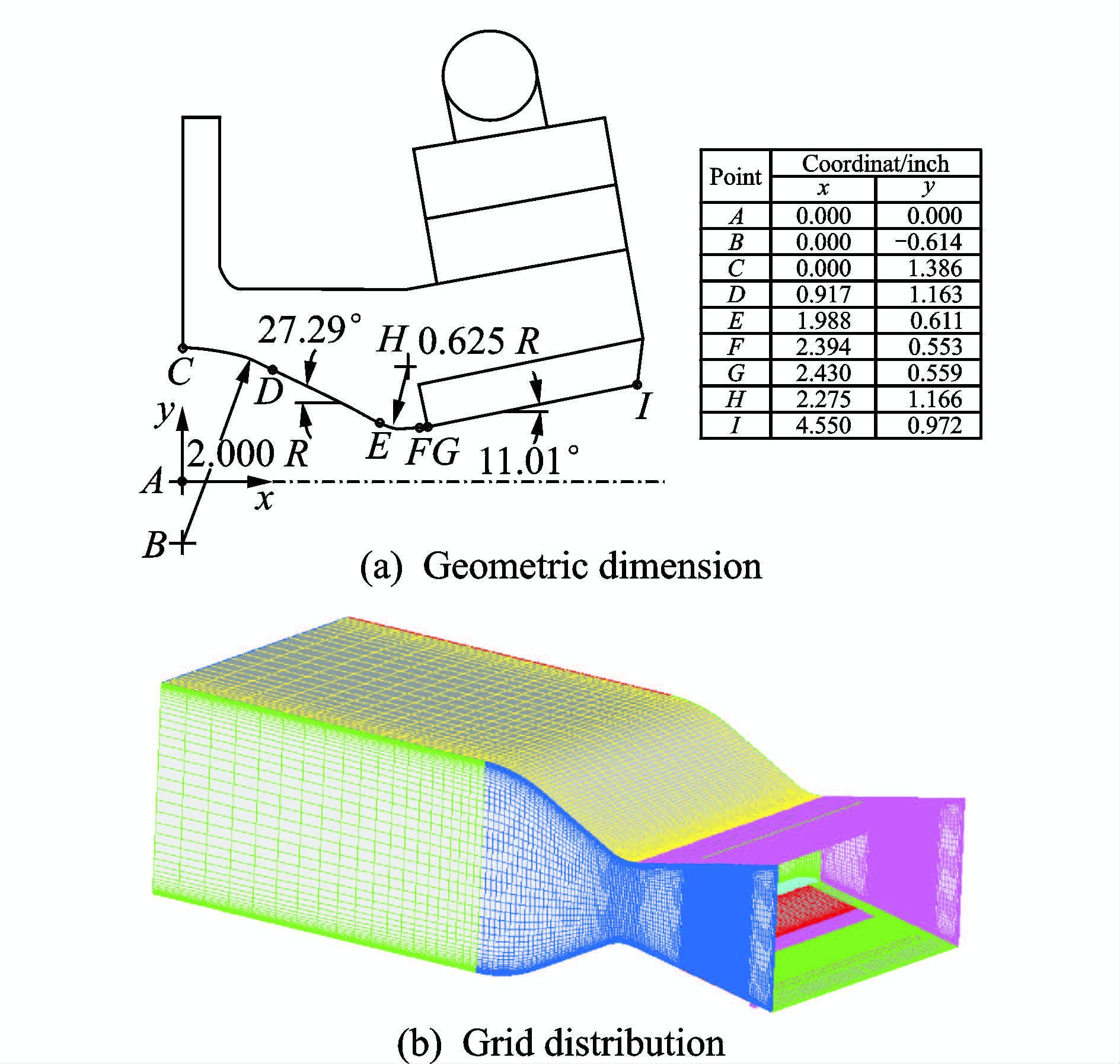
2.2 数值方法验证为了验证MFlow软件对流体二次引射推力转向的数值模拟能力,对一二元矩形矢量喷管进行了数值模拟验证,喷管的设计压比为8.78,设计出口马赫数为2.075,详细参数见文献[13]。主流的压比变化范围为4.6~10,次流的压比变化范围为0.4~1.0,喷管的外形尺寸及表面网格分布如图 3所示。喷管内外部计算网格总量约为150万个,在喉道附近和缝隙前后分离区域都进行了加密处理,喷管内部物面网格y+值约等于1,每一个计算模型的附面层内大约有50个网格点,喷管出口的下游网格距离喉道50倍喉道高度,外流边界为20倍喉道高度。
|
图 3 二元矩形喷管尺寸及表面网格分布 Figure 3 Geometric dimension and grid distribution for rectangular nozzle |
本文数值模拟控制方程采用三维可压缩N-S方程,考虑到所研究的流场包含激波、分离、激波与边界层相互干扰、激波和旋涡结构相互干扰等复杂流场结构,采用了耗散较小分辨率较高的Roe差分格式。文献[14, 15]中指出,SA一方程湍流模型在偏离喷管设计工况下不能很好地模拟喷管内流激波的位置,因此本文数值模拟选择二方程SST湍流模型。主流和二次流的边界条件采用驻室边界条件,即给定驻室的总温和总压。
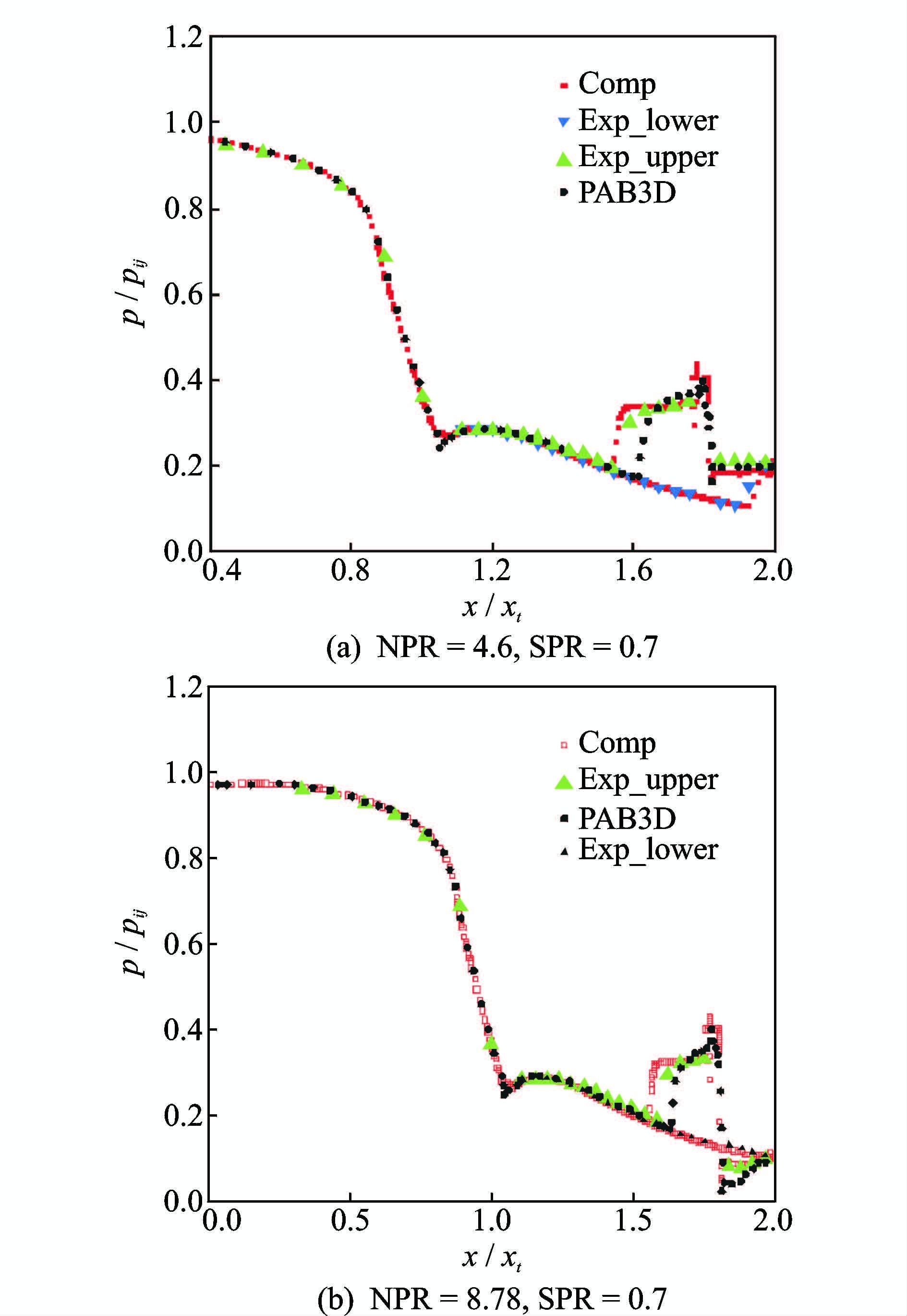
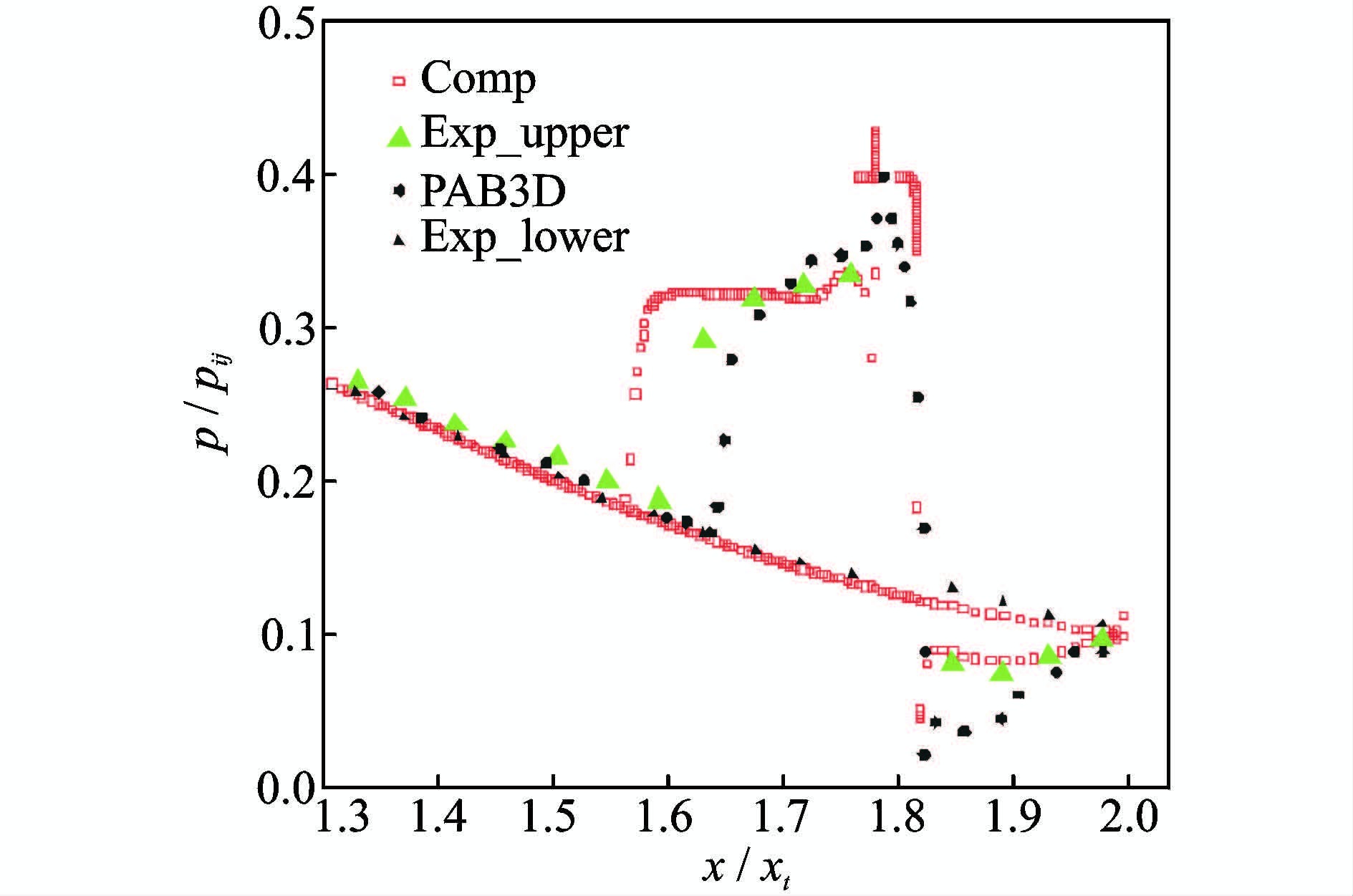
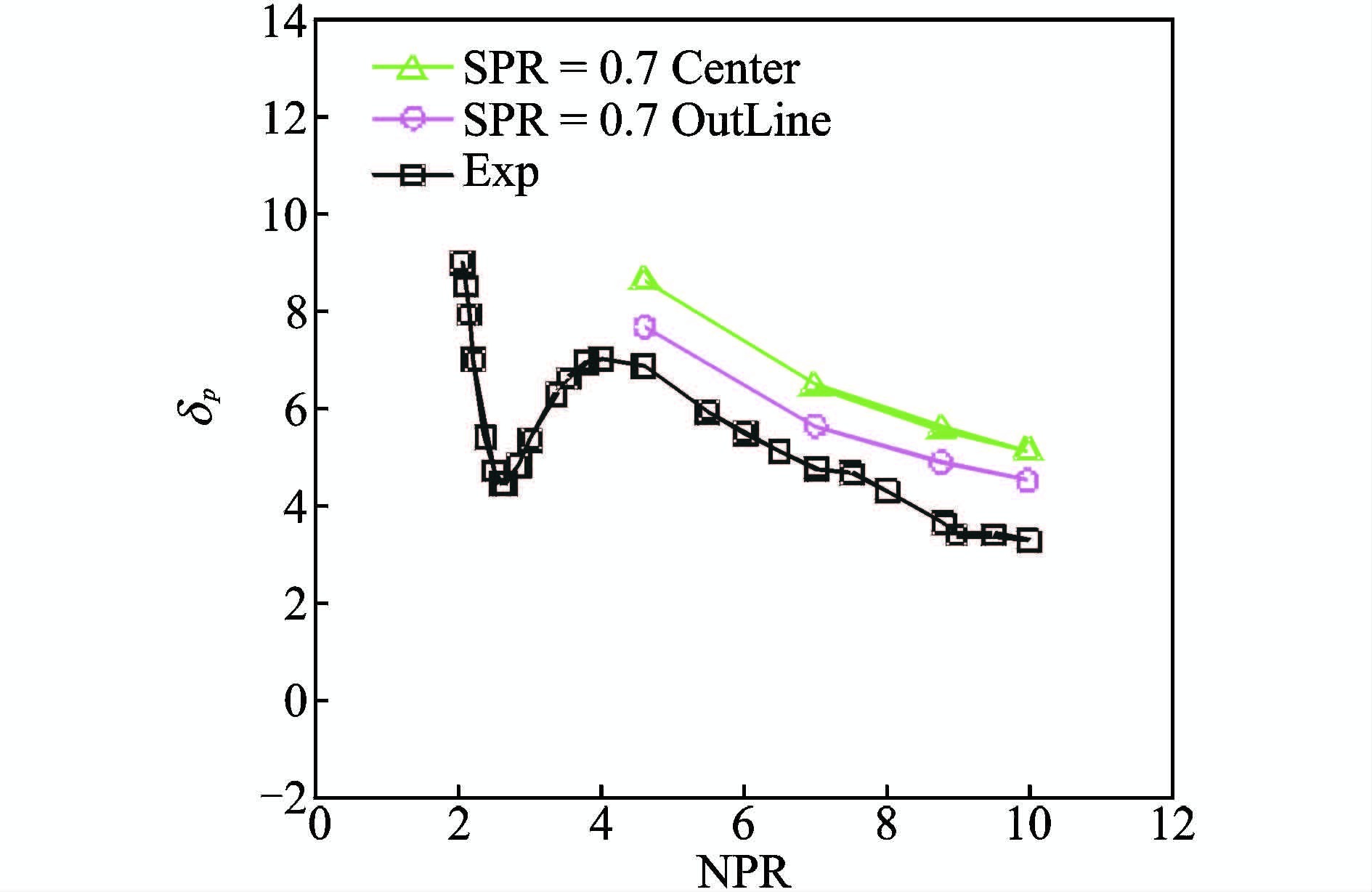
图 4,5给出了不同主流和次流压比时喷管表面压力分布对比曲线,图中NPR表示主流总压比,SPR表示次流总压比。对比曲线可以看出,在斜激波上游未受到扰动的流场区域,计算结果、试验数据[13]和国外计算结果[13]压力分布相一致;在受到扰动的区域,计算结果和试验数据在激波位置上有一定的差别,主流总压比8.78,次流压比0.7时试验结果的分离位置大约在x/xt=1.6处,而数值计算的分离位置要靠近喉部,大约在x/xt=1.56处附近,在数值模拟的几个工况下,都有这种趋势,这可能和湍流模型有关。图 6 给出了推力转向角度δp随主流总压比NPR变化曲线对比,其中图标号为三角的为喷管中心处的偏转角,图中标号为圆圈的是喷管出口的平均偏转角,比较可知喷管中心处的偏转角最大,因为受到喷管侧壁的影响,喷管出口的平均偏转角要小于中心处偏转角,数值计算的偏转角要大于试验结果,但是考虑到试验结果取的是误差带中间结果,数值计算的偏转角与试验偏转角吻合较好。总的来说,计算与试验值吻合较好,计算软件能够准确地描述二次流引射流场的细节,验证了计算软件的可靠性。
|
图 4 不同控制工况下压力分布对比 Figure 4 Comparison of pressure distribution in experiment and reference at different conditions |
|
图 5 局部压力分布对比 Figure 5 Pressure distribution comparison at typical position |
|
图 6 推力转向角对比曲线 Figure 6 Comparison of thrust vector angle with experimental data |
3 计算结果分析 3.1 计算模型
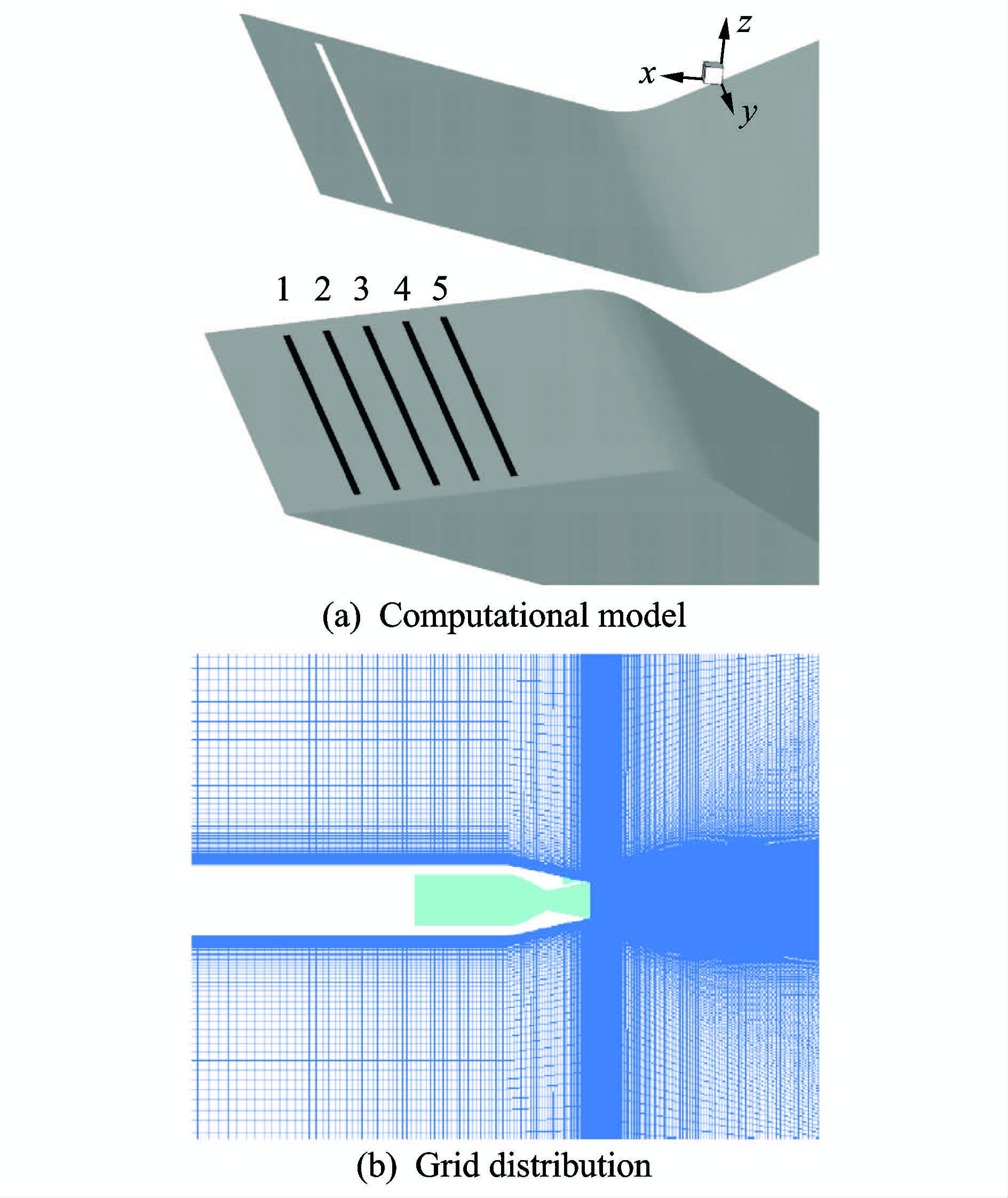
计算模型采用验证算例中的二元矩形矢量喷管,在喷管扩张段上表面5个不同位置开了两种不同宽度的缝隙,位置1距离喷管出口10.922 mm,位置5最靠近喉道处,不同缝隙的间距为5.842 mm,两种不同缝隙宽度分别为1.016和2.032 mm,具体外形及网格分布如图 7所示。
|
图 7 计算模型及网格分布示意图 Figure 7 Computational model and grid distribution |
3.2 流动结构分析
在收敛扩张型喷管的扩张段引入二次流后,喷管内部主流流动会在引射缝隙附近被二次流阻挡,在缝隙的上游形成一道较强的斜激波,激波后的压力升高,形成逆压梯度区域,导致喷流上游一定距离处气流沿喷管壁面向上游流动,该逆向气流与喷管壁面附面层及喷流相互作用后形成三维分离流动区,喷管主流与分离区气流相互干扰产生分离激波,分离激波使得喷管主流发生偏转,产生矢量推力。
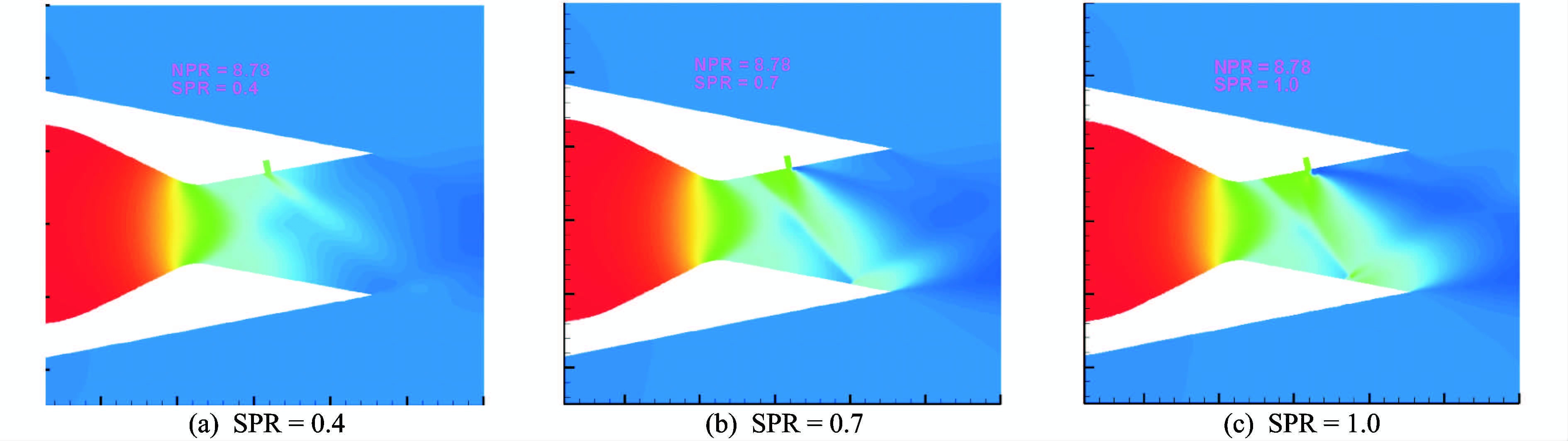
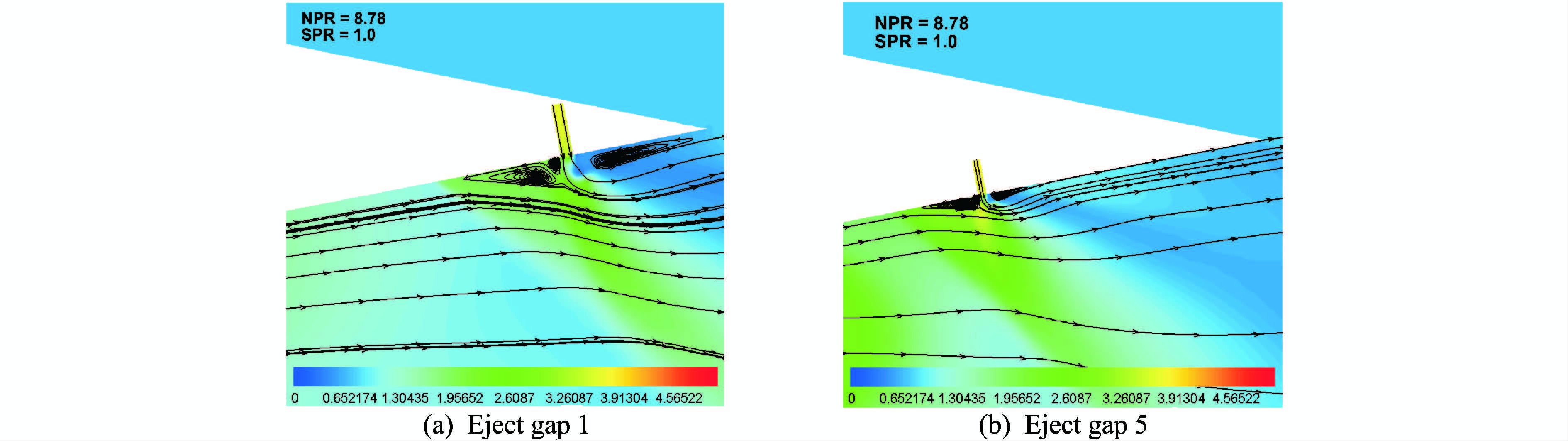
图 8给出了缝隙位于位置5时不同二次流总压比对喷管截面压力云图分布影响,可以看出,增加次流总压比SPR,会引起上游斜激波变强,斜激波的位置向靠近喉道的位置移动,二次流引射引起的表面分离区域扩大。图 9给出了不同缝隙位置二次流附近涡系分布,可以看出,缝隙上游的分离区内有一对旋转相反的涡结构,前一个旋涡成为主分离涡,主分离涡与二次流之间的相互作用,在喷口前形成一个尺度较小的喷流马蹄涡,不同引射缝隙位置对分离涡的大小存在一定影响。
|
图 8 位置5不同二次流压比对喷管截面压力云图分布影响 Figure 8 Pressure contour distributions at different SPRs for eject gap 5 |
|
图 9 不同缝隙位置二次流附近涡系分布及截面压力分布 Figure 9 Distribution of vortex and pressure near the second flow for different eject gap positions |
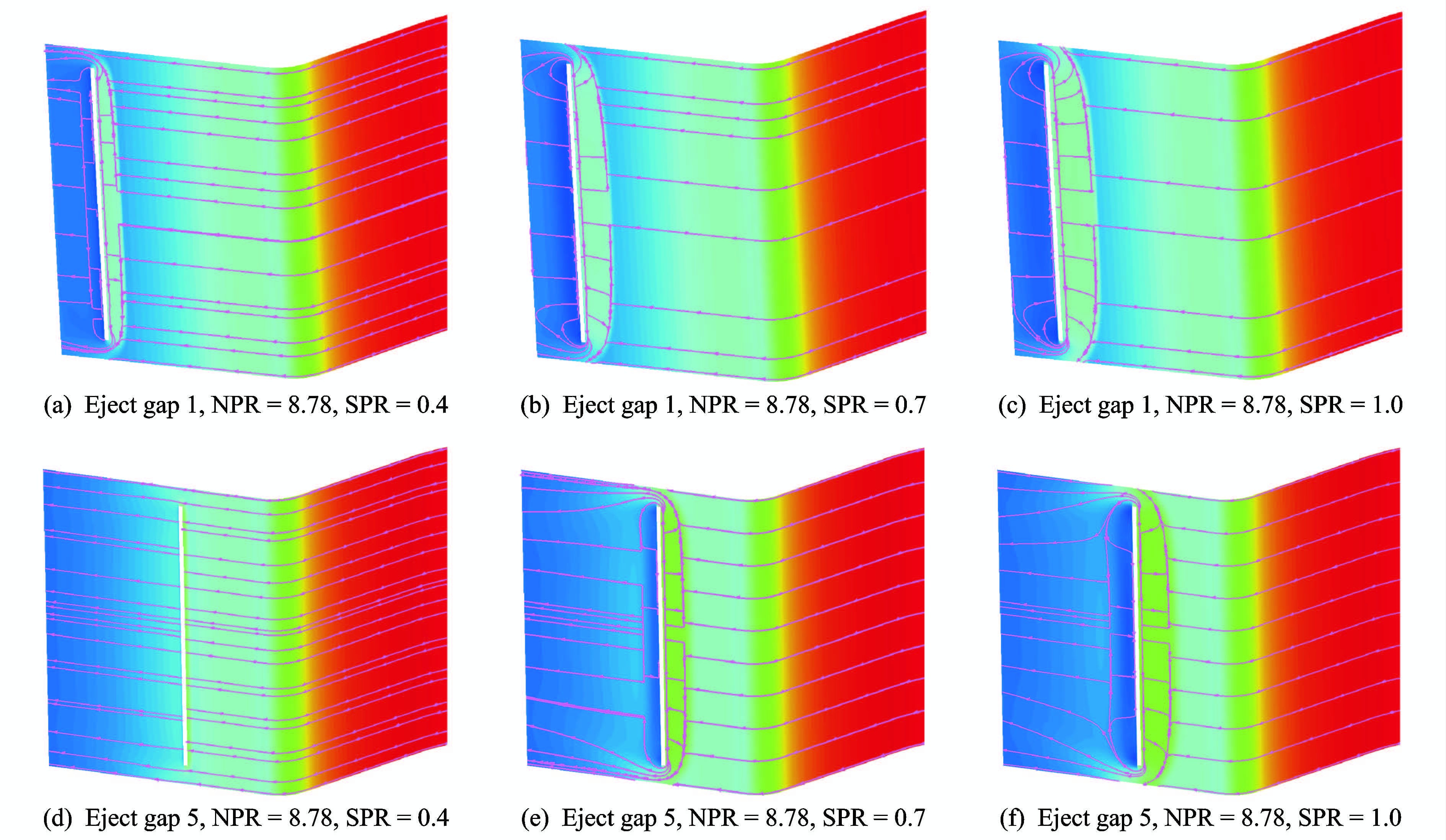
图 10是缝隙位置1(a~c)和缝隙位置5(d~f)在3种不同次流压比情况下的物面极限流线对比图,图中上游主分离涡前缘的极限流线为分离线,喷流马蹄涡前缘的极限流线为主分离涡和喷流马蹄涡的再附线。可以看出,除缝隙位置5,次流压比SPR=0.4以外,不同工况下的流场结构基本相似,随着次流压比的逐渐增大,分离线位置向喉道移动。在相同次流压比时,缝隙位置越靠近喷管出口,分离区域越大。对于位置5 次流压比SPR=0.4时,在缝隙处没有对主流形成足够的阻挡效果,缝隙排出的二次流随着主流马上偏转流向下游,在喷管内部没有形成二次流干扰需要的斜激波结构,所以没有形成理想的偏转所需要的流动结构。
|
图 10 不同次流压比对喷管内表面压力分布及物面流线影响 Figure 10 Comparison of pressure contours and surface streamline distribution at different SPR and for different eject gap positions |
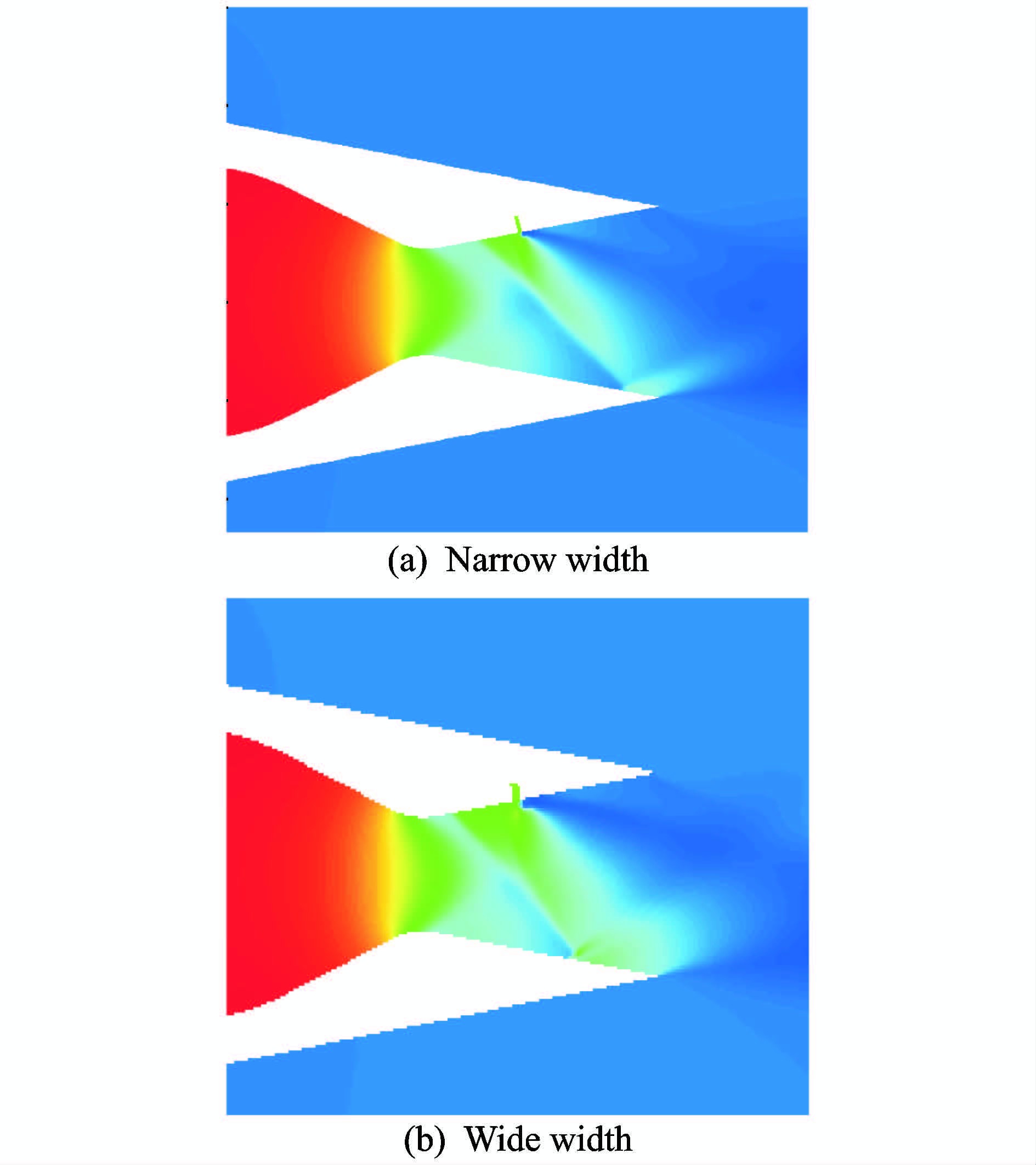
图 11是缝隙位置5不同宽度缝隙时喷管对称面压力分布云图对比,可以看出,缝隙的宽度变化不会改变二次流流场的基本结构,其影响规律与次流总压比SPR的影响趋势相类似,增加缝隙的宽度与增加SPR的效果类似,都可以归结为流量引起的变化。在一定的条件下,二次流引射产生的斜激波会打到喷管的下表面,斜激波会在下表面进行再一次反射,随着流量增加,斜激波打到下表面的位置逐渐向喷管上游靠近。
|
图 11 位置5不同宽度缝隙对喷管截面压力分布影响 Figure 11 Comparison of pressure contours with different width of eject gap 5 |
3.3 参数影响分析
图 12给出了不同位置、不同压比对推力转向偏角影响曲线,比较可知,转向偏角与主流压比NPR、次流压比SPR和缝隙的位置大小都密切相关,在位置3以前,增加二次流的次流压比SPR可以提高推力转向角的偏转角度,最大转向偏角一般都在二次流SPR为1.0时取得,而在位置3以后,最大转向偏角会在SPR为0.7处取得。在各种工况下,最大偏转角都出现在主流压比NPR为2和4.6时,此时喷管处于过膨胀状态。在次流压比SPR为0.4情况下,二次流对主流的阻挡很弱,几乎没有产生偏转所需要的激波结构,所以转向能力较弱,而且缝隙越靠近喉道,推力偏转的能力越弱,大部分偏转角在1°以内。位置5中的次流压比SPR为0.4和SPR为1.0的推力偏转角度曲线在主流压比NPR为6.0附近出现了交叉现象,其原因主要是随着次流压比SPR的增大,喷管上下表面的激波都向喉道方向运动,二次流引起的上表面斜激波打到了喷管下表面内壁,出现了反操纵现象(图 11)。

|
图 12 宽缝隙不同位置,不同SPR对推力转向偏角影响 Figure 12 Thrust vectoring angle change with different eject gap positions and SPRs |
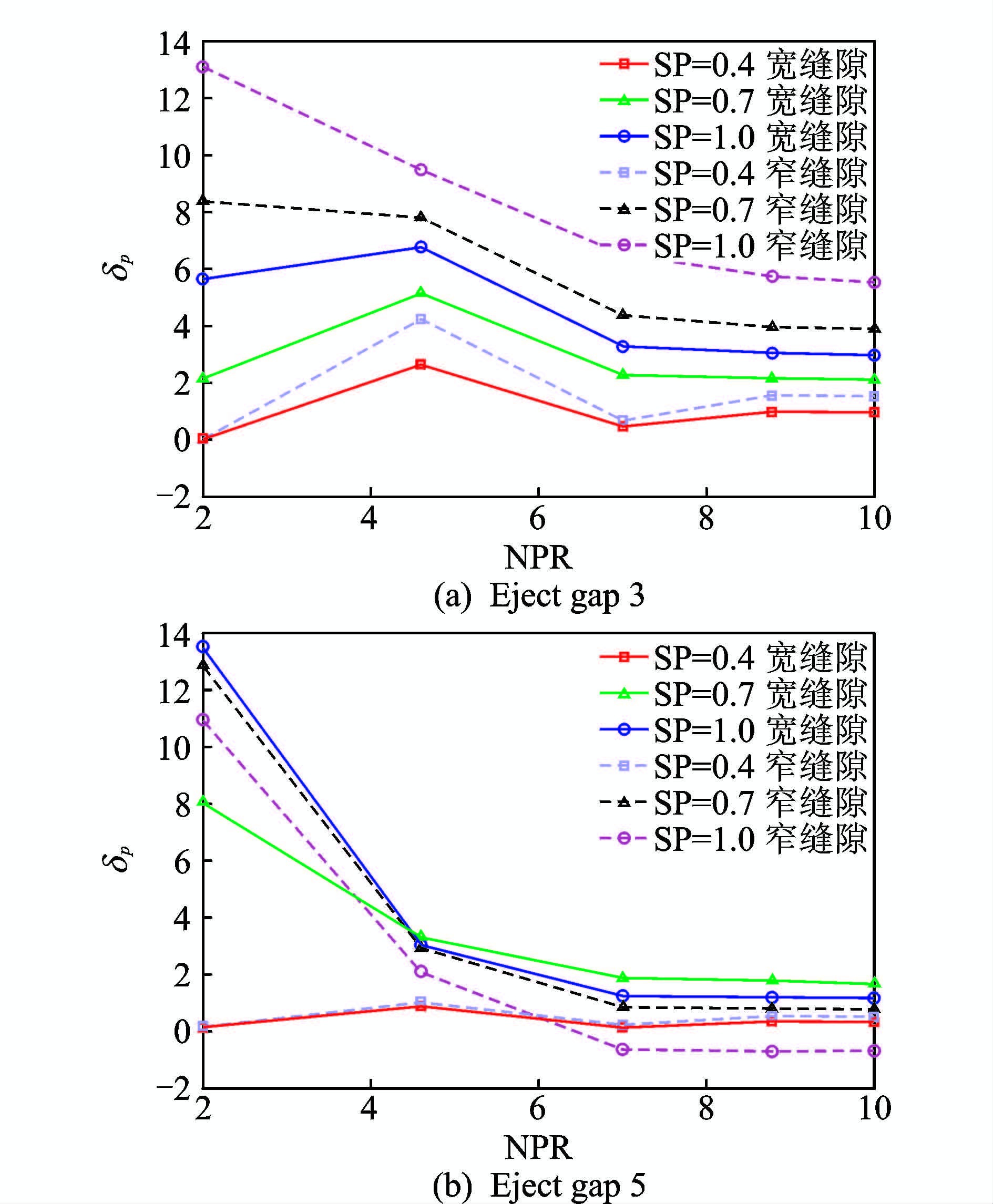
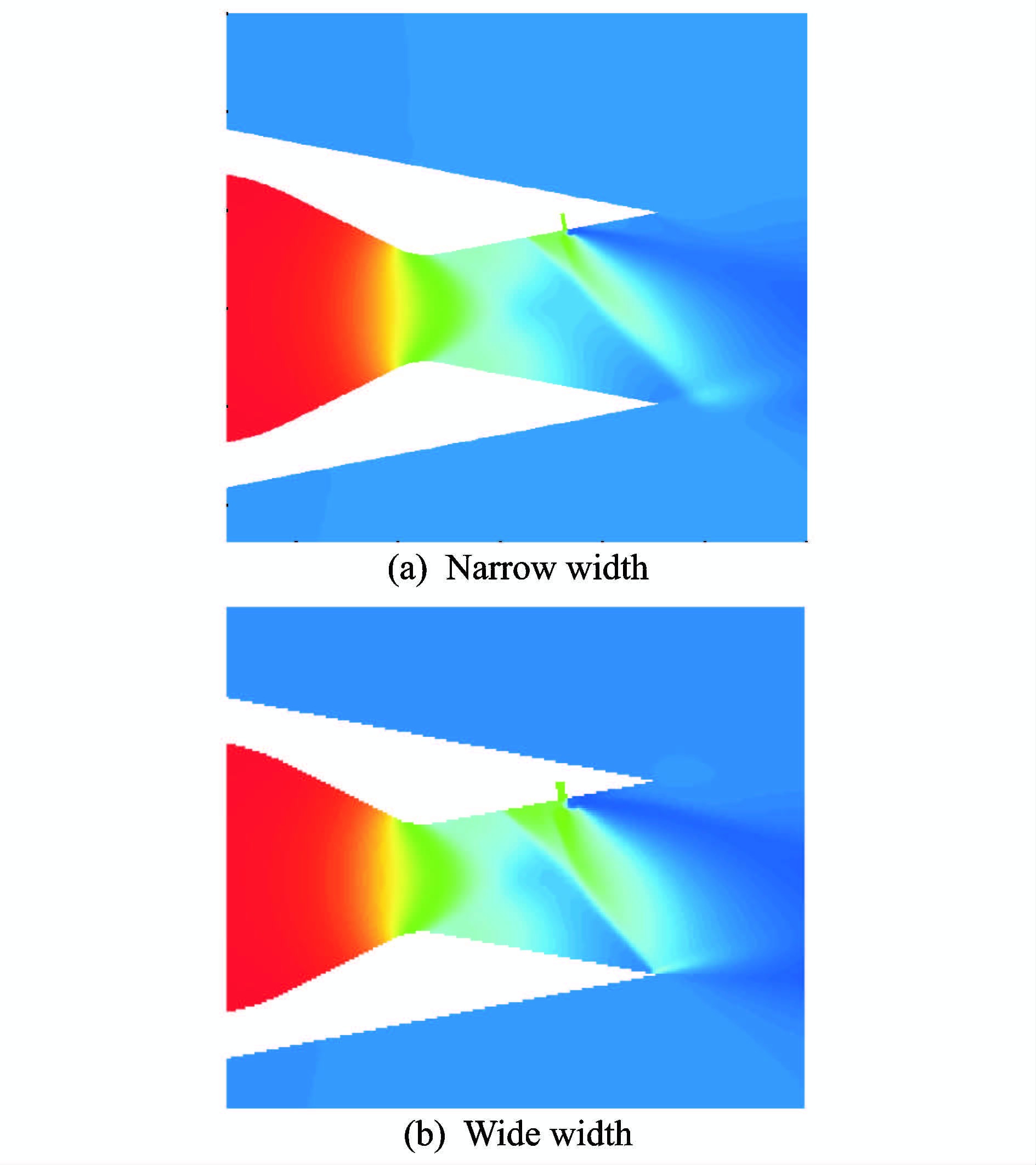
图 13是相同缝隙位置不同缝隙宽度时的喷管推力偏转角度曲线,图中实线表示宽缝隙引射时喷管推力偏转角,虚线表示相同工况下窄缝隙引射时喷管推力偏转角。在位置3处窄缝隙的转向角小于宽缝隙,而在位置5处,窄缝隙的转向角大于宽缝隙的转向角。图 14给出了位置3不同缝隙宽度对流场结构影响,结合图 11可以看出,宽缝隙位置3处的斜激波在下表面出口的边缘,而在缝隙位置5,斜激波打到下表面,并且在下表面反射,气流从喉道出来后,经过二道激波的偏转,使得偏转角减小,所以在二次流产生的斜激波没有打到下表面或者不严重时,宽缝隙的偏转能力要强于窄缝隙。而当斜激波影响到下表面后,下表面对激波的反射减弱了激波的偏转能力,窄缝隙的偏转能力要强于宽缝隙。
|
图 13 相同位置、不同缝隙宽度推力转向效果对比 Figure 13 Comparison of thrust vectoring angle at same position and different width of eject gap |
|
图 14 位置3不同宽度缝隙对喷管截面压力分布云图影响 Figure 14 Comparison of pressure contours with different width of eject gap 3 |
综合以上参数影响规律可以看出,无论是二次引射位置还是引射方式,能否建立偏转需要的流场结构和斜激波是否打到下表面是一个关键因素,斜激波撞击下表面确定了引射的转向性能,要获得较高的偏转效率,应该设计一个二次流引射系统使强斜激波由引射流产生,而不会冲击到对面的表面。
4 结 论本文对流体二次流引射推力矢量喷管的主要设计变量进行了参数化研究,获得了各设计变量对喷管性能及内部流态的影响规律,可以得到以下结论:
(1) 激波偏转矢量的方法可以获得较大的矢量偏转角度,但是为了获得较大的激波偏转角,喷管必须运行在主流压比较小的远离设计状态的过膨胀状态。这样,主流偏转不仅要承受流动穿过激波的能量损失,还要承担喷管运行在过膨胀状态的损失,喷管的推力损失较大。如何在保证较高矢量偏转角的情况下,减小推力的损失是一个苛刻的问题。
(2) 本文建立的推力转向数值模拟软件可以较好地模拟二次流引射的流场细节,计算与试验值吻合较好。
(3) 不同主次流压比、引射缝隙位置及缝隙宽度等参数对干扰流场结构及推力转向偏角会产生较大影响,存在最优的参数组合方案。
(4) 无论是二次引射位置还是引射方式,能否建立偏转需要的流场结构和斜激波是否打到下表面是流体二次引射推力转向设计的关键因素,斜激波撞击下表面确定了引射的转向性能,要获得较高的偏转效率,应该设计一个二次流引射系统使强斜激波由引射流产生,而不会冲击到对面的表面。
| [1] | Hiley P E, Wallace H W, Booz D E. Nonaxisymmetric nozzles installed in advanced fighter[J]. J Aircraft , 1996, 13 (12) : 1000–1006. |
| [2] | Pendergraft O C. Comparison of axisymmetric and nonaxisymmetric nozzles installed on the F-15 configuration[R]. AIAA Paper 1977-0842,1977. |
| [3] | Taylor J G . A static investigation of a simultaneous pitch and yaw thrust vectoting 2-D C-D nozzle[R]. AIAA Paper 1988-2998, 1988. |
| [4] | Giuliano V J,Flugstad T H,Semmes R,et al. Static investigation and computational fluid dynamics (CFD) analysis of flowpath cross-section and trailing-edge shape variations in two multiaxis thrust vectoring nozzle concepts[R]. AIAA 1994-3367,1994. |
| [5] | Federspiel J,Bangert L,Wing D,et al. Fluidic control of nozzle flow-some performance measurements[R]. AIAA Paper 1995-2605, 1995. |
| [6] | Deere K A. Computational investigation of the aerodynamic effects on fluidic thrust vectoring[R]. AIAA Paper 2000-3598,2000. |
| [7] | Chiarelli C, Johnsen R K, Shieh C F. Fluidic scale model multi-plane thrust vector control test results[R] . AIAA Paper 1993-2433, 1993. |
| [8] |
肖中云, 顾蕴松, 江雄, 等.
一种基于引射效应的流体推力矢量新技术[J]. 航空学报 , 2012, 33 (11) : 1967–1974.
Xiao Zhongyun, Gu Yunsong, Jiang Xiong, et al. A new fluidic thrust vectoring technique based on ejecting mixing effects[J]. Acta Aeronautica et Astronautica Sinica , 2012, 33 (11) : 1967–1974. |
| [9] |
李耀华, 李建强, 杨党国, 等.
二元双喉道射流推力矢量喷管流动参数影响的数值研究[J]. 空气动力学报 , 2015, 33 (2) : 211–217.
Li Yaohua, Li Jianqiang, Yang Dangguo, et al. Numerical study of a dual-throat fluidic thrust-vectoring nozzle[J]. Acta Aerodynamica Sinica , 2015, 33 (2) : 211–217. |
| [10] | Karen A. Summary of fluidic thrust vectoring research conducted at NASA Langley Research Center[R]. AIAA Paper 2003-3800,2003. |
| [11] |
张耀冰, 邓有奇, 吴晓军, 等.
DLR-F6翼身组合体数值计算[J]. 空气动力学报 , 2011, 29 (2) : 163–169.
Zhang Yaobing, Deng Youqi, Wu Xiaojun, et al. Drag prediction of DLR-F6 using MFlow unstructured mesh solver[J]. Acta Aerodynamica Sinica , 2011, 29 (2) : 163–169. |
| [12] |
吴晓军, 邓有奇, 周乃春, 等.
尖拱弹身横向喷流数值模拟[J]. 空气动力学报 , 2003, 21 (4) : 464–469.
Wu Xiaojun, Deng Youqi, Zhou Naichun, et al. Numerical simulation of supersonic lateral jet interactions for an axisymmetric body in supersonic flow[J]. Acta Aerodynamica Sinica , 2003, 21 (4) : 464–469. |
| [13] | Kenrick A W, Karen A D, Hampton V A. Experimental and computational investigation of multiple injection ports in a convergent-divergent nozzle for fluidic thrust vectoring[R]. AIAA Paper 2003-3802,2003. |
| [14] | Deere K A. PAB Simulations of a nozzle with fluidic injection for yaw thrust-vector control[R]. AIAA Paper 1998-3254, 1998. |
| [15] | Hunter C A,Deere K A. Computational investigation of fluidic counter/low thrust vectoring[R]. AIAA Paper 1999-2669, 1999. |
 2016, Vol. 48
2016, Vol. 48


