2. 上海冯卡门计算机科技有限公司,上海,201100
2. Shanghai Karmon Terchnology Co.Ltd, Shanghai, 201100, China
在载人航天大力发展、临近空间备受瞩目的今天,稀薄气体动力学的地位日益彰显,而直接模拟蒙特卡洛(Direct simulation Monte Carlo,DSMC)作为解决过渡领域问题[1-2]最有效的方法更是必不可少的。稀薄气体流动的DSMC方法是一种以分子为研究对象的统计方法。这种方法的一般过程可简化为:通过计算机中大量的模拟分子代替真实气体分子[3],这些模拟分子的位置坐标、速度分量等变量会随着分子的运动及碰撞而发生变化。相应地存储模拟分子的位置、速度以及内能后,通过统计网格单元中模拟分子的数量和状态来得到整个流场的计算结果,进而得以模拟真实气体的流动。
在过去的数十年中,为了满足研究需求各异、适应场合不同的飞行器模型的多种要求,发展研究了基于3类不同网格框架的DSMC方法,分别为:结构网格、非结体网格以及直角坐标网格。其中,结构网格[4]有明显的拓扑结构,能够准确地处理边界条件。但其生成过程复杂,尤其是生成复杂几何外形结构网格时,耗费大量的时间和精力;非结构网格[4]的生成适用于任意复杂的几何外形,并且生成速度快。但其单元间关系随机,在处理分子运动、碰撞等位置追踪问题时繁琐、费时。在DSMC方法的发展初期,基于结构、非结构网格的DSMC方法得到了广泛的运用和发展。
直角坐标网格[5-6]生成方法非常简单,生成速度非常快,并且在分子追踪方面也十分高效。但其采用的是正方体网格,网格单元不贴体的致命缺点大大降低了物面的计算精度。本文对传统直角坐标网格进行改进,通过对与物面相交的正方体网格进行切割使单元贴体,并能根据流场的变化对网格区域进行局部加密。这样既保证了直角坐标网格的特点,使DSMC计算过程中搜索效率得到大大提升;同时也保证了物面网格单元的贴体性,提高了物面附近流场的计算精度;还易于实现网格自适应。
1 计算方法在使用数值分析方法进行气体流动分析前,首先要做的工作就是流场网格划分,其质量的好坏直接决定着计算结果的正确性。所以,本文针对改进的直角坐标网格进行介绍。与此同时,也分别对直角坐标网格生成过程中所必不可少的“Bounding Box”方法以及为了提升计算效率而采用的不同于常见的结构、非结构的分子搜索方法进行了阐述。而像稀薄气体动力学基本假设、分子碰撞模型、分子反射模型以及分子能量交换等内容这里就不再赘述。
1.1 计算网格非结构网格贴体的特性大大提高了物面附近计算精度。结合直角坐标网格的特性,本文采用一种新型直角坐标网格处理方法——切割法[7-8],使与物面相交的网格单元贴体。即:采用传统的四叉树方法生成直角坐标网格,再通过切割法对与物面相交的网格单元进行切割使单元贴体。
切割法需要用到计算机图形学的相关裁剪原理,其过程如下:
(1) 找到与物面相交的单元,同时记录该单元被哪些物面线段所切割,进而用这些线段对该单元进行裁剪。
(2) 对裁剪后得到的新线段进行排序,使它们首尾相连。
(3) 通过步骤(1~2)处理得到的有序线段组,构成了每个与物面相交的“切割网格单元”。为了方便计算,每个“切割网格单元”中的线段都按照逆时针方向进行存储,同时记录每条线段的左右单元。
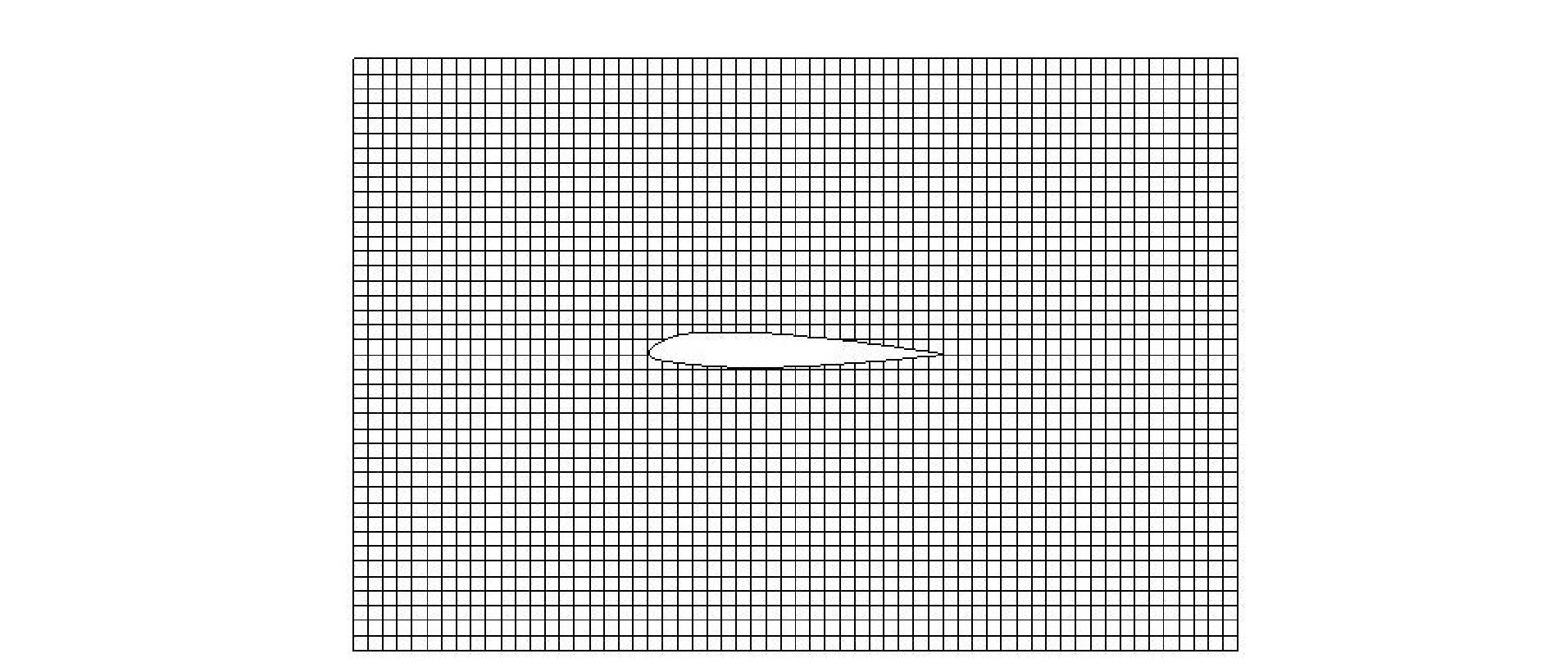
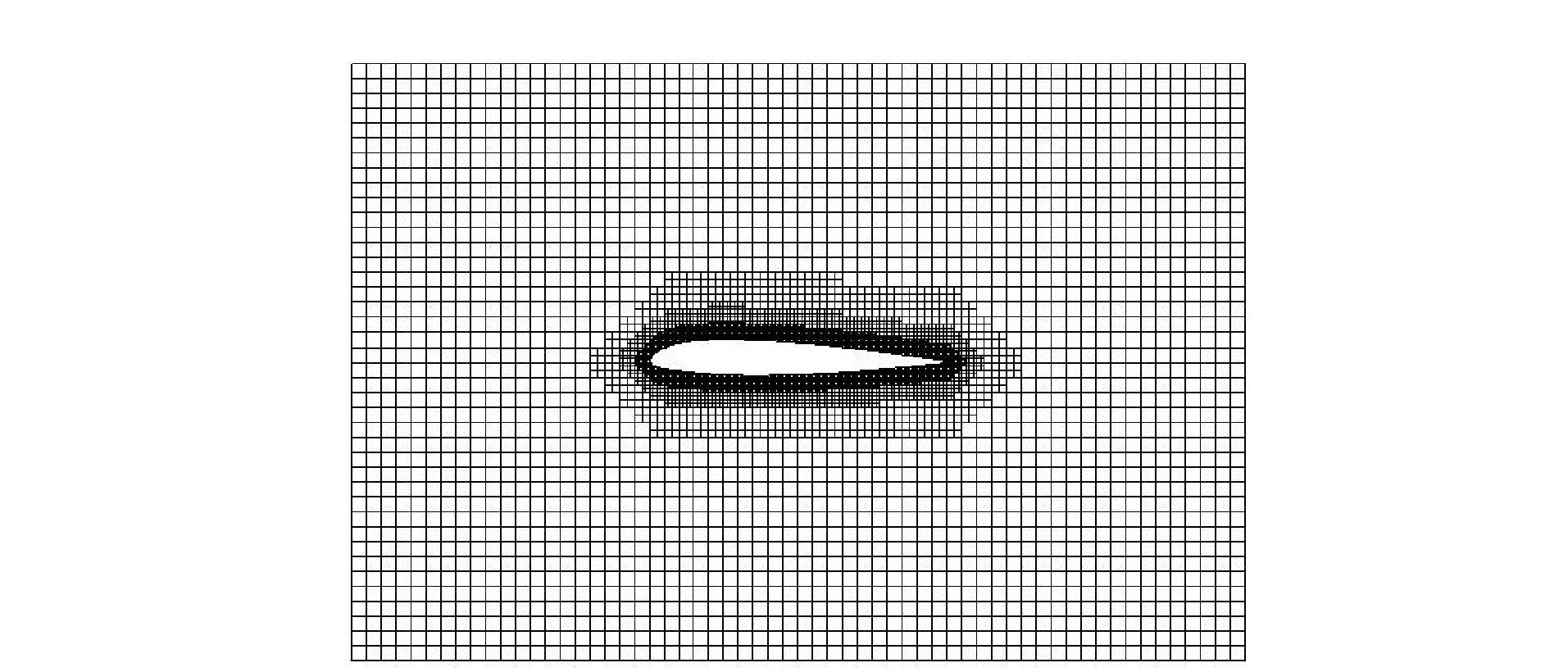
通过上述方法,本文对NACA23012翼型进行网格生成,得到的网格如图 1所示。此外,本文基于“Bounding Box”方法(1.2节中进行介绍)和曲率加密方法,编写了网格加密程序,对NACA23012翼型物面附近进行3次加密,得到网格如图 2所示。
|
图 1 NACA23012切割单元直角坐标网格 Figure 1 Cut-cell Cartesian mesh around NACA23012 |
|
图 2 NACA23012物面加密网格 Figure 2 Surface mesh refinement around NACA23012 |
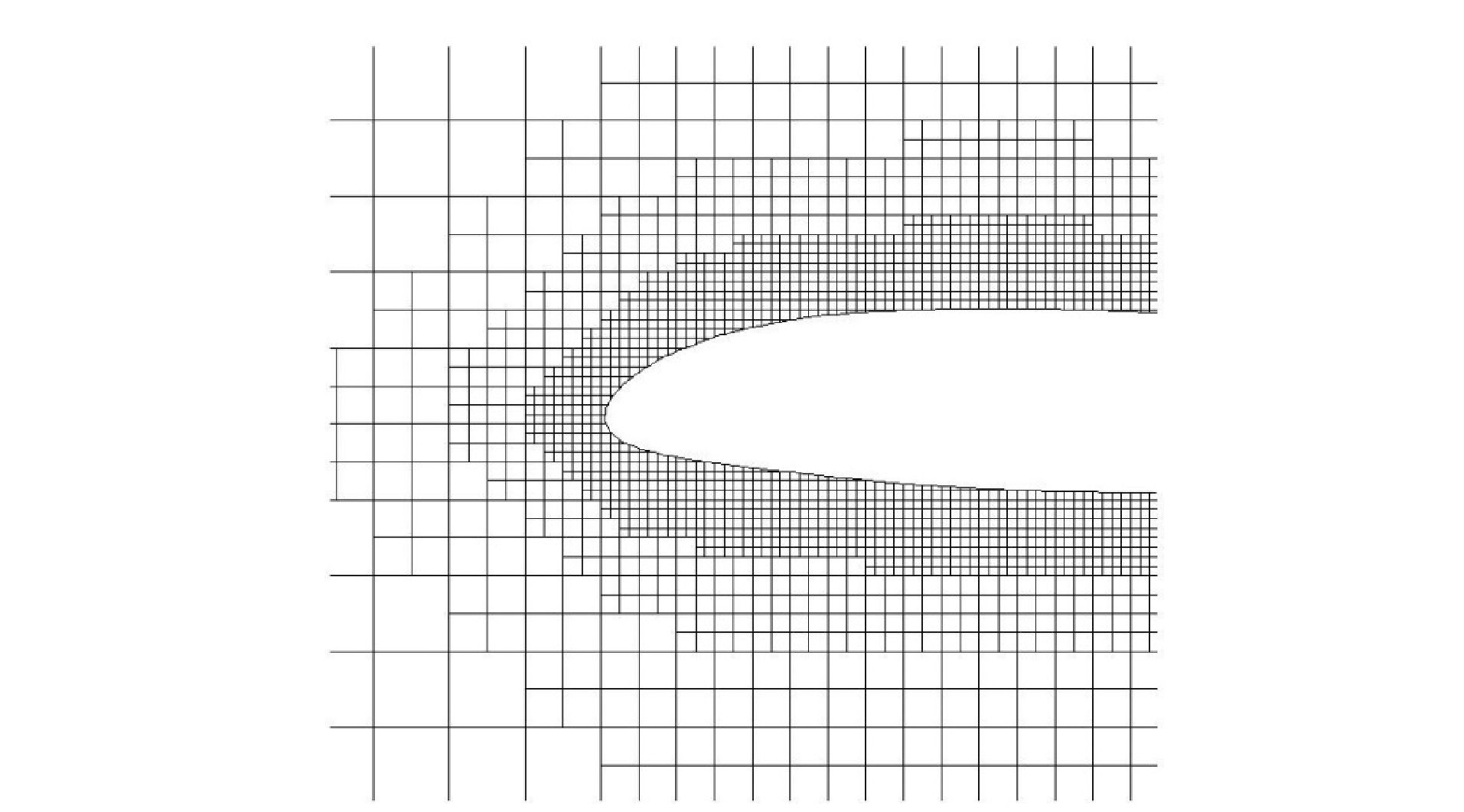
通过本文所采用方法生成的网格,在弥补传统直角坐标网格缺点的同时也保留了直角坐标网格的优势。从图 3翼型前缘附近的网格可以看出,物面相交单元网格的任意性保证了网格的贴体性。
|
图 3 NACA23012前缘网格 Figure 3 Mesh around NACA23012 leading edge |
1.2 Bounding Box方法
在研究直角坐标网格的生成和加密、判断分子是否与物面相撞等过程中,均需要判断网格、分子的运动轨迹等是否与物面相交,这些判断繁琐、耗时,因此如何有效地减少判断次数、提升计算效率显得尤为重要。本文采用“Bounding Box”技术来解决这一问题。
“Bounding Box”技术即“限制盒”方法,其基本思路:为所需判断的物体外形或离散线段选择合适的“限制盒”。先判断网格单元是否与“限制盒”相交,若与“限制盒”相交,再判断是否与物体外形或离散线段相交;若不与“限制盒”相交,则必然不与物体外形或离散线段相交,无需再进行判断。
具体步骤如下:
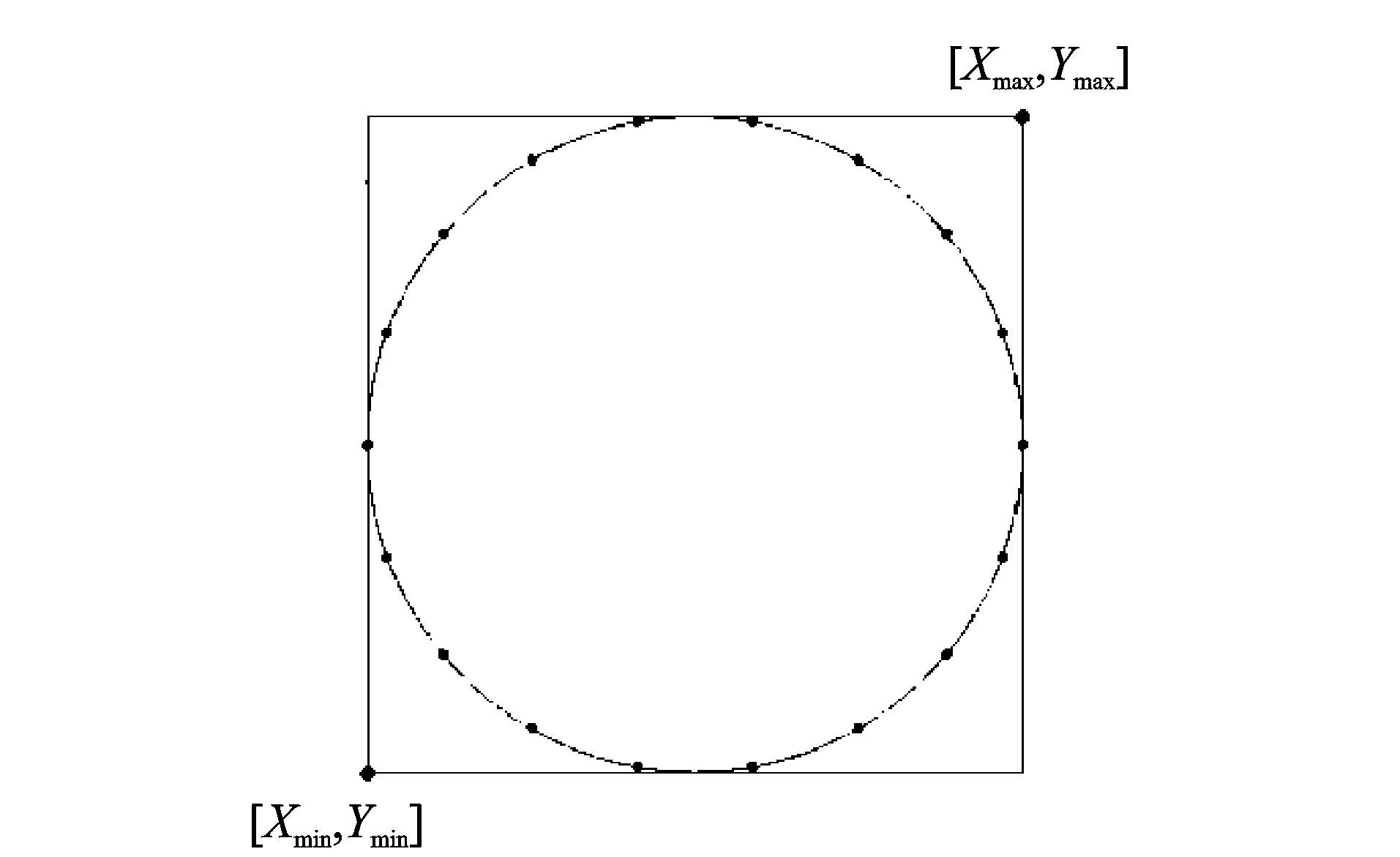
(1) 为需要判断的外形选择合适的“限制盒”,其形状为长方形。“限制盒”的范围通常情况下取X和Y方向上的2个极限值。图 4所示为圆的限制盒,其坐标范围为[Xmin,Xmax],[Ymin,Ymax]。
|
图 4 限制盒 Figure 4 Bounding box |
(2) 判断网格单元或分子运动轨迹与“限制盒”的关系。只需用网格单元或分子运动轨迹的极限坐标与“限制盒”的极限坐标进行简单的比较即可,其判断关系为
| $\left\{ \begin{align} & {{X}_{1,min}}\le {{X}_{2,max}},{{Y}_{1,min}}\le {{Y}_{2,max}} \\ & {{X}_{2,min}}\le {{X}_{1,max}},{{Y}_{2,min}}\le {{Y}_{1,max}}~ \\ \end{align} \right.$ | (1) |
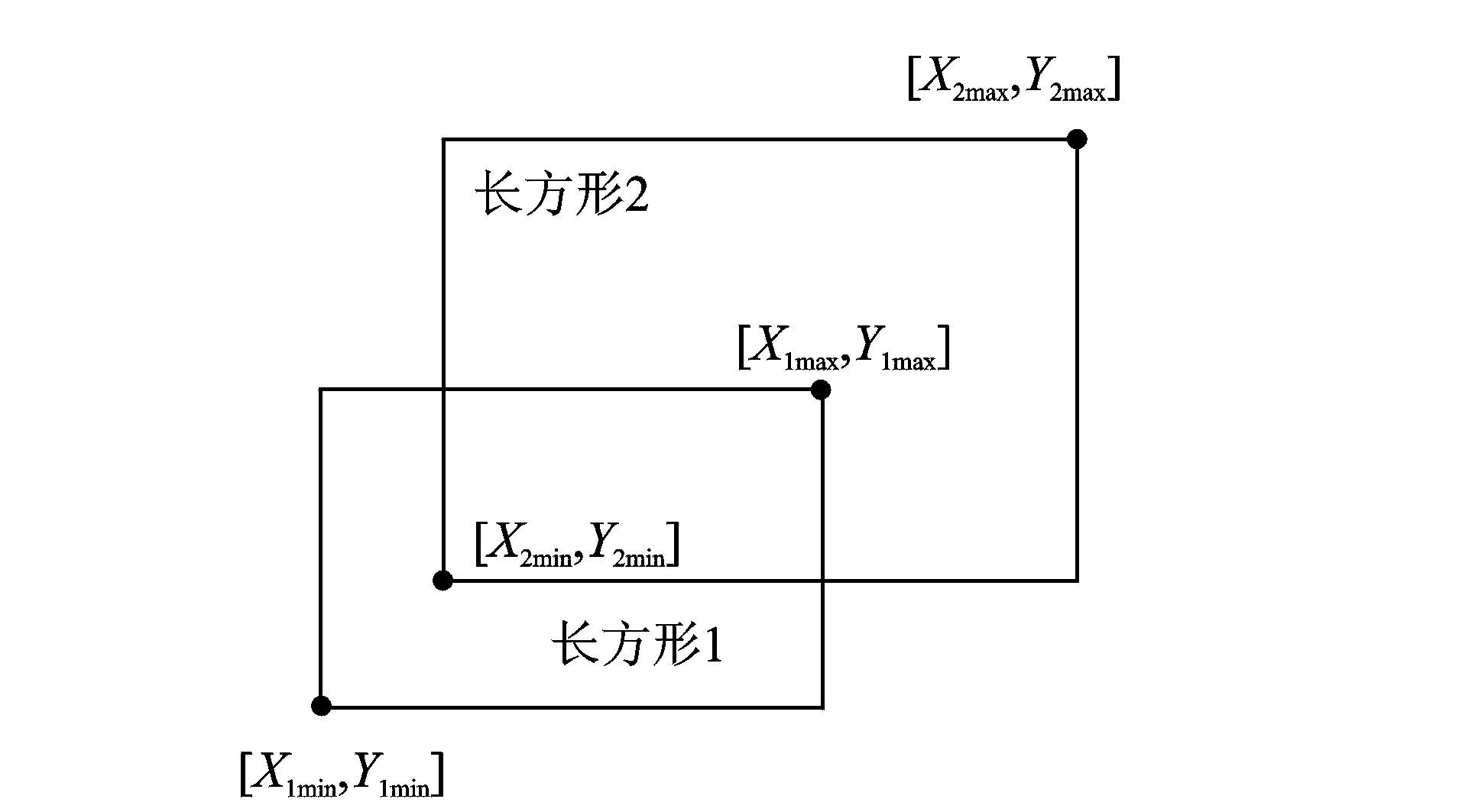
限制盒相交关系如图 5所示,若长方形1与长方形2相交或者长方形2包含长方形1,则必然满足式(1)。若不满足式(1),则能确定网格单元或分子运动轨迹不与物面相交,能快速地将位于“限制盒”外的情况排除掉。
|
图 5 限制盒相交关系 Figure 5 Overlapping relation between bounding boxes |
(3) 在步骤(2)中若判定为与“限制盒”相交,则再将物面分为多条离散线段,并对这些线段选择合适的“限制盒”,重复步骤(1~2)确定可能与哪些具体的线段相交。
通过这种方法能大大提高物面相交判断的速度,与逐一判断是否与物体的所有离散线段相交相比要快很多,大幅减少了计算时间。
1.3 分子搜索方法DSMC方法是通过大量模拟分子代替真实分子从而模拟真实流动的,这些模拟分子的位置坐标、速度分量等变量会随着分子自身运动及分子间相互碰撞而发生变化。所以,在整个DSMC方法计算过程中要耗费大量的计算机资源来记录这些数据。
如何快速地判断出分子所在的单元即分子搜索问题是迫切需要解决的问题。对于非结构网格或结构网格,通常采用相邻单元搜索方法[9]:判断分子运动轨迹与各边关系,若相交则找到对应边相邻单元继续判断,若不相交则表示已经找到分子所处的单元。这种方法缺点在于不仅要循环单元的所有边,还要在每次判断分子运动轨迹与单元边是否相交时进行4次三角形面积的计算,循环次数多且计算量大。
为了提升分子搜索的计算速度,结合传统直角坐标网格的特点,采用位置坐标判断法:将初始流场划分为N1×N2个长方形区域,通过分子坐标判断来确定分子所处的单元
| $\left\{ \begin{align} & {{N}_{x}}=\left( x-{{x}_{min}} \right)/dx+1 \\ & {{N}_{y}}=(y-{{y}_{min}})/dy+1 \\ & {{N}_{cell}}={{N}_{x}}+{{N}_{y}}\times N{{~}_{1}} \\ \end{align} \right.$ | (2) |
式中:xmin,ymin分别为流场边界在x,y方向上的最小值;dx,dy为初始流场每个长方形单元的宽度和高度;Nx,Ny为分子所处列数、行数,在计算过程中只保留小数点之前的整数部分;Ncell为单元所处的单元号。
分子搜索示意图如图 6所示,根据式(2)可以快速地判断出单元所在的位置。

|
图 6 分子搜索示意图 Figure 6 Searching sketch of molecular |
网格进行加密处理后,可以先计算出分子所在父单元编号,再通过类似的方法判断分子所处子单元编号直至找到最后所处位置。
2 优化方法DSMC方法的原理是通过大量模拟分子的运动近似真实分子流动,从而模拟真实流动。为了满足计算精度,在网格单元中投入的模拟分子所代表的真实分子数不能太大,若单个模拟分子所代替的真实分子数太小又将影响程序的计算效率,因此,模拟分子的选取至关重要。同样,网格的疏密也影响程序的计算效率。本文采用网格自适应、当地模拟分子与真实分子比和动态时间步长[10-11]等优化方法来加快计算速度。
2.1 当地模拟分子与真实分子比DSMC方法中通过模拟分子代替真实分子,再利用模拟分子的运动状态得到流场的状态。所以,模拟分子的数量直接决定计算速度。为了保证流场的计算精度,在流场变化较大的区域都会进行网格加密。以往的全局模拟分子与真实分子比,会导致面积小的网格单元(即物面附近的单元,流场变化大)中模拟分子数少且计算不够精确,而面积大的网格单元(即远离物面的单元,流场变化小)中模拟分子数多计算耗时,浪费不必要的资源。
为了优化这一问题,本文采用当地模拟分子与真实分子比,即改变各单元中模拟分子所表示的真实分子数(后文称FNUM数)[12-14]的方法。基本思路是:每个网格单元根据其面积的大小采用不同的FNUM数(对于单元i,用CFNUM(i)表示)。通过得到的CFNUM(i)值确保每个网格单元中有相同的模拟分子数,从而保证了每个网格单元中有合适的模拟分子数。在计算过程中,分子进入不同的CFNUM(i)值的网格单元时,因其所代表的真实分子数不同采用删除或复制模拟分子的手段来实现流场量的平衡。
当地模拟分子与真实分子比方法的程序可以实现以下过程:
给定流场中最大面积网格单元的FNUM数,则各单元的CFNUM(i)值可以通过式(3)得到
| $CFNUM\left( i \right)=FNUM/{{S}_{max}}\times {{S}_{i}}$ | (3) |
式中Smax,Si分别为最大网格单元的面积和单元i的面积。
那么,各单元中所需投入的模拟分子数的求解公式为
| $NM=FND\times {{S}_{i}}/CFNUM\left( i \right)$ | (4) |
式中NM,FND分别为模拟分子数和分子数密度。
由式(3,4)可以得到
| $NM=FND\times {{S}_{max}}/FNUM$ | (5) |
从式(5)可以看到,各单元的模拟分子数与体积无关,仅由分子数密度决定。
2.2 动态时间步长技术分子的碰撞频率是:在单位时间内,分子的碰撞截面扫过的体积与流场的分子数密度的乘积,即ν=crπd2n,其中cr为分子的平均相对速度,从而可以得到分子的平均碰撞时间为t=1/ν=
不同密度区域的模拟分子平均碰撞时间不同,统一的时间步长降低了流场的计算速度。为了加快流场的时间发展历程,提高计算效率,对不同区域采用动态时间步长技术。
假设单元i的最大碰撞概率为Pi,max,最大运动速度为Vi,max。动态时间步长求解方法如下:
(1) 设定统一时间步长dt;
(2) 在N时间步长内(N为达到稳定时的指定时间步数),记录每个单元的最大碰撞概率Pi,max和最大运动速度Vi,max,并统计相应的平均值;
(3) 当达到稳定时间步数时,判断各单元的新时间步因子Ti,方法为:
① 记录原单元时间步长因子: Ti,old;
② 若Pi,max>Pmax,则新的时间步长因子为Ti,new=max(Ti,old-1,1);
③ 若Pi,max≤Pmax,则理想时间步长因子为Ti,new*=Hi/(Vi,max×dt),其中Hi=
(4) 经过步骤(1~3)的计算,在Ti×dt的时间间隔内,网格单元只需处理1次。
通过时间步长随时间的逐步变化,不仅加快了流场发展,更提高了计算效率。而非定常流动的计算要求单元物理时间步长一致,所以在求解非定常流动问题时,动态时间步长技术则不再适用。
3 算例与分析为了验证上述方法的正确性以及优化算法的计算效率,本文分别对高超声速圆柱绕流、二维扩张管道绕流进行数值模拟,并对数值结果进行了简单的分析比较。
3.1 高超声速圆球绕流通过程序对圆球进行基于切割单元的直角坐标网格生成,计算区域为(-0.03 m,0.03 m)×(-0.03 m,0.03 m),圆球的半径为0.01 m。为了方便比较,先后用不采用自适应网格与采用自适应网格的方法对算例进行计算。其中,初始网格单元数为2 312,网格节点数为2 546,如图 7所示。自适应加密后网格单元数为5 168,网格节点数为5 522,如图 8所示。上下左右4个边界均取为来流边界条件:来流为氮气,速度为2 000 m/s,气体温度297 K,物面温度300 K,来流分子数密度为1.0×1021。特征长度取圆球直径L=0.02 m,分子平均自由程λ=1.276 mm,计算得到努森数Kn=λ/L=0.063 8。计算中,采用VHS分子碰撞模型,平动能、转动能和振动能间的能量交换采用Larsen-Borgnakke统计模型[2, 15, 16],壁面反射采用完全漫反射模型。

|
图 7 未加密网格 Figure 7 Mesh without refinement |

|
图 8 自适应加密网格 Figure 8 Adaptive mesh refinement |
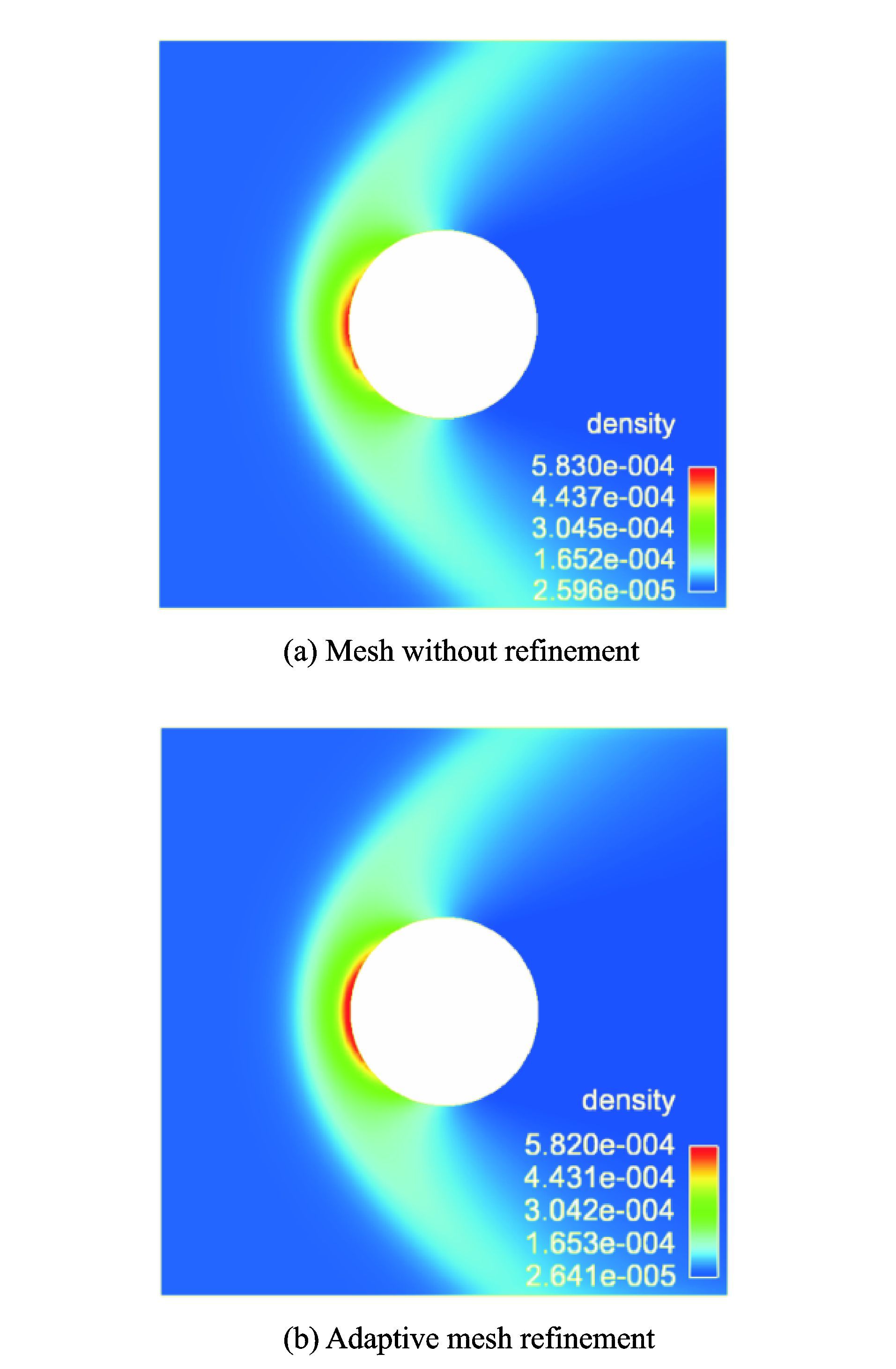
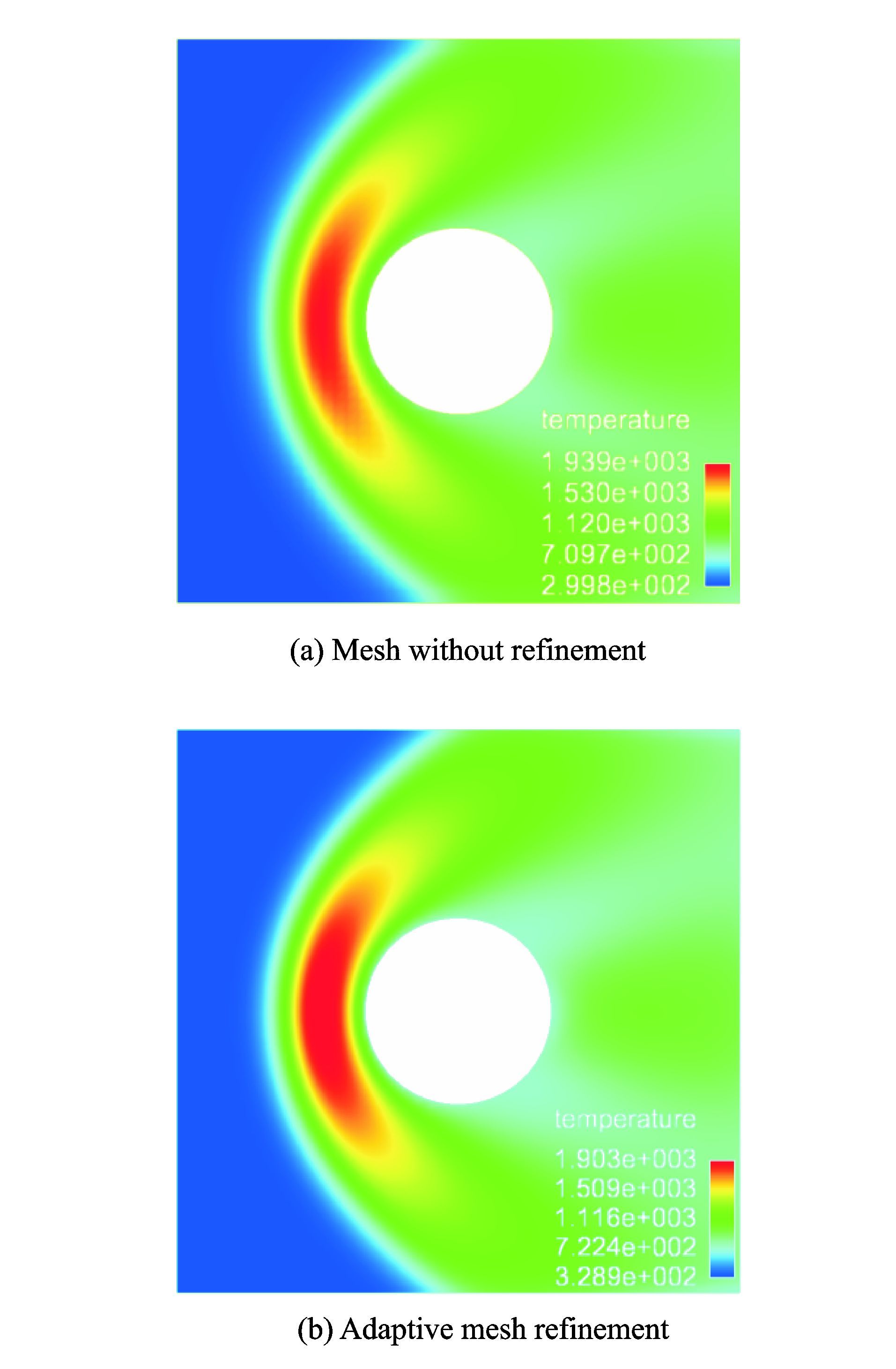
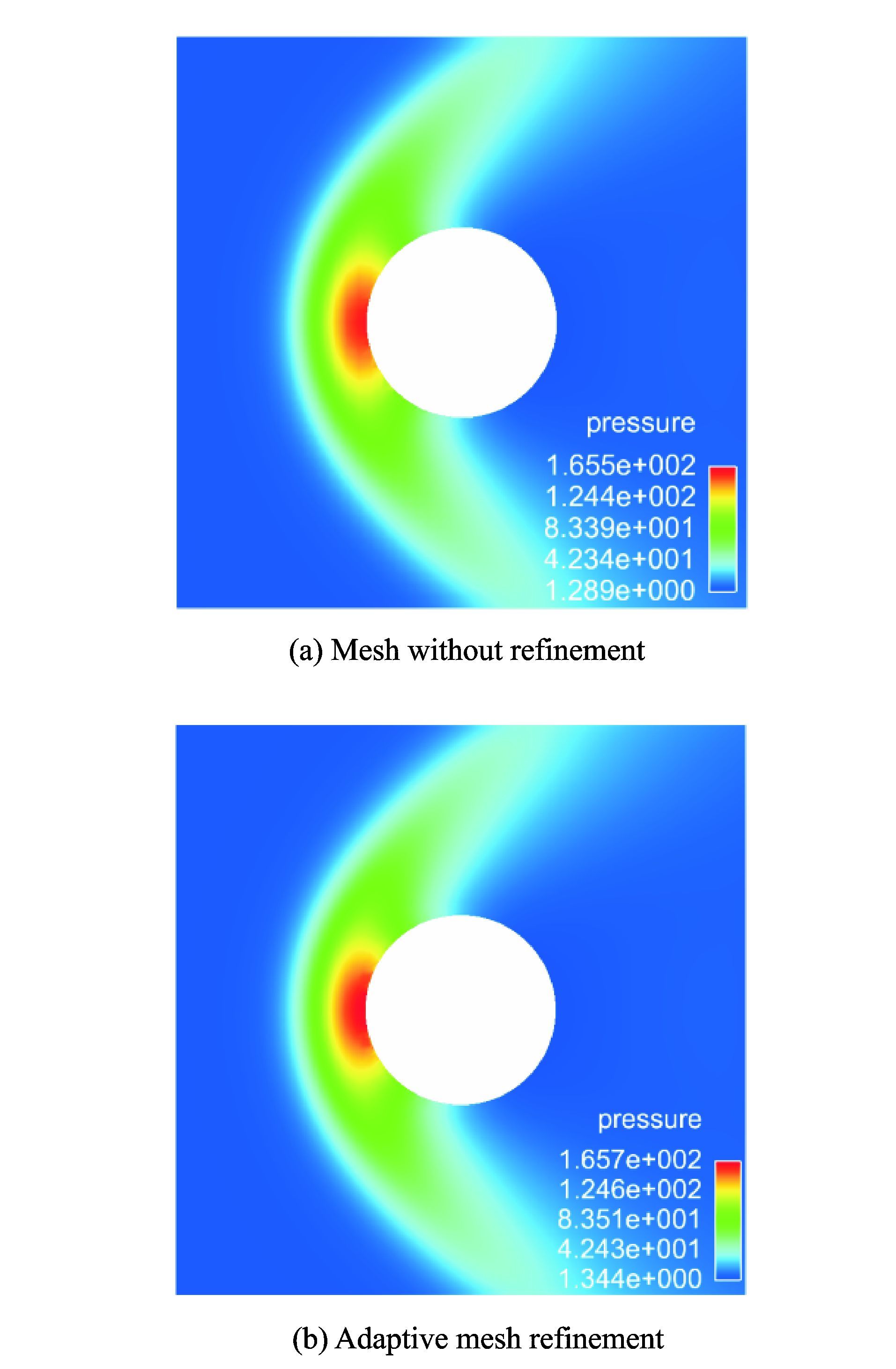
计算结果如图 9~11所示,分别为流场密度、温度和压力分布图。从图 9可以看出圆球头部出现明显的弓形脱体激波,在激波后气体的密度逐渐增加并在头部壁面处达到最大值。对比图 9(a,b)可以发现,经过自适应加密的网格计算所得到的结果能更好地捕捉圆球头部高密度区域。由图 10可知激波后气体的温度逐渐上升并达到最大值。值得注意的是,最大值并不在头部壁面处,原因在于壁面处的温度受到等温壁面条件的影响,其温度等于物面的温度。从图 11可以看出,激波后气体压力逐渐增大,在壁面处达到最大值,而沿着圆的表面朝向尾部逐渐减小。
|
图 9 圆球绕流计算的密度分布云图 Figure 9 Density distribution nephogram around sphere |
|
图 10 圆球绕流计算的温度分布云图 Figure 10 Temperature distribution nephogram around sphere |
|
图 11 圆球绕流计算的压力分布云图 Figure 11 Pressure distribution nephogram around sphere |
通过是否采用自适应网格的计算结果对比可以发现,经过自适应加密后的网格计算出的数值结果,不仅能够更加准确地捕捉到激波的位置,对高密度、温度和压强区域的捕捉也相当准确,同时流场变化也更加光顺。
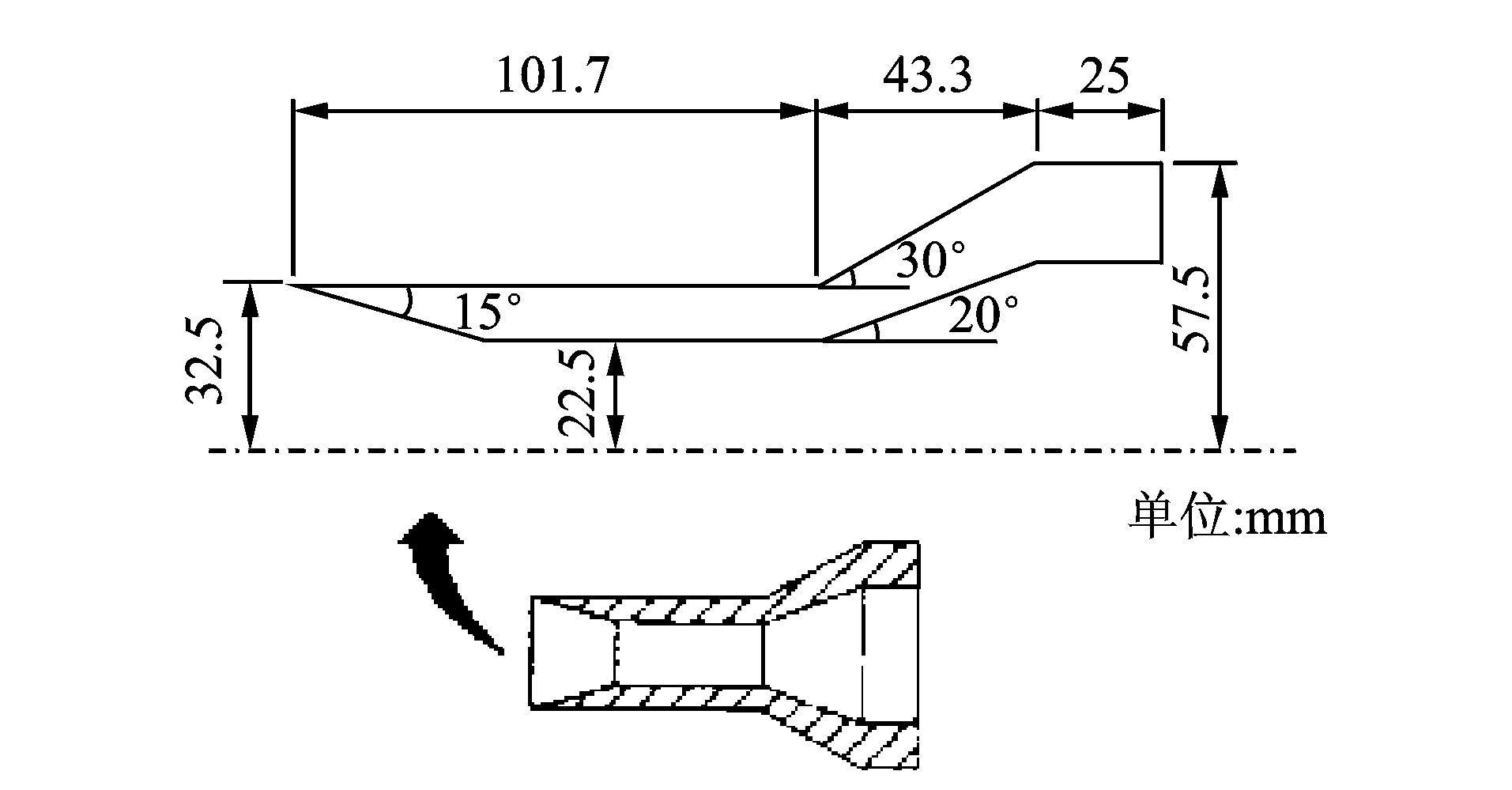
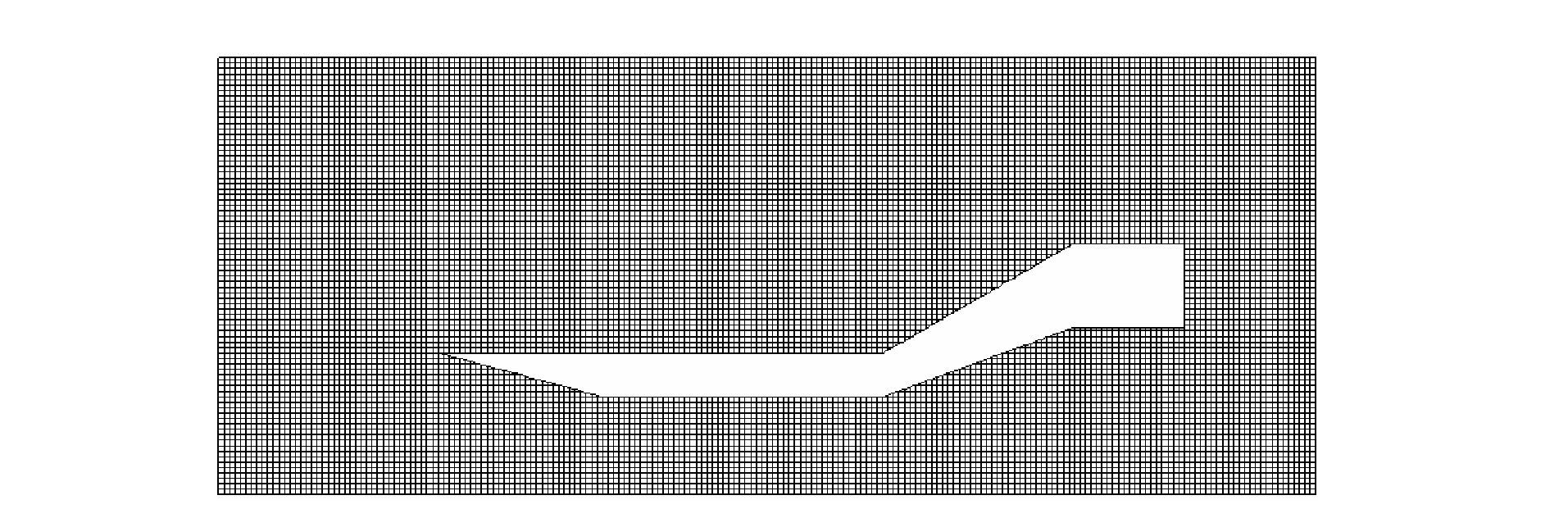
3.2 二维扩张管道绕流为了验证自适应直角坐标网格能生成适用于任意外形的直角坐标网格以及基于切割单元直角坐标网格的DSMC算法的正确性,本文对二维扩张管道模型[17-22]进行了数值模拟,管道的模型来自文献[17],如图 12所示。模型x方向上的长度为0.17 m,y方向上的宽度为0.035 m,前缘为15°倾斜角的尖前缘,管道内表面的扩张角度为20°,外表面的扩张角度为30°。因其外形是轴对称的,只需计算一半的流场。所以,计算区域取为(-0.05 m,0.20 m)×(0.00 m,0.10 m),其直角坐标网格如图 13所示,其中网格单元数77 861,网格节点数83 397,上边界以及左右边界取远场边界,下边界取为对称边界。通过数值结果,研究该模型表面的粘性干扰,尤其是在模型的前缘以及30°外倾斜坡附近的分离区域。
|
图 12 二维扩张管道几何结构 Figure 12 Geometry of expanding pipe |
|
图 13 二维扩张管道直角坐标网格 Figure 13 Cartesian mesh around expanding pipe |
来流气体为氮气、氧气组成的混合气体,其所占百分比为:0.763:0.237。来流速度为1 430 m/s,马赫数为9.9Ma,密度4.226×10-4 kg/m3,气体温度51.9 K,物面温度295 K,来流分子数密度为0.895×1022。特征长度取L=101.7 mm,分子平均自由程λ=0.1mm,计算得到努森数Kn=λ/L=0.001。计算中,采用VHS分子碰撞模型,平动能、转动能和振动能间的能量交换采用Larsen-Borgnakke统计模型,壁面反射采用完全漫反射模型。
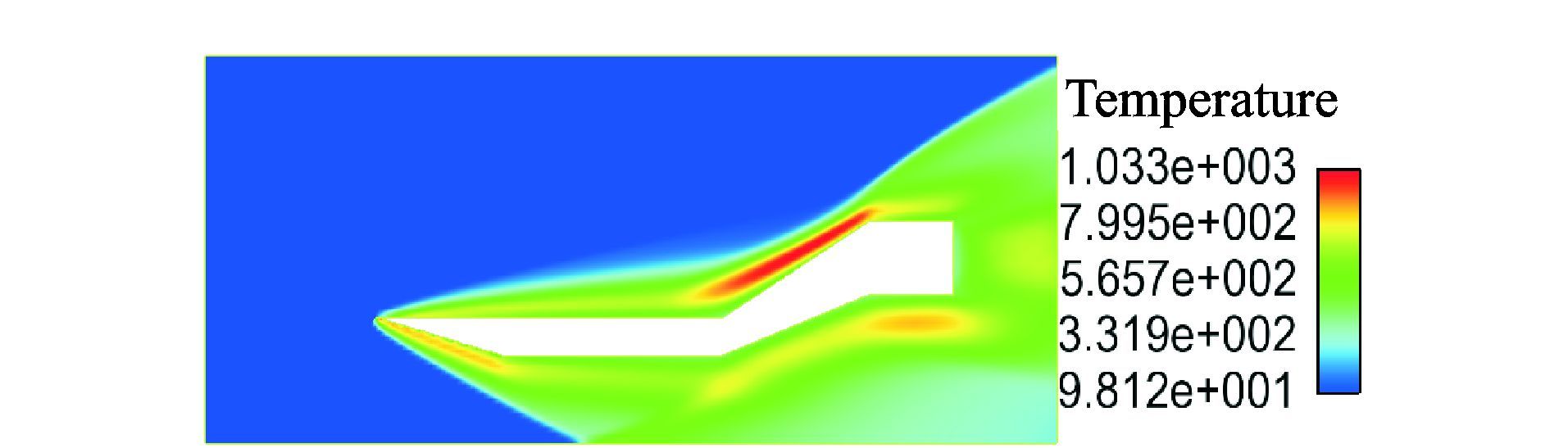
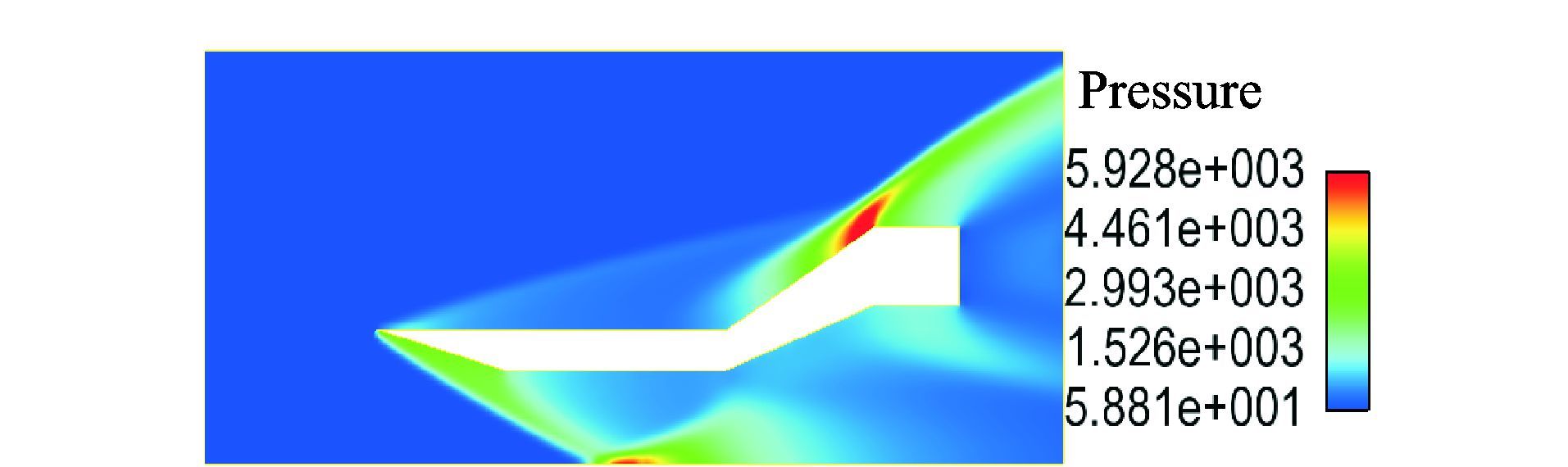
计算结果如图 14~16所示,分别为流场密度、温度和压力分布图。图 14中的密度分布可以看出由于模型前部为15°倾角尖前缘,产生了两道明显的斜激波。管道内部,斜激波碰到对称面后反射形成反射激波。此外,管道外压缩面也形成了一道斜激波。从图中可以看到斜激波与反射波的交界处以及管道外部两道斜激波的交界处都出现了高密度区。图 15~16中的温度和压力分布可以看出管道前缘15°倾斜面以及外部20°压缩面都为高温度和高压区域,并在压缩面中达到最大值。这都符合高超声速绕流的特点。

|
图 14 二维扩张管道高超声速绕流密度云图 Figure 14 Hypersonic density distribution nephogram around expanding pipe |
|
图 15 二维扩张管道高超声速绕流温度云图 Figure 15 Hypersonic temperature distribution nephogram around expanding pipe |
|
图 16 二维扩张管道高超声速绕流压力云图 Figure 16 Hypersonic pressure distribution nephogram around expanding pipe |
图 14~16中流场分布、激波位置、激波反射以及激波与激波的相交等流场特征均符合稀薄气体二维管道绕流情况。
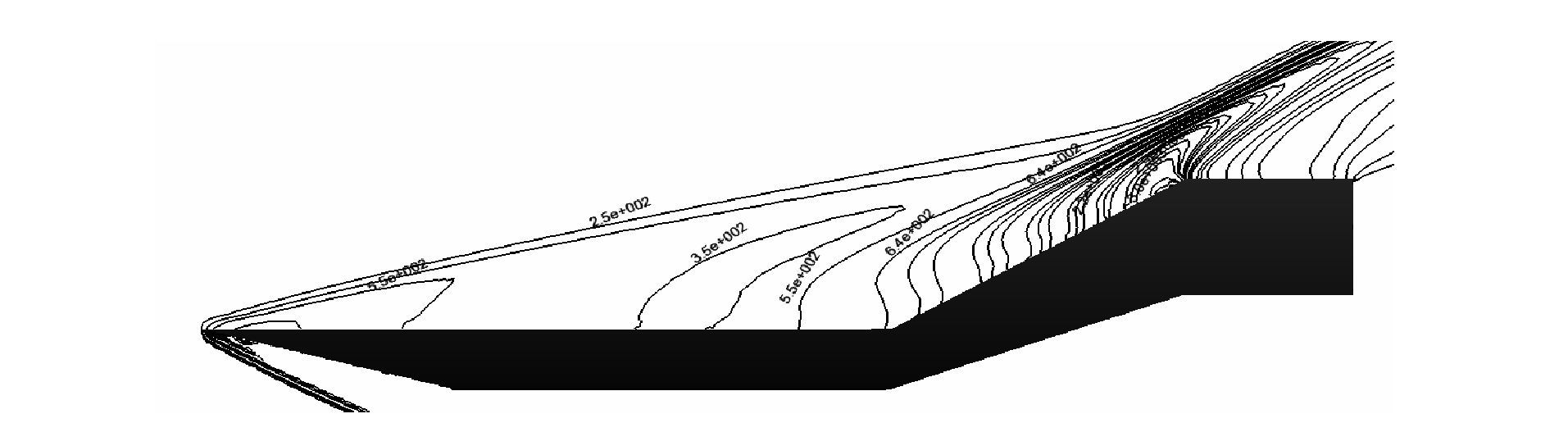
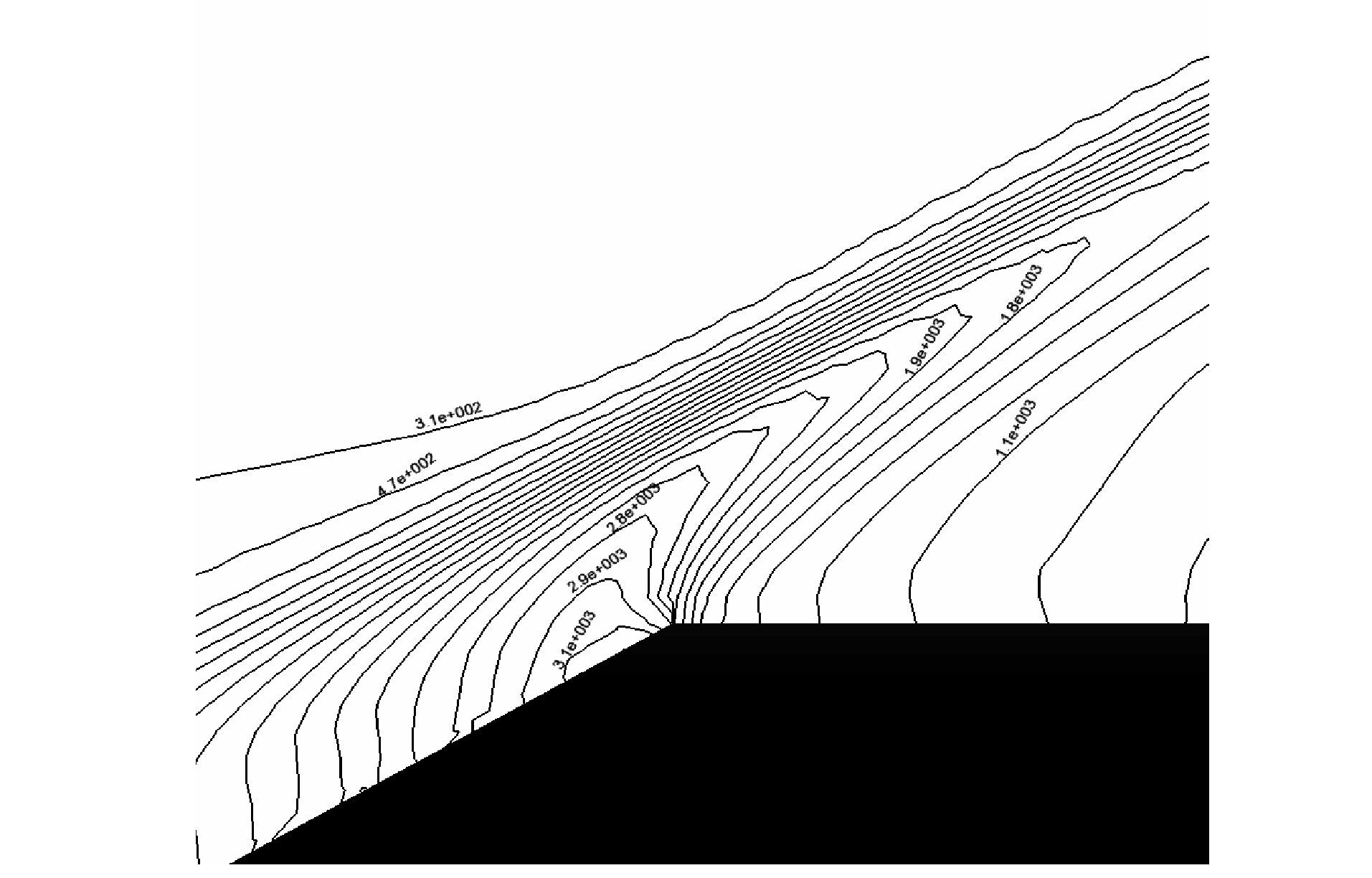
从图 17二维扩张管道上表面外侧流线分布图中可以看出气流分离的程度。从图 18~19二维扩张管道上表面压强等值线及压缩面附近局部放大等值线中可以看出激波的强度。

|
图 17 二维扩张管道上表面流线 Figure 17 Streamline around upper surface of expanding pipe |
|
图 18 二维扩张管道上表面压强等值线 Figure 18 Pressure isolines around upper surface of expanding pipe |
|
图 19 二维扩张管道压缩面附近压强等值线 Figure 19 Pressure isolines around compression surface of expanding pipe |
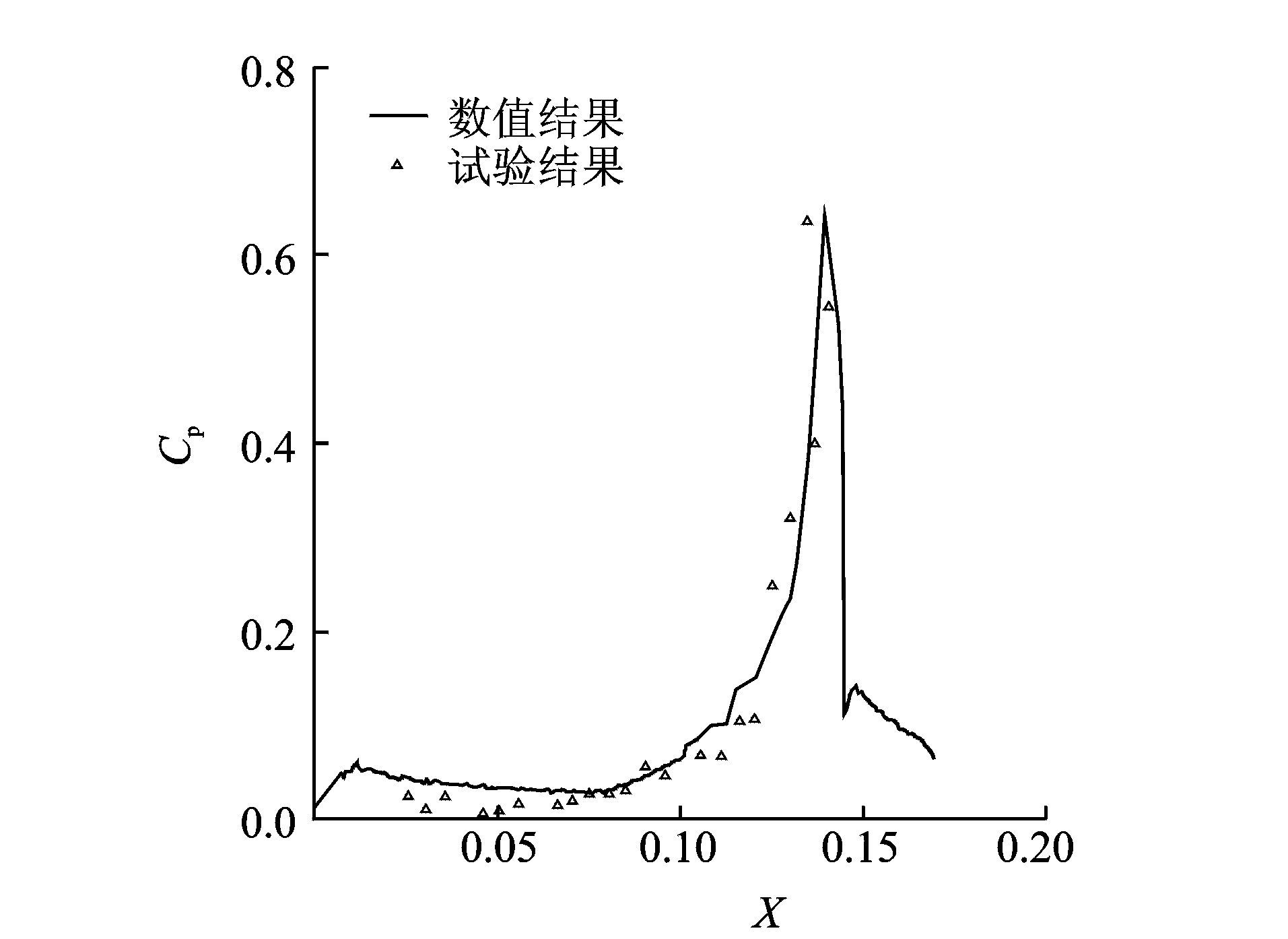
图 20为计算所得到的二维扩张管道外表面的压力系数Cp分布曲线,将数值结果与试验数据进行了对比,可以看出通过基于切割单元直角坐标网格的DSMC方法所得到的数值结果与文献[20]中的试验结果大致趋势一致。虽然对比结果存在着一定偏差,但是偏差都在合理范围内,也由此验证了方法的正确性。
|
图 20 外表面压力系数分布曲线 Figure 20 Pressure coefficient distribution curve around outside surface |
4 结束语
结合直角坐标网格与非结构网格各自的特点,本文提出了一种基于切割单元的直角坐标网格生成方法。通过这种方法能够对任意复杂外形几何结构进行快速的直角坐标网格生成,并对与物面相交的单元进行切割使单元贴体,其物面单元可以是任意形状,既保证了直角网格较高的计算效率,又能精确得到模拟物面附近的流动状态。同时,发展了基于切割单元直角坐标网格的DSMC方法,并通过当地模拟分子数、动态时间步长等优化措施提升计算效率。计算两组算例,先是通过高超声速圆球绕流的计算以及对比验证了直角坐标网格的生成方法和自适应加密方法的正确性,随后通过高超声速二维扩张管道数值模拟,观察二维扩张管道的激波位置以及流场特征验证DSMC方法的正确性。本文研究为发展三维情况下的基于切割单元直角坐标网格的DSMC方法打下了基础。
| [1] | Bird G A. Molecular gas dynamics and the direct simulation of gas flow[M]. Oxford: Clarendon Press, 1994 . |
| [2] |
沈青.
稀薄气体动力学[M]. 北京: 国防工业出版社, 2003 .
Shen Qing. Rarefied gas dynamics[M]. Beijing: National Defence of Industry Press, 2003 . |
| [3] |
樊菁.
DSMC位置元方法中的表面元的程序标识及分子表面发射确定论判据[J]. 力学学报 , 1999, 31 (6) : 671–675.
Fan Jing. Program making of surface element and the determination of molecular surface reflection in position element algorithm of DSMC method[J]. Chinese Journal of Theoretical and Applied Mechanics , 1999, 31 (6) : 671–675. |
| [4] |
朱自强.
应用计算流体力学[M]. 北京: 北京航空航天大学出版社, 1998 : 92 -124.
Zhu Ziqiang. Application of computational fluid mechanics[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 1998 : 92 -124. |
| [5] | Aftosmis M J, Berger M J, Melton J E. Robust and efficient cartesian mesh generation for component-based geometry [R]. AIAA Paper 97-0196, 1997. |
| [6] | Aftosmis M J. Solution adaptive Cartesian grid methods for aerodynamic flow with complex geometries[C]// 28th Computational Fluid Dynamics. Belgium:Van Kareman Insitute,1997. |
| [7] | Aftosmis M J, Berger M J, Melton J E. Adaptation and surface modeling for Cartesian mesh methods[J]. AIAA Paper 95-1725 , 1995 . |
| [8] |
罗运和, 戴青.
计算机图形学基础[M]. 北京: 中国计量出版社, 2003 : 80 -89.
Luo Yunhe, Dai Qing. Foundations of computer graphics[M]. Beijing: China Metrology Press, 2003 : 80 -89. |
| [9] |
王学德, 伍贻兆, 夏健.
二维非结构网格 DSMC 方法的实现及其应用[J]. 南京航空航天大学学报 , 2004, 36 (6) : 704–707.
Wang Xuede, Wu Yizhao, Xia Jian. Implementation of 2D unstructured DSMC method and its application[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2004, 36 (6) : 704–707. |
| [10] | Laux M. Local time stepping with automatic adaptation for the DSMC method [R]. AIAA Paper 98-2670, 1998. |
| [11] |
杜永乐, 阎超.
DSMC方法中得自适应当地时间步长法[J]. 北京航空航天大学学报 , 2006, 32 (4) : 387–390.
Du Yongle, Yan Chao. Adaptive local time step method for DSMC code[J]. Journal of Beijing University of Aeronautics and Astronautics , 2006, 32 (4) : 387–390. |
| [12] |
陈作斌.
计算流体力学及应用[M]. 北京: 国防工业出版社, 2003 : 273 -294.
Chen Zuobin. Computational fluid dynamics and application[M]. Beijing: National Defence of Industry Press, 2003 : 273 -294. |
| [13] | Wilmoth R G, Carlson A B, LeBeau G J. DSMC grid methodologies for computing low-density, hypersonic flows about reusable launch vehicles [R]. AIAA Paper 96-1812, 1996. |
| [14] | LeBeau G J. A parallel implementation of the direct simulation monte Carlo method[J]. Computer Methods in Applied Mechanics and Engineering , 1999 (174) : 319–337. |
| [15] | Bergnakke C, Larsen P S. Statistical collision model for Monte Carlo simulation of poly-atomic gas mixture[J]. Journal of Computational Physics , 1975, 18 (4) : 405–420. DOI:10.1016/0021-9991(75)90094-7 |
| [16] | Ivanov M S, Markelov G N, Gimelshein S F. Statistical simulation of reactive rarefied flows: Numerical approach and applications [R]. AIAA Paper 98-2669, 1998. |
| [17] | Moss J N, Dogra V K, Price J M. DSMC simulation of viscous interactions for a hollow Cylinder-Flare confirguration [R]. AIAA Paper 94-2015, 1994. |
| [18] | Moss J N, Price J M, Dogra V K,et al. Comparison of DSMC and experimental results for hypersonic external flows [R]. AIAA Paper 95-2028, 1995. |
| [19] | Moss J N, Olejniczak J. Shock-wave/boundary-layer interactions in hypersonic low density flows [R]. AIAA Paper 98-2668, 1998. |
| [20] | Chanetz B. Study of axi-symmetric shock wave boundary layer interaction in hypersonic laminar flow [R]. ONERA Technical Report RT 42/4362 AN, 1995. |
| [21] | Kim M G, Kim S H, Kwon O. J. A parallel cell-based DSMC method with dynamic load balancing using unstructured adaptive meshes [R]. AIAA Paper 2003-1033, 2003. |
| [22] | Markelov G N, Kudryavtsev A N. Continuum and kinetic simulation of laminar separated flow at hypersonic speed[J]. Journal of Spacecraft and Rockets , 2000, 37 (4) : 499–506. DOI:10.2514/2.3591 |
 2016, Vol. 48
2016, Vol. 48


