2. 上海飞机设计研究院,上海,201210
2. Shanghai Aircraft Design and Research Institute, Shanghai, 201210, China
物-伞系统航迹及姿态对于减速系统性能评估十分重要,物-伞系统运动动力学问题一直是降落伞研究领域非常重要的内容。自20世纪60年代开始至今,国内外有非常多的学者都致力于物-伞动力学建模及分析工作[1]。早期工程中最常用的模型为二自由度模型[2-3],将物伞系统视为集中在物伞系统质心处的一个质点,并假定质点做平面运动,质点的质量为物伞系统质量与降落伞的附加质量之和。然后Wolf建立了物伞系统5自由度(忽略滚转运动)的三维刚体模型[4],Tory和Ayres描述了一个6自由度的物伞系统运动模型[5],其中假设伞和回收物是刚性连接的。再然后,为了得到更多的信息,将物-伞系统作为两体或三体对象,并逐渐出现了9自由度、12自由度甚至27自由度模型。Doherr和Schilling在研究旋转伞-弹药系统的运动轨迹和动力学行为时开发了一个9自由度计算程序[1]。金友兵等采用这种方法建立了鱼雷和伞系统9自由度空中运动模型[6],通过选取独立的伪速度,伞和鱼雷之间的相互作用力自动消去。Talay提出一个12自由度的物伞系统运动模型[7],伞和回收物各有6个自由度。伞绳用无质量的弹簧一阻尼模型来模拟,吊带用无质量的弹簧来模拟,在伞绳和吊带的汇交点处满足力的静平衡条件。Pillasch针对旋转伞-弹药系统,建立了10自由度与15自由度模型[8]:10自由度模型中包含了个物体伞-扩展器-摩擦盘-摆臂-弹药,后面4个物体用3个转动幅连接起来;在15自由度模型中,假设悬挂扩展器的伞绳是阻尼弹性的,作者利用拉格朗日方程方法推导了系统的运动方程。在Nikraversh的多体动力学文献中,对同样的系统提出了一个27自由度模型[9]。郭叔伟等利用各个模型对同一物伞系统对象进行仿真计算[10],通过比较不同自由度物伞系统动力学模型下的计算结果,得出不同自由度模型的差异、特点以及应用范围和计算所需初始条件。上述方法均将降落伞视为单一刚体或质点,这种简化对物-伞系统的模拟带来了一定的误差。
为得到更准确的结果,本文将伞系统离散为质点系,根据质点系动量定理和动量矩定理在降落伞质心处推导出一种改进的降落伞动力学模型。物-伞系统为12自由度模型,易于编程,且降落伞的质量分布体现在了模型方程中,能对降落伞的动力学进行更准确的模拟。
1 降落伞质点系动力学模型模拟降落伞稳降阶段的传统模型大多将降落伞简化为一个刚体,并在降落伞质心处作用动量和动量矩。本文将伞系统离散为n个质点,其模型如图 1所示。降落伞体坐标原点ot选取在压力中心oq,相比刚体质心动力学方程,使附加质量矩阵和附加质量惯性矩矩阵简化为对角矩阵[10]。(oxyz)d为地面坐标系;(oxyz)t为降落伞的体坐标系。oi为伞系统某质点i的质心;ρi为此质心在体坐标系下的矢径。 设降落伞各质点质量为mi(i=1,2,…,n),则各质点质量占降落伞总质量(ms=
| ${{\rho }_{s}}=\sum\limits_{i=1}^{n}{{}}{{\mu }_{i}}{{\rho }_{i}}$ | (1) |

|
图 1 降落伞模型 Figure 1 Parachute model |
1.1 降落伞质点系运动方程
见图 1,在地面坐标下降落伞质心的矢径rs为
| ${{r}_{s}}={{r}_{t}}+{{\rho }_{s}}={{r}_{t}}+\sum\limits_{i=1}^{n}{{}}{{\mu }_{i}}{{\rho }_{i}}$ | (2) |
对式(2)求二阶导数,即得到降落伞质心的绝对加速度
| $\frac{{{d}^{2}}{{r}_{s}}}{d{{t}^{2}}}=\frac{{{d}^{2}}{{r}_{t}}}{d{{t}^{2}}}+\sum\limits_{i=1}^{n}{{}}{{\mu }_{i}}\frac{{{d}^{2}}{{\rho }_{i}}}{d{{t}^{2}}}$ | (3) |
由牛顿第二定律得
| $\frac{{{d}^{2}}{{r}_{s}}}{d{{t}^{2}}}~=\frac{{{d}^{2}}{{r}_{t}}}{d{{t}^{2}}}+\sum\limits_{i=1}^{n}{{}}{{\mu }_{i}}~\frac{{{d}^{2}}~{{\rho }_{i}}}{d{{t}^{2}}}=F/{{M}_{s}}$ | (4) |
式中Ms,F分别为降落伞的质量矩阵及合外力矩阵,F表达式为
| $F = B_t^d\left[ \matrix{ {Q_n} \hfill \cr {Q_t} \hfill \cr {Q_z} \hfill \cr} \right] + \left[ \matrix{ 0 \hfill \cr G \hfill \cr 0 \hfill \cr} \right] + B_T^d\left[ \matrix{ 0 \hfill \cr - T \hfill \cr 0 \hfill \cr} \right]$ | (5) |
式中:Qn,Qt,Qz分别为降落伞法向、切向、副法向气动力,即体坐标系下x,y,z方向气动力;G为降落伞重力;T为连接在降落伞下方的吊带张力;Btd,BTd分别为降落伞体坐标系、吊带体坐标系与地面坐标系的转换矩阵。
根据体坐标系(旋转坐标系)下任意矢量的求导法则,矢径ρ的二阶导数为
| $\frac{{{d}^{2}}\rho }{d{{t}^{2}}}=\frac{{{\partial }^{2}}\rho }{\partial {{t}^{2}}}+\frac{d\omega }{dt}\times \rho +\omega \times \left( \omega \text{ }\times \rho \right)+2\omega \times \frac{\partial \rho }{\partial t}$ | (6) |
式中ω为体坐标系相对于地面坐标的牵连角速度。在降落伞充气完成后,可认为降落伞形状不变,即降落伞各质心位置在体坐标系的矢径不变,则式(6)简化为
| $\frac{{{d}^{2}}\rho }{d{{t}^{2}}}=\frac{d\omega }{dt}\times \rho +\omega \times \left( \omega \text{ }\times \rho \right)$ | (7) |
将式(7)代入式(4),即得到地面坐标系下降落伞的质点系动力学方程
| $\frac{{{d}^{2}}{{r}_{t}}}{d{{t}^{2}}}F/{{M}_{s}}~-\sum\limits_{i=1}^{n}{{}}{{\mu }_{i}}\left( \frac{d\omega }{dt}\times {{\rho }_{i}}+\omega \text{ }\times \left( \omega \times {{\rho }_{i}} \right) \right)$ | (8) |
式中
| ${{M}_{s}}=\left[ \begin{matrix} {{m}_{s}}+{{m}_{f.x}} & 0 & 0 \\ 0 & {{m}_{s}}+{{m}_{f.y}} & 0 \\ 0 & 0 & {{m}_{s}}+{{m}_{f.z}} \\ \end{matrix} \right]$ | (9) |
式中:ms为降落伞质量;mf.x,mf.y,mf.z分别为降落伞x,y,z方向的附加质量,表达式为
| $\begin{align} & {{m}_{f.y}}=\frac{{{\rho }_{a}}{{R}_{t}}}{{{C}_{t}}}{{C}_{A}}~-0.367{{\rho }_{a}}{{\left( \frac{{{C}_{A}}}{{{C}_{t}}} \right)}^{1.5}} \\ & {{m}_{f.x}}={{m}_{f.z}}=0.5{{m}_{f.y}} \\ \end{align}$ | (10) |
式中:Rt为降落伞投影半径;ρa为空气密度;Ct为降落伞切向气动力系数;CA为降落伞阻力面积。
1.2 降落伞质点系转动方程降落伞体轴坐标系下的转动动力学方程为
| $\frac{d{{H}_{{{o}_{q}}}}}{dt}=\frac{\delta H{{~}_{{{o}_{q}}}}}{\delta t}~+\omega \times {{H}_{{{o}_{q}}}}={{M}_{{{o}_{q}}}}$ | (11) |
降落伞绕压力中心的动量矩Hoq为
| $\begin{array}{*{35}{l}} {{H}_{{{o}_{q}}}}=\sum\limits_{i=1}^{n}{{}}\left( {{\rho }_{i}}\times {{m}_{i}}{{v}_{i}} \right)=\sum\limits_{i=1}^{n}{{}}{{I}_{i-o}}\times \omega = \\ I{{~}_{s}}+{{I}_{f}}\times \omega =I_{s}^{*}\times \omega \\ \end{array}$ | (12) |
式中Is,If分别为降落伞的转动惯量及附加惯量矩阵。
降落伞气动力矩Moq为
| ${M_{{o_q}}} = {\rho _n} \times B_T^t\left[ \matrix{ 0 \hfill \cr - T \hfill \cr 0 \hfill \cr} \right] + {\rho _s} \times B_d^t\left[ \matrix{ 0 \hfill \cr G \hfill \cr 0 \hfill \cr} \right] + {\rm{ }}{M_q}$ | (13) |
式中:BTt为吊带体坐标系与降落伞体坐标系的转换矩阵;Bdt为地面坐标系与降落伞体轴坐标系间的转换矩阵;Mq为气动力矩。
将式(12)代入式(11),并化简可得到降落伞转动方程
| $\frac{d\omega }{dt}={{({{I}_{s}})}^{-1}}\times \left( {{M}_{{{o}_{q}}}}~-\omega \right)\times \left( I_{s}^{*}\times \omega \right)$ | (14) |
式中
| ${{I}_{s}}=\left[ \begin{matrix} {{I}_{s.x}}+{{I}_{f.x}} & 0 & 0 \\ 0 & {{I}_{s.y}}+{{I}_{f.y}} & 0 \\ 0 & 0 & {{I}_{s.x}}+{{I}_{f.z}} \\ \end{matrix} \right]$ | (15) |
式中If.x,If.y,If.z分别为降落伞x,y,z方向的附加转动惯量
| $\begin{align} & {{I}_{f.y}}~=\text{ }0.063{{\rho }_{a~}}R_{i}^{5} \\ & {{I}_{f.x}}~=\text{ }{{I}_{f.z~}}=\text{ }0.042{{\rho }_{a~}}R_{i}^{5} \\ \end{align}$ | (16) |
式中Ri为伞衣底边进口半径。
2 载荷刚体质心动力学模型载荷在地面坐标系下的运动方程为
| ${m_p}{d \over {dt}}\left[ \matrix{ {v_{px}} \hfill \cr {v_{py}} \hfill \cr {v_{pz}} \hfill \cr} \right]B_p^dB_q^p\left[ \matrix{ - D \hfill \cr L \hfill \cr 0 \hfill \cr} \right] + \left[ \matrix{ 0 \hfill \cr - {m_p}g \hfill \cr 0 \hfill \cr} \right] + B_T^p\left[ \matrix{ 0 \hfill \cr T \hfill \cr 0 \hfill \cr} \right]$ | (17) |
式中:Bpd为载荷体坐标系到地面坐标系的转换矩阵;Bqp为气动坐标系到载荷体坐标系的转换矩阵;BTp为吊带体坐标系到载荷体坐标系的转换矩阵;D为载荷的阻力;L为载荷的升力;mp为载荷的质量。
载荷在地面坐标系下的转动方程为
| ${d \over {dt}}\left[ \matrix{ {\omega _{px}} \hfill \cr {\omega _{py}} \hfill \cr {\omega _{pz}} \hfill \cr} \right] = {\left[ {\matrix{ {{I_{px}}} & 0 & 0 \cr 0 & {{I_{py}}} & 0 \cr 0 & 0 & {{I_{pz}}} \cr } } \right]^{ - 1}} \times {\rm{ }}\left( {\left[ \matrix{ {M_{px}} \hfill \cr {M_{py}} \hfill \cr {M_{pz}} \hfill \cr} \right] - \left[ \matrix{ {H_x} \hfill \cr {H_y} \hfill \cr {H_z} \hfill \cr} \right]} \right)$ | (18) |
式中Hx,Hy,Hz为载荷在地面坐标系x,y,z方向上的动量矩,表达式为
| $\left[ \matrix{ {H_x} \hfill \cr {H_y} \hfill \cr {H_z} \hfill \cr} \right] = \left[ {\matrix{ 0 & { - {\omega _z}} & {{\omega _y}} \cr {{\omega _z}} & 0 & { - {\omega _x}} \cr { - {\omega _y}} & {{\omega _x}} & 0 \cr } } \right]\left[ {\matrix{ {{I_{px}}} & 0 & 0 \cr 0 & {{I_{py}}} & 0 \cr 0 & 0 & {{I_{pz}}} \cr } } \right]\left[ \matrix{ {\omega _x} \hfill \cr {\omega _y} \hfill \cr {\omega _z} \hfill \cr} \right]$ | (19) |
Mpx,Mpy,Mpz为载荷在地面坐标系x,y,z方向上的外力矩,表达式为
| $\left[ \matrix{ {M_{px}} \hfill \cr {M_{py}} \hfill \cr {M_{pz}} \hfill \cr} \right] = {1 \over 2}{\rho _a}u_p^2{\left( {AD} \right)_p}\left[ \matrix{ {C_{mx}} \hfill \cr {C_{my}} \hfill \cr {C_{mz}} \hfill \cr} \right] + {r_{OA}} \times B_d^pB_T^p\left[ \matrix{ 0 \hfill \cr T \hfill \cr 0 \hfill \cr} \right]$ | (20) |
式中:Cmx,Cmy,Cmz为载荷在地面坐标下x,y,z方向上的气动力矩系数;(AD)p为载荷的特征面积和特征直径;rOA为载荷体坐标系原点到吊带连接点的矢径。
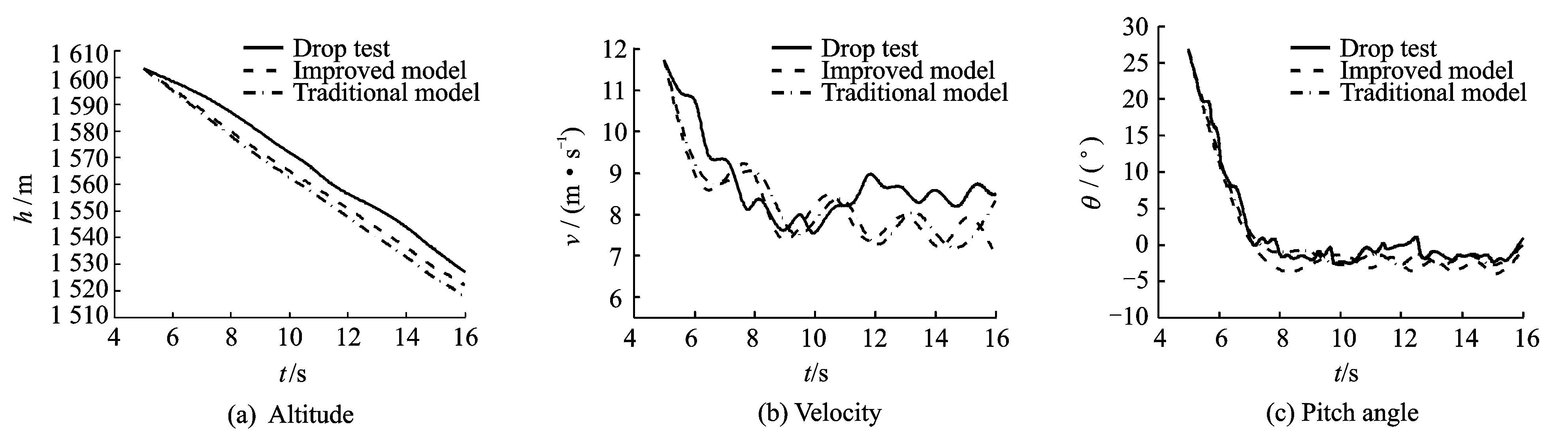
3 算例验证为验证本文模型的正确性,本文基于Matlab平台,自编程序,采用四阶龙格-库塔方法对文献[11]中的十字形伞的稳降阶段进行模拟(其主要设计参数见表 1),得到位移、速度、欧拉角随时间的变化曲线。同时将改进模型与空投实验的结果进行对比,如图 2所示。结果表明数值计算结果和空投试验结果符合较好,表明这种模型具有较好的可靠性。
| 表 1 十字形降落伞主要设计参数 Table 1 Main design parameters of cruciform parachute |
|
图 2 试验结果与模拟结果对比 Figure 2 Comparison of experimental and simulation results |
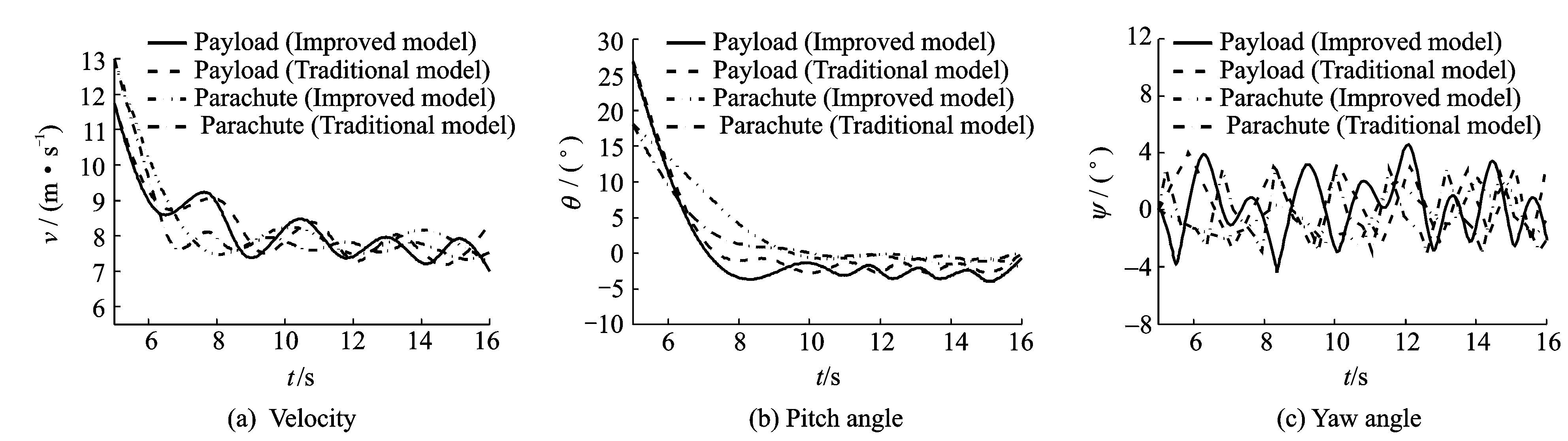
图 3为模拟所得降落伞和载荷体的速度、俯仰角、偏航角计算结果,降落伞的俯仰角和偏航角振荡幅度约为2°,4°,载荷的俯仰角和偏航角振荡幅度约为3°,8°,由于伞绳的弹性作用,降落伞和载荷的速度平均值在稳降阶段逐渐降为8 m/s左右振荡,波幅分别约为1.0和0.8 m/s。由图 3可知,传统模型[7]和改进模型所得负载结果的幅值、均值和振荡频率相近,而且两者所得的降落伞结果幅值和均值也相近,两者的差别主要在于采用改进模型的降落伞振荡频率较小,而传统模型的振荡频率较大,与负载的振荡频率相近。在工程实际中,降落伞的振荡频率应为载荷频率的0.5倍以下,可见通过采用质点系模型,改进模型相对于传统模型能得到更准确的降落伞振荡频率。
|
图 3 降落伞与载荷体运动情况 Figure 3 Movement of parachute and payload |
4 结束语
本文根据质点系动量定理和动量矩定理推导出一种新的降落伞动力学模型,基于此模型对某十字型伞稳降阶段进行了编程计算,计算结果与空投实验基本一致。对模拟所得降落伞及载荷体的运动速度和姿态角度进行了对比分析,降落伞和载荷的速度平均值在稳降阶段逐渐趋于一致,降落伞的欧拉角相较于载荷振荡频率较小,变化范围较小。本文方法编程简单,具有较好的可靠性,相较于传统模型能得到更准确的降落伞速度和姿态角的振荡频率,是伞-载系统动力学模型的有益补充。
| [1] | Dohher K F, Schilling H. Nine-degree-of-freedom simulation of rotating parachute systems[J]. J Aircraft , 1992, 29 (5) : 774–780. DOI:10.2514/3.46245 |
| [2] | White F M, Wolf D F. A theory of three dimensional parachute dynamic stability[J]. J Aircraft , 1968, 5 (1) : 86–92. DOI:10.2514/3.43912 |
| [3] |
李大耀, 李大治.
物体-双伞系统运动方程与稳定性判据[J]. 宇航学报 , 1997, 18 (4) : 93–97.
Li Dayao, Li Dazhi. Motion equations and stability criteria of body-biparachutes system[J]. Journal of Astronautics , 1997, 18 (4) : 93–97. |
| [4] | Wolf D F. The dynamic stability of a nonrigid parachute and payload system [D]. Kingston:University of Rhode Island, 1968. |
| [5] | Tory T, Ayres R. Computer model of a fully deployed parachute[J]. J Aircraft , 1977, 14 (7) : 675–679. DOI:10.2514/3.58839 |
| [6] |
金友兵, 邵大燮, 薛晓中, 等.
鱼雷和伞的空中运动模型[J]. 弹道学报 , 1998, 10 (2) : 87–92.
Jin Youbing, Shao Daxie, Xue Xiaozhong, et al. The air motion model of the torpedo and the parachute[J]. Journal of Ballistics , 1998, 10 (2) : 87–92. |
| [7] | Talay T A .Parachute-deployment-parameter identification based on an analytical simulation of Viking BLDT AV-4[R].NASA TN D-7678,1974. |
| [8] | Pillasch D W, Shen Y C, Valero N. Parachute sub munition system coupled dynamics [R]. AIAA Paper 84-0784, 1984. |
| [9] | Nikravesh P E. Dynamic analysis of large-scale mechanical systems and animated graphics[J]. J Guidance , 1985, 8 (1) : 104–109. DOI:10.2514/3.19941 |
| [10] |
郭叔伟, 董杨彪, 秦子增.
物伞系统动力学模型和讨论[J]. 航天返回与遥感 , 2008, 29 (3) : 38–44.
Guo Shuwei, Dong Yangbiao, Qin Zizeng. Dynamic model and discussion of the parachute and payload system[J]. Spacecraft Recovery & Remote Sensing , 2008, 29 (3) : 38–44. |
| [11] |
贾华明, 李健.
收口十字形降落伞充气过程动力学建模与仿真[J]. 航天返回与遥感 , 2012, 33 (5) : 16–23.
Jia Huaming, Li Jian. Modeling and simulation of inflation process dynamics of reefed cruciform parachute[J]. Spacec Raftrecovery & Remote Sensing , 2012, 33 (5) : 16–23. |
 2016, Vol. 48
2016, Vol. 48


