2. 上海飞机设计研究院,上海,201210
2. Shanghai Aircraft Design and Research Institute, Shanghai, 201210, China
降落伞具有折叠体积小、质量轻及减速效果好等优点,在航空、航天、航海、兵器和救生等诸多领域得到广泛的应用。降落伞和各类载荷对象构成了复杂的伞-载飞行体,其开伞可靠性是伞-载飞行系统最为关心的问题,由于开伞失败导致物毁人亡的事故至今还屡屡发生。降落伞的开伞过程包括两个阶段:拉直阶段和充气阶段。为了保障开伞安全,良好有序的拉出过程是开伞的基础[1-2]。研制人员在对降落伞失效案例[2-4]的分析中,发现很多问题都是因降落伞拉出过程出现问题造成。主要表现在以下3个方面:
(1) 降落伞拉出过程与主伞包或载荷体轴向存在较大夹角,引起降落伞与主伞包(或载荷体)高速摩擦,造成灼伤损伤或织物撕裂。
(2) 拉出过程中拉直力过大,伞绳直接拉断造成伞-载系统分离。
(3) 拉直过程中柔性降落伞出现绳帆弯曲等现象,造成充气过程伞顶甩打或非对称充气,导致伞衣应力局部过大,造成伞衣破损。
降落伞拉出过程非常迅速,短时间内会完成一系列物理动作。为了减小降落伞拉出过程中的拉直力,伞衣常常采用扎紧带固定,因此正在拉出的伞系统阻力面积无明显变化。根据上述特点,降落伞拉出过程往往忽略了载荷体尾流的影响,伞系统被认为是质量分布不等的绳索系统,基于绳索动力学理论形成了一系列降落伞拉出过程理论模型。早期降落伞拉直过程动力学模型多为简单的直线拉出模型[5-8],后来由于研究问题的需要,出现了复杂的多质点多刚体模型[1, 9-13]。通过对上述模型的仿真求解可以预测出载荷、伞包的相对运动情况及拉直力变化情况。
本文根据柔性降落伞拉出过程的重要特征,以绳索动力学为基础,综述了降落伞拉直过程动力学仿真分析的一些方法及其特点,构建了动力学模型中主要因素之间的相互关系,分析了绳段张力的几种计算模型及其特点,提出了伞-载系统拉直过程仿真技术未来需要关注的几方面问题。
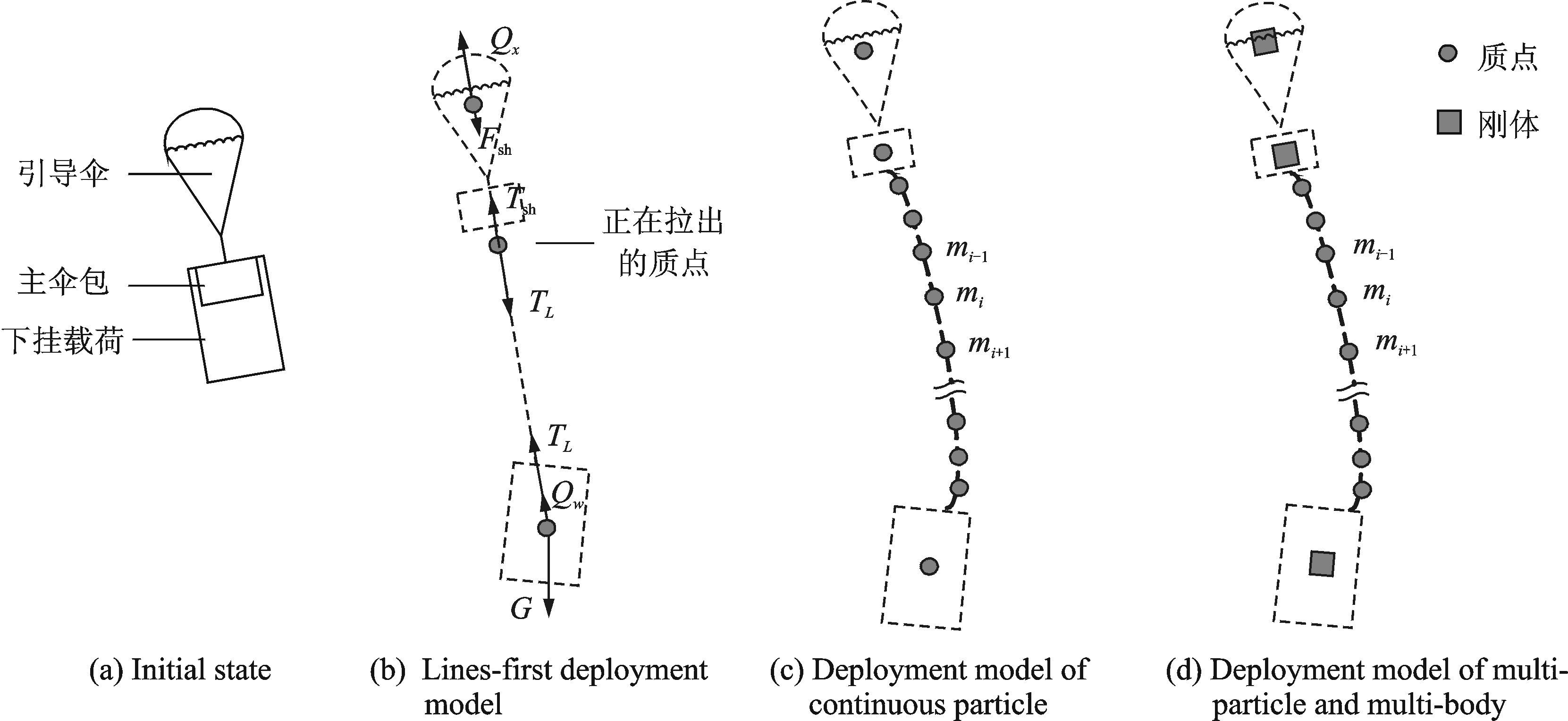
1 动力学模型及特点拉出过程是伞包内折叠状态的伞衣和伞绳逐渐拉出的过程(图 1),也是主伞包内质量不断减少的变质量问题,分为先拉伞衣法(顺拉法)和先拉伞绳法(倒拉法)两种情况。一般而言倒拉法的最大拉直力要小于顺拉法,故大多数降落伞采用倒拉方法开伞。根据研究问题的需要,拉直过程动力学仿真模型主要有:(1)平面直线拉出模型;(2)多质点连续拉出模型;(3)多质点多刚体非连续拉出模型。
|
图 1 降落伞拉直模型 Figure 1 Deployment model of parachute |
早期研究采用的是平面直线拉出模型(以下简称模型A),该方法假设拉出过程伞绳伞衣始终保持为平面直线状态,将引导伞与伞包、下挂载荷与拉出部分视为两个变质量控制体,基于牛顿力学定律建立了两体变质量系的运动动力学方程,通过求解拉直过程中引导伞(含伞包)与下挂载荷之间相对位置的变化,求解拉直力和拉出时间[5-8]。
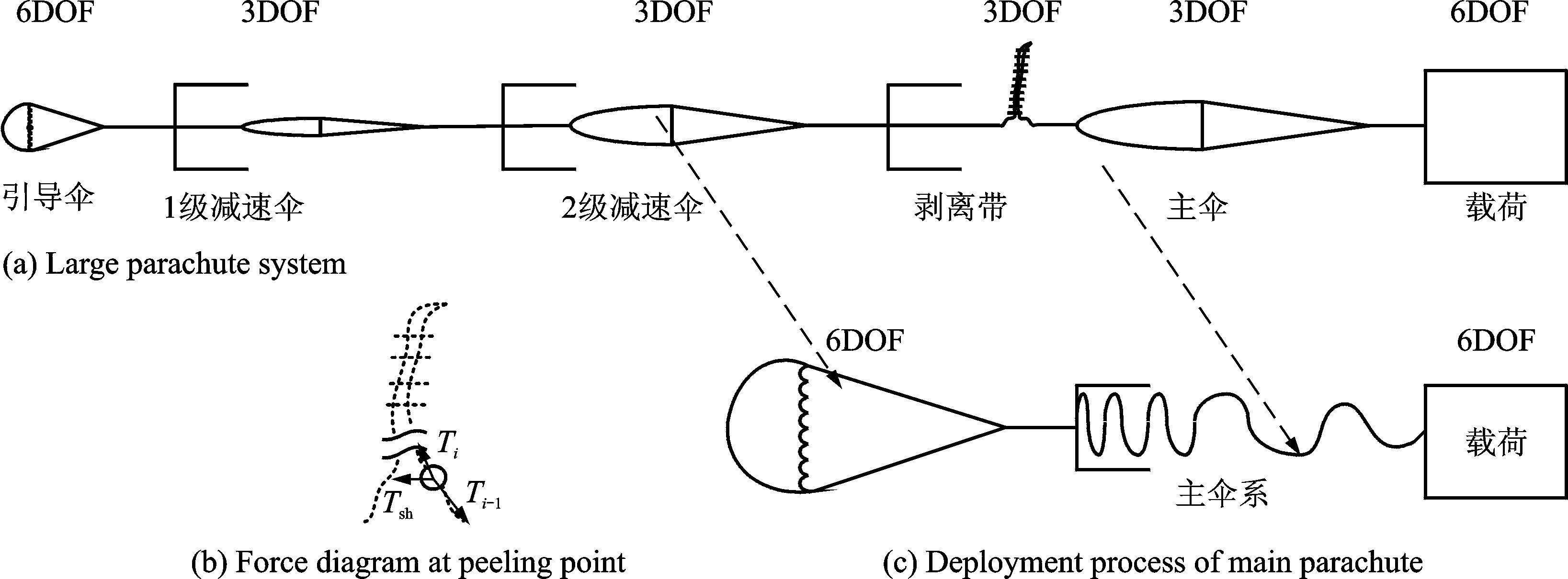
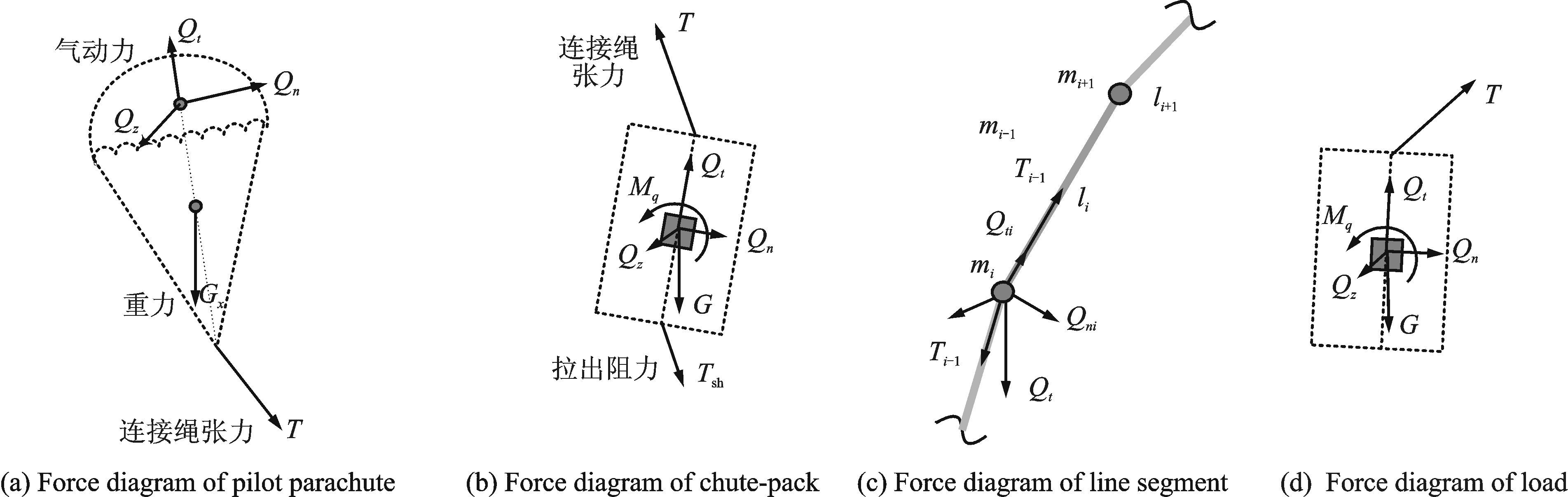
多质点连续拉出模型(以下简称模型B)以绳索动力学理论为基础,将伞绳伞衣吊带等离散为一系列质量节点,各节点在重力(G)、气动力(Q)和邻近质点拉力(T)的影响下运动[14-16]。对于复杂的大型伞系统,常常由串联的多级子伞系统组成,为较好地控制主伞的初始充气外形往往还设计有剥离带连接形式(图 2),具有明显的多阶段控制拉出的特点。为获得载荷、上一级减速伞等姿态变化对降落伞拉出过程的影响,后来有一些学者提出了多质点多刚体非连续拉出模型[1, 17-19](以下简称模型C)。该方法将有可能造成拉伞干扰的其他对象(引导伞、伞包、载荷体等)视为刚体,而拉出降落伞仍然由一系列质点组成,其受力情况如图 3所示。
|
图 2 大型伞系统拉直过程 Figure 2 Deployment process of large parachute |
|
图 3 多体多质点受力示意图 Figure 3 Force diagram of multi-body and multi-particles |
根据对伞-载系统多物体对象的不同处理方式及受力情况,可以得到它们的动力学控制方程及各仿真模型的主要特点,如表 1所示。
| 表 1 不同拉出模型比较 Table 1 Comparisons of different deployment models |
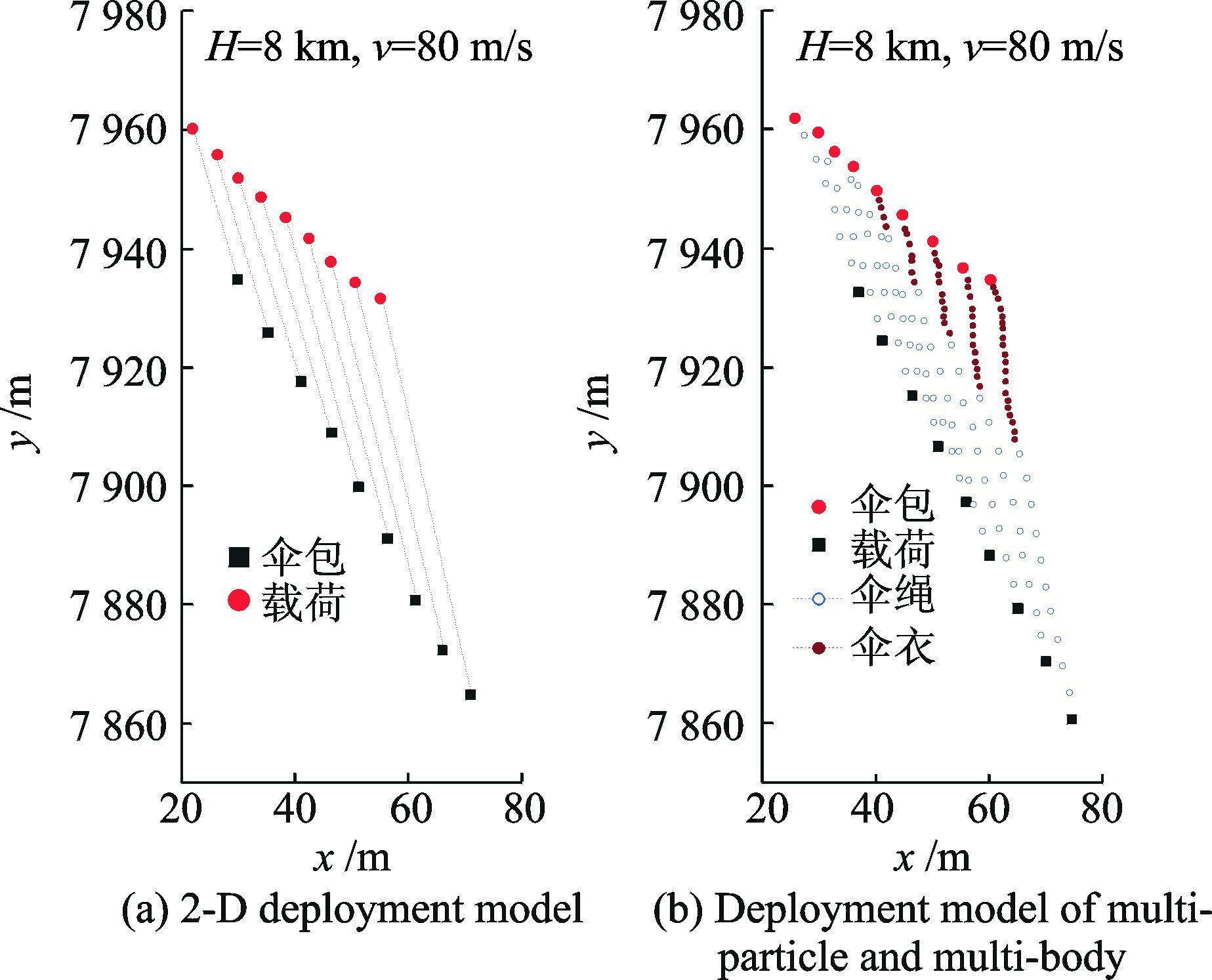
图 4是本文分别采用平面直线拉出模型及多质点多刚体模型得到的神舟飞船主伞系统拉出过程轨迹计算结果;图 5为文献[1]采用多刚体多质点非连续拉出模型仿真得到的拉出过程伞顶甩动情况。可以看出,各模型复杂程度不同,所能实现的仿真效果也不一致。主要有如下特点:
|
图 4 飞船主伞拉直过程轨迹 Figure 4 Deploy trajectory of main parachute of spacecraft |
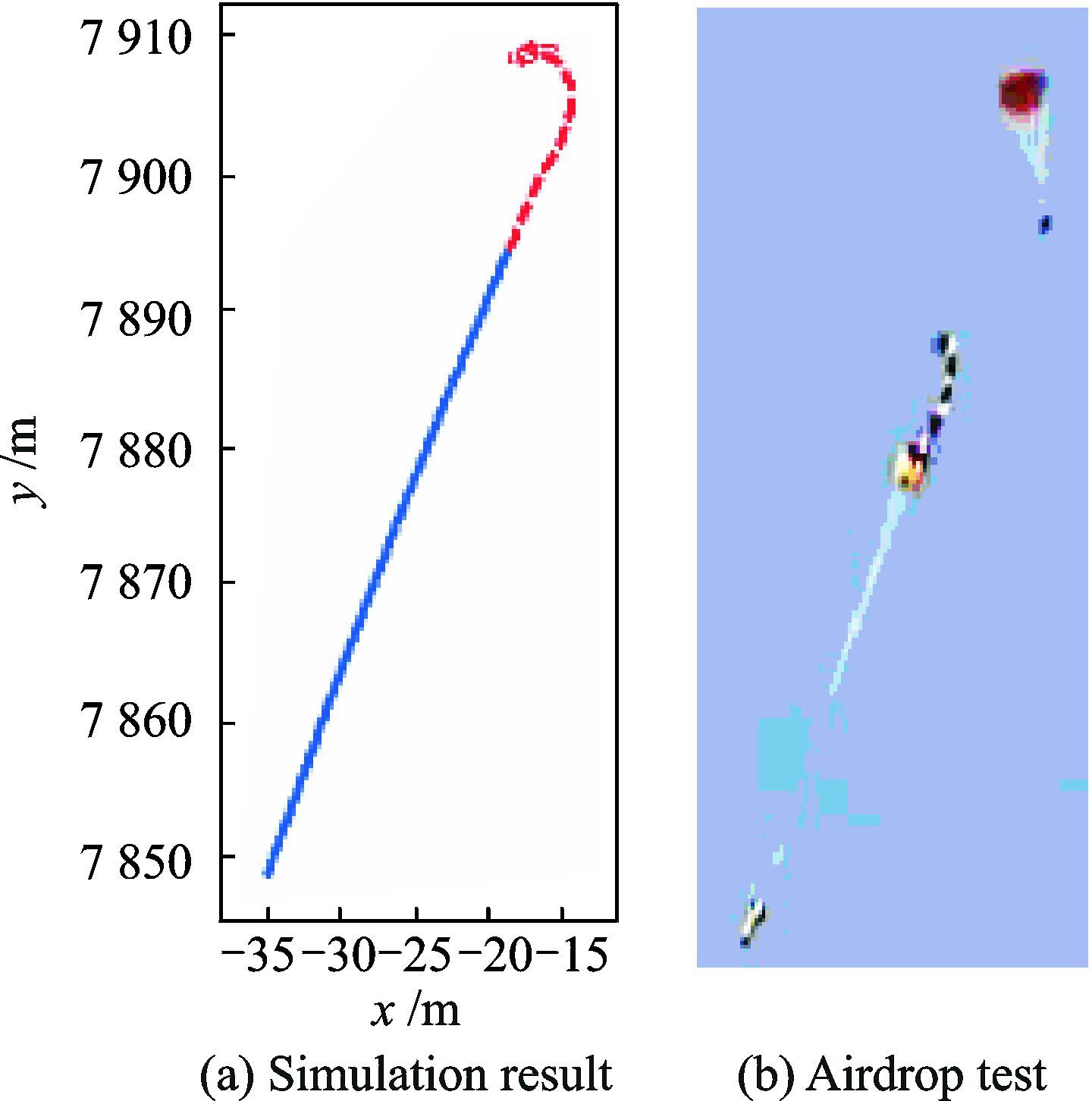
|
图 5 伞顶甩动情况[1] Figure 5 Vent whip of parachute |
(1) 伞系多质点模型可以预测出各微段的速度及轨迹,模拟出拉直过程中的绳帆、弯曲等现象;并能得到各微段的瞬态张力,从而获知伞系统拉直过程中最大张力出现的时刻和位置。
(2) 多刚体多质点模型除可实现模型B的预测效果外,还可获得引导伞(伞包)、载荷体的姿态情况,为拉出过程安全性评估提供更为全面的数据。
(3) 模型越简单,所需要的输入参数越少,编程实现也越简单,但是所得到的信息量也越少。平面直线拉出模型由于方法简单,且可以获得载荷体轨迹及拉直力的动态曲线,工程上应用仍然非常广泛。
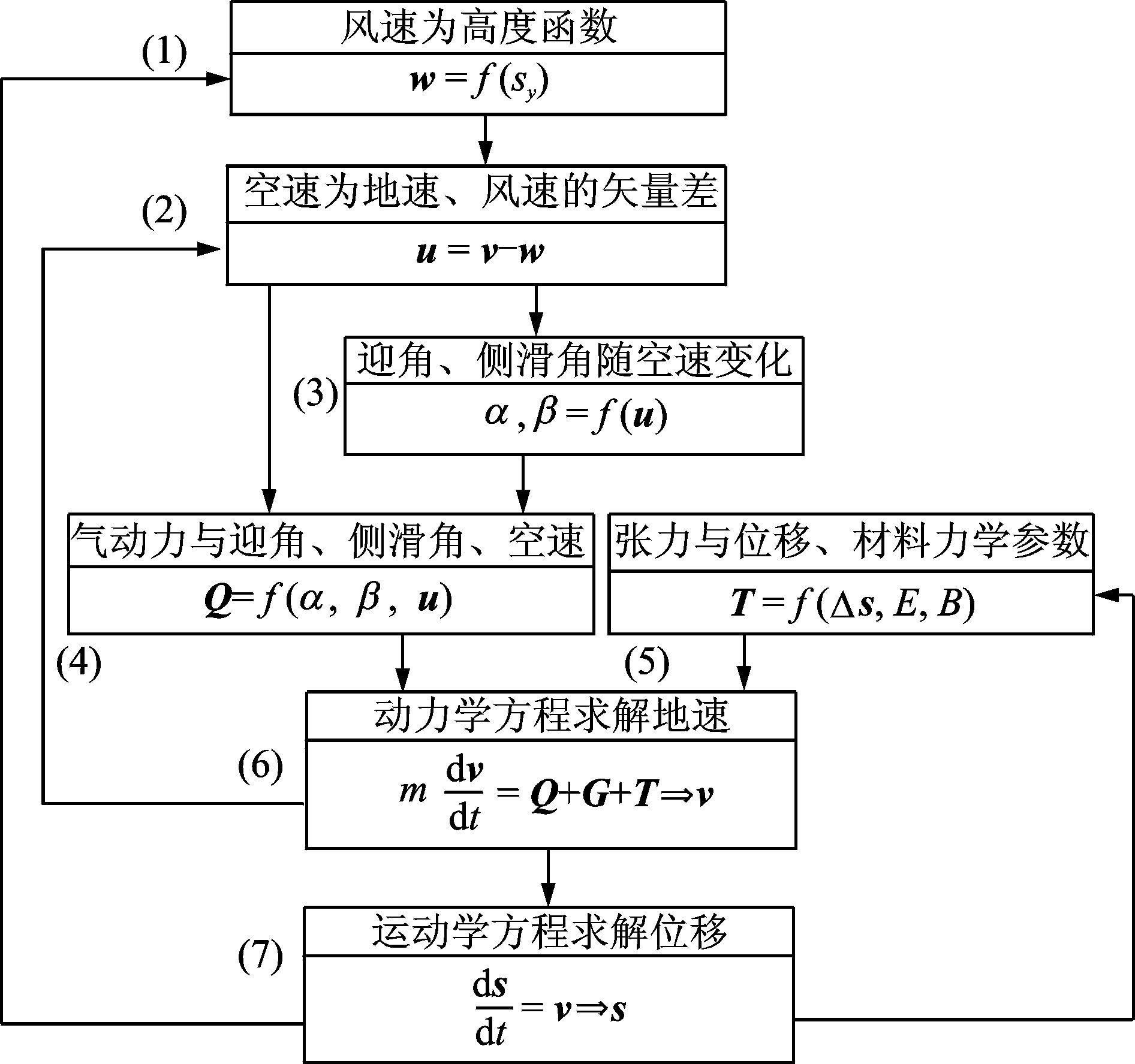
2 作用力建模 2.1 气动力及环境风场拉直过程是多体、多质点、变质量、变自由度动力学问题,虽然各质点(刚体)只受到重力、张力和气动力的作用,但是由于各质点(刚体)的位置、速度、姿态以及环境风场都对气动力、张力计算产生很大的影响,因此动力学模型中的影响因素非常复杂。图 6为拉直过程各因素之间的关系,其中空速与气动力、位移与张力之间的动力学关系在整个拉直过程中起着决定性作用。
|
图 6 动力学模型中主要因素之间的相互关系 Figure 6 Relationship among main factors of dynamic model |
依据绳索动力学理论,各绳段气动力可以采用式(1)计算
| $\left\{ \begin{align} & {{Q}_{ni}}=-\frac{1}{2}{{\rho }_{air}}\left| {{u}_{ni}} \right|{{u}_{ni}}{{C}_{ni}}{{d}_{i}}{{l}_{i}} \\ & {{Q}_{ti}}=-\frac{1}{2}{{\rho }_{air}}\left| {{u}_{ti}} \right|{{u}_{ti}}{{C}_{ti}}{{d}_{i}}{{l}_{i}} \\ & {{Q}_{zi}}=Q{{~}_{ni}} \\ \end{align} \right.$ | (1) |
式中:uni,uti为绳段i体坐标系下的法向、切向空速;Cni,Cti为对应的气动阻力系数,根据Re数及绳段不同的离散程度,气动系数可以采用不同的表达公式[19-20]。
由式(1)及图 2可知,气动力是空速的函数,而动力学方程求解量为地速。由于降落伞质量轻,高空风场对拉直过程的影响比较明显。图 7~8是神舟飞船主伞拉直时间和拉出速度随风速风向的变化情况[19]。从中可以看出,无风速情况下,拉出平均速度为67 m/s,拉直时间为1.27 s。不同的风向条件影响也不尽相同。当风速达到50 m/s时,顺、逆、侧风拉直时间分别为1.48,1.22,1.02 s。风速越大,影响越大;其中侧风影响最强,会加快拉出并造成拉直力增加[19]。

|
图 7 拉直时间随风速偏角的变化 Figure 7 Deploy time at different wind directions |
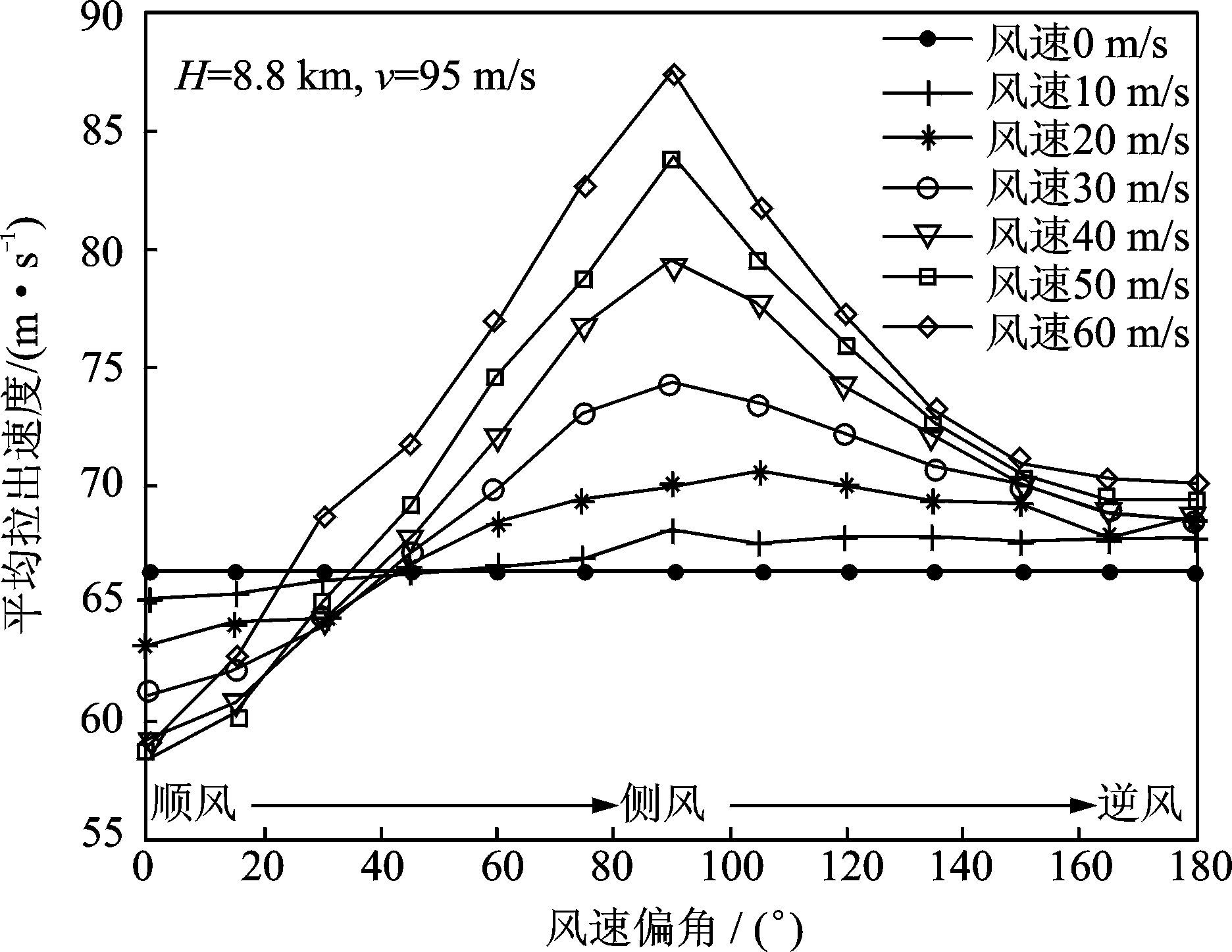
|
图 8 平均拉出速度随风速偏角的变化 Figure 8 Average deploy velocity at different wind directions |
2.2 绳段拉力(拉直力)
柔性绳段只能承受拉力而不能承受压力的作用,拉直过程中每一时刻各绳段的最大拉(张)力称为拉直力。拉直力变化及绳段张力分布一直是拉直过程研究的重点问题,拉直过程研究最早也是始于拉直力的计算[5-7, 17]。绳段拉(张)力理论研究也经历了由简单到复杂的演变过程。主要有两大类研究思想:(1)降落伞的拉力是由于降落伞、载荷体二者之间的相对运动产生,并不考虑织物的弹性,又称为刚性模型[5-6, 18];(2)降落伞织物的拉力是由于材料变形产生,分别有:无质量弹簧模型[18, 21]、一维张力波动模型[22-25]、粘弹性模型[16]及弹簧阻尼模型[1, 9-13]。上述拉力模型的主要特点及数学描述如图 9所示。
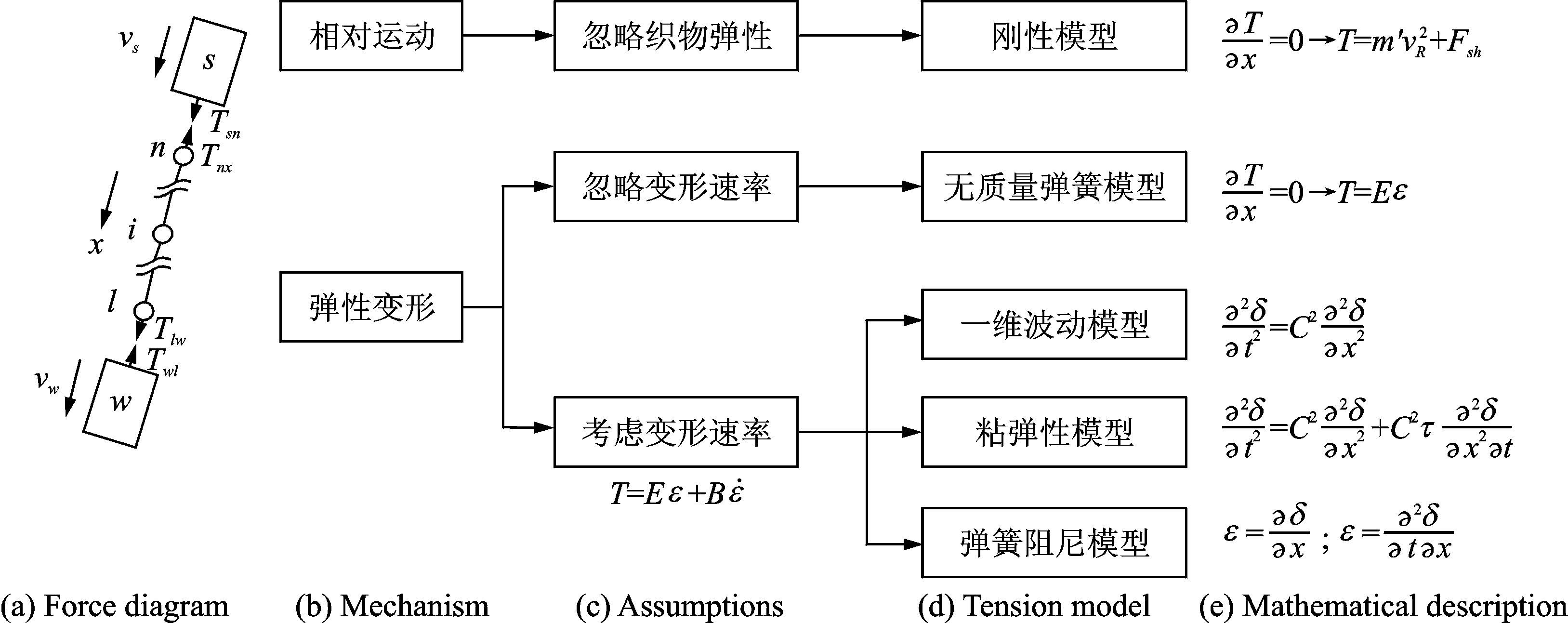
|
图 9 降落伞拉出张力模型 Figure 9 Tension model of parachute deployment process |
本文基于多质点连续拉出方法,分别采用弹簧阻尼模型及无质量弹簧模型对神舟飞船主伞拉出过程进行了模拟。无质量弹簧模型张力波传播速度无穷大,各点张力一致(
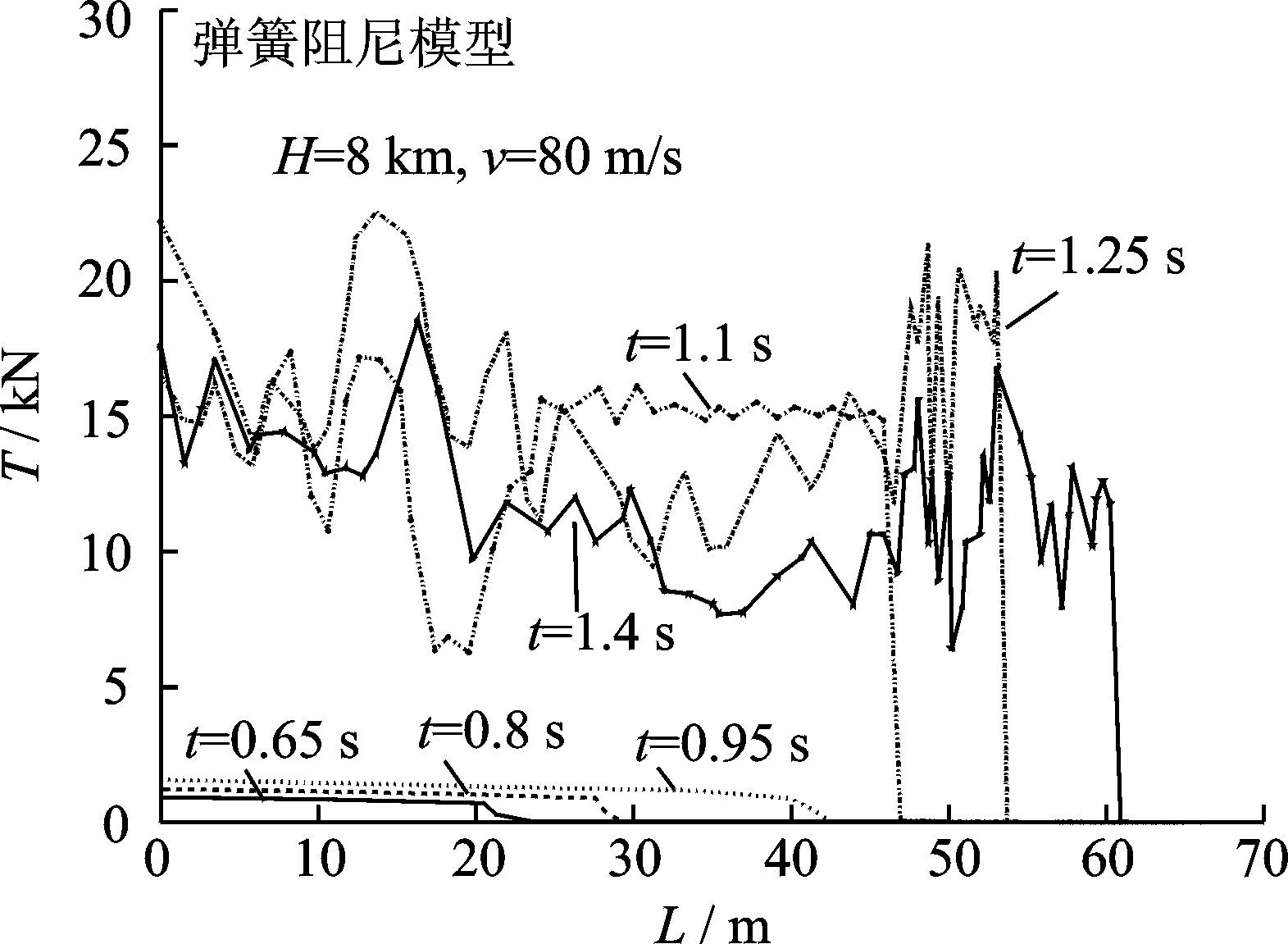
|
图 10 拉出过程张力波的瞬态传递 Figure 10 Tension transient wave of deployment process |
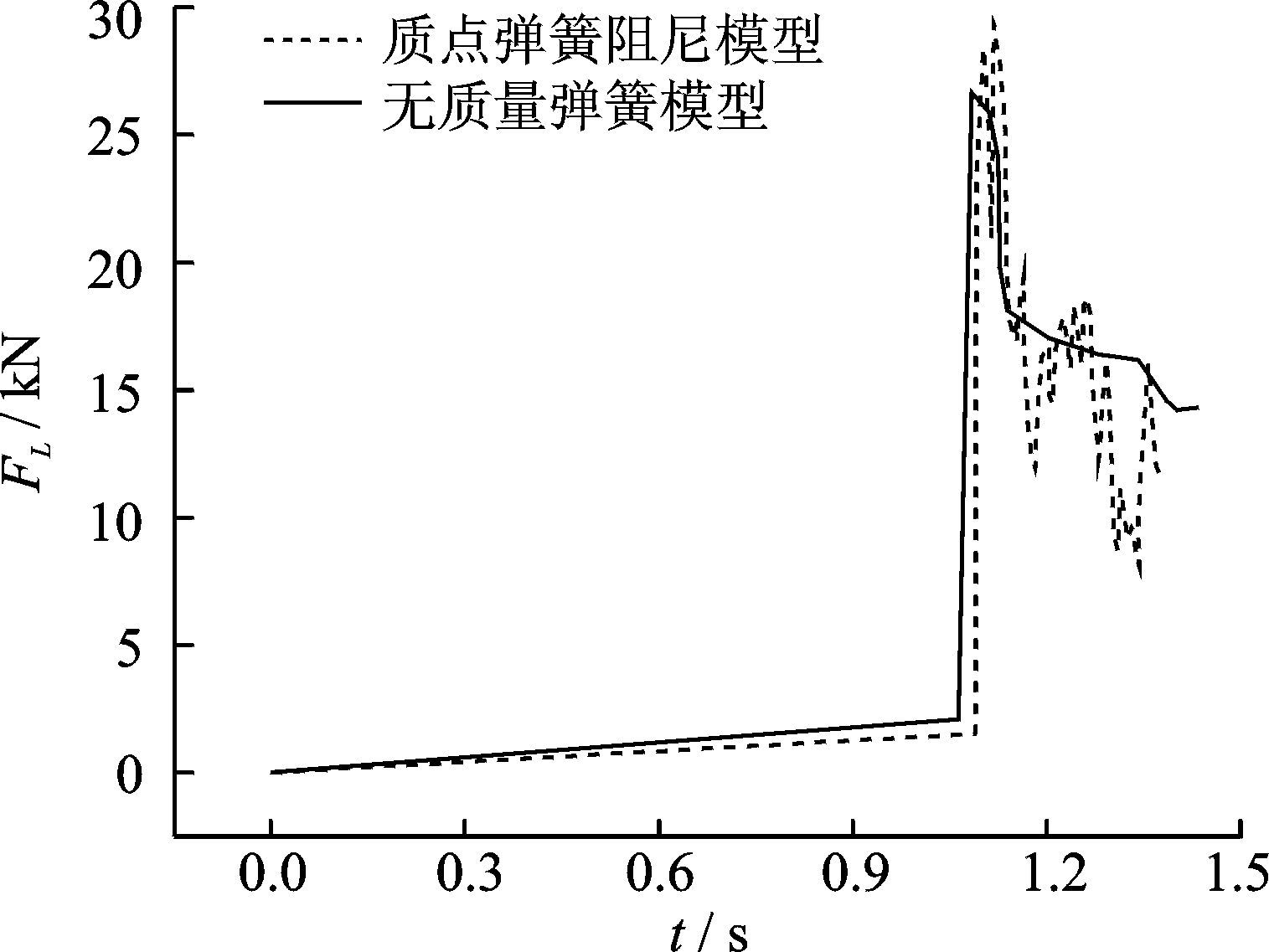
|
图 11 拉直力动态变化 Figure 11 Comparison of snatch load history |
(1) 拉直过程中存在着吸收现象和弥散现象,不同位置不同时刻处的拉力均不相等;考虑织物弹性及变形速度的拉力模型最符合实际情况的物理本质,可应用于平面及三维动力学仿真分析。
(2) 无质量弹簧模型虽然改进了刚性模型织物不变形的假设,但二者均认为每一时刻各点处张力处处相等(
(3) 弹簧阻尼模型相比较于一维波动模型及粘弹性模型,不需要引入波速(C),编程实现上更为容易,在三维计算上有更好的适应性。
(4) 刚性模型简单方便,可用于方案的初步估算;无质量弹簧模型适合于小伞、短伞绳或速度差较小情况下的拉出计算;当需要了解关键点的瞬时状态时则需要考虑变形及变形速率传播的影响。
3 拉直过程仿真技术发展探讨 3.1 准确性无论是实验还是仿真,误差都不可避免。影响降落伞拉直过程仿真性的原因主要有3个方面:(1)伞系统质量分布模型是否准确?(2)是否建立了准确的气动力模型和拉力模型?(3)数值计算时是否采用了合理的时间步长、空间步长及数值算法?
3.1.1 伞系统质量分布拉直过程仿真计算涉及的因素众多,准确的模型可以获得更加精确的仿真结果。质量不仅对运动速度(轨迹)产生很大的影响,对拉力也会产生直接的影响。McVey和Wolf针对锥形带条伞开展了不同质量分配情况下拉出过程动力学仿真的数值试验测试,若采用粗糙的质量分配模型(图 12,质量分配a),计算得到的载荷体加速度(过载)和试验数据相差很大[23-24]。结果表明伞系质量分配对速度、过载都有明显的影响。在仿真分析上,伞-载系统离散单元越多,质量分布越符合真实情况,仿真结果越真实。
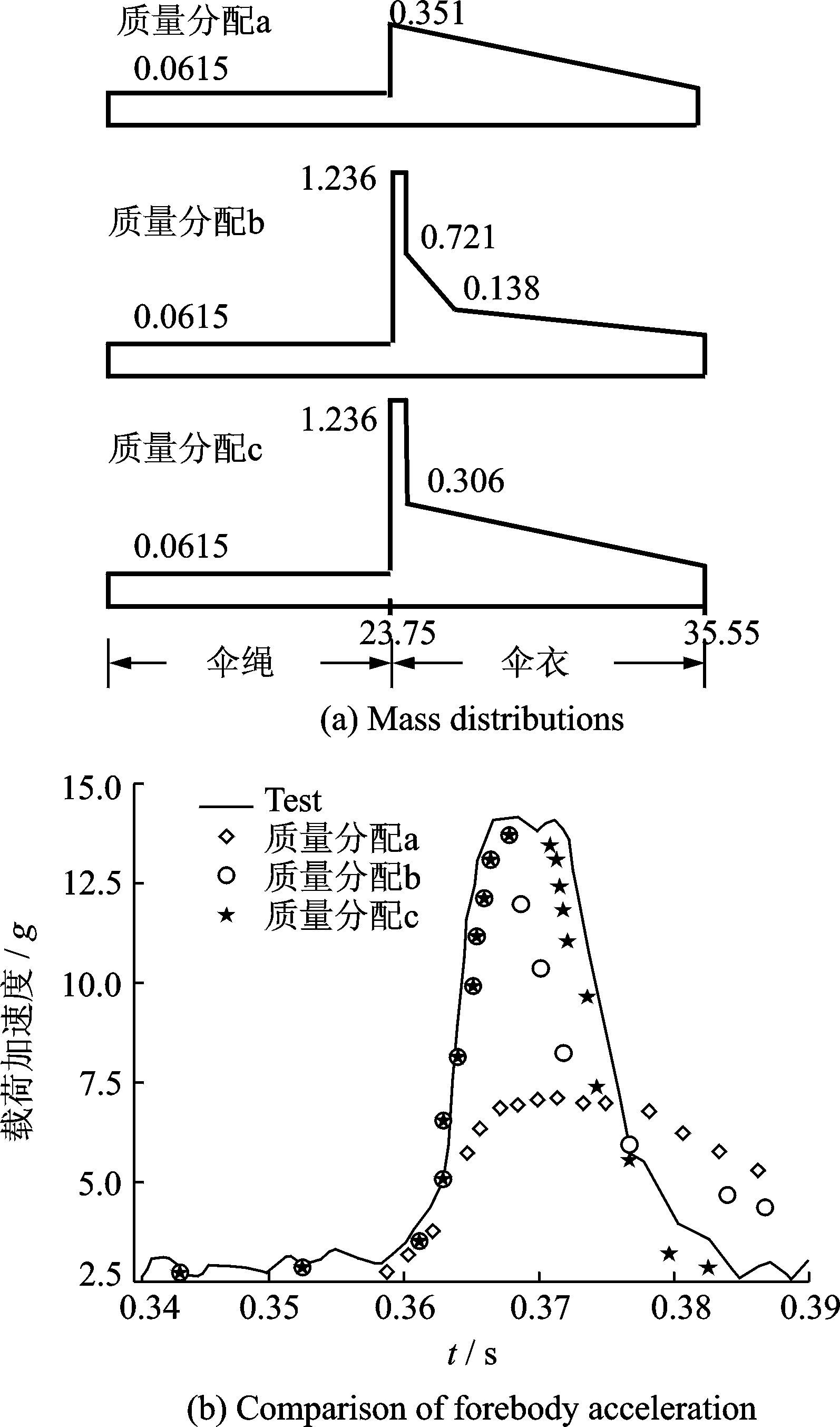
|
图 12 不同质量分配下物体过载比较 Figure 12 Comparison of forebody acceleration in different mass distributions |
3.1.2 作用力模型
拉出过程中的作用力主要有气动力和绳段张力。首先,准确的气动力模型应能适时地反映离散单元外形、气动角度及当地风速的变化,目前在微段单元气动力的计算上对风场模型进行了较大的简化,并忽略了离散单元长度(绳段单元长径比)对气动系数的影响,因而准确的气动力计算模型还有待建立。其次,考虑了织物材料变形及变形速度的拉力模型尽管反应了张力产生的力学本质,但由于织物阻尼系数测量还存在一定困难,材料参数有时需要多次数值试验才能确定;而刚性模型及无质量弹簧模型还存在误差较大的问题,因此更简便准确的拉力模型也有待于进一步发展。
总之,各单元受力虽然简单,但气动力、绳段张力涉及的因素众多,具体计算非常复杂。每一瞬时各研究单元的运动都会引起位置、姿态、速度等的变化,从而对气动力和单元间的内部张力产生很大的影响。一般来说,模型考虑的因素越多,越能反映实际情况,但参数之间的相互影响也越复杂,仿真难度也越大。
3.1.3 求解方法伞-载系统拉出过程是多体、多质点系变自由度问题,而作用力又具有非线性特点,数值求解方法对计算精度有较大的影响,首先要确立合理的时间步长和空间步长。王伟志[25]曾经采用波动方程模型对神舟飞船主伞包拉出过程开展了不同时间步长(10-5~10-6 s)及空间步长(0.01~0.1 m)的计算,发现不同的时-空步长对最大拉力的计算结果并不一致,结果相差约12% ;步长越小,拉力脉动频率越大,若时间步长增加到足够拉出主伞包时,波动方程模型“退化”为无质量弹簧模型。在步长的选取上,采取如下原则:
(1) 无质量弹簧模型和刚性方程模型可以采用较大的时间步长,但一般不大于0.001 s;
(2) 在质量密度变化大的位置(如伞衣、伞衣底边等位置),应进一步减小时间步长和空间步长;
(3) 对于考虑变形及变形传播速度的拉力模型,时间步长常常控制在10-5~10-6 s。
除此以外,数值解法对计算精度也会造成影响,对于降落伞拉出过程,采用四阶Runge-Kutta方法便可达到较高的数值计算精度。
3.2 平台化20世纪初仿真技术就已经开始受到关注,尤其是航空、航天和原子能技术的发展推动了仿真技术的进一步发展。目前,仿真已成为各学科工程领域对系统进行设计、分析、检验必不可少的手段。但是,在降落伞研制领域,仿真技术的发展还相对落后,缺少先进的设计、分析平台供研制单位使用。美国发展得相对比较好,如1989年,Sandia实验室研制了名为“LINESAIL”拉伞过程仿真分析软件[27-28],为F-111救生伞等多个型号研制提供了技术支持。国内国防科技大学、南京航空航天大学等高校也进行了大量的拉伞过程仿真分析工作[1, 11-13, 19, 25],但由于拉伞程序及伞系统结构组成的多样性(单伞、多伞串联、群伞并联等),上述仿真分析工作只针对具体型号,不具备普适性。
由于拉直过程模型的复杂性及拉直程序、降落伞系统组成的多样性,要开发准确及通用性强的拉伞过程仿真软件依然是一项难度比较大的工作。笔者认为应遵循如下思路:(1)模块化设计思想。无论伞系统组成多么复杂不同(图 3),都存在着共同特点:伞系统都是由伞单元组成;拉伞过程只有顺拉、倒拉两种程序。因此可以采用模块化的设计思路进行拉真过程仿真软件的研制开发。(2)抓住本质,弱化细节。通用性是平台研制的基本特点,过份强调细节往往会降低平台的通用性及普适性,建立通用性的仿真数学模型是平台研制的关键。(3)智能化。随着计算机软硬件方面的发展,要求仿真系统能提供建模、运算、数据处理等工程要求,这就要求开展多学科、跨专业的联合仿真,使软件本身具有良好的人机对话环境、智能化的求解器及模型管理,减少软件学习和使用的困难。
3.3 精细化目前降落伞拉出过程的仿真模型主要基于牛顿力学建立,降落伞假设成有限个质点,气动模型建立在试验或经验基础上,通过动力学仿真计算获得开伞初期伞系统各质点的运动情况及开伞拉力。但实际情况是降落伞有很强的柔性,不能抗压,处在前置载荷体及后部伞包(引导伞)干扰流场下,现有方法难以得到精细的非定常空间动态信息。
数值结果的精细化是仿真技术发展的必然要求,为了得到更详尽的结果,从拉直过程的力学机制出发,减少模型的解耦程度和简化程度是其中最重要的两个方面。折叠降落伞拉出过程是在两体运动情况下流场结构相互作用的过程,程涵等采用流固耦合方法对折叠降落伞拉直展开过程进行了模拟[28],是降落伞拉直过程新方法的有益探索。但由于织物折叠建模及流固耦合的复杂性,仅在简化的模型伞上进行了折叠展开过程的仿真,初始折叠状态及伞衣约束情况和真实状态还存在差异。要真正实现降落伞折叠拉直过程的流固耦合计算,还有许多问题解决:如柔性织物折叠(褶皱)网格划分问题[29-30];多层折叠网格畸变及模型误差修正问题[30-31];织物接触及碰撞问题[31-33];大变形流固耦合求解问题[32-34]等。
4 结 论降落伞拉直过程是开伞过程的第一个阶段,在过去的几十年内,降落伞拉直过程动力学建模及仿真技术有了长足的进展,取得了显著的研究成果。主要表现在以下几个方面:
(1) 动力学模型从二维平面扩展到三维空间,从四自由度问题突破至不受自由度限制的多质点多刚体变自由度问题。
(2) 降落伞从忽视织物弹性扩展至考虑了织物的弹性及粘滞性,使拉力及张力波的传播情况更加符合实际。
(3) 仿真数据结果更加丰富:从只能得到两体轨迹扩展至可获得多体轨迹和姿态;从只能得到最大张力动态变化扩展至可以预测出最大载荷出现的时间和位置。
随着计算机软硬件的发展、人们对物理问题的认知加深,降落伞拉直过程仿真技术将会更加准确、精细,成为降落伞工程设计及分析的重要手段。
| [1] |
王海涛.大型降落伞抽打现象及运动稳定性研究[D].长沙:国防科技大学,2011. Wang Haitao. Research on bull whipping and dynamic stability of large parachute system[D]. Changsha: National University of Defense Technology,2011. |
| [2] |
夏刚, 程文科, 秦子增.
航天器回收中几种主伞失效案例介绍[J]. 航天返回与遥感 , 2002, 23 (4) : 4–8.
Xia Gang, Cheng Wenke, Qin Zizeng. Case study of main parachute malfunction in aerospace recovery[J]. Spacecraft Recovery & Remote Sensing , 2002, 23 (4) : 4–8. |
| [3] | Watts G. Space Shuttle solid rocket booster main parachute damage reducing team report [R]. NASA-TM-4437,1993. |
| [4] | French K E. Parachute canopy dimpling collapse mode[R]. Austin, Texas, IAA-84-0796,1984. |
| [5] | Toni R A.Theory on the dynamics of bag strip for a parachute deployment aided by a pilot chute[R].AIAA 68-925,1968. |
| [6] | Toni R A.Theory on the dynamics of a parachute system undergoing its inflation process[R].AIAA 70-1170,1970. |
| [7] | Huckins E K. Techniques for selection and analysis of parachute deployment systems[R]. NASA TN D-5619,1970. |
| [8] | Hckins E K. Snatch force during lines-first deployment of space[J]. J Aircraft , 1971, 8 (3) : 298–299. |
| [9] | Purvis J W. Prediction of parachute line sail during lines-first deployment[J]. J Aircraft , 1983, 20 (11) : 940–945. DOI:10.2514/3.56727 |
| [10] | Eckroth W V,Garrard W L,Miller N.Design of a recovery system for a reentry vehicle[R].AIAA 93-1224,1993. |
| [11] |
张青斌, 程文科, 彭勇, 等.
降落伞拉直过程的多刚体模型[J]. 中国空间科学技术 , 2003, 23 (2) : 45–50.
Zhang Qingbin, Cheng Wenke, Peng Yong, et al. A multi-rigid-body model of parachute deployment[J]. Chinese Space and Technology , 2003, 23 (2) : 45–50. |
| [12] |
张青斌, 彭勇, 程文科, 等.
降落伞拉直过程中的阻尼弹簧模型[J]. 弹道学报 , 2003, 15 (1) : 31–36.
Zhang Qingbin, Peng Yong, Cheng Wenke, et al. A mass spring damper model of parachute deployment[J]. Journal of Ballistics , 2003, 15 (1) : 31–36. |
| [13] |
余莉, 史献林, 袁文明.
牵顶伞在降落伞拉直过程中的作用[J]. 南京航空航天大学学报 , 2009, 41 (2) : 198–201.
Yu Li, Shi Xianlin, Yuan Wenming. Effects of parachute deploymen using attached apex drogue[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2009, 41 (2) : 198–201. |
| [14] | French K E.A first-order theory for the effects of line ties on parachute deployment[R]. AIAA 79-0450. 1979. |
| [15] | Purvis J W.Improved prediction of parachute line sail during lines-first deployment[R]. AIAA 84-0786,1984. |
| [16] |
徐宏, 曹义华, 李栋.
先拉伞绳法数学模型及拉直力预测[J]. 航空动力学报 , 2008, 23 (4) : 706–711.
Xu Hong, Cao Yihua, Li Dong. Mathematical model and snatch force prediction for the lines-first parachute deployment[J]. Journal of Aerospace Power , 2008, 23 (4) : 706–711. |
| [17] |
郭鹏.大型降落伞开伞过程研究[D].长沙:国防科技大学,2012. Guo Peng. Research on the opening process of large parachute system[D]. Changsha: National University of Defense Technology,2012. |
| [18] |
王利荣.
降落伞理论与应用[M]. 北京: 宇航工业出版社, 1997 : 460 -471.
Wang Lirong. Theory and application of parachute[M]. Beijing: Astronautics Publishing House, 1997 : 460 -471. |
| [19] |
史献林. 载人飞船降落伞回收系统拉直过程研究[D].南京:南京航空航天大学,2009. Shi Xianlin. Deployment research on parachute recovery system of manned spacecraft[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2009. |
| [20] | Huston R L, Kamman J W. Representation of fluid force in finite segment cable models[J]. Computer & Structure , 1981, 14 . |
| [21] | Poole L R,HuckinsIII E K.Evaluation of massless-spring modeling of suspension-line elasticity during the parachute unfurling process[R].NASA TN D-6671,1972. |
| [22] | Wbitlock C H,Poole L R.Postflight simulation of parachute deployment dynamics of viking qualification flight tests[R].NASA TN D-7415,1973. |
| [23] | McVey D F, Wolf D F. Analysis of deployment and inflation of large ribbon parachutes[J]. J Aircraft , 1974, 11 (2) : 28–33. |
| [24] | Heinrich E K.A parachute snatch theory incorporation line disengagement implses[R].AIAA73-4641,1973. |
| [25] |
王伟志. 降落伞(回收系统)拉直力计算研究[D].南京:南京航空航天大学,1998. Wang Weizhi. The computing research of parachute snatch load on recovery system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,1998. |
| [26] | Johnson D W. Testing of a new recovery parachute system for the F-111 aircraft crew escape module: An update[R].DE89-007139,1989. |
| [27] | Maydew R C, Peterson C W , Orlik-Rueckemann K J. Design and testing of high-performance parachutes[R]. AD-A246343, 1991. |
| [28] |
程涵, 余莉, 李少腾, 等.
折叠降落伞展开过程研究[J]. 航天返回与遥感 , 2012, 33 (2) : 1–6.
Cheng Han, Yu Li, Li Shaoteng, et al. A study on the opening process of folded parachute[J]. Spacecraft Recovery & Remote Sensing , 2012, 33 (2) : 1–6. |
| [29] |
白远利, 张金换, 黄世霖.
一种映射算法在IMM法气袋建模中的应用[J]. 清华大学学报 , 2002, 42 (11) : 1528–1531.
Bai Yuanli, Zhang Jinhuan, Huang Shilin. Mapping algorithm for airbag modeling with the initial metric method[J]. Journal of Tsinghua University: Science and Technology , 2002, 42 (11) : 1528–1531. |
| [30] |
程涵, 余莉, 张鑫华, 等.
基于IMM 修正的降落伞折叠建模方法[J]. 计算机辅助设计与图形学学报 , 2013, 25 (5) : 751–757.
Cheng Han, Yu Li, Zhang Xinhua, et al. Folded parachute modeling method based on IMM[J]. Journal of Computer-Aided Design & Computer Graphics , 2013, 25 (5) : 751–757. |
| [31] | Zhan Yanan, Yu Li, Yang Xue, et al. Initial stress correction method for the modeling of folded space inflatable structures[J]. Aviation , 2014 . |
| [32] | Xu Zhenlong. Parallel finite element methods for modeling contact in geometrically nonlinear membrane structures[D]. Connecticut:University of Connecticut,2002. |
| [33] | Stein K R. Simulation and modeling techniques for parachute fluid-structure interactions[D]. Minnesota:Doctoral thesis of the University of Minnesota, 1999. |
| [34] | Takizawa Kenji, Tezduyar Tayfun E. Computational methods for parachute fluid-structure interactions[J]. Arch Comput Methods Eng , 2012, 19 : 125–169. DOI:10.1007/s11831-012-9070-4 |
 2016, Vol. 48
2016, Vol. 48


