2. 陆军航空兵学院航空机械工程系,北京,101116 ;
3. 试验物理与计算数学国家级重点实验室,北京,100076
2. Department of Aeronautical Engineering, Army Aviation Institute, Beijing, 101116, China ;
3. National Key Laboratory of Science and Technology on Test Physics & Numerical Mathematics, Beijing, 100076, China
在超声速飞机总体设计阶段,方案外形设计往往聚焦于机翼外形参数的优化设计[1-5]。而在气动布局和机翼主要参数确定的情况下,减小阻力尤其是激波阻力是超声速飞机外形设计的主要工作之一[6]。
基于面积律理论合理安排机身、机翼等部件的组合形式并对飞机方案外形进行精细化修整是减小阻力的主要途径[7]。在飞机概念设计过程中,对机身的剖面设计一般从特定的目标出发,如提高侧向隐身性能[8],或保证前后机身部件连接曲面的光顺性[9]等方面。而各种基于面积律概念的超声速减阻设计方法研究[10-13]始终是超声速飞机设计研究中的一个重要方向。将飞机剖面设计与基于面积律的减阻方法结合起来,是提高超声速飞机概念方案设计效率的有效途径之一。
本文针对超声速飞机概念设计阶段外形快速调整问题,提出了基于面积律自动判别的飞机概念设计方案机身几何外形调整方法,通过对飞机概念方案的截面积分布曲线进行分析,建立了针对不同截面积曲线类型的外形调整方法,通过曲线的光顺性特征分析探寻飞机横截面积不合理的站位,并通过分析给出对应的量化外形调整建议,从而可辅助设计人员快速定位需修形位置,并辅助实现基于面积律的飞机机身几何外形调整。最后通过飞机概念设计方案机身几何外形调整实例中的应用对本文方法进行了验证。
1 截面积分布曲线光顺性分析根据线化的面积律理论,飞机激波阻力随体积沿纵轴方向分布曲线的曲率有关,减小激波阻力的途径包括减小飞机的最大横截面面积和减小截面积分布曲线的曲率。根据面积律分布曲线的光顺情况分析结果对飞机外形进行修形是面积律曲线重要作用之一,通常方法是由设计师通过观察曲线曲率的变化来判断需要修形的位置,既需要设计师去分析判断曲线哪些位置存在不光顺的情况,还要对这些位置的剖面外形进行反复的修形调整。这种方式效率低,需要对所需修形位置逐一判断并调整剖面外形,修形的效果也无法及时得到反馈。而通过软件自动对面积律曲线进行判断,找到曲线上不光顺的位置并给出所对应的飞机站位,进一步可以建议相应的飞机剖面面积调整大小,则可以极大地提高设计师的工作效率,即设计师只需要根据建议的站位和修形建议进行对应的剖面调整,工作重点完全放在飞机剖面外形设计上来。根据面积律曲线通过程序自动判别需要修形的位置,主要工作在飞机快速概念设计软件SEACD[14]中进行。
基于面积律理论的飞机截面积分布曲线分析方法可按以下步骤进行:
(1) 分析截面积分布曲线中截面积阶跃的情况,即在某个站位上的截面积较上一个相邻站位发生了较大的增加或减小,改变量导致面积分布曲线出现了一个台阶形状,此时意味着截面积分布是不连续和不光滑的,在这种位置将产生较大波阻,需要对此进行外形修形;
(2) 分析截面积分布曲线的峰值点和极值点,根据面积律原理对曲线峰值点位置进行判断,并对降低截面积最大值给出建议。而对存在波动的曲线情况,曲线存在不止一个极值点,根据“削峰填谷”原则给出对曲线进行光顺的建议,相应地给出在外形修形中需要进行增减的剖面面积建议值,辅助进行外形修形;
(3) 分析截面积分布曲线上存在的“拐点”、曲率剧烈变化的尖角点等曲线不光顺情况,即从使截面积分布曲线尽量光滑以减小波阻的方面考虑,尽量减小面积分布曲线的曲率变化较大的位置。
下面分别介绍截面积分布曲线分析方法。
1.1 截面积阶跃判断方法设截面积曲线上数据点均匀分布,则相邻数据点之间的y向距离(即纵坐标的差的绝对值)可以体现截面积数据的变化大小。设数据点个数为n,第i个数据点与第i- 1个数据点的y向距离表示为
| $\Delta {{y}_{i}}=|{{y}_{i}}-{{y}_{i-1}}|$ | (1) |
则所有相邻数据点y向距离的平均值为
| $\Delta =\text{ }\sum\limits_{i=1}^{n}{\Delta {{y}_{i}}/n}$ | (2) |
以平均值为依据设置判断条件:当两个相邻
数据点y向距离大于2倍的平均值时判定该处存在阶跃,即
| $\Delta {{y}_{i}}>2\Delta y$ | (3) |
记录计算Δyi的两个点的站位值,作为指示需要修形位置的参考。
1.2 离散曲线极值识别法截面积分布曲线的峰值点对应着飞机最大截面积,其判断方法即为给定一组数据寻找最大值,本文不再赘述。而极值点对应了截面积的局部特征,是飞机外形修形应主要关注的情形之一,需要对其进行分析识别和记录。极值点是在一组数据点范围内进行判断的,其存在性受到数据数量影响。数据点范围过大可能导致极值点被边界处较大数据值所掩盖,范围过小则增加分析计算量。因此,需要选取合适的数据范围进行极值点分析。
判断极值的最小数据区间是3个点,由于取点区间的边界不作为极值分析点,所以3点区间只能分析中间点是否为极值。本文中为确保对所有数据点进行极值判别同时不产生重复判别结果,采取如下方法:以最小数据区间为基本单元,从曲线起始点开始对基本单元内的数据点进行判断分析,然后将下一搜索区间的起点设为上一区间的极值分析点,则上一搜索区间的后边界点可以在新的数据区间进行极值判别,这样可以提高搜索速度,并且已经进行极值判别的点不会被重复判别。
以极大值为例,上述极值的判断方法如下:
设起始站位为xj,搜索区间数据点的数量为m,则极值搜索区间为[xj, xj+m-1]。找到该区间中的最值ymaxk=max(yi, j≤i≤j+m-1) ,当极值点不位于边界时,即ymaxk>yj且ymaxk>yj+m时,则点ymaxk识别为极大值点,k为记录的极值点序号。而下一搜索区间为[xj+m-2, xj+m+1],重复上述过程进行极值分析,如此迭代直至曲线数据结束。采集到的极值点数据独立记录,可为后续基于极值点的辅助修形提供基础。
1.3 离散曲线拐点识别法拐点是指由离散点依次连接所构成的曲线上表征曲线曲率方向改变的特征点,拐点两侧曲线的凹凸方向是相反的,因此可以用拐点来标识曲线的凹凸变化。这里采用的是一种基于相邻四点叉积的拐点判断法[15]。
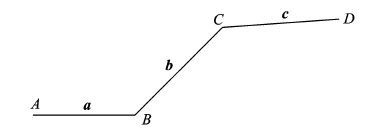
方法基本原理是两个不共线矢量的叉积可决定所成转角的凸凹特征即拐点是否存在的条件。故对于拐点存在区间的判别,可通过对每相邻4点(A, B , C, D)(其中每相邻3点不共线)进行分析来实现。如图 1所示,A,D点是否位于B,C点连线的异侧,可确定这4点内是否存在拐点,从而确定拐点区间。由这4个有序点可形成3个有序矢量(a,b,c),这3个有序矢量可形成两个有序的矢量叉积。拐点存在的充要条件就是曲线凹向改变,即
| $\left( a\times b \right)\cdot \left( b\times c \right) <0$ | (4) |
此时拐点位于B,C点之间,为便于分析和描述,这里称B,C点为临近拐点。当某点连续成为临近拐点时,该点处则构成一个尖角。
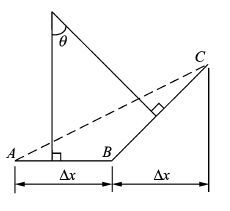
1.4 基于近似曲率的曲线光顺分析法飞机截面积分布曲线通常是由一系列轴向距离相等的离散点连接构成的多段曲线,每一点处的精确曲率获取较为麻烦。而曲率及曲率的变化可以反映曲线的凹凸变化,是对曲线进行光顺分析的重要依据。基于离散点均匀分布的特点,本文引入近似曲率以描述不同离散数据点处曲线形状变化。如图 2所示,B点的近似曲率可以由两相邻线段法线的相对转角变化率获得
| $\rho =\theta /\Delta x$ | (5) |
|
图 2 近似曲率计算示意图 Figure 2 Schematic of calculation of approximate curvature |
式中:θ为相邻线段对应法线的转角,由A,B,C三点构成三角形的∠ABC计算得到;Δx为数据点的站位间距。
根据计算得到每一站位处的近似曲率,即可对截面积分布曲线进行光顺性分析,近似曲率剧烈变化的站位,即对应了截面积分布异常变化的位置。结合拐点分析结果,即可对截面积曲线上的尖角、凹凸变化进行判别。
2 基于面积律的机身外形辅助修形通过曲线分析,可以获取曲线上存在的阶跃、峰值点、极值点、拐点和尖角等信息,这些信息描述了截面积分布曲线的不光顺程度,可以作为飞机机身几何外形修形的依据。采用计算机程序对具体站位处的截面积信息进行分类判断,再结合所在站位的飞机部件信息分析,可给出对应的修形建议。
根据面积律原理进行飞机机身几何外形修形的主要原则有两点:一是尽量保证截面积分布曲线平滑光顺,减少体积突变的情况;二是尽量在保持曲线光顺的前提下减小最大截面积,即降低曲线的最大值,这是降低飞机激波阻力的最直接的方法。从这两点修形原则出发,提出飞机方案机身几何外形辅助修形方法。
2.1 基于曲线最值和极值的修形找到曲线的最大值,定位该站位处的部件信息,并判断该站位位置是否合理。根据希尔斯哈克体标准外形[16],最大值位置应位于飞机的中部附近,如果过于靠前或靠后都将对波阻有增大的影响。本文中根据经验对合理最大值所在区间定义为40%~70%机身长,超过该范围即会发出提示,建议调整部件位置和截面积以使符合面积律。
若站位xi存在极值且整条曲线不止一个极值存在,则给出该站位处各部件信息,并重点提示截面积较大的部件,可通过减小(对应极大值)/增大(对应极小值) 截面积和移动该部件对截面积曲线进行光顺处理。本文中主要探讨第一种处理方式。
2.2 基于截面积曲线光顺性的修形若站位xi存在阶跃情况,且经过判断yi和yi+1的相对大小后得到截面积增大(或减小)的信息,则该站位处外形有两种处理方式:一是该站位之后的外形需要减小截面积;二是将该站位处的某些部件进行沿机体轴的前后移动,以确保截面积不会瞬间增大,从而保证截面积曲线光顺。
对于曲线上拐点和尖角等信息的处理较为复杂一些,需要配合相邻的极值点组成“峰值站位区间”或者“谷值站位区间”,再根据这些区间给予外形调整的建议。对于局部只有凹曲线而不存在“谷值区间”的情况,可由凹曲线两端的拐点构成“凹曲线站位区间”。对站位区间的处理具体如下:以极值点和尖角点为依据,配合其临近拐点,构成对应的“峰值”、“谷值”/“凹曲线”站位区间。从第一个极值点开始,与其相邻的拐点组成第一个“峰值站位区间”,而下一个极小值点附近的拐点和该极值点构成了第一个“谷值站位区间”,或者由两个位于凹曲线两端的拐点与尖角点构成“凹曲线站位区间”,依次类推,可以获得n个站位区间。修形的规则即是尽量将“谷值站位区间”或“凹曲线站位区间”填满,而将“峰值站位区间”的极值减小。
以两“峰值”夹一“谷值”站位区间的典型曲线形状为例,分析对截面积分布曲线修形方法。
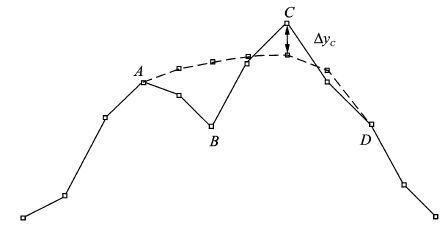
在此情况下,曲线需要进行“削峰填谷”才能满足面积律要求。如图 3所示,极大值点A(xA, yA)、C(xC, yC)与临近拐点构成了两个“峰值站位区间”,而极小值点B(xB, yB)和拐点构成了这两个区间中的“谷值站位区间”,对该种类型的修形方法采取减小较大峰值C区间的截面积,增大谷值区间的截面积的方法,具体如下:
值较小的A峰值区间保持不变,减小极大值C,再根据A和新C点的值对其余点进行插值,从而生成新的截面积参考曲线,如图 3中虚线所示。本文中采取线性插值方法获取。具体公式如下
| $y{{\prime }_{C}}={{y}_{C}}-\Delta {{y}_{C}}$ | (6) |
| $\Delta {{y}_{C}}=12({{y}_{C}}-{{y}_{A}})$ | (7) |
| $y{{\prime }_{B}}={{y}_{A}}+(y{{\prime }_{C}}-{{y}_{A}})m/n$ | (8) |
|
图 3 典型飞机截面积曲线修形示意图 Figure 3 Modification on typical section area curves |
式中:y′C为极大值站位点C调整后的数值;yA, yC分别为极大值站位点A, C原数值;y′B为极小值站位点B经过插值调整后的数值;m为B点与A点间点数量;n为C点与A点间点数量。
对于“谷值”区间退化为包含“尖角”的“凹曲线”区间的情况,以曲率最大的尖角点B为基础,向前、后分别搜索拐点或近似曲率接近0的点A, C,利用式(8) 对A, C之间的点进行插值计算,得到修形建议值。
3 飞机概念方案机身外形修形实例对一种设想的远程轰炸机方案(Long range bomber, LRB)进行基于面积律辅助分析的机身几何外形修形。该方案为了取得远航程和高巡航速度,采取双后掠超声速“箭”形翼布局,经过机翼优化后的方案外形如图 4所示。为了进一步降低该方案的阻力,需要对其剖面外形进行较为细致的修形。而该方案外形较为简单,只有机翼、座舱、机身及双垂尾等部件,因此修形主要表现在对机身和座舱剖面的修剪以及尾翼的位置调整上。

|
图 4 超声速远程轰炸机LRB方案 Figure 4 Configuration of supersonic LRB |
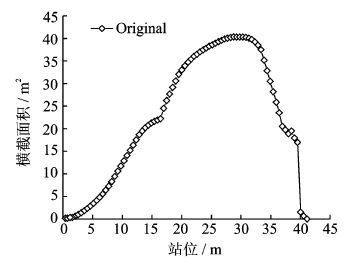
通过截面积计算得到LRB方案的截面积分布曲线,如图 5所示。可以看到,曲线存在着不光顺的情况且最大截面积达到了40.342m2。利用本文提出的快速曲线分析方法,得到了截面积曲线的分析结果,限于篇幅,选取部分典型结果列入表 1。表中列出了自动分析得到的拐点、极值点、最大值点、尖角点及阶跃点等多个典型不光顺和特殊位置,并给出了对应站位处的部件分布情况。
|
图 5 远程轰炸机方案LRB的初始截面积分布曲线图 Figure 5 Original section area distribution curves of LRB |
| 表 1 LRB截面积分布曲线部分典型分析结果 Table 1 Typical analysis results of section area distribution curve of LRB |
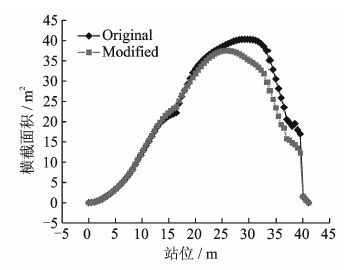
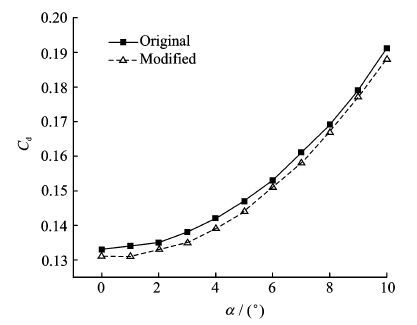
利用本文提出的基于面积律的方案外形辅助修形方法,在截面积分析的基础上,针对性地提出了基于曲线光顺的修形建议,选取典型建议和手动修形后的结果列于表 2。可以看到,在修形建议的基础上,对尖角点附近凹曲线区间和最大值等特殊位置的修形都取得了良好效果,近似曲率都得到了不同程度的下降。修形前后截面积分布曲线对比见图 6,修形后的LRB方案外形见图 7。根据修形建议,对前后机身连接处的机身剖面形状进行了适当增大调整,减小了截面积分布曲线在此处的近似曲率。对最大截面积站位附近进行了“削峰”修形,适当减小了机身剖面面积,同时对后机身尾部进行了收缩修形,降低了截面积曲线在此处的阶跃情况。未修形时,截面积最大位置位于28.74 m站位处,约70%机身长,而修形后的截面积最大位置位于25.66 m站位处,约62%机身长。最大截面积由40.342 m2下降为37.54 m2。采用基于欧拉方程的MGAero气动计算软件计算了修形前后LRB方案在Ma为1.2时的阻力系数,对比曲线见图 8。可以看到,经过修形后,阻力系数减小了约1.5%。结果证明了本文提出修形方法的有效性。
| 表 2 LRB部分修形建议与修形后结果 Table 2 Results and recommendations of adjustment on LRB |
|
图 6 LRB修形前后截面积分布曲线对比 Figure 6 Comparison of section area curves of original and modified LRB |

|
图 7 LRB修形后外形图 Figure 7 Configuration of modified LRB |
|
图 8 LRB修形前后阻力系数对比 Figure 8 Comparison of drag coefficient of original and modified LRB |
4 结论
本文在飞机截面积曲线光顺性综合分析的基础上,提出了一种基于面积律原理的飞机方案机身几何外形计算机辅助快速修形方法,经实例验证表明:
(1) 方法可实现飞机截面积曲线快速辅助分析,对曲线中存在的极值点、拐点、尖角点及阶跃点等信息实现实时分析与结果显示;
(2) 方法依据面积律原理对截面积曲线调整所形成的建议可以有效指导飞机方案的机身几何外形修形工作,对需要调整的剖面位置准确定位并提供剖面面积调整数值建议;
(3) 对最大截面积大小及位置的调整,配合截面积曲线光顺性修形,能够在不改变飞机方案布局形式的前提下有效降低激波阻力,实例中修形后飞机阻力系数下降了1.5%,证明了辅助修形方法的有效性。
| [1] |
胡添元, 余雄庆.
多学科设计优化在非常规布局飞机总体设计 中的应用[J]. 航空学报 , 2011, 32 (1) : 117–127.
Hu Tianyuan, Yu Xiongqing. Preliminary design of unc onventional configuration aircraft using multidisciplinary design optimization[J]. Acta Aeronautica et Astronautica Sinica , 2011, 32 (1) : 117–127. |
| [2] |
白振东, 刘虎, 徐敏, 等.
飞机总体设计优化中的多目标方案优选方法[J]. 航空 学报 , 2009, 30 (8) : 1447–1453.
Bai Zhendong, Liu Hu, Xu Min, et al. Preferred selection method for multiobjective concepts in aircraft conceptual design optimization[J]. Ac ta Aeronautica et Astronautica Sinica , 2009, 30 (8) : 1447–1453. |
| [3] | Choi S, A lonso J J, Kroo I M, et al. Multi-fidelity design optimization of low-boom sup ersonic business jets[R]. AIAA-2004-4371, 2004. |
| [4] |
冯晓强, 李占科, 宋笔锋.
超声速客机低音爆布局反设计技术研究[J]. 航空学报 , 2011, 32 (11) : 1980–1986.
Feng Xiaoqiang, Li Zhanke, Song Bifeng. A research on inverse desi gn method o f a lower sonic boom supersonic aircraft configuration[J]. Acta Aeronautica et Astronautica Sinica , 2011, 32 (11) : 1980–1986. |
| [5] |
朱自强, 王晓璐, 吴宗成, 等.
支 撑机翼跨声速民机的多学科优化设计[J]. 航空学报 , 2009, 30 (1) : 1–11.
Zhu Ziqiang, W ang Xiaolu, Wu Zongcheng, et al. Multi-disciplinary optimization of strut-brac ed wi ng transonic transport[J]. Acta Aeronautica et Astronautica Sinica , 2009, 30 (1) : 1–11. |
| [6] | Nikolic V, Jumper E J. Zero-lift wave drag calculation using super sonic area rule and its modifications[R]. AIAA-2004-217, 2004. |
| [7] |
关晓辉, 宋笔锋, 李占科.
超声速翼身组合体激波阻力优化的EFCE算法[J]. 航空 学报 , 2013, 34 (5) : 1036–1045.
Guan Xiaohui, Song Bifeng, Li Zhanke. Extended far-field com posite element supersonic wing-body wave drag optimization method[J]. Acta A eronautica et Astronautica Sinica , 2013, 34 (5) : 1036–1045. |
| [8] |
白振东, 刘虎, 武哲.
低 可探测机身参数化造型与优化[J]. 北京航空航天大学学报 , 2007, 33 (12) : 1391–1394.
Ba i Zhendong, Liu Hu, Wu Zhe. Parametric modeling and optimization of low observab ility fuselage in aircraft conceptual design[J]. Journal o f Beijing Universit y of Aeronautics and Astronautics , 2007, 33 (12) : 1391–1394. |
| [9] |
卢新来, 刘虎, 王钢林, 等.
基于多Agent的机身外形优化模型[J]. 南京航空航天大学学报 , 2007, 39 (3) : 312–316.
Lu Xinlai, Liu Hu, Wang Ganglin, et al. Fuselage shape optimizatio n model b ased on multi-agent[J]. Journal of Nanjing University of Aeronautics & Astr onautics , 2007, 39 (3) : 312–316. |
| [10] | Palacios F, Alonso J J, Colonno M, et al. A djoint-based method for supersonic aircraft design using equivalent area distri butions[R]. AIAA-2012-0269, 2012. |
| [11] | Forbes A H, Patel A, Komerath N. Drag prediction for supersonic hydrogen-fueled airliners[R]. AIAA-2011-3968, 2011. |
| [12] | Lovell D A. European research to redu ce drag for supersonic transport aircraft[R].AIAA-99-3100, 1999. |
| [13] |
陈真利, 张彬乾, 孙静.
基于面积律概念的超音速减阻设计方法[J]. 西北工业大学学报 , 2006, 24 (4) : 523–527.
Chen Zhenli, Zhang Binqian, Sun Jing. A more efficient desig n method for supersonic drag reduction[J]. Journal of Northwestern Polytechnic al University , 2006, 24 (4) : 523–527. |
| [14] | Liu H, Wu Z, Wang G L, et al. Impleme ntation of a Sketch Based Approach to Conceptual Aircraft Design Synthesis and M odeling[J]. Chinese Journal Of Aeronautics , 2004, 17 (4) : 207–214. DOI:10.1016/S1000-9361(11)60238-0 |
| [15] |
毋河海.
数字曲线拐点的自动确定[J]. 武汉大学学报信息科学版 , 2003, 28 (3) : 330–335.
Wu Heha i. Automatic determination of inflection point and its application[J]. Geomati cs and Information Science of Wuhan University , 2003, 28 (3) : 330–335. |
| [16] |
王 晓青.飞机总体参数设计与软件开发[D].西安:西北工业大学, 2003. Wang Xiaoqing. R esearch on aircraft conceptual parameters design and software development[D]. Xi′an: Northwestern Polytechnical University, 2003. |
 2016, Vol. 48
2016, Vol. 48