直升机的配平计算是直升机飞行动力学问题研究的基础,对直升机稳定性、操纵性分析、飞行品质评估和飞控系统开发均有重要意义。特别是直升机在复杂流场环境(如舰面流场)中飞行时,考虑旋翼桨叶的弹性变形、后行桨叶的动态失速等因素后,在直升机动态逆仿真及非线性控制设计过程中,直升机的动力学方程极其复杂,此时直升机配平计算的实质是求解高维复杂的非线性方程组,因此,研究非线性方程组的求解算法对解决直升机飞行动力学配平问题具有重要意义。为此,国内外不少学者做了大量研究。文献[1]采用牛顿法(Newton)配平简化模型,继而根据小扰动假设将运动方程线性化,进行后期的动力学分析。文献[2]提出了各种牛顿法的改进形式,文献[3]采用了广义梯度法(GRG),这两种方法收敛效率高,但依赖于初值的选取。文献[4]将梯度下降法与拟牛顿法(Quasi-Newton)相结合,降低了梯度法的初值敏感性,但大量的偏导数计算降低了求解效率。文献[5]先采用浮点遗传算法计算得到最优解,再利用Quasi-Newton法进行二次优化得到最终解,其实质仍然是Newton法。
大量研究表明,经典算法收敛快,精度高,但是其收敛性依赖于初值的选取,初值敏感性较高。近年来涌现的智能算法因其通用性好,全局寻优能力强,大量应用于优化领域,但也存在易陷入局部极值,局部搜索能力较差和精度不高等不足。因此,本文在结合经典算法与智能算法特点的基础上,提出了一种求解非线性方程组的新方法,即在粒子群(Particle swarm optimization,PSO) 算法的基础上,采用模拟退火(Simulated annealing,SA)算法的思想,在PSO搜索过程中嵌入Levenberg-marquardt(LM)优化算子,结合3种算法的优点以提高方程组求解的可靠性与计算效率,为直升机动力学方程组的求解提供一种新方法。
1 直升机配平方程组为突出配平算法的计算效率和准确性,本文采用一个高阶非线性飞行动力学模型[6-11]。具体的建模方法如下。
旋翼模型以叶素理论为基础,每片叶素的速度由机体运动速度、桨叶运动速度和旋翼诱导速度3部分确定,通过坐标转换得到叶素的速度分量,用以计算该片叶素处的合速度、当地马赫数、迎角、侧滑角及偏流角。
气动力模型方面采用准定常非线性气动力模型,每一片桨叶任一叶素的气动力均可通过关于叶素迎角、偏流角和马赫数的函数插值求得,并通过积分形式得到整个旋翼的气动载荷。
在桨叶运动方面采用了旋翼桨叶挥舞摆振耦合的刚性桨叶二阶动力学模型,并用一个经验公式模拟桨叶弹性扭转变形引起的桨距变化量;旋翼入流采用动态入流理论[9],能够模拟入流的动态响应过程。
机身、平尾和垂尾的气动载荷采用气动中心迎角、侧滑角查表函数的形式求得。尾桨采用Bailey模型[10] 进行计算。同时,采用经验公式模拟旋翼尾迹对机身、平尾、垂尾和尾桨,机身尾迹对平尾垂尾和尾桨的尾迹干扰。
上述模型具体的计算公式可参考文献,得到直升机的非线性状态方程组
| $\dot{X}=f\left( X,U,t \right)$ | (1) |
式中:U=[θcol,θlat, θlon,θped]T为操纵输入,分别对应旋翼总距、横向周期变距、纵向周期变距和尾桨总距;状态向量X定义为
| $\text{X= }\!\![\!\!\text{ }{{\text{X}}_{\text{bd}}}\text{,X}{{\text{ }\!\!~\!\!\text{ }}_{\text{flap}}}\text{,}{{\text{X}}_{\text{lag}}}\text{,}{{\text{X}}_{\text{ }\!\!~\!\!\text{ induced}}}\text{,}{{\text{X}}_{\text{MR}}}{{\text{ }\!\!]\!\!\text{ }}^{\text{T}}}$ | (2) |
式中:Xbd=[u,v,w,p,q,r,φb,φb,ψb]T为机体运动状态量,包括机体线速率、角速率和欧拉角;
本文以直升机悬停或匀速前飞状态为例,直升机状态导数
| $f({{x}_{j}})=_{0}^{2\pi }\dot{X}d\psi =0$ | (3) |
式中:xj(j=1,2,…,n)为配平方程组的解空间;n=17,包括θcol,θlat,θlon,θped,φb,φb,β0,β1c,β1s,ζ0,ζ1c,ζ1s,v0,vc,vs,vTR,θDytip等17个自由度。
据此构造目标函数
| $\text{fitness}=\text{Min}\sum\limits_{j=1}^{N}{{{f}_{j}}^{2}}({{x}_{1}},{{x}_{2}},\ldots ,{{x}_{n}})$ | (4) |
当变量xjk(j=1,2,…,n)的取值使fitness趋近零或最小值时,函数达到最优化,xk即方程组的最优解。
2 算法的描述与改进PSO算法是一种基于粒子群在多维搜索空间进行反复迭代搜索,寻找最优点的全局寻优方法[13]。针对PSO存在易陷入局部极小值,局部搜索能力较差和精度不高等不足,文献[14]给出了一种PSO-SA算法,即在PSO算法中引入SA算法。该算法通过退火温度T控制求解过程向最优值的优化方向进行,同时又以概率PT=e-Δf/Tk接受非最优解,因而具有跳出局部极值的能力,只要初始温度足够高,退火过程足够慢,算法就能收敛到全局最优解。
SA算法的引入虽然提高了跳出局部极值的能力,但是由于其局部搜索能力差,前一步跳出局部极值的粒子往往难以彻底摆脱局部极值的束缚,在尚未寻到下一个极值之前,又被重新吸进同一个局部极值的控制范围。因此,本文根据SA算法的思想,引进一个LM优化算子,在增强粒子的局部搜索能力的同时,提高粒子挣脱局部极值束缚的概率。
实现智能算法与经典算法的结合一般有两种思路,其一是通过智能算法进行一定程度的搜索,将结果作为智能算法的初值进行二次优化,其实质仍然是经典算法;其二是将经典算法作为一种局部搜索的工具,增强智能算法中个体的局部搜索能力,以提高个体跳出局部极值的能力,更利于寻到全局最优解。
本文侧重于后者,利用嵌入式LM优化算子在PSO搜索过程中进化粒子。根据PSO优化原理,所有粒子的参量均与处于最佳位置处粒子相关,故只需进化Pg位置处的粒子,即可改变种群中的所有粒子。为提高全局搜索能力,本文在选取进化粒子时,结合SA算法,采用轮盘赌的方法,即以概率随机选取进化粒子,其思路如下。
Tk温度下Pi处粒子被接受为最优的接受度pik=e-(pbesti-gbest)/Tk,Tk温度下该粒子被选中进行LM优化的概率
| ${{P}_{i}}^{k}=\frac{{{p}_{i}}^{k}}{\sum\limits_{j=1}^{N}{{{p}_{i}}^{k}}}$ | (5) |
当该粒子处于群体最佳位置时,接受度为最大值pgk=1,被选为优化粒子的概率最高;粒子偏离最佳位置越远,则接受度越小。在搜索初期,由于温度Tk较高,粒子接受度pik也较高,从而提高了处于非最佳位置的粒子被选中的概率,侧重于全局最优解的搜索;随着搜索过程的深入,Tk减少,粒子接受度pik也随之降低,处于最佳位置附近的粒子被选为进化粒子的概率增加,侧重于局部寻优的精度。
图 1给出了本文算法的流程图,同时为了便于比较,也列出了二次优化算法的流程图。
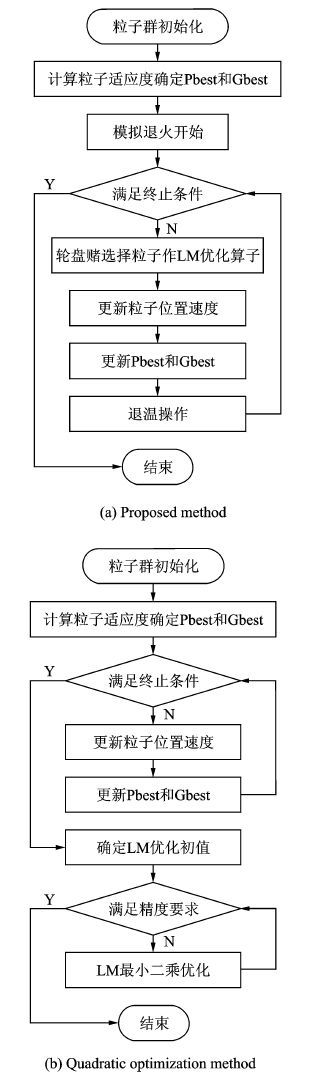
|
图 1 本文算法与二次优化算法计算流程图 Figure 1 Flowchart of proposed method and quadratic optimization method |
3 实例计算与分析 3.1 算例模型的验证
首先验证本文算例模型的准确性,计算UH-60A直升机悬停和匀速前飞状态下的配平计算结果,并与飞行实测数据[15]进行对比验证,如图 2所示。 UH-60A直升机全机、 旋翼、 尾桨和尾翼的具体数据参考文献[6],为了便于与飞测数据进行对比,驾驶员操纵输入以总距杆、驾驶杆和脚蹬行程百分比的形式给出。
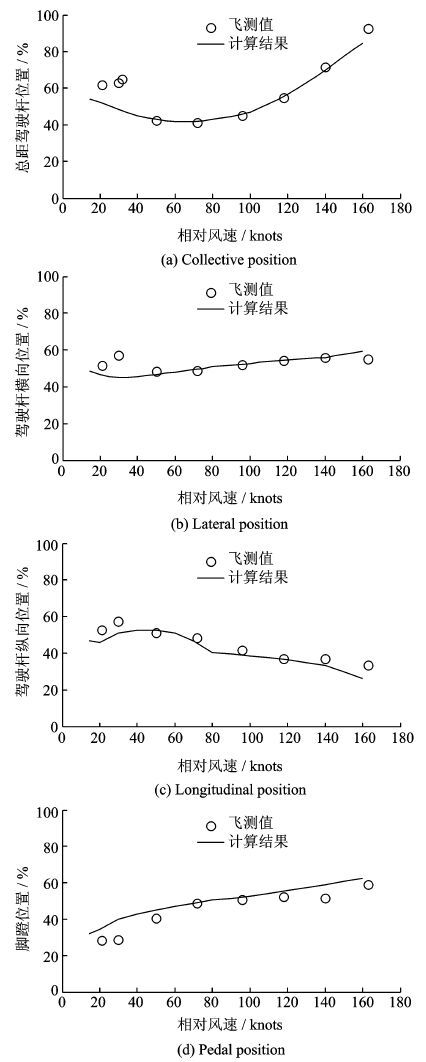
|
图 2 操纵量变化趋势 Figure 2 Variation trend of control sets |
由图 2可以看出,在悬停和低速前飞状态下,操纵量的计算结果与飞测数据存在一定的差距,主要是旋翼总距杆位置约有10%的最大误差,一方面是由于本文在直升机飞行动力学建模时采用了动态入流模型,该理论的基础是作用盘理论和加速度势理论,在悬停或低速飞行状态下,动态入流理论的假设条件并不完全成立,因此,其准确性一直都备受质疑;另一方面可能由飞测试验误差引起,因为悬停或小速度状态下直升机的动稳定性较差,驾驶员需要实时调整操纵量保持直升机的稳定,可能造成测量的误差。在中高速状态下则不存在这个问题,误差基本保持在5%以内,与飞行测试数据吻合较好。综上所述,本文建立的直升机飞行动力学模型具有较高的计算精度,基本满足了飞行动力学计算的需求。
3.2 算法效率以UH-60A直升机在某一飞行状态下的配平为例,研究本文配平算法的效率。在此,不妨在UH-60A直升机前飞速度vkt=140konts的状态下进行配平算法研究。由于该配平计算是求解17个自由度的高维复杂的非线性方程组,为了避免收敛到非物理解,需要对解空间进行约束。根据直升机的操纵极限与驾驶员的飞行经验设置3组解空间约束条件如下
(1)
| $\left\{ \begin{matrix} 9.9{}^\circ \le {{\theta }_{col}}\le 25.9{}^\circ ,-8{}^\circ \le {{\theta }_{lat}}\le 8{}^\circ \\ -12.5\text{ }{}^\circ \le {{\theta }_{lon}}\le 1\text{ }6.3{}^\circ ,4.5{}^\circ \le {{\theta }_{ped}}\le 36.5{}^\circ \\ 0\le {{v}_{0}}\le 20,0\le {{v}_{TR}}\le 40,-20\text{ }\le {{v}_{c,s}}~\le 20 \\ \begin{align} & -10{}^\circ \le {{\beta }_{0,1c,1s}}\le 10{}^\circ ,-10{}^\circ \le {{\zeta }_{0,1c,1s}}\le 10\text{ }{}^\circ \\ & -90{}^\circ \le \varphi {{~}_{b}},{{\varphi }_{b}}\le 90{}^\circ ,-10{}^\circ \le {{\theta }_{Dytip}}\le 10{}^\circ m/s \\ \end{align} \\ \end{matrix} \right.$ |
(2)
| $\left\{ \begin{array}{*{35}{l}} 9.9{}^\circ \le \text{ }{{\theta }_{col}}\le 25.9{}^\circ ,-8{}^\circ \le {{\theta }_{lat}}\le 8{}^\circ \\ -12.5{}^\circ \le {{\theta }_{lon}}\le 16.3{}^\circ ,4.5{}^\circ \text{ }\le {{\theta }_{ped}}\le 36.5{}^\circ \\ 0\le {{v}_{0}}\le 15,0\le {{v}_{TR}}\le 20,-10\le {{v}_{c,s}}\le 10 \\ -\text{ }5{}^\circ \le {{\beta }_{0,1c,1s}}\le 5{}^\circ ,-5{}^\circ \le {{\zeta }_{0,1c,1s}}\le 5{}^\circ \\ -10{}^\circ \text{ }\le {{\varphi }_{b}},{{\varphi }_{b}}\le 10{}^\circ ,-5{}^\circ \le {{\theta }_{Dytip}}\le 5{}^\circ m/s \\ \end{array} \right.$ |
(3)
| $\left\{ \begin{array}{*{35}{l}} 15{}^\circ \le {{\theta }_{col}}\le 22{}^\circ ,\text{ }-2{}^\circ \le {{\theta }_{lat}}\le 2{}^\circ \\ 8{}^\circ \le {{\theta }_{lon}}\le 12{}^\circ ,10{}^\circ \le {{\theta }_{~ped}}\le 25{}^\circ \\ 0\le {{v}_{0}}\le 5,0\le {{v}_{TR}}\le 10,-5\le {{v}_{c,s}}\le 5 \\ -5{}^\circ \le {{\beta }_{0,1c,1s~}}\le 5{}^\circ \text{ },-5{}^\circ \le \text{ }{{\zeta }_{0,1c,1s}}\le 5{}^\circ \\ -5{}^\circ \le {{\varphi }_{b}},{{\varphi }_{b}}\le 5{}^\circ ,-5{}^\circ \le {{\theta }_{Dyt\text{ }ip~}}\le 5{}^\circ \text{ }m/s \\ \end{array} \right.$ |
对于以上算例,本文均采用Matlab7.0编制程序。LM算法、PSO算法、二次优化算法与本文算法的主要参数设置如下:PSO算法中加速因子c1=c2=1.496 2,惯性权重wmin=0.4,wmax=0.9,种群数N=40,最大迭代步数Maxgen=200,其中二次优化算法中PSO迭代步数设为50;LM算法中初始阻尼常数μ0=0.01,阻尼因子βmin=1,βmax=10,其中单独LM算法的初值随机。迭代精度设为e<10-12(即max|fi|<10-6)。对测试方程组分别采用4种算法各实验200次,得到了关于收敛可靠性(即求解成功率)和求解效率的相关数据,具体见表 1,2。
| 表 1 收敛可靠性对比 Table 1 Contrast of convergence reliability |
| 表 2 求解效率对比 Table 2 Contrast of solving efficiency |
算法的收敛可靠性是衡量方程组求解算法的首要指标,分析表 1可知,PSO算法和LM算法处理高维复杂的直升机非线性方程组的收敛可靠性不高;二次优化算法由于其核心仍是LM算法,因此其求解成功率与LM算法相当,收敛可靠性依然不够理想;本文算法在解空间约束扩大的情况下,其求解成功率都达到了100%,明显高于其他几种算法,表明嵌入LM优化算子确实能提高PSO算法的求解成功率。
求解效率也是衡量方程组求解算法的重要指标。由于单独PSO算法的收敛可靠性为0,只选取其余3种算法作效率对比,统计上述200次实验,以求解成功一次所需的计算机平均运行时间作为算法效率对比的主要指标,其中,求解失败的实验不计入计算时间。由表 2可知,LM算法的求解效率较高,且其计算效率与解空间约束相关,解空间越明确,该算法的计算效率越高;二次优化算法由于在进行LM优化之前,需利用PSO算法进行初值的筛选,因此其效率明显较另外二者低;本文算法在保证算法收敛的前提下,对解空间约束的依赖性较低,计算效率相对稳定。
综上所述,在处理直升机配平问题时,初值对算法求解的影响很大,在解空间约束较为明确的情况下,各类算法均具有较强的收敛能力,其中LM算法的求解效率要明显高于混合算法;而在解空间约束放宽的情况下,LM算法和二次优化算法的收敛能力均有一定程度的下降,而本文算法则保持了100%的收敛成功率,体现了较强的大范围搜索能力。
4 结论(1) 本文针对复杂多维的直升机配平问题,设计了一种嵌入LM优化算子的新粒子群算法,即在PSO 算法的基础上,根据SA算法思想,嵌入LM优化算子。该算法充分发挥了PSO算法的全局收敛性,SA算法易跳出局部极值的特点和LM算法的收敛速度快和精度高等优势。
(2) 计算并分析了UH-60A直升机在悬停和前飞状态下的操纵量和姿态角,验证了本文算例模型。
(3) 针对UH-60A直升机在某一前飞状态的配平,通过与LM算法、PSO算法和二次优化算法的比较,表明本文算法收敛可靠,求解效率高,对于高维复杂的直升机非线性方程组求解问题具有良好的适应性。
| [1] |
高正, 陈仁良.
直升机飞行动力学[M]. 北京: 科学出版 社, 2003 .
Gao Zheng, Chen Renliang. Helicopter flight dynamics[M]. Beijing : Science Press, 2003 . |
| [2] | Burden R L, Faires J D. Numerical analysis[M]. Seventh Edition. US: Brooks/Cole Cengage Learing, 2001 . |
| [3] | Schank T C, Optimal aer oelastic trim for rotorcraft with constrained non-unique trim solutions[D]. G erogia: G eorgia Institute of Technology, 2008. |
| [4] | Subramanian S, Gaonkar G H, Maier T H. A theoretical and experimental investigation of hingeless-rotor stabili t y and trim[C]//23rd European Rotorcraft Forum, US: Brooks/Cole Cengage Learni ng. Dresden, Germany: European Rotrocraft International, 1997. |
| [5] |
代冀阳, 吴国辉, 朱国民.
适于直升机配平计算的混合遗传算法[J]. 飞行力学 , 2010, 28 (1) : 24–28.
Dai Jiyang, Wu Guohui, Zhu Guomin. Equilibrium computation of helicopters used by hybrid genetic algorithm[J]. Flight Dynamics , 2010, 28 (1) : 24–28. |
| [6] | Howlett J J. UH-60A black hawk engineering simula tion program[R]. NASA-CR-166309, 1981. |
| [7] | Kim F D. Formulation and valida tion of high-order mathematical models of helicopter flight dynamics[D]. Mar yland: University of Maryland, 1994. |
| [8] |
李攀.旋翼非定常自由尾迹及高置信度直升机飞行动力学建模研究[ D].南京:南京航空航天大学, 2010. Li Pan. Rotor unsteady free-vortex wake mode l and investigation on high-fidelity modeling of helicopter flight dynamics[D ] . Nanjing: Nanjing University of Aeronautics & Astronautics, 2010. |
| [9] | Pitt D M, Peters D A. Theoretical prediction of dynamic inflow deriva tives[J]. Vertica , 1981, 5 (1) : 21–34. |
| [10] | Bailey F J. A simplified theoretic al method of determining the characteristics of a lifting rotor in forward fligh t[R]. NASA-TR-716, 1941. |
| [11] |
陈仁良, 辛冀, 李攀.
一种新的尾迹-地面干扰修 正方法[J]. 南京航空航天大学学报 , 2012, 44 (5) : 694–699.
Chen Renliang, Xin Ji, Li Pan. New rectification method for interaction of rotor wake vortices and gr ound[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2012, 44 (5) : 694–699. |
| [12] | Celi R. Effects of hingeless rotor aeroelasticity on heli copter longitudinal flight dynamics[C]//Proceedings of the 47th Annual Forum of the American Helicopter Society. Phoenix, Anizona: American Helicopter Society International, 1991. |
| [13] | 刘楠, 黄金泉. 应用改进 粒子群算法的涡轴发动机性能寻优[J]. 南京航空航天大学学报 , 2013, 45 (3) : 303–308. |
| [14] |
王凌, 刘波.
微粒 群优化与调度算法[M]. 北京: 清华大学出版社, 2008 : 36 -56.
Wang Ling, Liu Bo. Pa rticle swarm optimization and scheduling algorithms[M]. Beijing: Tsinghua Univ ersity Press, 2008 : 36 -56. |
| [15] | Ballin M G. Validation of a real -time engineering simulation of the UH-60A helicopter[R]. NASA-TM-88360, 1 987. |
 2016, Vol. 48
2016, Vol. 48


