2. 南京航空航天大学飞行器先进设计技术国防重点学科实验室,南京, 210016
2. Key Laboratory of Fundamental Science for National Defense-Advanced Design Technology of Flight Vehicle, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China
现代客机绝大多数采用涡扇发动机作为推进系统,对发动机选型或提出设计要求是飞机总体设计中最重要的工作之一。飞机总体设计所需要的推进系统数据通常包括发动机特性、质量以及特征尺寸[1]。发动机特性主要指推力与油耗的速度、高度和节流(油门)特性,是飞机飞行性能计算所必需的数据;质量包括发动机裸机、附件、短舱以及挂架等各部件质量,是飞机总质量的组成要素;特征尺寸主要指发动机短舱的长度和最大直径,是发动机安装或短舱设计所需要的数据[1-3]。其中,发动机特性数据通常表示为与高度、速度和油门位置相对应的3维数据表格形式,分别构成推力与耗油率的数据模型。
飞机总体设计中最先确定的发动机参数通常是起飞需用推力,以此为基础可以逐步确定适合飞机总体方案的发动机参数组合[3-4],这一过程需要发动机特性、质量和特征尺寸等各项完备数据的支持。这一阶段获取发动机完备数据的途径通常有3种[1, 4]:(1) 选取使用推力相近的已有发动机数据;(2) 使用基准发动机数据在一定条件下按比例缩放或采用某种数学算法拟合,即“橡皮发动机”模型(Rubber engine)[1, 4-6];(3) 基于发动机总体循环参数的分析模型,即“参数平台”(Parametric deck)[4, 7-8]。第1,2类数据获取方式仅适合于飞机最早的初始概念设计与分析过程,且只在一定的推力范围内有效[4, 6];第3类分析模型适合于飞机总体分析与发动机选型的全过程[7-8],也可以应用于发动机循环参数的初步选取以及发动机性能衰减的分析[9-10]。基于循环参数的分析模型又包括工程分析模型(按工作原理简化)[3, 11]和零维分析模型(根据轴流剖面的部件特性参数逐级推算)两类[7-8]。涡扇发动机的总体循环参数主要指涵道比(Bypass ratio,BPR) μBPR、总压比μOPR、比推力μST和涡轮前温度TTE等几项[1]。工程分析模型的运行和求解只需要这4个基本的总体循环参数,且分析速度较快,适合于总体分析中的快速迭代和优化;零维分析模型的运行参数除总体循环参数以外,还包括各特征剖面部件的循环技术参数,分析速度较慢,适合于发动机循环参数与部件技术要求的初步选取[8, 12]。
在总体初步设计阶段,需要对大量设计方案进行评估,并初步确定发动机的总体循环参数。因此,计算速度快、数据需求少的工程分析模型在这一阶段的应用中具有优势。本文以常规涡喷发动机估算模型为基础,引入涡扇发动机特有的热流动循环原理对原模型进行必要的修正,给出一种基于总体循环参数的涡扇发动机工程分析模型建立方法。
1 循环参数分析发动机对空气做功产生的推力由两个来源组成,即空气流过发动机后的动量变化和尾喷口的排气压力。推力产生的基本原理如下[1]
| $F={{q}_{\text{m}}}{{V}_{\text{j}}}-{{V}_{0}}+{{p}_{\text{j}}}-{{p}_{0}}{{A}_{\text{j}}}$ | (1) |
式中:qm为空气质量流量,Vj为喷口处喷流速度,V0为进气口来流速度(即飞行速度),pj为尾喷口排气压强,p0为当前状态大气压强,Aj为尾喷口的横截面积。式中忽略了因燃油与空气混合使空气质量略有增加而对动量变化产生的影响。若喷口压力充分膨胀,可以认为进气与排气的压强相等,则式中的排气压力项不存在,推力公式简化为:F=qmVj-V0。
由推力基本公式可以看出,高喷流速度、低质量流量或者低喷流速度、高质量流量可以得到相同的推力输出。然而,低喷流速度的发动机受进气速度的影响更大,当飞行速度增大时这类发动机的推力随飞行速度的衰减更快。比推力表示为发动机推力与对应的空气质量流量之比,即μST=F/(qm·g),其中g为重力加速度。可以看出,推力相同的情况下,比推力高的发动机喷流速度高而空气质量流量小。对于涡扇发动机,比推力的大小与涵道比和总压比直接相关,利用现有发动机的统计数据可以近似确定三者之间的关系。部分现有涡扇发动机的主要总体循环参数(起飞状态)如表 1所示[1, 13]。
| 表 1 部分现有涡扇发动机的主要总体循环参数 Table 1 Main cycle parameters of some turbofan engines |
从表 1可以看出,各个型号发动机对应的循环参数是一批离散的数据点,要得到涵道比、总压比与比推力的对应关系需要对这些数据点进行离散插值[14]。通过离散插值可以将这些数据转化为标准参数取值点对应的数据,并拟合成统计关系表达式
| $\begin{align} & {{\mu }_{\text{ST}}}=1+29.02\times \exp \left[ a\mu _{\text{BPR}}^{2}+b\mu _{\text{OPR}}^{2} \right] \\ & a=-0.008\text{ }8\text{ }b=3.86\times {{10}^{-4}} \\ \end{align}$ | (2) |
以表 1中的数据测试式(2) 的拟合效果,其平均误差为2.18%,最大误差为4.70%,可以满足总体设计阶段对发动机相关参数的精度要求。由表 1中的数据以及式(2) 所显示的关系可以看出,提高涵道比可以显著降低比推力,即在同等推力的情况下增加了发动机的空气质量流量。而从统计关系上看,总压比对起飞状态比推力的影响很小。
2 推力特性模型发动机的推力特性可以表示为发动机在不同飞行状态下的推力与最大油门状态下的海平面静推力(Sea-level static thrust,SLST)F0之间的相对比例,这一比例与飞行高度、速度和油门位置之间具有一定的函数关系。
2.1 高度与速度特性涡扇发动机的推力随高度增加和速度增大而衰减,某一飞行高度和速度下的实际推力与海平面最大静推力的比例可以表示为高度和速度的函数。对于涡喷发动机或小涵道比(μBPR<3) 的涡扇发动机,当前推力与飞行高度和速度之间的关系可以表示为[15]
| $\begin{align} & F={{F}_{0}}+\left\{ 1+\exp \left[ -\left( {{k}_{1}}+{{k}_{2}}h \right){{F}_{0}} \right] \right\}{{k}_{3}}\cdot \\ & \exp -{{k}_{4}}h+{{k}_{5}}V\exp -{{k}_{6}}h \\ \end{align}$ | (3) |
式中:F0为海平面最大静推力,V为当前飞行速度,h为当前高度。各系数项的取值分别为:k1=0.259,k2=2.20×10-4,k3=0.993 6,k4=2.87×10-3,k5=1.44×10-3,k6=1.80×10-3。
这一关系式只反映了一般喷气式发动机推力的高度与速度特性,没有反映出比推力对发动机推力特性的影响,需要进行相应的修正。如前所述,比推力低的发动机喷流速度低,因而其推力随飞行速度的增大衰减更快。可以认为,在其他状态一致时,要产生相同的推力,比推力低的发动机飞行速度应该小一些。因此,可以在式(3) 的基础上对飞行速度项加以修正,从而体现比推力的影响。比推力与喷流速度的关系如下
| ${{V}_{\text{j}}}={{\mu }_{\text{ST}}}g+{{V}_{0}}$ | (4) |
从式(4) 可以看出,根据比推力和当前的飞行速度即可以求得对应的喷流速度。式(3) 中的速度项可以通过喷流速度进行修正
| $V={{V}_{0}}\left[ 1+a\sigma /\left( {{V}_{0}}+{{V}_{j}} \right) \right]$ | (5) |
式中:a为当前高度对应的声速,σ为当前高度的空气相对密度。对当前飞行速度经过式(4,5) 修正后再代入式(3) ,计算得到的推力特性即包含了比推力的影响。
2.2 油门特性通过油门杆可以控制发动机的转速,从而改变发动机的推力。油门可以在几个特殊挡位之间连续变化。几个特殊挡位主要指最大工作状态(最大起飞推力状态)、最大连续工作状态、最大爬升状态、最大巡航状态和慢车状态等[1, 3, 15]。在油门、转速与推力三者之间没有确定关系式的情况下,可以近似认为油门是线性的,即认为推力随油门位置按正比关系增长。几个特殊挡位对应的比例系数可以根据不同的发动机型号或使用情况做出调整,通常情况下,比例系数的选取可以参照表 2[3]。
| 表 2 涡扇发动机典型油门位置对应的比例系数参考值 Table 2 Typical reference ratio of turbofan engine throttle |
其他连续挡位的推力特性数据可以通过在特殊挡位数据的基础上插值获取,以满足不同飞行状态下计算的需要。
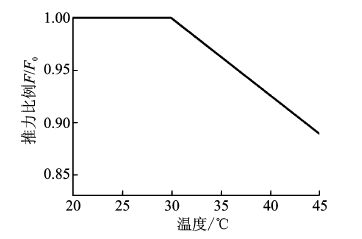
2.3 环境温度的影响工作温度也会影响发动机的推力,当进气温度(环境温度)超过一定温度时,发动机的推力会随着温度的升高而减小,二者基本表现为线性关系。典型的涡扇发动机推力受环境温度影响的变化趋势如图 1所示,图中给出了推力比例系数与温度的对应关系[16]。从图中可以看出,典型的起作用温度约为30 ℃ (忽略涡轮前温度变化的影响),超过这一温度后,发动机推力比例系数呈线性下降。
|
图 1 涡扇发动机海平面静推力随环境温度变化的典型曲线 Figure 1 Typical trend data of turbofan SLST flat rating |
根据图 1中的数据,可以得出环境温度增量与发动机推力比例系数之间的近似关系表达式
| ${{K}_{T}}=1.203-0.006\text{ }767\times \left( 30+\Delta T \right)$ | (6) |
式中ΔT为当前环境温度高于典型环境温度的增量。
3 油耗特性模型发动机的油耗与效率直接相关,总效率越高,发动机的单位推力油耗就越低。在总效率分析方法的基础上,可以建立涡扇发动机的耗油率分析模型。
3.1 发动机的总效率发动机的总效率可以分解为3个主要组成部分[1],燃气发生器的效率ηth、涡轮传输系统的效率ηtr以及推进喷流系统的效率ηp。总效率ηo可以表示为
| ${{\eta }_{\text{o}}}={{\eta }_{\text{th}}}\cdot {{\eta }_{\text{tr}}}\cdot {{\eta }_{\text{p}}}$ | (7) |
热效率的计算公式如下[1]
| ${{\eta }_{\text{th}}}=1-{{\left( 1/{{\mu }_{\text{OPR}}} \right)}^{n}}$ | (8) |
式中:n为燃气多变指数γ的函数,表示为n=γ-1/γ。多变指数γ受到涡轮前温度和总压比的影响,不同工况下的对应取值约在1.05~1.25之间,初步估算可以取为1.20。一般情况下,提高总增压比和涡轮前温度且两者在合理区间范围内匹配,可以达到提高热效率从而降低油耗的效果。
传输效率的计算公式如下[1]
| ${{\eta }_{\text{tr}}}=\left( 1+{{\mu }_{\text{BPR}}} \right)/\left( 1+{{\mu }_{\text{BPR}}}/{{\eta }_{\text{f}}}{{\eta }_{\text{t}}} \right)$ | (9) |
式中:ηf为风扇效率,ηt为涡轮效率。由式(9) 可以看出,发动机的传输效率主要取决于涵道比、风扇效率和涡轮效率。现代涡扇发动机的风扇效率和涡轮效率通常在80%~95%之间,在没有具体数值的情况下可以取85%(早期水平)或90%(新技术水平)作为估计值。
推进效率由下面的公式确定[1]
| ${{\eta }_{\text{p}}}=2{{V}_{0}}/\left( {{\mu }_{\text{ST}}}g+2{{V}_{0}} \right)$ | (10) |
从式(10) 可以看出,比推力小的发动机推进效率高。
3.2 耗油率及其修正发动机的耗油率(Specific fuel consumption,SFC)定义为单位推力下的燃油流量,其量纲(N/N/h)表示为时间的倒数(1/h),与推力和燃油质量的量纲无关。理想状态下(即发动机效率为100%)的耗油率只与飞行马赫数有关[1],约为0.25 Ma。在设计点状态下,可以根据发动机的总效率估算发动机的耗油率[1]
| ${{C}_{0}}=\frac{Ma}{4{{\eta }_{o}}}$ | (11) |
设计点状态指发动机设计时所选定的典型工作状态,对应典型的飞行高度和速度。发动机主要工作在设计点状态及其附近,由对应的飞行高度和速度可以确定设计点状态的效率和耗油率,进而可以计算出非设计点状态的耗油率[3]
| ${{C}_{\text{OD}}}={{C}_{0}}\left[ 1+0.01\left( {{T}_{\text{c}}}/{{T}_{\text{OD}}}-1 \right) \right]$ | (12) |
式中Tc和TOD分别为当前状态的推力和设计点状态的推力。
由式(12) 所得到的非设计点耗油率考虑了包含装机和引气影响在内的极端情况,实际耗油率略小于该值;同时,实际耗油率随飞行高度和速度的变化而变化,变化规律还受到涵道比的影响,它们之间的函数关系为[3]
| $\begin{align} & {{C}_{\text{sfc}}}={{C}_{\text{OD}}}\left( 1-0.15\mu _{\text{BPR}}^{0.65} \right)\times \\ & \left[ 1+0.28\left( 1+0.063\mu _{\text{BPR}}^{2} \right)Ma \right]{{\sigma }^{0.08}} \\ \end{align}$ | (13) |
从式(13) 中可以看出,实际耗油率主要与涵道比、飞行高度和速度有关。
由上述公式建立的分析模型可以获得发动机随飞行高度和速度变化的耗油率曲线,分析所得的耗油率考虑了发动机的涵道比、总压比和比推力的影响。
4 分析模型的验证选取两种典型涡扇发动机特性曲线作为涡扇分析模型的验证依据[1, 13],所选两种发动机的涵道比分别为6.5和13.0,均为高涵道比涡扇发动机。选取典型的工作点状态,对分析模型所输出的推力与油耗特性数据分别进行验证。
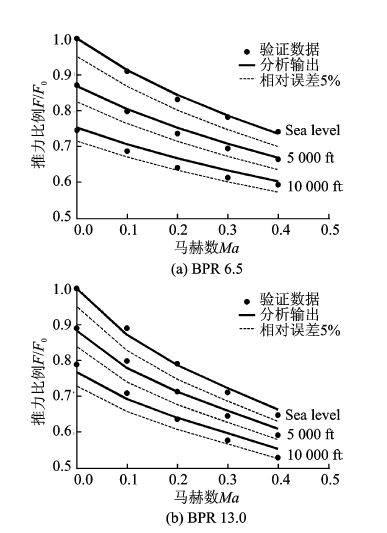
4.1 推力特性的验证分析模型输出的起飞状态推力曲线及其与验证数据点的对比如图 2所示,图中分别给出了海平面(Sea level)、5 000和10 000 ft等高度对应的发动机推力特性。
|
图 2 起飞状态推力特性验证 Figure 2 Verification of take-off thrust |
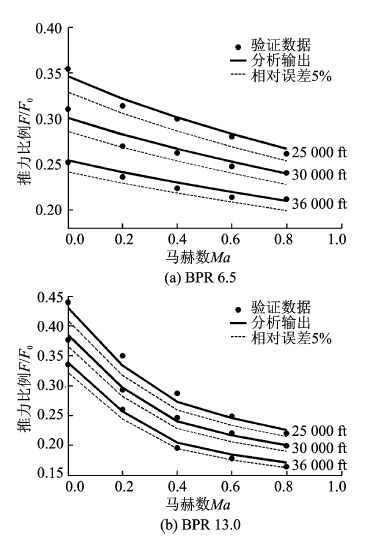
分析模型输出的最大巡航状态推力曲线及其与验证数据点的对比如图 3所示,图中分别给出了25 000,30 000和36 000 ft等高度对应的发动机推力特性。
|
图 3 最大巡航状态推力特性验证 Figure 3 Verification of the maximum cruise thrust |
由图 2,3的对比分析可以看出,涡扇分析模型输出的推力特性曲线与验证数据点的变化趋势相一致,而且典型状态点的计算值与验证数据非常接近,相对误差均能够保持在5%以下,可以满足客机总体分析阶段对于推力特性模型的精度要求。
选取典型状态点的数据进行具体对比及精度分析,如表 3所示。从表中的数据可以看出,与验证数据相比,模型输出的推力特性计算值在不同高度、速度和推力状态下均能够获得较高的分析精度,最大相对误差分别为3.90%(BPR 6.5) 和4.63%(BPR 13.0) 。数据对比充分表明,模型分析输出的推力特性具有非常高的准确性。
| 表 3 推力特性数据的验证对比 Table 3 Verification and comparison of thrust data |
4.2 油耗特性的验证
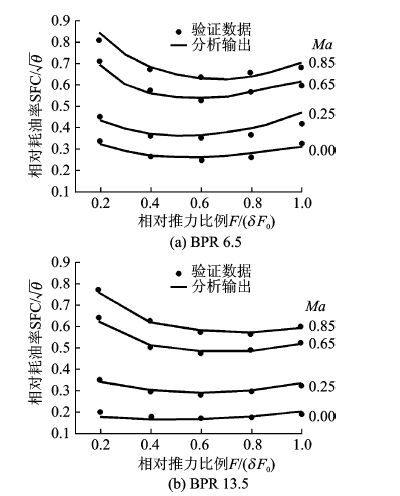
为了准确评价不同使用环境下发动机的油耗特性,需要引入针对燃气涡轮发动机的通用特性处理方法[17],将发动机的耗油率和推力分别相对于外界大气温度和压强进行相应转化,从而获取相对耗油率(SFC/$\sqrt{\theta }$)与相对推力比例(F/(δF0))之间的关系,表示为耗油率回归曲线[18]。其中,θ为使用环境温度与海平面标准大气温度之比;δ为使用环境的气压与海平面标准气压之比。涡扇分析模型输出的耗油率回归曲线如图 4所示。
|
图 4 耗油率回归曲线验证 Figure 4 Verification of SFC loops |
从图 4可以看出,分析得到的耗油率变化曲线与验证数据点基本重合,部分低速高推力状态数据误差较大。进一步选取典型数据点进行对比分析,如表 4所示。
| 表 4 分析模型油耗特性的数据对比 Table 4 Verification and comparison of SFC loops data |
通过表 4数据可以看出,在绝大部分状态点,计算值与验证数据之间的相对误差较小,可以控制在4%以内。涵道比6.5的发动机算例中,马赫数在0.25、推力比例在0.8时的高推力状态计算值误差较大,达到8.17%;但该误差为正向偏差值,表明其计算结果偏保守,在总体分析阶段这类误差也处于可以接受的范围。总地来看,模型分析输出的涡扇发动机油耗特性数据保证了较高的准确性。
5 结束语以燃气涡轮发动机的估算模型为基础,结合涡轮风扇发动机的循环原理对估算模型进行修正,建立了基于总体循环参数的涡扇发动机工程分析模型。这种分析模型的精度可以满足飞机总体设计阶段对发动机特性数据精度的要求,而且具有计算速度快、需求参数少的优点,因此特别适合于飞机总体设计阶段对推进系统进行参数分析与方案评估应用。
| [1] | Jenkinson L R, Simpkin P, Rhodes D. Civil jet aircraft design[M]. London: Arnold, 1999 : 181 -222. |
| [2] |
余雄庆, 欧阳星, 王宇, 等.
用适用性理念指导短程客机概念设计[J]. 南京航空航天大学学报 , 2014, 46 (3) : 349–354.
Yu Xiongqing, Ouyang Xing, Wang Yu, et al. Adaptability inspired conceptual design of short-haul civil jets[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2014, 46 (3) : 349–354. |
| [3] | Howe D. Aircraft conceptual design synthesis[M]. London and Bury St Edmunds: Professional Engineering Publishing Ltd, 2000 : 53 -78. |
| [4] | Raymer D P. Aircraft design: a conceptual approach[M]. Reston: AIAA Inc, 1999 : 193 -220. |
| [5] |
叶志锋, 杨固东, 苏伟生.
基于试车数据的发动机神经网络模型[J]. 南京航空航天大学学报 , 2007, 39 (1) : 26–29.
Ye Zhifeng, Yang Gudong, Su Weisheng. Neural network model of Aeroengine based on experimental data[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2007, 39 (1) : 26–29. |
| [6] | Svoboda C. Turbofan engine database as a preliminary design tool[J]. Aircraft Design , 2000, 3 (1) : 17–31. DOI:10.1016/S1369-8869(99)00021-X |
| [7] | Mink G, Behbahani A. The AFRL ICF generic gas turbine engine model [R]. AIAA-2005-4538, 2005. |
| [8] | Osterbeck P, Butzin E L, Johnson P. Air vehicle sizing and performance modeling in NPSS [R]. AIAA-2009-5417, 2009. |
| [9] | Wang Jiankang, Zhang Haibo, Sun Jianguo, et al. Application of hybrid aero-engine model for integrated flight/propulsion optimal control[J]. Transactions of Nanjing University of Aeronautics & Astronautics , 2012, 29 (1) : 16–24. |
| [10] |
赵运生, 胡骏, 屠宝锋, 等.
部件老化对大涵道比涡扇发动机性能影响仿真[J]. 南京航空航天大学学报 , 2013, 45 (4) : 447–452.
Zhao Yunsheng, Hu Jun, Tu Baofeng. Simulation of component deterioration effect on performance of high bypass ratio turbofan engine[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2013, 45 (4) : 447–452. |
| [11] |
周文祥, 黄金泉, 黄开明.
航空发动机简化实时模型仿真研究[J]. 南京航空航天大学学报 , 2005, 37 (2) : 251–255.
Zhou Wenxiang, Huang Jinquan, Huang Kaiming. Real-time simulation system for aeroengine based on simplified model[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2005, 37 (2) : 251–255. |
| [12] | Lytle J K. Multi-fidelity simulations of air breathing propulsion systems [R]. AIAA-2006-4967, 2006. |
| [13] | Jenkinson L R, Simpkin P, Rhodes D. Civil jet aircraft design, data sets-data B [DB/OL]. (2001-01-01)[2015-06-20]. http://www.elsevierdirect.com/companions/9780340741528/appendices/data-b/default.htm. |
| [14] | Kouibia A, Pasadas M, Rodriguez M L. Numerical approximation by discrete interpolating variational splines[J]. Applied Numerical Mathematics , 2012, 62 (9) : 1109–1118. DOI:10.1016/j.apnum.2011.03.011 |
| [15] | Isikveren A T. Quasi-analytical modelling and optimisation techniques for transport aircraft design [D]. Stockholm, Sweden: Royal Institute of Technology (KTH), 2002. |
| [16] | Schaufele R D. The elements of aircraft preliminary design[M]. Santa Ana, CA: Aries Publications, 2000 : 176 -181. |
| [17] |
尚义.
航空燃气涡轮发动机[M]. 北京: 航空工业出版社, 1995 : 130 -133.
Shang Yi. Aero gas turbine engine[M]. Beijing: Aviation Industry Press, 1995 : 130 -133. |
| [18] | Wikiversity. Jet engine performance notes [EB/OL].(2014-11-22)[2015-06-20]. https://en.wikiversity.org/wiki/Jet_engine_performance_notes. |
 2016, Vol. 48
2016, Vol. 48


