2. 中国人民解放军95507部队, 贵阳, 550031
2. 95507 Army, Chinese People′s Liberation Army, Guiyang, 550031
无铰式旋翼取消了挥舞铰和摆振铰,大大简化了旋翼结构,但是,桨叶翼型段与变距轴承之间采用了复合材料柔性段。特别地,新型无铰式旋翼桨毂与桨叶之间采用多路传力结构,如“虎”式直升机,其多个弹性轴承在实现变距运动的同时,为桨叶挥舞和摆振运动提供刚性约束,存在复杂的载荷平衡关系。柔性段和变距轴承的综合作用使得旋翼桨叶存在显著的非线性大变形及强烈的结构耦合,因而这种旋翼构型的气动弹性稳定性问题尤为突出,是目前旋翼动力学研究中的热点与难点之一。
1974年Hodges等人提出了中等变形梁理论,建立了非均匀有预扭的旋转细长桨叶的挥/摆/扭弹性耦合方程[1]。1990年,Hodges[2-3]等人又提出了一种适合于复合材料无铰式旋翼桨叶动力学分析的非线性几何精确旋转梁模型,采用一维广义Jaumann-biot-Cauchy应变张量,引入罗德里格斯参数表征桨叶剖面整体大转动,完整地保留了几何非线性成分,进一步提高了无铰式旋翼动力学分析精度的要求。
本文以Hodges全本征桨叶动力学方程、Peters动态入流模型[4]以及Leishman-Beddoes非定常气动力模型[5-6]为基础,建立了无铰式旋翼气弹耦合分析模型,并针对无铰式旋翼构型“多路传力”的特点细化桨毂边界条件,得到了适用于新型无铰式旋翼气动弹性分析的非线性混合变量状态空间方程,最后将该模型应用于无铰式旋翼气动弹性响应计算和稳定性分析中,验证了该模型的有效性和准确性。
1 新型无铰式旋翼气动弹性综合分析模型 1.1 无铰式旋翼动力学分析综合方程 1.1.1 大变形桨叶/柔性梁结构的全本征方程若桨叶单位长度的动能和应变能分别为K和U,则应变能对广义力应变γ,广义力矩应变κ的偏导数分别为桨叶剖面的合内力F和合内力矩M
| $F = {\left( {{{\partial U} \over {\partial \gamma }}} \right)^T},M = {\left( {{{\partial U} \over {\partial \kappa }}} \right)^T}$ | (1) |
引入桨叶剖面动量P和动量矩H
| $\begin{align} & P={{\left( \partial K/\partial V \right)}^{T}}=\mu \left( V-\tilde{\bar{\xi }}V \right) \\ & H={{\left( \partial K/\partial \Omega \right)}^{T}}=i\Omega +\mu \tilde{\bar{\xi }}V \\ \end{align}$ | (2) |
式中:μ,μξ,i分别为桨叶单位长度的质量、静矩、质量惯性矩;V为速度矩阵;Ω为角速度矩阵。文中运算符“~”的定义如下:
| $\tilde{\bar{\xi }}=\left[ \begin{matrix} 0 & -{{\xi }_{3}} & {{\xi }_{2}} \\ {{\xi }_{3}} & 0 & -{{\xi }_{1}} \\ -{{\xi }_{2}} & {{\xi }_{1}} & 0 \\ \end{matrix} \right]$ | (3) |
若f和m分别为桨叶变形后坐标系B下桨叶单位长度受到的分布力和分布力矩,则根据哈密尔顿原理可以得到桨叶/柔性梁结构的广义力与力矩平衡
| $\begin{align} & F\prime +\tilde{K}F+f=\dot{P}+\tilde{\Omega }P \\ & M\prime +\tilde{K}M+({{{\tilde{e}}}_{1}}+\tilde{\gamma })F+m=\dot{H}+\tilde{\Omega }H+\tilde{V}P \\ \end{align}$ | (4) |
式中:K为变形后梁参考轴线的曲率矢量。广义力应变γ和广义力矩应变κ通过桨叶剖面柔度特性R(x1),S(x1),T(x1)与桨叶剖面力F和力矩M联系起来。
类似的,桨叶剖面动量P和动量矩H与速度和角速度的关系方程为
| $\left[ {\matrix{ P \cr H \cr } } \right] = \left[ {\matrix{ {\mu \Delta } & { - \mu \tilde{\bar{\xi }}\ } \cr {\mu \tilde{\bar{\xi }}\ } & I \cr } } \right]\left[ {\matrix{ V \cr \Omega \cr } } \right] = \left[ {\matrix{ G & {{K_1}} \cr {K_1^T} & I \cr } } \right]\left[ {\matrix{ V \cr \Omega \cr } } \right]$ | (5) |
式中:G为线密度对角阵;K1为参考轴线至剖面质心的距离;I为剖面的惯性矩阵;Δ为3阶单位矩阵。
根据广义应变-位移关系和速度-位移关系,消去位移和转动项得到全本征运动方程
| $V\prime +\tilde{K}V+\left( {{{\tilde{e}}}_{1}}+\tilde{\gamma } \right)\Omega =\dot{\gamma }$ | (6) |
| $\Omega \prime +\tilde{K}\Omega =\dot{\kappa }$ | (7) |
式中
联立式(1~7) ,得到直升机(非均匀、带预扭、预弯及各向异性)桨叶的非线性全本征混合动力学方程,具体形式参考文献[7, 8]。
1.1.2 边界约束条件如图 1所示,新型无铰式旋翼构型是典型的多路传力构型。
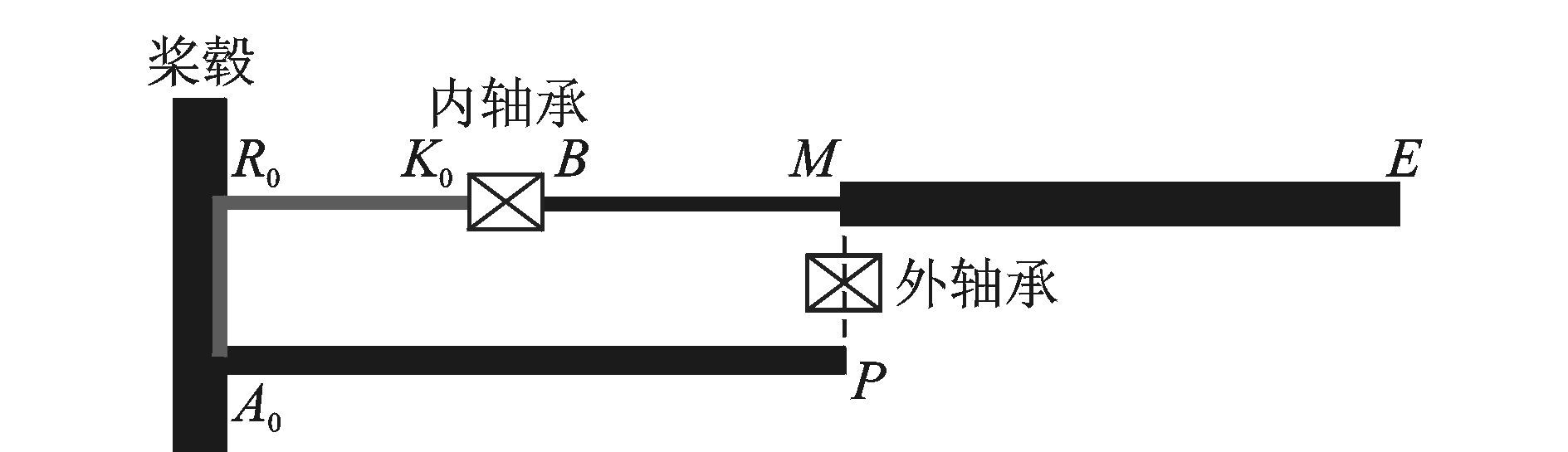
|
图 1 无铰式旋翼构型 Figure 1 Configuration of hingeless rotor |
图中A0P及BM为柔性梁,ME为桨叶翼型段,K0B为内轴承,MP为外轴承,其余部分则为刚体。基于连续体假设,柔性梁A0P的边界条件为
| $\left. \begin{align} & {{V}_{{{A}_{0}}}}-{{V}_{{{R}_{0}}{{A}_{0}}}}=0 \\ & {{\Omega }_{{{A}_{0}}}}-{{\Omega }_{{{R}_{0}}{{A}_{0}}}}=0 \\ \end{align} \right\}柔性梁{{A}_{0}}P根部$ | (8) |
以及
| $\left. \begin{align} & {{F}_{P}}-F_{MP}^{P}=0 \\ & {{M}_{P}}-M_{MP}^{P}=0 \\ \end{align} \right\}柔性梁{{A}_{0}}P根部$ | (9) |
柔性梁BM的左边界条件为
| $\left. \begin{align} & {{V}_{B}}-{{V}^{*}}=0 \\ & {{\Omega }_{B}}-{{\Omega }^{*}}=0 \\ \end{align} \right\}柔性梁BM根部$ | (10) |
式中:
为了描述柔性梁BM的左边界条件以及建立关于内轴承K0B的平衡方程,沿着3个坐标系(K0K轴垂直于内轴承中心轴线K0B指向上,K0B轴位于内轴承中心轴线上,Z0Z轴由右手坐标系确定)方向分别布置一组线弹簧和角弹簧,来模拟弹性内轴承里橡胶弹性材料沿3个方向的相对平移和转动,另外Z0Z方向的角弹簧还向桨叶提供变距角。内轴承处的力平衡条件为
| $\left\{ \begin{align} & {{F}_{{{K}_{0}}B}}-{{K}_{l{{K}_{0}}B}}{{U}_{{{K}_{0}}B}}-{{C}_{l{{K}_{0}}B}}{{{\dot{U}}}_{{{K}_{0}}}}B=0 \\ & {{M}_{{{K}_{0}}B}}-{{K}_{r{{K}_{0}}B}}{{\Theta }_{{{K}_{0}}B}}-{{C}_{r{{K}_{0}}B}}{{{\dot{\Theta }}}_{{{K}_{0}}B}}=0 \\ \end{align} \right.$ | (11) |
式中:KlK0B和ClK0B为内轴承K0B的线刚度和阻尼矩阵;KrK0B和CrK0B为内轴承K0B的角刚度和阻尼矩阵;FK0B和MK0B为柔性梁BM根部剖面B处的剪力和弯矩。
1.1.3 气动力模型本文的非定常动态失速模型结合了Leishman-Beddoes气动力模型与Peters动态入流模型,将所得模型代入旋翼气动弹性综合模型中,求解时用Peters动态入流模型计算诱导速度λ,用Leisman-Beddoes气动力模型求解气动载荷DBE(f,m)(包含升力、阻力及变距力矩),获得了分析综合方程(式(15) )的右端项,进而可求出桨叶的动响应,具体推导过程及形式参见文献[7]。
1.2 基于伽辽金法的变阶有限元离散格式采用正交勒让德多项式Φj(x)为试探函数,将第i
| $\left\{ \begin{align} & {{F}^{i}}({{x}^{i}},t)=\sum\limits_{j=0}^{m}{{{\Phi }^{j}}\left( {{{\bar{x}}}^{i}} \right){{f}^{j,i}}\left( t \right)} \\ & {{M}^{i}}({{x}^{i}},t)=\sum\limits_{j=0}^{m}{{{\Phi }^{j}}\left( {{{\bar{x}}}^{i}} \right){{m}^{j,i}}\left( t \right)} \\ & {{V}^{i}}({{x}^{i}},t)=\sum\limits_{j=0}^{m}{{{\Phi }^{j}}\left( {{{\bar{x}}}^{i}} \right){{v}^{j,i}}\left( t \right)} \\ & {{\Omega }^{i}}({{x}^{i}},t)=\sum\limits_{j=0}^{m}{{{\Phi }^{j}}\left( {{{\bar{x}}}^{i}} \right){{\Omega }^{j,i}}\left( t \right)} \\ \end{align} \right.$ | (12) |
式中:fj,i,mj,i,vj,i,ωj,i为桨叶变形后坐标系B中第i个单元、第j阶插值函数下3个方向上的变量。则第i个单元的有限元方程为
| $\begin{align} & \int_{0}^{{{L}^{i}}}{{{\Phi }^{k}}}\left[ \left( {{G}^{i}}\Phi {{~}^{j}}{{{\dot{v}}}^{j,i}}+\text{ }{{K}^{i}}\Phi {{~}^{j}}{{{\dot{\omega }}}^{j,i}} \right) \right.\text{ }~+ \\ & \widetilde{\text{ }\Phi {{~}^{p}}{{\omega }^{p,i}}}\left( {{G}^{i}}\Phi {{~}^{j}}{{v}^{j,i}}~+\text{ }{{K}^{i}}\Phi {{~}^{j}}{{\omega }^{j,i}} \right)-\Phi {{~}^{j}}^{\prime }{{f}^{j,i}}- \\ & \left( \widetilde{{{k}^{i}}}~+\text{ }\widetilde{{{S}^{i}}^{^{T}}\Phi {{~}^{p}}{{f}^{p,i}}}~+\text{ }\widetilde{{{T}^{i}}\Phi {{~}^{p}}{{m}^{p,i}}} \right)\Phi {{~}^{j}}{{f}^{j,i}}-\left. f{{~}^{i}} \right]d{{x}^{i}}~ \\ & +\text{ }\Phi {{~}^{k}}\left( 1 \right)\left[ \Phi {{~}^{j}}\left( 1 \right){{f}^{j,i}}-\Phi {{~}^{j}}\left( 0 \right){{f}^{j,i\text{ }+\text{ }1}}~ \right]=\text{ }0 \\ & \int_{0}^{{{L}^{i}}}{{{\Phi }^{k}}}\left[ \left( {{K}^{i}}^{^{T}}\Phi {{~}^{j}}{{{\dot{v}}}^{j,i}}+\text{ }{{I}^{i}}\Phi {{~}^{j}}{{{\dot{\omega }}}^{j,i}} \right) \right.~+ \\ & \text{ }\widetilde{\Phi {{~}^{p}}{{\omega }^{p,i}}}\left( {{K}^{i}}^{^{T}~}\Phi {{~}^{j}}{{v}^{j,i}}~+\text{ }{{I}^{i}}\Phi {{~}^{j}}{{\omega }^{j,i}}~ \right)+ \\ & \widetilde{\text{ }\Phi {{~}^{p}}{{v}^{p,i}}}\left( {{G}^{i}}\Phi {{~}^{j}}{{v}^{j,i}}~+\text{ }{{K}^{i}}\Phi {{~}^{j}}{{\omega }^{j,i}} \right)- \\ & \Phi {{~}^{j}}^{\prime }{{m}^{j,i}}-\left( \widetilde{{{k}^{i}}~}+\text{ }\widetilde{{{S}^{i}}^{T}\Phi {{~}^{p}}{{f}^{p,i}}}~+\widetilde{\text{ }{{T}^{i}}\Phi {{~}^{p}}{{m}^{p,i}}} \right)\Phi {{~}^{j}}{{m}^{j,i}} \\ & -\left( \widetilde{{{e}_{1~}}}+\text{ }\widetilde{{{R}^{i}}\Phi {{~}^{p}}{{f}^{p,i}}~}+\text{ }\widetilde{{{S}^{i}}\Phi {{~}^{p}}{{m}^{p,i}}} \right)\Phi {{~}^{j}}{{f}^{j,i}}-\left. m{{~}^{i}} \right]d{{x}^{i}}+ \\ & \Phi {{~}^{k}}\left( 1 \right)\left[ \Phi {{~}^{j}}\left( 1 \right){{m}^{j,i}}-\Phi {{~}^{j}}\left( 0 \right){{m}^{j,i\text{ }+\text{ }1}}~ \right]=\text{ }0 \\ & \int_{0}^{{{L}^{i}}}{{{\Phi }^{k}}}\left[ \left( {{R}^{i}}\Phi {{~}^{j}}{{{\dot{f}}}^{j,i}}~+\text{ }{{S}^{i}}\Phi {{~}^{j}}{{{\dot{m}}}^{j,i}} \right) \right.-\Phi {{~}^{j}}^{\prime }{{v}^{j,i}} \\ & -\left( \widetilde{{{k}^{i}}~}+\text{ }\widetilde{{{S}^{i}}^{T}\Phi {{~}^{p}}{{f}^{p,i}}}~+\text{ }\widetilde{{{T}^{i}}{{\Phi }^{p}}{{m}^{p,i}}} \right)\Phi {{~}^{j}}{{v}^{j,i}}- \\ & \left( \widetilde{{{e}_{1~}}}+\text{ }\widetilde{{{R}^{i}}\Phi {{~}^{p}}{{f}^{p,i}}}~+\text{ }\widetilde{{{S}^{i}}\Phi {{~}^{p}}{{m}^{p,i}}} \right)\left. \Phi {{~}^{j}}{{\omega }^{j,i}} \right]d{{x}^{i}} \\ & ~+\text{ }\Phi {{~}^{k}}\left( 0 \right)\left[ \Phi {{~}^{j}}\left( 1 \right){{v}^{j,i-1}}-\Phi {{~}^{j}}\left( 0 \right){{v}^{j,i}} \right]~=\text{ }0 \\ & \int_{0}^{{{L}^{i}}}{{{\Phi }^{k}}}\left[ \left( {{S}^{i}}^{T}\Phi {{~}^{j}}{{{\dot{f}}}^{j,i}}~+\text{ }{{T}^{i}}\Phi {{~}^{j}}{{{\dot{m}}}^{j,i}} \right) \right.-\Phi {{~}^{j}}^{'}{{w}^{j,i}} \\ & -\left( \widetilde{{{k}^{i}}~}+\text{ }\widetilde{{{S}^{i}}^{T}\Phi {{~}^{p}}{{f}^{p,i}}}+\text{ }\widetilde{{{T}^{i}}\Phi {{~}^{p}}{{m}^{p,i}}} \right)\Phi {{~}^{j}}{{w}^{j,i}}-\left. f{{~}^{i}} \right]d{{x}^{i}}+ \\ & \Phi {{~}^{k}}\left( 0 \right)\left[ \Phi {{~}^{j}}\left( 1 \right){{w}^{j,i-1}}-\Phi {{~}^{j}}\left( 0 \right){{w}^{j,i}} \right]~=\text{ }0 \\ \end{align}$ | (13) |
式中:Ri,Si,Ti为第i个单元剖面的柔度特性矩阵;Gi,Ki,Ii为第i个单元剖面的惯性特性矩阵;ki第i个单元的预扭/预弯分布;f i和mi为第i个单元的分布外载荷(载荷形式可以是重力、气动分布力等)。假设单元内剖面特性一致,提取出变量前面的积分项,令
| ${{q}^{i}}\left( t \right)=\left\{ {{\nu }^{0,i}}\left( t \right){{\omega }^{0,i}}\left( t \right){{f}^{0,i}}\left( t \right){{m}^{0,i}}\left( t \right)\cdots \right\}$ |
写成一阶状态空间方程
| ${{A}_{ji}}{{\dot{q}}_{i}}+{{B}_{ji}}{{q}_{i}}+{{C}_{jik}}{{q}_{i}}{{q}_{k}}+{{D}_{j}}=0$ | (14) |
针对一般无铰式旋翼构型,联立桨叶全本征动力学方程、无铰式旋翼内轴承平衡方程,动态入流方程,得到无铰式旋翼气动弹性综合模型,混合状态空间方程为
| $\eqalign{ & \left[ {\matrix{ { - {C_{{K_0}B}}} & 0 & 0 \cr 0 & {{A_{BE}}} & 0 \cr 0 & 0 & M \cr } } \right]\left[ {\matrix{ {{{\dot q}_{{K_0}B}}} \cr {{{\dot q}_{BE}}} \cr {\dot \lambda } \cr } } \right] + \cr & \left[ {\matrix{ { - {K_{{K_0}B}}} & 0 & 0 \cr 0 & {{B_{BE}} + C\left( {{q_{BE}}} \right)} & 0 \cr 0 & 0 & {{{\hat L}^{ - 1}}} \cr } } \right]\left[ {\matrix{ {{{\dot q}_{{K_0}B}}} \cr {{{\dot q}_{BE}}} \cr {\dot \lambda } \cr } } \right] = \cr & \left[ {\matrix{ { - {D_{{K_0}B}}\left( {q_{BE}^{0,1}} \right)} \cr { - {D_{BE}}\left( {f,m} \right)} \cr 0 \cr } } \right] \cr} $ | (15) |
式中:qK0B为无铰式旋翼内轴承K0B的自由度;qBE为柔性桨叶段的自由度;λ为诱导入流自由度;DBE(f,m)=DBE(fG,mG)+DBE(faero,maero),包含重力和气动载荷对结构的贡献。
2 旋翼气弹响应稳态周期解的计算与稳定性分析方法 2.1 旋翼气动/动力学耦合分析方法本文采用旋翼动力学/气动力紧耦合求解方法,分为内外两层迭代过程,如图 2所示。外层迭代为配平,其求解采用Newton-Raphson方法,并用刚性桨叶的分析结果作为求解过程的初值。内层迭代为旋翼气弹响应稳态周期解的计算,具体计算步骤为:
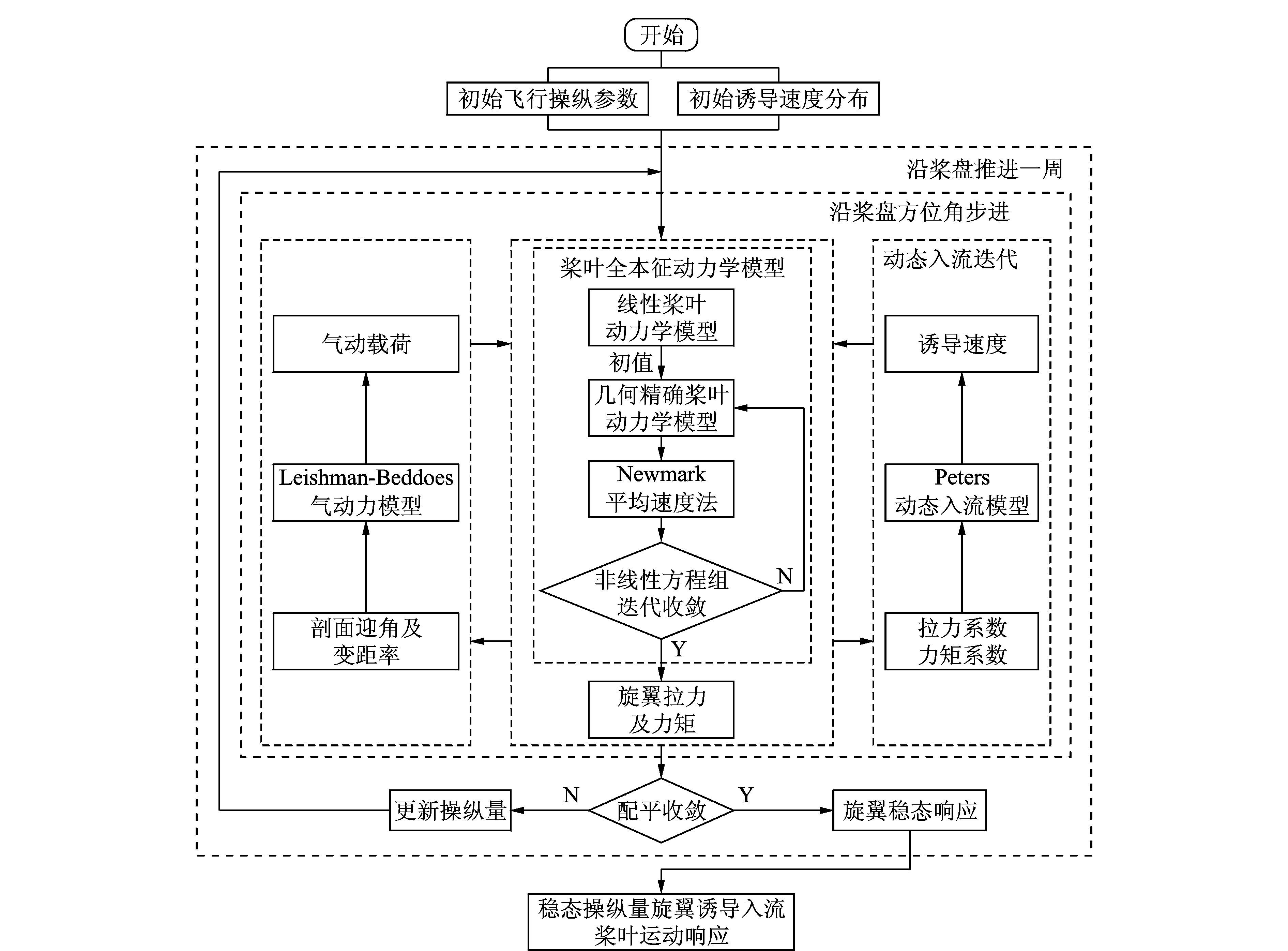
|
图 2 旋翼气动/动力学耦合分析流程 Figure 2 Flow chart of rotor dynamics and airdynamics coupling analysis |
(1) 根据给定状态的飞行操纵参数,估算出桨盘诱导速度分布的初始值。
(2) 沿桨盘方位角步进,调用桨叶全本征动力学模型及Leishman-Beddoes非定常动态失速模型,采用Newmark平均速度法计算旋翼桨叶动力学响应(响应自由度包含线速度V、角速度Ω、剖面力F及剖面力矩M)。
(3) 根据求得的动力学响应,合成旋翼拉力系数和力矩系数,再调用动态入流模型求出旋翼诱导入流沿桨盘的分布,进而及时更新方程中气动力相关项,这也是耦合策略“紧”的体现。
(4) 同一时刻内,判断各片桨叶响应的残差值和旋翼入流的残差值是否满足当前步给定的收敛标准,如不满足精度要求,循环执行步骤(2,3) ,当满足精度要求时,沿方位角前进一步。
(5) 沿桨盘方位角步进一周,利用配平模型更新旋翼操纵量,判断旋翼操纵量的残差值是否满足给定配平收敛标准,当满足精度要求时,旋翼气动/动力学耦合模型求解过程结束。
2.2 旋翼气动弹性稳定性分析方法目前直升机旋翼气动弹性稳定性分析方法有两种:(1) 通过求出的旋翼稳态周期解,在其附近扰动得到线化的增量方程,通过增量方程的特征值得到旋翼稳定性分析结果,比较常用的有常系数假设法和Floquet理论;(2) 本文将着重介绍和使用的“瞬态响应分析法”[9]。
图 3为旋翼气动弹性稳定性分析流程图。图 3(a)所示的实验[10]过程中,通过伺服液压控制器控制液压作动筒对自动倾斜器不旋转环施加周期激励,传到自动倾斜器旋转环上的频率为旋翼转速频率加减激励频率,周期激振力通过与旋转环相连的操纵拉杆对桨叶的桨距角施加同频的周期激励,通过角位移传感器采集到的摆振衰减运动响应交给动态数据采集系统,最后利用移动矩形窗法识别系统阻尼并分析系统气动弹性稳定性。图 3(b)所示的数值模拟流程,即“瞬态响应分析法”过程。
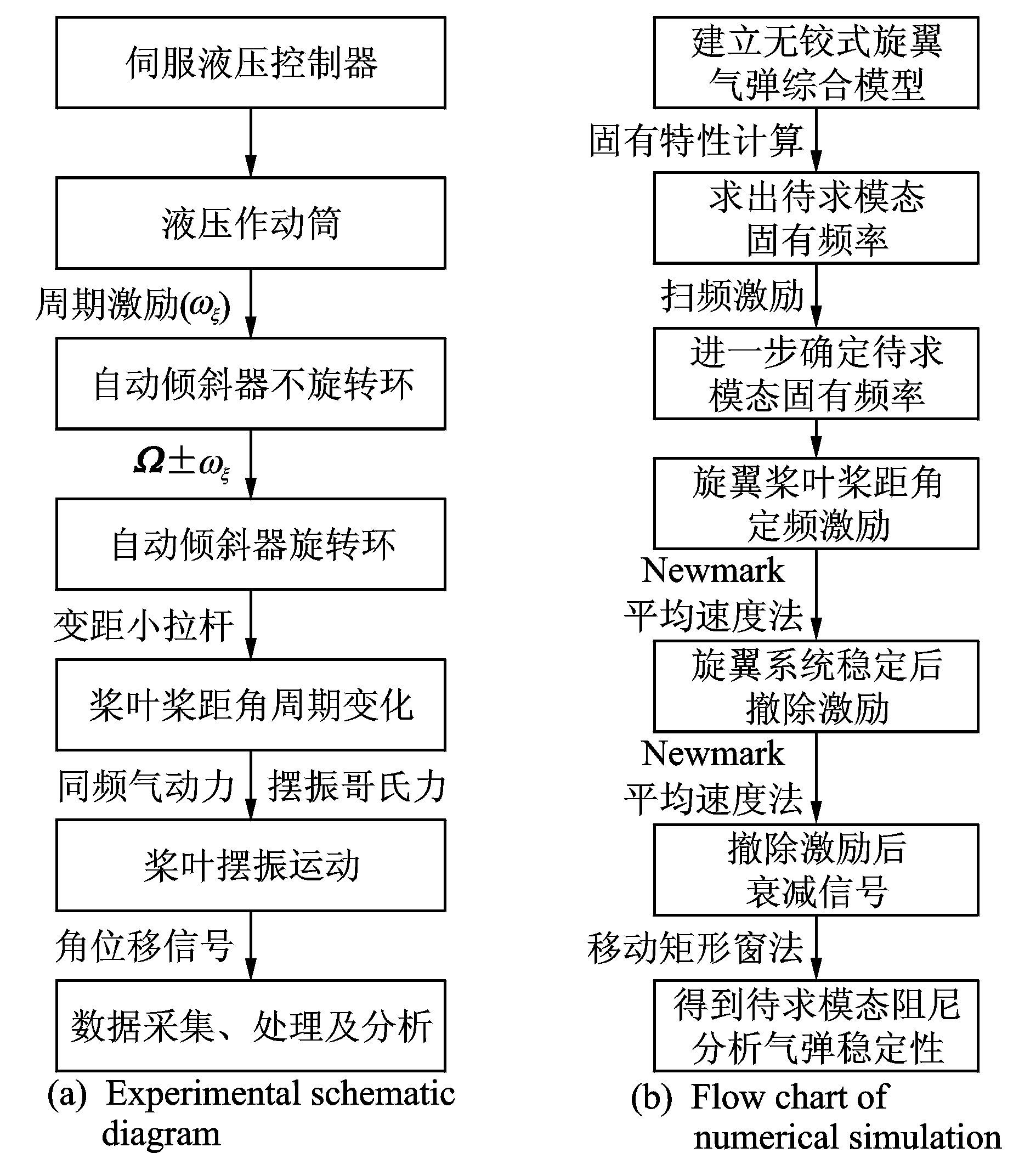
|
图 3 旋翼气动弹性稳定性分析流程 Figure 3 Analysis process of rotor aeroelasticity |
3 算例验证 3.1 新型无铰式旋翼根部多路传力区边界条件验证
为了验证本文动力学模型中这种边界处理方法的有效性,选取文献[8]中的结构参数,并与直升机多体动力学分析软件DYMORE计算值进行了对比验证。
图 4给出了无铰式旋翼构型在其自重作用和旋转影响下的轴向力、剪力及挥舞弯矩分布,同时还给出了该构型的DYMORE计算值。通过对比看出,本文所建立的新型无铰式旋翼边界条件能够准确满足多路传力区的载荷平衡关系。
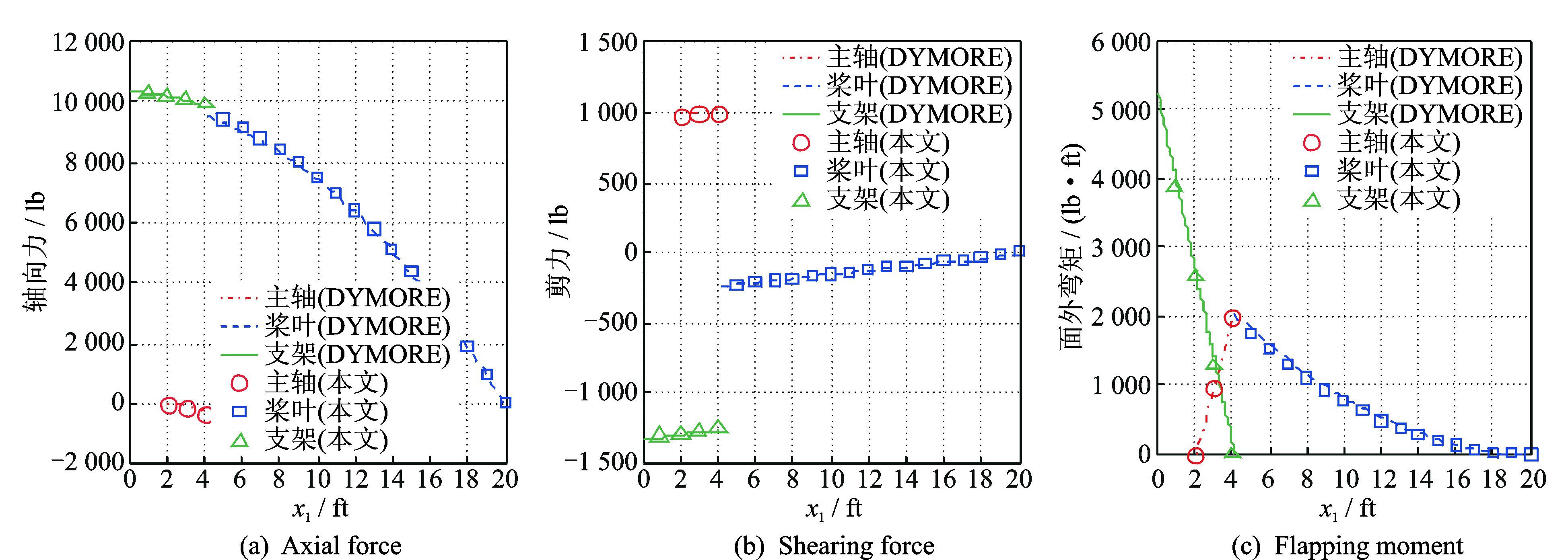
|
图 4 无铰式旋翼桨叶剖面载荷 Figure 4 Section load of hingless rotor blade |
3.2 BO105旋翼气弹响应与振动载荷分析验证
本文采用文献[11] BO105中速前飞状态验证无铰式旋翼气动弹性综合分析模型。BO105旋翼桨毂偏置处只安装有变距铰,4片桨叶翼型均为NACA23012。本文配平参数见表 1。与文献[11]计算结果相比差异较小,精度较高。略有差异的原因主要有两点:(1) 文献[11]中的配平为考虑旋翼、机身和尾翼的全机配平模型,本文采用的是孤立旋翼配平模型;(2) 文献[11]中采用的气动力模型仅为线性定常气动力模型,目的仅是为了验证UMARC软件更新程序的正确性。
| 表 1 BO105中速前飞状态参数 Table 1 State parameters at moderate speed of BO105 |
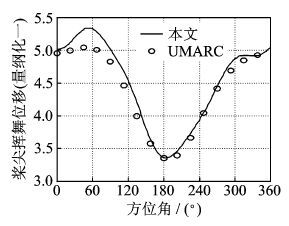
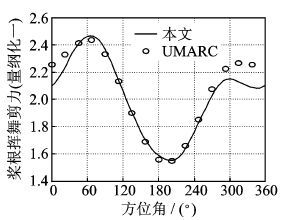
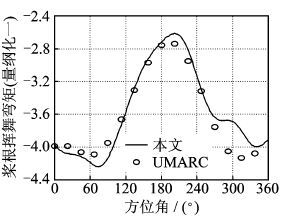
图 5~7分别将桨尖挥舞位移、桨根挥舞剪力和挥舞弯矩的本文计算值与直升机动力学综合分析软件UMARC [11]中给出的结果进行对比,可以看出本文计算值的整体变化趋势与UMARC给出的结果基本一致。一阶谐波在图 5~7中周向分布位置与UMARC中给出的结果吻合程度较好,相位计算精度较高。但是,由于本文在气动力方面耦合采用非定常气动力模型,在270°方位角附近桨根挥舞载荷中呈现出一些高阶谐波成分,使得在270°方位角附近本文计算值与UMARC计算结果在幅值上产生了差异。
|
图 5 桨尖挥舞位移 Figure 5 Flapping displacement of blade tip |
|
图 6 桨根挥舞剪力 Figure 6 Flapping shear of blade root |
|
图 7 桨根挥舞弯矩 Figure 7 Flapping moment of blade root |
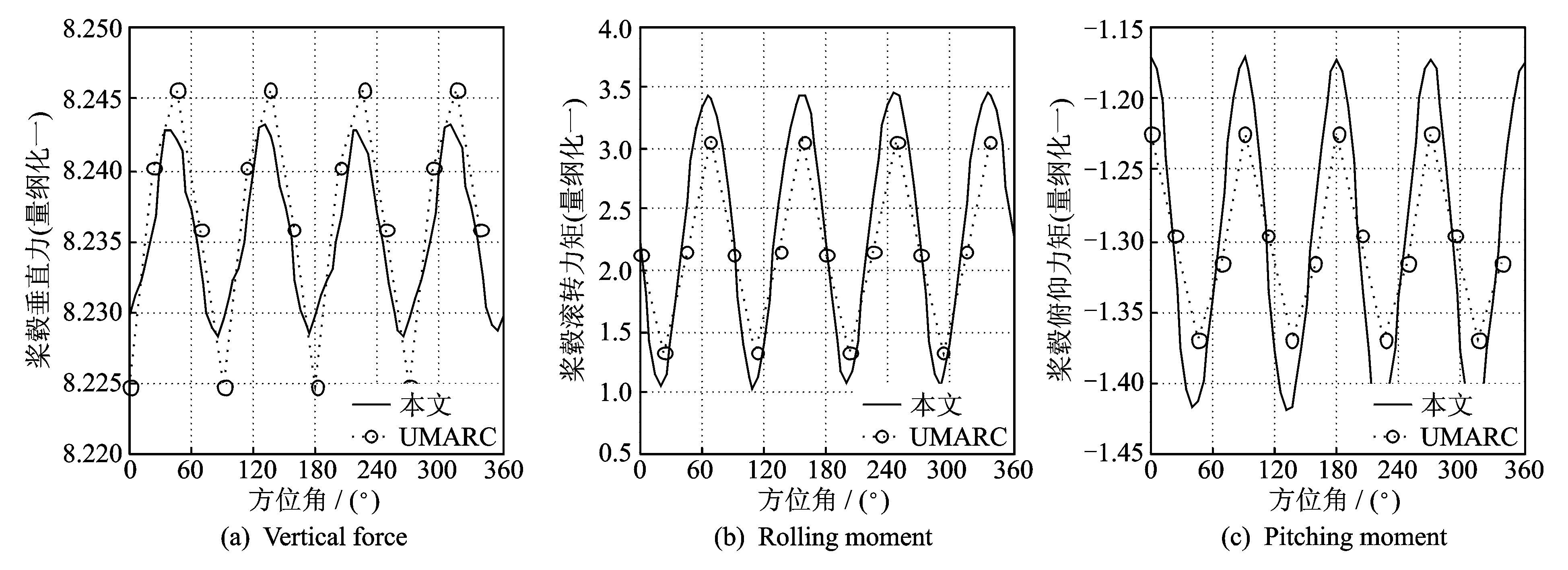
图 8对比验证了桨毂载荷本文计算值与UMARC[11]中给出的结果。可以看出本文桨毂载荷计算均值、整体变化趋势与UMARC给出的结果呈现出一致性,峰峰值略有差异(UMARC通过全机配平模型得到配平后操纵量,进行桨毂载荷计算;本文只进行孤立旋翼配平,没有考虑机体和桨毂载荷之间的耦合影响)。四阶谐波在图 8中周向分布位置与UMARC中给出的结果吻合程度较好,相位计算精度较高。
|
图 8 旋翼桨毂载荷 Figure 8 Rotor hub load |
3.3 无铰式旋翼悬停气动弹性稳定性分析验证
本文采用美国陆军航空飞行管理局用于检验无铰式旋翼气弹稳定性分析精度而研制的标准模型桨叶,验证本文无铰式旋翼气动弹性稳定性计算分析精度。旋翼桨叶分为0°,2°预锥角两种安装方式。
采用“瞬态响应分析法”分析悬停气动弹性稳定性,分别得到如图 9所示的0°,2°预锥角下的摆振阻尼随总距角变化曲线。由图 9可知,本文计算结果和文献[12]中给出的试验值变化趋势一致,小总距时摆振模态阻尼的理论计算值与试验值吻合较好,大总距时的差异主要是由于模型旋翼桨叶在风洞中做试验时产生的回流及地效的影响,致使试验值有较大的分散性。此例验证了本文建立的无铰式旋翼气动弹性综合模型及稳定性分析方法在悬停气动弹性稳定性分析中的正确性。
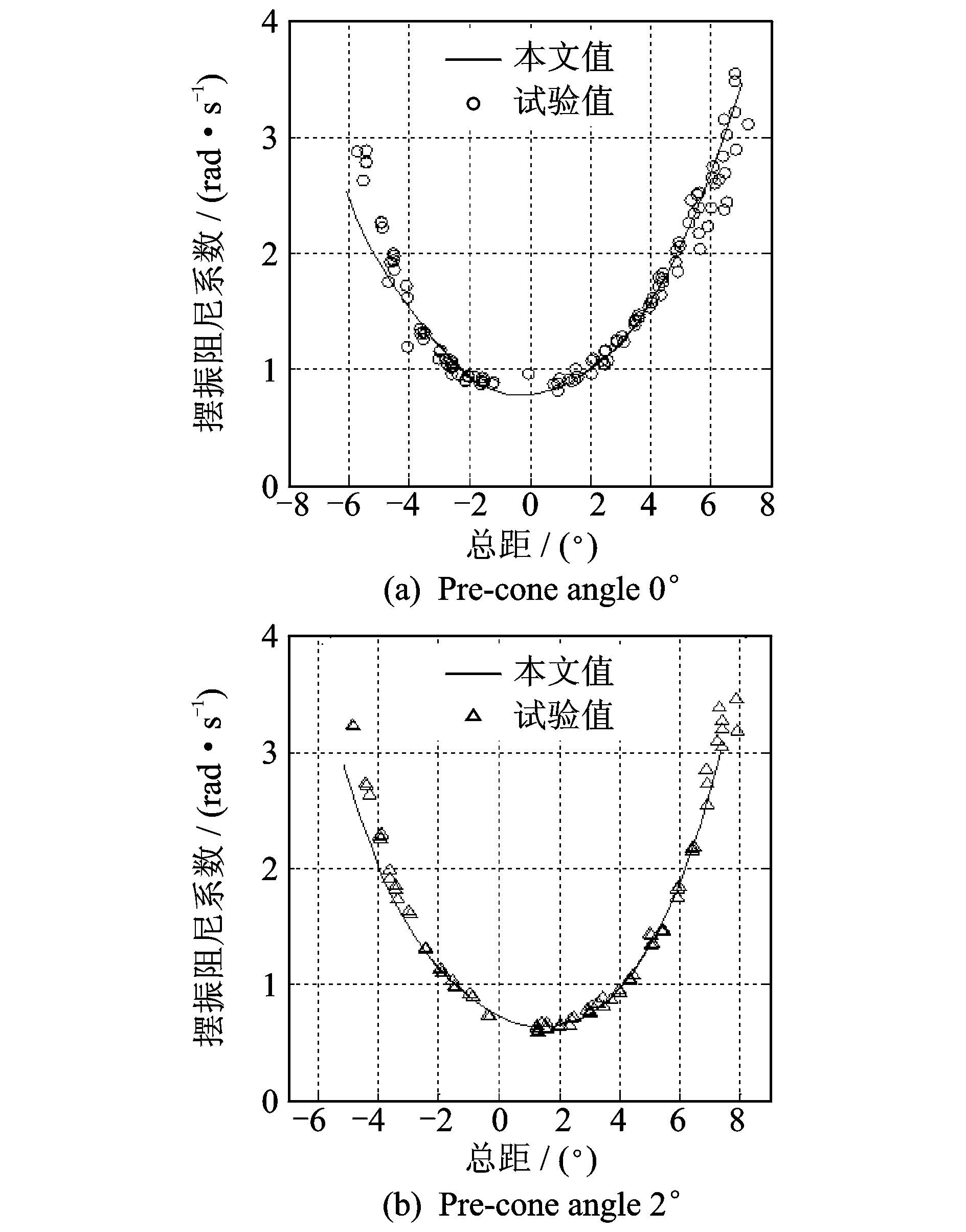
|
图 9 悬停状态摆振阻尼随总距角的变化曲线 Figure 9 Lag damper changing with collective pitch at hover state |
4 结束语
本文建立了适合于新型无铰式旋翼气弹综合分析的全本征动力学模型,构造了基于伽辽金法的变阶有限单元,采用牛顿松弛迭代和Newmark平均速度法求解无铰式旋翼气弹方程。算例对比表明,该模型能准确模拟新型无铰式旋翼根部多路传力区的载荷平衡关系,气弹响应、载荷及稳定性求解精度较高,具有一定的工程实用价值。
| [1] | Hodges D H, Dowell E H. Nonlinear equation of motion for the elastic bending and torsion of twisted nonuniform rotor blades[R]. NASA TN D-7818,1974. |
| [2] | Hodges D H. A mixed variational formulation based on exact intrinsic equations for dynamics of moving beams[J]. International Journal of Solids and Structures , 1990, 26 (11) : 1253–1273. DOI:10.1016/0020-7683(90)90060-9 |
| [3] | Hodges D H. Nonlinear composite beam theory[M]. Virginia: AIAA, 2006 : 262 -269. |
| [4] | Peters D A. How dynamic inflow survives in the competitive world of rotorcraft aerodynamics[J]. Journal of the American Helicopter Society , 2009, 54 (1) : 11001–1. DOI:10.4050/JAHS.54.011001 |
| [5] | Leishman J. Validation of approximate indicial aerodynamic functions for two-dimensional subsonic flow[J]. Journal of Aircraft , 1988, 25 (10) : 914–922. DOI:10.2514/3.45680 |
| [6] | Beddoes T. Practical computation of unsteady lift[J]. Vertica , 1984, 8 (1) : 55–71. |
| [7] |
王博. 基于全本征方程的无铰式旋翼气动弹性分析方法[D]. 南京: 南京航空航天大学, 2015. Wang Bo. Analytical method on aeroelasticity of hingeless rotor using fully intrinsic equations[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. |
| [8] | Sotoudeh Z, Hodges D H. Structural dynamics analysis of rotating blades using fully intrinsic equations, Part II: Dual-load-path configurations[J]. Journal of the American Helicopter Society , 2013, 58 (3) : 1–9. |
| [9] |
虞志浩, 杨卫东, 邓景辉, 等.
基于多体动力学的旋翼模型与气弹稳定性[J]. 航空动力学报 , 2012, 27 (5) : 1122–1130.
Yu Zhihao, Yang Weidong, Deng Jinghui, et al. Model of rotor aeroelastic stability using dynamics of flexible multibody systems[J]. Journal of Aerospace Power , 2012, 27 (5) : 1122–1130. |
| [10] |
杨卫东, 马杰, 张呈林.
带粘弹减摆器旋翼系统气弹稳定性试验与阻尼识别[J]. 振动工程学报 , 2007, 20 (1) : 101–106.
Yang Weidong, Ma Jie, Zhang Chenglin. Model experiment and damping identification for aeroelastic stability of helicopter rotor with elastomeric lag damper[J]. Journal of Vibration Engineering , 2007, 20 (1) : 101–106. |
| [11] | Bir G, Chopra I. University of Maryland advanced rotorcraft code (UMARC) theory manual [R]. UM-Aero Report, 92-02, 1992. |
| [12] | Maier T H, Sharpe D L. Fundamental investigation of hingless rotor aeroelastic stability[C]//Proceeding of 51th Annual Forum of the American Helicopter Society. Washington D C: AHS, 1995: 1176-1190. |
 2016, Vol. 48
2016, Vol. 48


