直升机在执行任务时可能会遇到恶劣天气,特别是在海面上执行任务时,复杂多变的海况会影响旋翼的起动和停转。直升机旋翼在起动和停转过程中,会以较低转速旋转,桨叶此时产生的离心力较小,导致桨叶的离心力刚度也较小。那么直升机在恶劣的环境下起动和停转时,桨叶的动响应将会受到很大的影响,桨尖就可能会产生过大的位移并与机身发生碰撞,在此过程中桨叶会与限动块发生较为强烈的碰撞。为了更好地描述桨叶与挥舞限动块之间的碰撞动响应,有必要更为深入地研究两者的碰撞动力学问题。
国内外已有多位学者对桨叶扬起下坠碰撞问题做了较为深入和细致的动力学研究。美国宾州州立大学的Keller教授和Smith教授对直升机桨叶下坠碰撞做了理论分析和试验研究[1-2],其理论模型中使用条件刚度扭转弹簧模拟桨叶与限动块之间的碰撞,当桨叶与限动块未接触时,扭转弹簧刚度设为0;当桨叶与限动块间发生或已经接触时,因为挥舞铰此时能够转动的角度很小,所以将扭转弹簧的刚度设定为一个较大值。英国南安普敦大学Newman教授针对直升机的“blade sailing”现象做了风洞测试[3],试验表明了直升机在舰面上的放置位置对桨叶的动响应有明显的影响。Geyer等对直升机旋翼在舰面上起动和停转过程中的气弹动力学问题做了研究[4],使用条件扭转弹簧来模拟桨叶与限动块之间的碰撞。Kang等分析了直升机旋翼在舰面上起动和停转问题[5],使用非线性弹簧模拟桨叶与限动块之间的碰撞。Bottasso和Bauchau对直升机旋翼在起动和停转过程中桨叶与限动块间的碰撞做了分析[6],将它们之间的碰撞力使用弹性力和耗散力的合力表示。加拿大卡尔顿大学Wall等构建了一个船-直升机-旋翼模型[7-8],该模型由多个离散的刚体和柔性体组成,用线性弹簧代替桨叶与限动块之间的碰撞。Khouli等综合模拟了直升机旋翼在舰面上的起动和停转[9-10],研究结果表明:该系统能够有效降低桨尖产生的过大位移及惯性载荷。Han等建立了一个能够描述舰载直升机旋翼起动和停转的系统[11],并运用桨叶扬起下坠试验验证了所建立模型的有效性。康浩等建立了舰载直升机旋翼在起动和停转过程中的瞬态气弹动力学分析模型[12],当桨叶与限动装置接触时,扭簧刚度取足够大的值;当桨叶不与限动装置接触时,扭簧刚度取为零。韩东等对直升机旋翼起动和停转过程中桨叶动响应做了研究[13-14],在对桨叶下坠碰撞过程研究时,使用条件弹簧模拟限动块间的碰撞。
在以往桨叶扬起下坠碰撞动力学研究中,通常使用线性或非线性条件扭转弹簧描述桨叶与限动块之间的碰撞过程。为了更好地描述桨叶扬起下坠动力学过程,本文运用含阻尼项的简化碰撞模型来模拟桨叶与限动块之间的碰撞,并对比分析扭转弹簧刚度、阻尼比和积分步长等对桨叶与挥舞限动块之间碰撞力矩的影响。
1 碰撞模型在不考虑空气动力的情况下,铰接式旋翼桨叶的扬起下坠运动仅会受自身重力的影响。桨叶绕挥舞铰做扬起下坠运动时,会与限动块发生碰撞。由于桨叶与限动块在碰撞前的相对速度较大,这就会造成初次碰撞时有较大的冲击力存在,当然也可能会有能量损耗。为了描述挥舞铰处碰撞力矩的变化,本文采用含阻尼项碰撞模型来模拟桨叶与限动块间的碰撞。碰撞模型由两部分组成,分别为条件扭转弹簧和阻尼。由于在碰撞过程中桨叶转动的角度较小,所以将条件扭转弹簧的刚度取较大值。阻尼是为了反映碰撞过程中的能量损耗。
1.1 刚度项根据桨叶是否与限动块发生碰撞,本文将模型分为两种状态,即未碰撞状态和碰撞状态。未碰撞状态时,桨叶与限动块之间没有接触,即接触力为0,此时扭转弹簧的刚度值取为0。碰撞状态时,桨叶与限动块之间已经接触或处于临界接触状态,此时扭转弹簧就处于工作状态,将其刚度值取为常值k。综上,刚度项kβ表达式为
| ${k_\beta } = \left\{ {\matrix{ 0 & {{\beta _h} > {\beta _D}} \cr k & {{\rm{ }}{\beta _h} \le {\beta _D}} \cr } } \right.$ | (1) |
式中:βh为挥舞角度;βD为挥舞限动角。
1.2 阻尼项在桨叶与限动块碰撞过程中,限动块会经历两种过程,即压缩过程和恢复过程。压缩过程中,桨叶与限动块间会保持两接触面相互贴合,并且在此过程中接触面间的相互作用力会不断地增大。恢复过程中,桨叶与限动块间不一定能够完全保证两接触面处于贴合状态,并且接触面间的作用力在不断地减小。根据上述特点,本文仅在压缩过程中应用阻尼,以模拟碰撞过程中的能量损耗。综上,阻尼项Cβ表达式为
| ${C_\beta } = \left\{ {\matrix{ {2\xi \sqrt {{I_\beta }{k_\beta }} } & {{\beta _h} \le {\beta _D}且{{\dot \beta }_h} \le 0} \cr 0 & {其他} \cr } } \right.$ | (2) |
式中:ξ为阻尼比;Iβ为挥舞铰外侧桨叶对挥舞铰的转动惯量;kβ为扭转弹簧刚度;
压缩过程中,碰撞力矩中包含扭转弹簧弹性力矩和阻尼力矩。恢复过程中,碰撞力矩中仅包含扭转弹簧弹力矩。综上,碰撞力矩Mβ表达式为
| ${M_\beta } = \left\{ {\matrix{ {{k_\beta }\left( {{\beta _h} - {\beta _D}} \right) + {C_\beta }{{\dot \beta }_h}} & {{{\dot \beta }_h} \le 0} \cr {{k_\beta }\left( {{\beta _h} - {\beta _D}} \right)} & {{{\dot \beta }_h} > 0} \cr } } \right.$ | (3) |
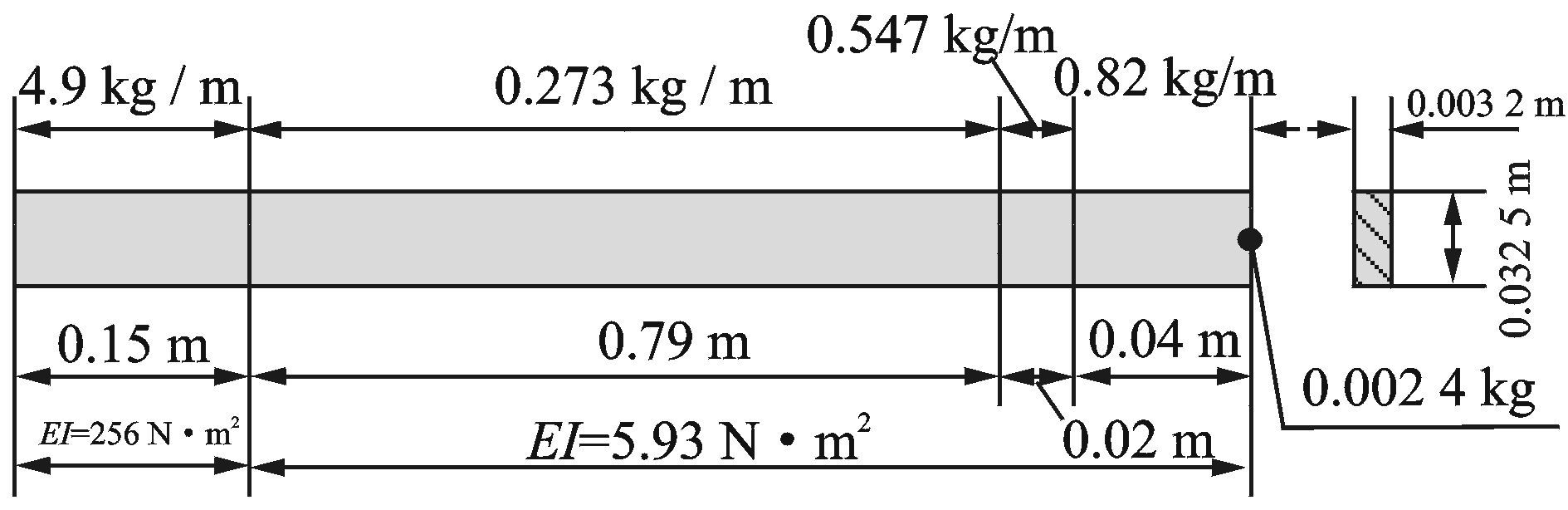
为验证碰撞模型的有效性,建立模型桨叶计算其扬起下坠动响应。该模型桨叶结构参数如下:横截面厚度h为0.003 2 m,长度L为1 m,弗洛德数Fr为0.181,挥舞限动角βD为0°,挥舞刚度EI分布和质量ρA(A为横截面面积)分布如图 1所示。
|
图 1 模型桨叶参数 Figure 1 Parameters of blade model |
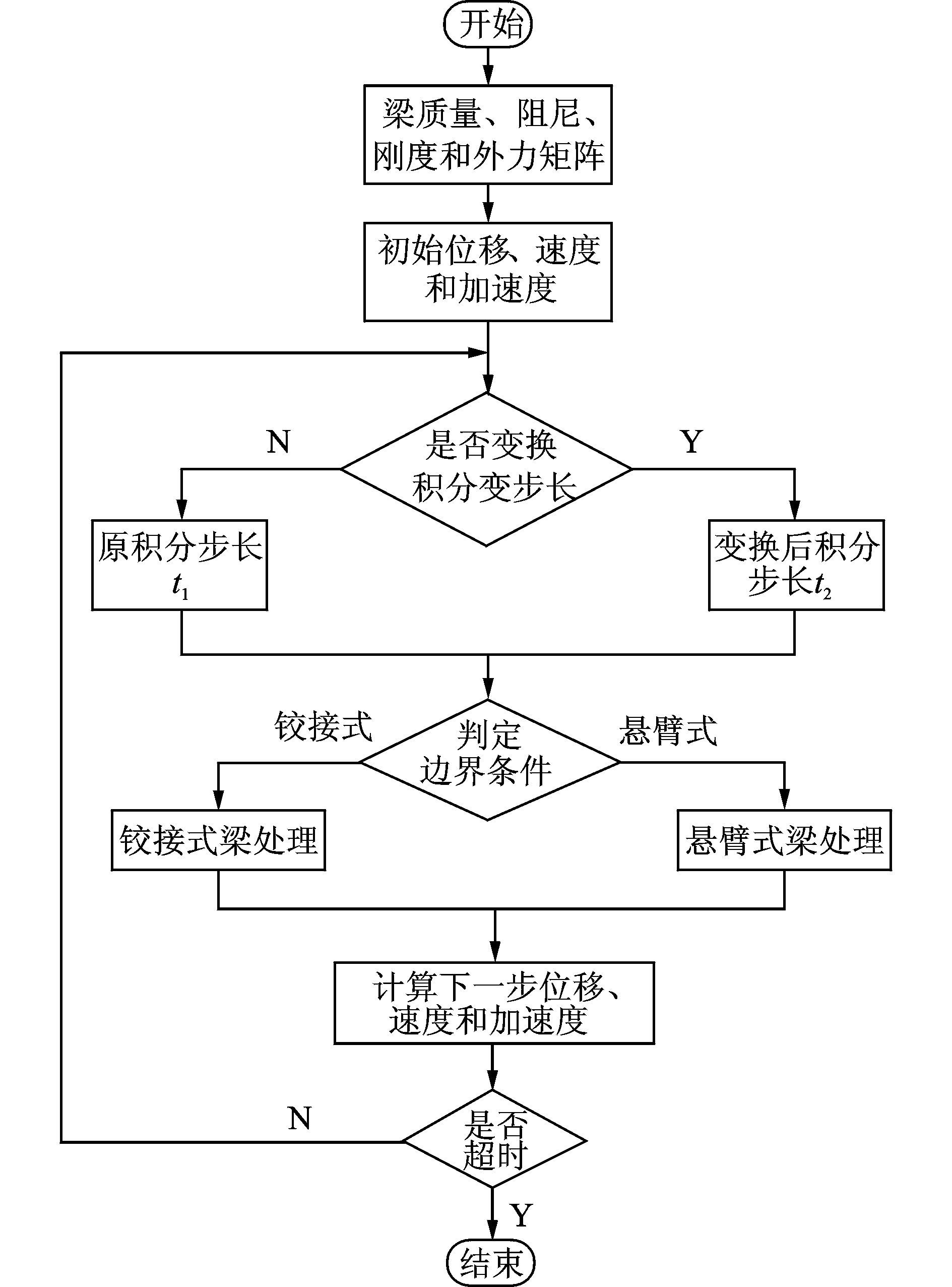
根据Hamilton原理建立桨叶扬起下坠动力学方程,将模型桨叶沿展长方向离散为20个梁单元,每个单元具有4个自由度,每个节点处包含两个自由度,分别为挥舞方向的挠度和转角。将桨叶绕挥舞铰自由转动时的状态称为铰接式模式(βh>βD),将桨叶与限动块发生碰撞后且并未分离时的状态称为悬臂式模式(βh≤βD)。桨叶从一初始角度处做扬起下坠运动时,运用Newmark积分法求解此运动过程中桨叶的动响应,其计算流程如图 2所示。
|
图 2 计算流程图 Figure 2 Calculation flowchart |
2.2 桨叶动响应分析
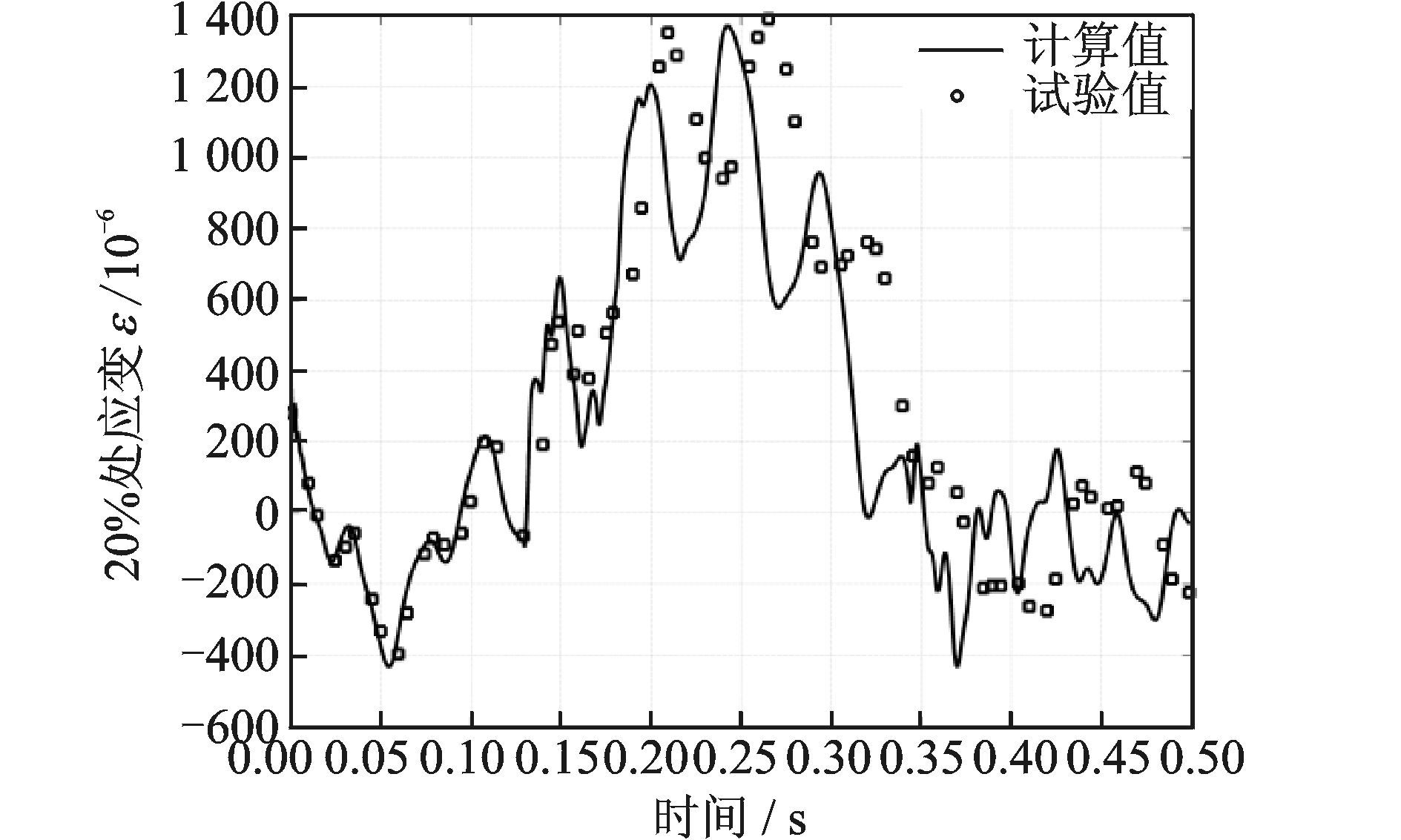
桨叶从初始角度为9.7°处开始做扬起下坠运动,其桨尖位移、挥舞角度、20%处表面应变随时间变化历程如图 3~5所示。桨尖位移的计算值与文献[1, 2]的试验值吻合较好,其最大位移误差为-2.13%,最大位移处时间误差为7.14%。对比挥舞角度变化情况可以发现,计算值与试验值吻合较好,但是在响应时间上有所超前。对比桨叶20%处应变随时间变化历程可以看出,最大应变误差为-1.37%。

|
图 3 桨尖位移随时间变化历程 Figure 3 Time history of tip deflection |

|
图 4 挥舞角度随时间变化历程 Figure 4 Time history of flap hinge angle |
|
图 5 桨叶20%处的应变随时间变化历程 Figure 5 Time history of strain at 20% of blade model |
2.3 刚度对碰撞力矩的影响
将碰撞模型中的扭转弹簧刚度k分别设置为1×103,1×104,1×105和1×106 N·m/rad,并将阻尼比和积分步长设置为相同值。在计算动响应过程中发现,扭转弹簧的刚度较大时,积分步长的大小对碰撞力矩是否收敛有很大影响。为了能够得到刚度为1×106 N·m/rad时的稳定解,将阻尼比取为0.03,积分步长取为1×10-6 s。
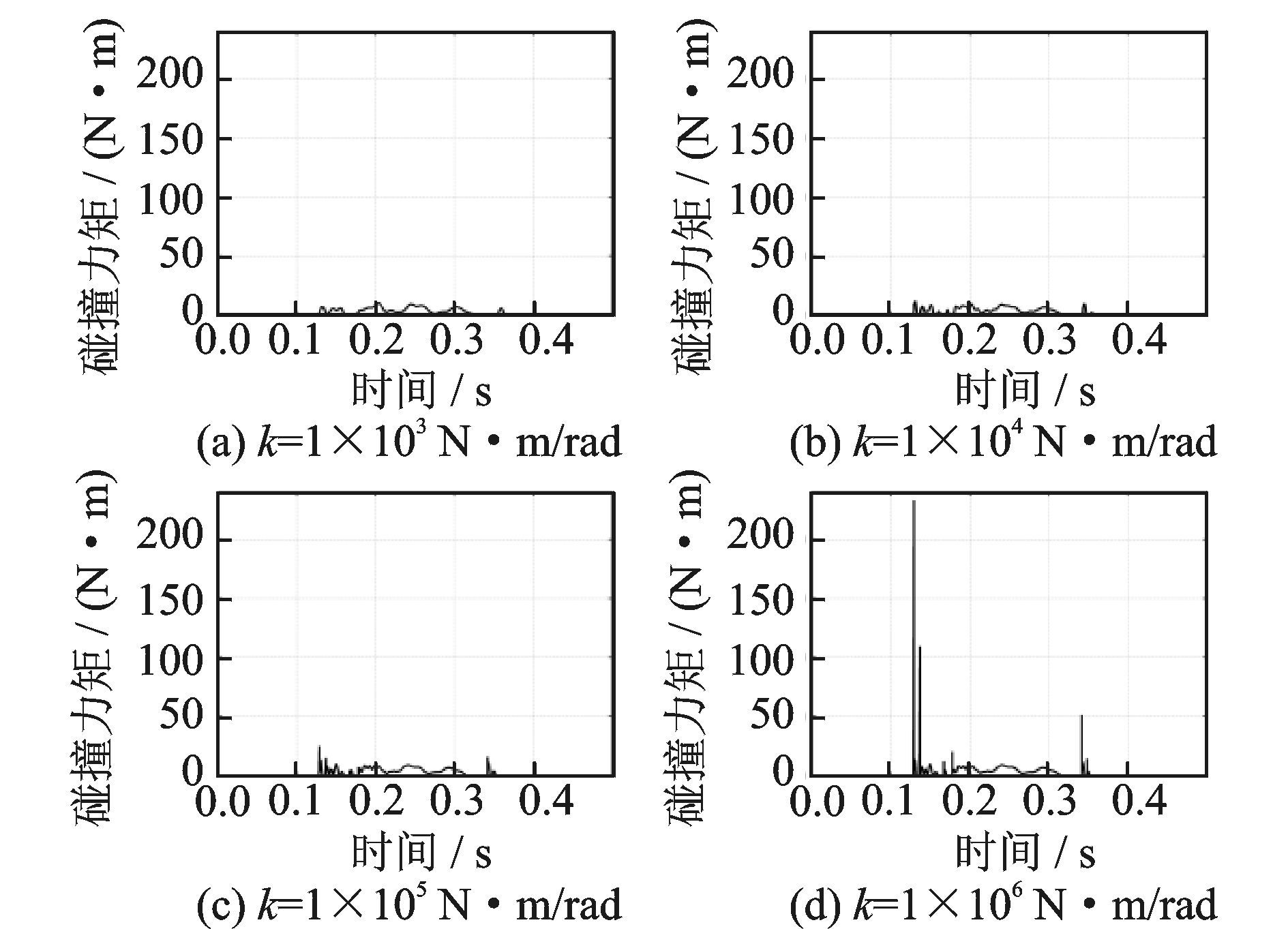
分别求解4种不同扭转弹簧刚度时桨叶的扬起下坠动响应,计算得到不同弹簧刚度时碰撞力矩随时间的变化曲线,如图 6所示。计算结果表明,随着扭转弹簧刚度的增大,碰撞力矩的峰值也随之增大。当扭转弹簧刚度由1×103 N·m/rad增加到1×106 N·m/rad时,计算得到的碰撞力矩峰值由10.2 N·m增加到233.2 N·m,增大了22.0倍,说明扭转弹簧刚度对碰撞力矩峰值影响较大。
|
图 6 不同弹簧刚度对碰撞力矩的影响 Figure 6 Contact moment changing with time under different spring stiffness |
2.4 阻尼比对碰撞力矩的影响
将碰撞模型中的阻尼比ξ分别设置为0,0.01,0.02,0.03,0.04和0.05,并将扭转弹簧刚度取为1×105 N·m/rad,积分步长设置为1×10-5 s。
分别求解6种不同阻尼比时桨叶的扬起下坠动响应,计算得到不同阻尼比时碰撞力矩随时间的变化曲线,如图 7所示。对比6种不同阻尼比计算得到的碰撞力矩图后发现,随着阻尼比的增大,碰撞力矩的峰值也随之增大。当阻尼比由0增加到0.05时,碰撞力矩的峰值由25.1 N·m增加到27.7 N·m,增加了10.4%,幅值增加相对较小,说明阻尼对碰撞力矩峰值影响相对较小。

|
图 7 不同阻尼比对碰撞力矩的影响 Figure 7 Contact moment changing with time under different damping ratios |
2.5 积分步长对碰撞力矩的影响
将积分步长分别设置为1×10-3,1×10-4,1×10-5和1×10-6 s,并将扭转弹簧刚度取为1×105 N·m/rad,阻尼比设置为0.03。
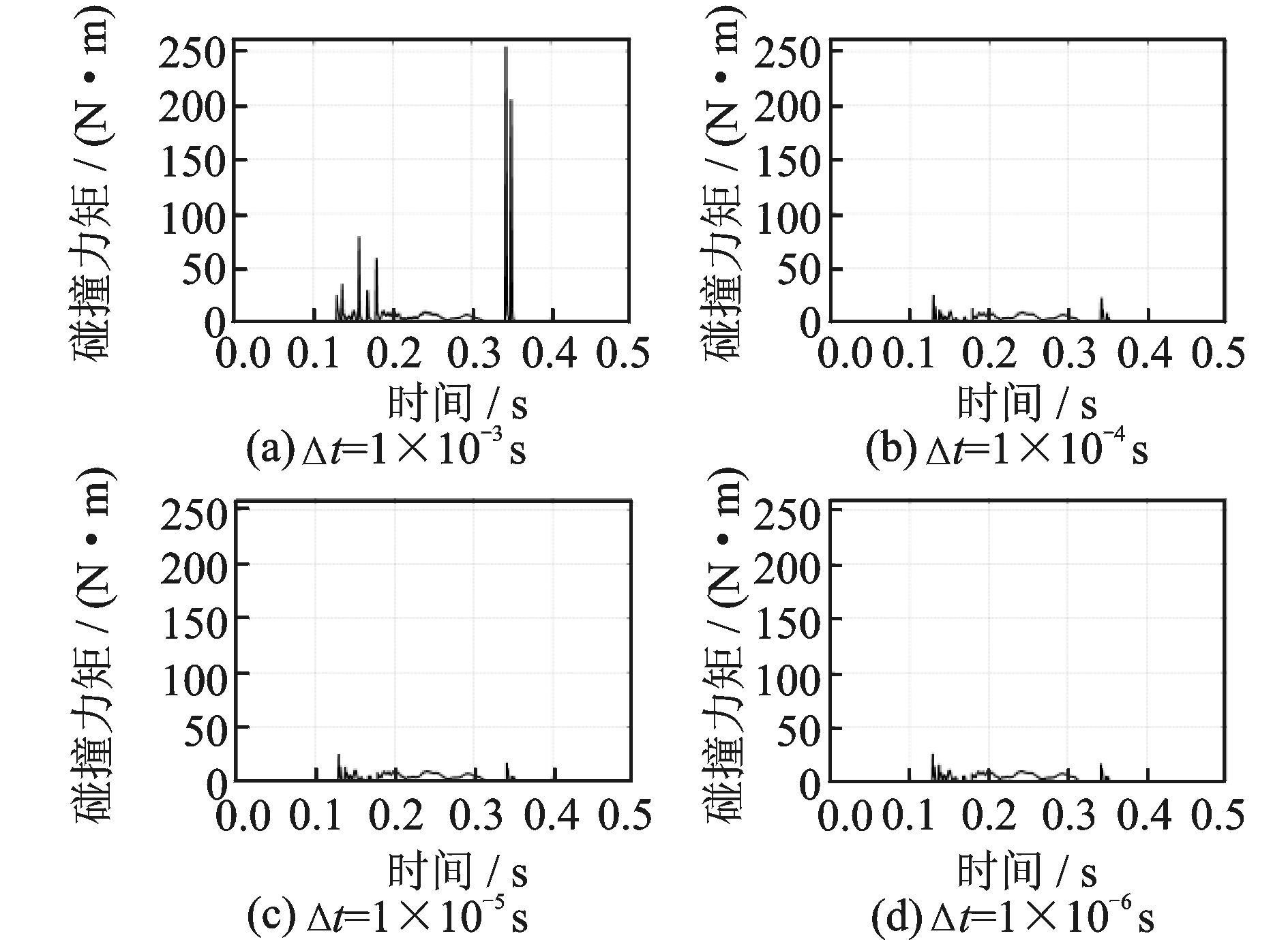
分别求解4种不同积分步长(Δt)时桨叶扬起下坠动响应,计算得到了不同积分步长时碰撞力矩随时间的变化曲线,如图 8所示。计算结果表明,随着积分步长的增大,计算得到的碰撞力矩峰值随之减小,最后趋于稳定。当积分步长为1×10-3 s时,碰撞力矩随时间变化曲线存在突变,说明此步长时的计算结果收敛性较差。当积分步长小于1×10-4 s时,计算结果收敛性较好,但计算效率却大大下降。当积分步长从1×10-4 s减小到1×10-6 s时,碰撞力矩的峰值由25.1 N·m增加到25.8 N·m,增加了2.79%,幅值增加相对较小,说明积分步长对碰撞力矩的影响相对较小。
|
图 8 不同积分步长比对碰撞力矩的影响 Figure 8 Contact moment changing with time under different time integral steps |
3 结论
本文采用了含阻尼项碰撞模型模拟桨叶与限动块之间的碰撞,并对桨叶扬起下坠动力学问题做了数值计算。对比分析了扭转弹簧刚度、阻尼比和积分步长对碰撞力矩的影响,结果表明:
(1) 碰撞模型中扭转弹簧刚度增大时,限动块间碰撞力矩的峰值也随之增大,其峰值增大22.0倍,说明该碰撞模型中扭转弹簧刚度对碰撞力矩峰值影响较大。
(2) 碰撞模型中阻尼比增大时,限动块间碰撞力矩的峰值也随之增大,其峰值增大10.4%,增幅相对较小,说明该碰撞模型中阻尼比对碰撞力矩峰值影响较小。
(3) 计算积分步减小时,计算精度相应提高,但计算的效率却大幅度降低。
| [1] | Keller J A, Smith E C, Knarr C R. Experiment/theoretical correlation of analysis for helicopter rotor blade/droop stop impacts[C]//38th Structures, Structural Dynamics and Materials Conference.[S.l]:AIAA, 1997:345-347. |
| [2] | Keller J A, Smith E C. Experiment and theoretical correlation of helicopter rotor blade-droop stop impacts[J]. Journal of Aircraft , 1999, 36 (2) : 443–450. DOI:10.2514/2.2450 |
| [3] | Newman S J. The verification of a theoretical helicopter rotor blade sailing method by means of wind tunnel testing[J]. Aeronautical Journal , 1995, 99 (982) : 41–51. |
| [4] | Geyer W P, Smith E C, Keller J A. Aeroelastic analysis of transient blade dynamics during shipboard engage/disengage operations[J]. Journal of Aircraft , 1998, 35 (3) : 445–453. DOI:10.2514/2.2317 |
| [5] | Kang H, He C, Carico D. Modeling and simulation of rotor engagement and disengagement during shipboard operations[C]// American Helicopter Society 60th Annual Forum Proceedings. Baltimore, MD:[s.n.], 2004. |
| [6] | Bottasso C L, Bauchau O A. Multibody modeling of engage and disengage operations of helicopter rotors[J]. Journal of the American Helicopter Society , 2001, 46 (4) : 290–300. DOI:10.4050/JAHS.46.290 |
| [7] | Wall A S, Langlois R G, Afagh F F. Modeling helicopter blade sailing: Dynamic formulation in the planar case[J]. Journal of Applied Mechanics, Transactions ASME , 2007, 74 (6) : 1104–1113. DOI:10.1115/1.2722766 |
| [8] | Wall A S, Afagh F F, Langlois R G, et al. Modeling helicopter blade sailing: Dynamic formulation and validation[J]. Journal of Applied Mechanics , 2008, 75 (6) : 1055–1062. |
| [9] | Khouli F, Wall A S, Langlois R G, et al. Investigation of the feasibility of a proposed hybrid passive and active control strategy for the transient aeroelastic response of helicopter rotor blades during shipboard engage and disengage operations[C]//American Helicopter Society 64th Annual Forum. Montreal, Canada: [s.n.], 2008. |
| [10] | Khouli F, Wall A S, Afagh F F, et al. Influence of ship motion on the aeroelastic response of a Froude-scaled maritime rotor system[J]. Ocean Engineering , 2012, 54 (3) : 170–181. |
| [11] | Han D, Wang H W, Gao Z. Aeroelastic analysis of a shipboard helicopter rotor with ship motions during engagement and disengagement operations[J]. Aerospace Science and Technology , 2012, 16 (1) : 1–9. DOI:10.1016/j.ast.2011.02.001 |
| [12] |
康浩, 高正.
舰面直升机旋翼瞬态气弹响应分析[J]. 航空动力学报 , 2000, 15 (1) : 67–70.
Kang Hao, Gao Zheng. Aeroelastic response analysis of helicopter rotor during shipboard operation[J]. Journal of Aerospace Power , 2000, 15 (1) : 67–70. |
| [13] |
韩东, 王浩文, 高正.
直升机桨叶扬起下坠碰撞动响应计算[J]. 航空学报 , 2006, 27 (5) : 795–798.
Han Dong, Wang Haowen, Gao Zheng. Computation of dynamic response for helicopter blade droop stop impact[J]. Acta Aeronautica et Astronautica Sinica , 2006, 27 (5) : 795–798. |
| [14] |
韩东, 高正, 王浩文, 等.
铰接式旋翼舰面瞬态气弹响应及参数研究[J]. 空气动力学学报 , 2007, 25 (1) : 7–11.
Han Dong, Gao Zheng, Wang Haowen, et al. Analysis of transient aeroelastic response for shipboard articulate rotor[J]. Acta Aerodynamic Sinica , 2007, 25 (1) : 7–11. |
 2016, Vol. 48
2016, Vol. 48


