下滑进场是直升机着舰过程中的重要环节,在此期间,其飞行品质受到复杂流场环境等因素的干扰,影响直升机的着舰安全。国外对于直升机着舰的研究[1-4]起步较早,对于直升机在舰上的使用与维护、起飞与回收等流程均有较为详细的规定,形成了明确的舰载直升机操作流程手册[5]。手册中指出:直升机在正常着舰时,飞行员需依据风向、海况和指定的操作要求,对准左舷或右舷基准线,进行下滑进场,并悬停到着舰区甲板上方区域随舰跟进。
一般的进场方式可分为左舷进场和右舷进场两种,如图 1所示。飞行员根据所处的位置决定进场路线,首要条件是选取视线较好,更利于飞行员观察的进场方向。此外,根据直升机在航母上的使用限制规定,出于安全的考虑,严禁直升机从停放舰载机的甲板上空飞过,因此,正常进场一般不选用0°进场路线。同时,机库与上层建筑一般在母舰的右侧,因此,直升机以左舷进场的方式较为适合。美国的航母上一般也均标有下滑进场的左舷45°基准线。

|
图 1 下滑进场路线图 Figure 1 Helicopter approach chart |
中国国内对此研究起步较晚,目前在母舰的着舰训练中依然采用0°进场方式,直升机需穿越舰船尾部的气流场,到达指定着舰区域悬停,因此,母舰上也没有标明左舷或右舷进场基准线。
在实际的着舰过程中,除了飞行员视线、甲板建筑等因素外,舰船甲板流场也是影响直升机着舰安全的重要因素。舰船甲板流场作为舰载直升机在近舰与舰面起降过程中的飞行环境,其时空特性使得直升机各部件的气动载荷分布发生变化,影响直升机的飞行品质。尤其在恶劣的海况条件下,流场的非线性和不均匀性严重影响直升机的气动特性,加大了直升机操纵的难度。因此,在下滑进场时,采取合理的着舰策略,能够降低流场对直升机飞行品质的影响,减轻飞行员的工作负荷,提高着舰安全性。
1 飞行动力学建模与验证 1.1 飞行动力学建模本文采用了一种适合复杂流场环境的飞行动力学计算模型[6-8],主要考虑了甲板流场和舰面效应对直升机气动特性的影响。
考虑到风速对直升机气动特性的影响,对桨叶任意叶素剖面气流速度计算公式作适当修改,将旋翼的前进比细化为每片桨叶不同分段位置处的当地前进比μx,y,zij,在当地前进比中考虑当地的流场风速矢量Wx,y,zij,其计算公式为
| ${{\mu }_{x,y,z}}^{ij}=\frac{{{V}_{x,y,z}}-{{W}_{x,y,z}}^{ij}}{\Omega {{R}_{T}}}$ | (1) |
式中:Vx,y,z为直升机运动速度;Ω为旋翼转速;RT为旋翼半径。
则第i片桨叶的第j处分段叶素任意剖面气流速度的量纲化一形式可表示为
| ${{U}_{T,P,R}}^{ij}=f({{\mu }_{x,y,z}}^{ij},p,q,r,{{v}_{i}},{{\beta }_{i}},{{\zeta }_{i}},{{\psi }_{i}})$ | (2) |
式中:p,q,r为机体角速度;vi为旋翼诱导速度;βi,ζi,ψi分别为第i片桨叶的挥舞角、摆振角和方位角。
同时,直升机在舰面甲板上方飞行时,由于舰面甲板效应作用,其旋翼气动特性受到了影响,具体表现在旋翼入流的变化[9]。考虑到舰船运动与直升机相对甲板的飞行位置,旋翼诱导速度可表示为
| ${{v}_{i}}=f({{\mu }_{x,y,z}}^{ij},{{C}_{T}},{{R}_{T}},{{z}_{MR}})~$ | (3) |
式中:CT为旋翼拉力系数;zMR为旋翼相对舰船甲板的垂向距离,与舰船运动和直升机相对甲板的飞行位置相关。
具体的建模过程可参考文献[6]。由此,得到复杂流场环境下的直升机非线性运动方程组
| $\dot{X}~=f\left( X,U,W,t \right)$ | (4) |
式中:U=[θcol,θlat,θlon,θped]T为操纵输入;W为流场风速矢量。状态向量X定义为
| $X={{[{{X}_{bd}},{{X}_{flap}},{{X}_{lag}},{{X}_{induced}},{{X}_{MR}}]}^{T}}$ | (5) |
式中:Xbd=[u,v,w,p,q,r,φb,$\vartheta $b,ψb]T为机体运动向量,包括机体线速率、角速率和机体姿态角;Xflap=[β1,…,NBS,${\dot{\beta }}$1,…,NBS]T为桨叶挥舞运动量,NBS为桨叶片数;Xlag=[ζ1,…,NBS,1,…,NBS]T为桨叶摆振运动量;Xinduced=[λ0,λc,λs,λTR]T为旋翼和尾桨的入流状态量;XMR=[ψ,θdytip]T为包括桨叶方位角和桨叶弹性变形引起的桨距角变化量。
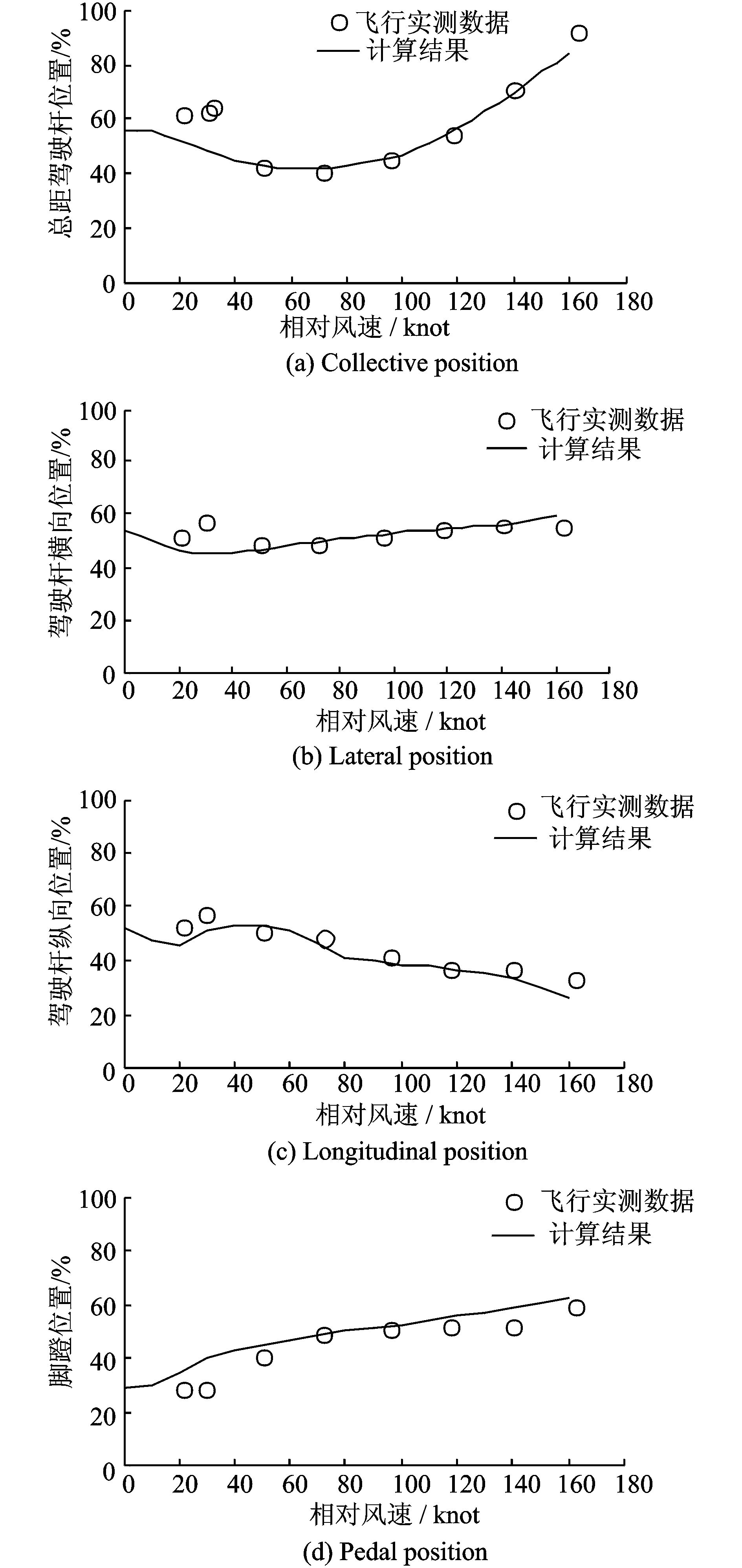
1.2 计算模型的验证验证本文计算模型的准确性,计算UH-60A直升机悬停和匀速前飞状态下的配平计算结果,并与飞行实测数据[10]进行对比验证,见图 2。UH-60A直升机全机、旋翼、尾桨和尾翼的具体数据参考文献[11],为了便于与飞测数据进行对比,驾驶员操纵输入以总距杆、驾驶杆和脚蹬行程百分比的形式给出。
|
图 2 操纵量变化趋势 Figure 2 Variation trend of control sets |
由图 2可以看出,在悬停(相对风速为0) 和低速前飞状态(相对风速小于50节)下,操纵量与飞测值存在一定的误差,尤其是旋翼总距杆位置约有10%的最大误差,一方面是由于本文在建模时采用了动态入流模型,该理论的基础是作用盘理论和加速度势理论[12],在悬停或低速飞行状态下,动态入流理论的假设条件并不完全成立,因此,其准确性一直都备受质疑[13];另一方面可能由飞测试验误差引起,因为悬停或小速度状态下直升机的动稳定性较差,驾驶员需要实时调整操纵量保持直升机的稳定,可能造成测量的误差。在中高速状态(相对风速大于50节)下则不存在这个问题,误差基本保持在5%以内,与飞行测试数据吻合较好。综上所述,本文的直升机计算模型基本满足了工程计算的需求。
2 舰船甲板流场建模 2.1 流场计算模型以国外某型航母为例,对舰上建筑与部件的形状作适当简化,忽略对舰面流场影响较小的建筑与部件。对母舰甲板上方流场的CFD计算,通过FLUENT有限体积法求解器完成。将整个流场看作不可压有黏流动,遵循流体力学运动的基本原理,控制方程采用定常不可压N-S方程,并应用分离涡模拟湍流模型,捕捉精密网格区域的大尺度湍流结构。
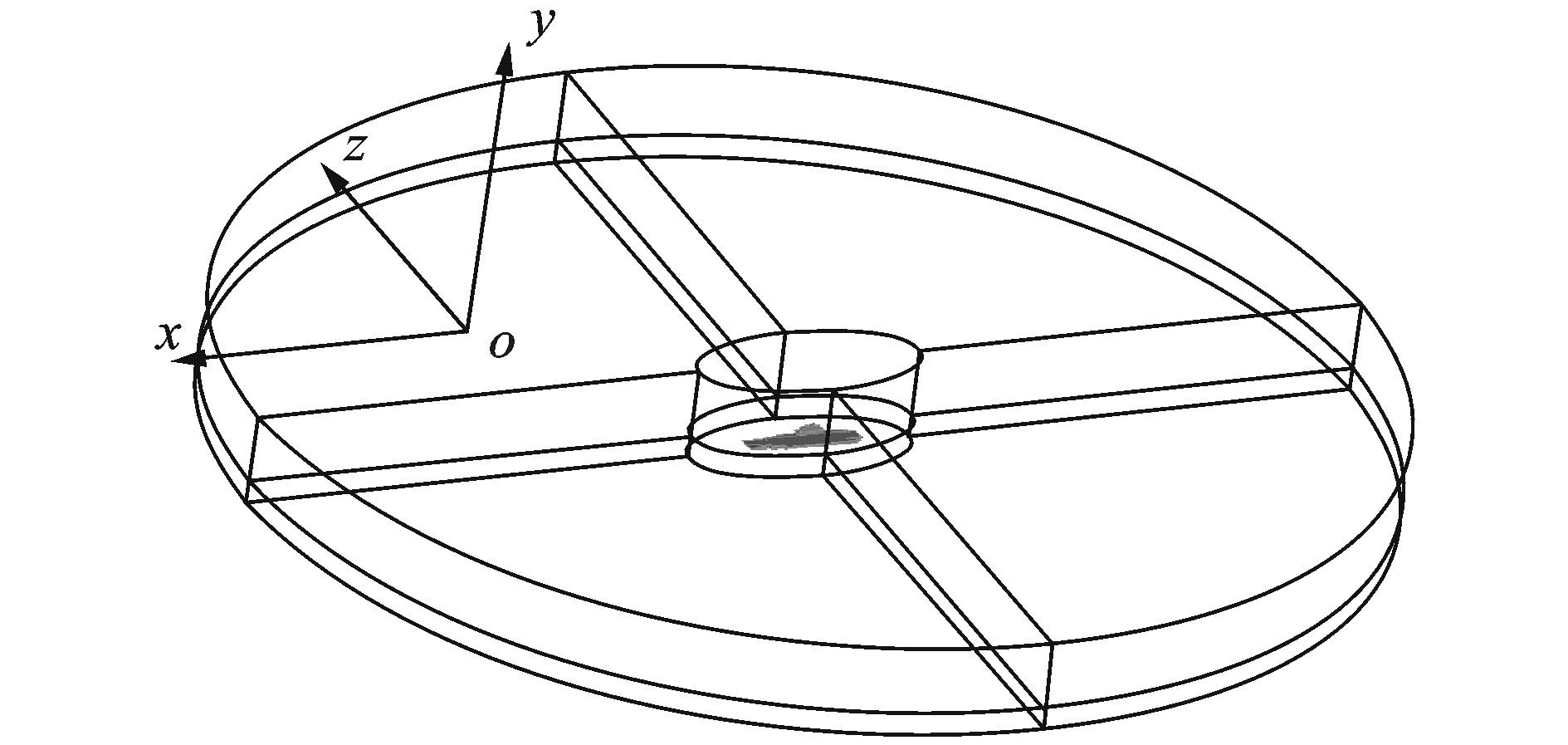
2.2 网格划分与边界条件如图 3所示,在计算域中心设置一个扁椭圆柱体作为放置船体模型的子区域,这种拓扑结构通过控制外边界纵轴和横轴的速度分量改变风向角,可避免重新划分网格。柱体计算域半径取4.5倍模型长度,高度取0.75倍模型长度,在该计算域内,认为计算边界不受舰船附近气流流动的影响。计算域采用混合非结构网格:采用棱柱单元捕捉边界层,在椭圆体子区域内采用四面体子单元,计算域的其余部分则采用非结构网格。使用尺寸函数确保随着远离船体网格尺寸逐渐增大,同时在计算中根据气流速度梯度对网格进行局部自适应加密,以便更好地捕捉涡流。本文主要对母舰甲板上方附近进行网格局部加密,以精确模拟甲板上方的气流场,网格总数约800万个。
|
图 3 用于CFD计算的网格拓扑结构 Figure 3 Network topology structure for CFD |
舰船表面的流场速度设置为与物面相切,假定控制域气流入口和出口的位置离舰船足够远,来流未受舰体扰动的影响,将控制域入口设为速度入口,出口设为压力出口。
2.3 与直升机模型的影响舰船甲板流场与直升机自身流场之间存在影响,考虑到直升机旋翼机体流场的耦合,旋翼对机体、尾翼以及机体对尾翼的下洗、侧洗,使得流场问题更为复杂。为方便研究,本文暂不考虑直升机在下滑进场飞行时与舰船甲板流场之间的相互影响。
舰船甲板流场数值计算的验证具体参考文献[6]。由于篇幅原因,本文不再重复。
3 计算结果与分析 3.1 下滑进场区域本文以UH-60A直升机在上述航母的下滑进场为研究示例,根据母舰甲板上方建筑布置以及样例直升机构造,采取左舷进场方式对驾驶员的视线和操纵较为有利。为研究需要,选取母舰靠近舰尾处的起降位区域作为着舰点,直升机分别沿0°,45°和90°三条路线下滑到达该区域悬停,进场路线如图 4所示。图中,流场的坐标系以该着舰区域中心为坐标原点,沿舰艏方向为X轴,侧向右方向为Y轴,阴影部分为直升机下滑过程中经历的流场区域。

|
图 4 下滑进场路线图 Figure 4 Helicopter landing and approach chart |
3.2 流场等值线云图
由于直升机旋翼机体流场耦合问题较为复杂,本文暂不考虑直升机在下滑进场区域飞行时对流场的影响。
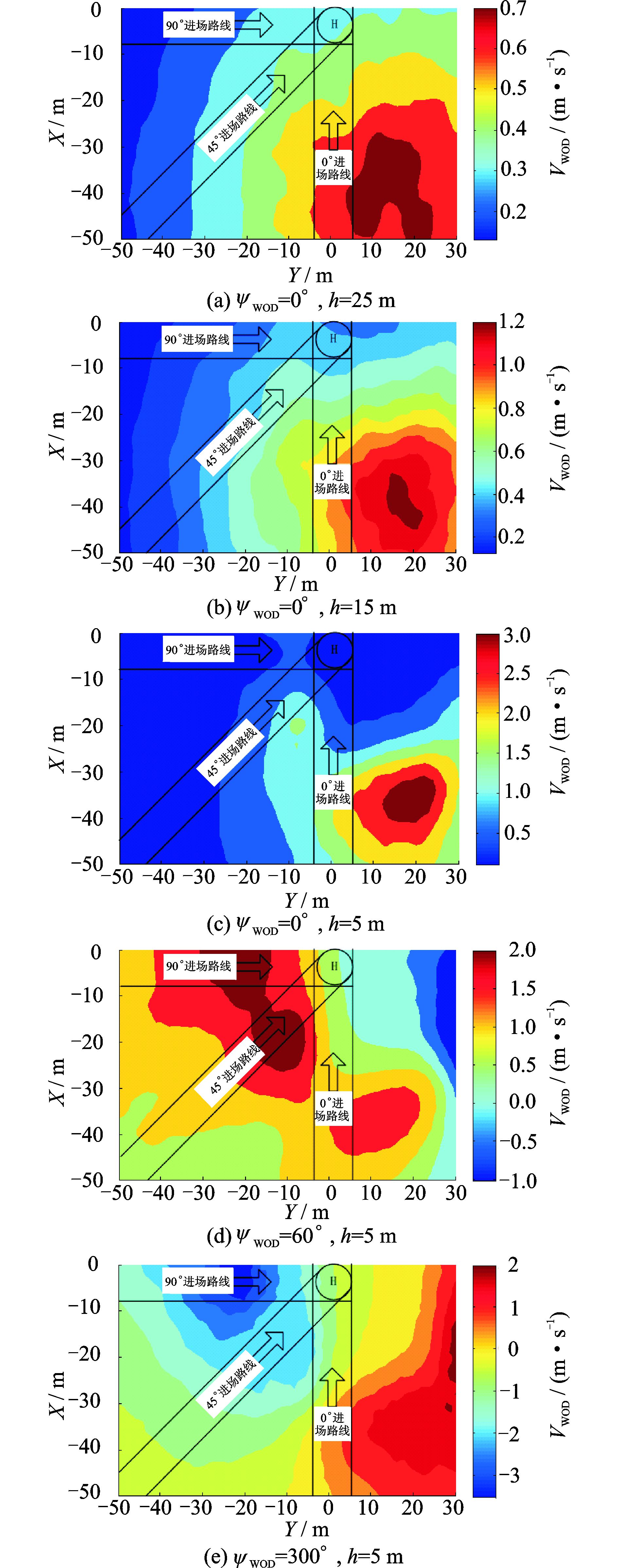
采用CFD方法计算舰船甲板流场,设定计算条件为:甲板风(Wind on deck,WOD)速度VWOD=15 m/s,风向角分别为ψWOD=0°,60°,300°。图 5所示为距离甲板高度h=25,15,5 m处水平截面的垂向气流等值线云图,流场区域与坐标同图 4中所示。
|
图 5 不同高度下的垂向气流等值线云图 Figure 5 Contour maps of vertical airflow at different heights |
由图 5(a~c)可知,在相同甲板风向角的情况下,下洗气流的分布与直升机距离舰面飞行甲板的高度相关。一般而言,高度越低,气流数值范围越大,平均下洗气流值也越大;由图 5(c~e)可知,下洗气流的分布与甲板风向角相关;ψWOD=0°,即甲板风迎舰艏方向吹来时,0°进场路线区域的下洗气流要明显大于左舷方向的气流;ψWOD=60°时,左舷45°和90°进场路线之间区域的下洗气流要较大一些;ψWOD=300°时,左舷90°进场路线区域的下洗气流明显大于左舷45°和0°方向的气流,相对而言,0°进场路线区域的气流较为平缓。
下洗气流的非线性、不规则等特性会造成旋翼桨盘的气流分布的不均匀,改变旋翼的气动特性,影响直升机的飞行姿态和品质。在实际的着舰过程中,考虑到固定翼飞机着舰的需求,母舰一般逆风行驶,甲板风向角一般较小,即下洗气流主要集中在0°进场路线区域上。因此,0°进场方式对于直升机着舰的安全是较为不利的。
3.3 直升机平衡状态量根据舰载直升机操纵流场手册[5]规定,飞行员开始进场时,到达空中滑行或悬停位置,对准下滑线,下滑线距飞行甲板的距离约为3倍旋翼直径,高度为海面以上至少50英尺(黑鹰直升机为75英尺),并根据需要调整至飞行甲板的预计进场航线。在进场时,直升机的下降速率一般不超过50 m/min。
因此,本文设置计算的起始条件为:下滑进场起始点距离舰面甲板的高度为h=23 m,根据不同进场路线计算确定直升机在空间中经历的具体位置,终点为图 4所示的着舰区域,进入悬停跟进阶段,此时直升机在甲板上方的高度为h=5 m。下滑过程中直升机的航迹飞行速度为:vX=2.8 m/s,vY=0 m/s,vZ=0.83 m/s。依据进场航向转换到母舰坐标系,在计算直升机的平衡状态量时不考虑紊流扰动的影响,同时考虑舰面甲板效应。
在此条件下,计算ψWOD=0°,60°,300°流场条件下的直升机平衡状态量,如表 1~3所示。为便于对比分析,表中分别给出了在下滑进场过程中直升机各状态量的最大值和最小值。其中,操纵量均以操纵杆行程百分比的形式给出。
| 表 1 ψWOD=0°流场条件下直升机平衡状态量 Table 1 Helicopter trim states in ψWOD=0° |
| 表 2 ψWOD=60°流场条件下直升机平衡状态量 Table 2 Helicopter trim states in ψWOD=60° |
| 表 3 ψWOD=300°流场条件下直升机平衡状态量 Table 3 Helicopter trim states in ψWOD=300° |
分析表 1~3可知,在旋翼所需功率方面,ψWOD=0°时,直升机以0°进场方式的旋翼所需功率最小;ψWOD=60°时,直升机以45°进场方式的旋翼所需功率最小;ψWOD=300°时,直升机以90°进场方式的旋翼所需功率最小。这是由于在不同流场条件下,直升机采取迎风的进场方式受到的侧风最小,因此旋翼所需功率也相应更小。一般情况下,旋翼所需功率越小越有利于直升机的飞行安全,而在ψWOD=0°时,90°进场方式的旋翼所需功率太大,因此不该采取此种进场方式。但是,旋翼所需功率仅是其中一项参考依据,3.2节分析表明0°进场方式并不利于直升机的着舰安全。同时,直升机在45°进场方式的旋翼所需功率并没有超过限制范围,因此,当ψWOD=0°时,采取45°进场方式是较为合理的。
在操纵量方面,3种进场方式下直升机的总距杆及驾驶杆位置是较为接近的,主要影响的是脚蹬位置。这是由于直升机采用不同的进场方式,航向角的差别导致直升机受到的侧风干扰不同,而侧风正是影响尾桨总距的重要因素。其中,ψWOD=300°时,采用90°进场方式,直升机是顺风方向,所需操纵量变大,尤其是尾桨总距甚至超过了操纵限制,这在现实中是绝不允许的。
在机体姿态方面,直升机的变化幅度不大,表明各自进场路线区域内的流场变化对直升机姿态的影响较小。但是,不同进场方式下的机体姿态角差异较大,尤其在ψWOD=0°时采用90°进场方式,以及在ψWOD=300°时采用45°进场方式,滚转角甚至超过了7°,这是由于直升机滚转通道的动稳定性较差,直升机在进场时所受侧风过大,严重影响直升机的飞行品质与安全。因此,直升机在进场时如能沿甲板风向角ψWOD=0°或附近的方向下滑进场,能够最大程度地避免侧风影响,利于着舰安全。
4 结论(1) 不同WOD条件下的舰船甲板流场分布分析表明,流场的分布与距离甲板的高度相关,且下洗气流主要集中在迎风方向的路线区域。
(2) 不同WOD条件下直升机平衡时的旋翼所需功率、操纵量和机体姿态方面的分析表明,合理的进场方式有利于着舰安全。
(3) 直升机处于在甲板风向角ψWOD=0°附近的流场条件下,驾驶员宜采用左舷45°的进场方式,能够减少流场对着舰的影响;在特殊情况下,母舰的行驶方向与甲板风存在一定的夹角,为避免侧风对直升机飞行姿态和操纵量的影响,驾驶员宜调整直升机航向,保持迎风方向进场,能够减少流场的干扰,提高着舰的安全性。
| [1] | Wilkinson C H, VanderVliet G M, Roscoe M F. Modeling and simulation of the ship-helicopter environment[C]// Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit. Denver, Colorado:[s.n.], 2000: 4583-4894. |
| [2] | VanderVliet G M, Wilkinson C H, Roscoe M F. Verification, validation and accreditation of a flight simulation: The JSHIP experience[C]// Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit. Montreal, Canada:[s.n.],2001: 4061-4072. |
| [3] | Roscoe M F, Wilkinson C H. DIMSS-JSHIP′s modeling and simulation process for ship/helicopter testing and training[C]//Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit. Monterey, California:[s.n.], 2002: 4597-4608. |
| [4] | Smallhorn C C, Wilkinson C H, VanderVliet G M. A piloted evaluation of a ship deck landing trainingsimulation[C]// Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit. San Francisco, California:[s.n.], 2005: 6295-6305. |
| [5] | U.S. Coast Guard. Joint tactics, techniques, and procedures for shipboard helicopter operations[R]. M3710.2E, 2011. |
| [6] |
徐广, 胡国才, 王允良, 等.
直升机在复杂舰面流场中的悬停研究[J]. 南京航空航天大学学报 , 2015, 47 (2) : 205–211.
Xu Guang, Hu Guocai, Wang Yunliang, et al. Research on helicopter hover on flight deck in complicated airflow field[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2015, 47 (2) : 205–211. |
| [7] |
吉洪蕾, 陈仁良, 李攀.
适用于直升机飞行力学分析的三维空间大气紊流模型[J]. 航空学报 , 2014, 35 (7) : 1825–1835.
Ji Honglei, Chen Renliang, Li Pan. A model of three-dimensional-field atmospheric turbulence for helicopter flight dynamics analysis[J]. Acta Aeronautica et Astronautica Sinica , 2014, 35 (7) : 1825–1835. |
| [8] |
徐广, 胡国才, 陶杨, 等.
舰面流场下的直升机平衡特性分析[J]. 飞行力学 , 2015, 33 (2) : 116–119.
Xu Guang, Hu Guocai, Tao Yang, et al. Analysis of shipborne helicopter trim characteristics in airwake[J]. Flight Dynamics , 2015, 33 (2) : 116–119. |
| [9] | Xin H, Prased J V R, Peters D A. Dynamic inflow modeling for simulation of a helicopter operating in ground effect[C]//Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit. Portland, OR:[s.n.], 1999,DOI:org/10.2514/6.1999-4114. |
| [10] | Ballin M G. Validation of a real-time engineering simulation of the UH-60A helicopter[R]. NASA-TM-88360, 1987. |
| [11] | Howlett J J. UH-60A Black Hawk engineering simulation program [R]. NASA-CR-166309, 1981. |
| [12] | Stepniewski W Z. Rotary-wing aerodynamics, Volume I: Basic theories of rotor aerodynamics (with application to helicopter)[R]. NASA-CR-3082, 1979: 241-243. |
| [13] | Kothmann B D, Keller J D, Curtiss H C. On aerodynamic modeling for rotorcraft flight dynamics [C]// Proceedings of the 22nd European Rotorcraft Forum. Brighton, UK:[s.n.], 1996. |
 2016, Vol. 48
2016, Vol. 48


