直升机旋翼流场的一个重要特点就是旋翼在旋转过程中产生强烈的桨尖涡和尾迹流动,影响后续桨叶,产生桨涡干扰,桨涡干扰是旋翼流动重要的噪声源,并会导致桨叶出现非定常气动载荷、结构振动等现象,在直升机下降飞行和水平飞行过程中影响尤为明显。控制桨尖涡的位置和强度能有效抑制桨涡干扰噪声、减小振动,常见的控制方法包括桨尖修形、增加扰流装置(副翼、扰流板)及一些主动流动控制等。
开槽桨尖是一种对桨尖涡进行控制的被动流动控制方法[1-3],其基本原理是通过开槽将桨叶前缘的高速来流导入,从桨叶侧缘喷出,被导入气体位于桨尖涡形成的核心区域当中,通过增大桨尖涡核心区域的物理耗散,达到减弱桨尖涡强度的目的。开槽桨尖控制实验研究表明[3],桨尖涡在向后发展的初期阶段其衰减程度可以忽略不计,旋涡涡核内部为层流流动,旋涡的高速旋转抑制了湍流的生成,涡核外围依次为转捩区和湍流区域。开槽桨尖通过导入气流到涡核中心区域,破坏了旋涡的这种抑制湍流生成的机理,在桨尖涡的生成和早期发展阶段增大了旋涡的耗散。
本文通过模拟旋翼悬停状态下的流动,对开槽桨尖流动控制进行了研究。在数值计算中,通过改进计算方法和网格加密,提高了旋翼桨尖涡的模拟精度,为分析旋涡流动创造了条件。研究中对比了方形桨尖和不同开孔形式的开槽桨尖的旋涡强度和旋翼性能,从旋涡形成和发展过程,对控制机理进行了分析。
1 数值方法计算采用笔者所在课题组自行研发的并行多块结构化网格数值计算软件PMB3D完成,控制方程为旋转坐标系下的三维可压缩雷诺平均N-S方程。流体速度矢量q=u,v,w在旋转坐标系下用绝对速度表示[4-5]。采用旋转坐标系以后,旋翼悬停流场变换为定常流场进行计算[6-7],同时流场具有旋转对称性的特点,因此只需要对其中一片桨叶进行求解,两侧的周向边界指定为周期性边界条件。
悬停流场假设为全湍流流动,采用一方程Spalart-Allmaras(S-A)湍流模型[8],模型方程的量纲化一形式如下[9]
| $\partial v/\partial t={{S}_{P}}\left( v \right)+{{S}_{D}}\left( v \right)+D\left( v \right)-C\left( v \right)$ | (1) |
式中:v为涡黏性系数控制变量;右端项SP为湍流生成项;SD为湍流破坏项;C和D分别为对流项和耗散项,其中标准S-A模型的生成源项为
| ${{S}_{P}}={{C}_{b1}}\left[ 1{{f}_{t2}} \right]S\upsilon $ | (2) |
式中:S为旋转张量的模。研究表明,S-A模型的标准生成源项对于旋涡流动会产生过大的湍流耗散,文献[10, 11]介绍了针对旋转流动的修正公式,思想是在生成源项中对旋转张量和变形张量进行比较,如果旋转张量的模大于变形张量的模(对应旋涡情况),则减小湍流量的生成,如果旋转张量的模与变形张量相当或者小于变形张量(对应薄剪切层情况),则维持原来的生成源项不变。具体为将式(2) 中的S用式(3) 代替
| $S\equiv \left| {{\Omega }_{ij}} \right|+{{C}_{prod}}min(0,\left| {{S}_{ij}} \right|-\left| {{\Omega }_{ij}} \right|)~$ | (3) |
式中:Ωij代表旋转张量,|Ωij|=
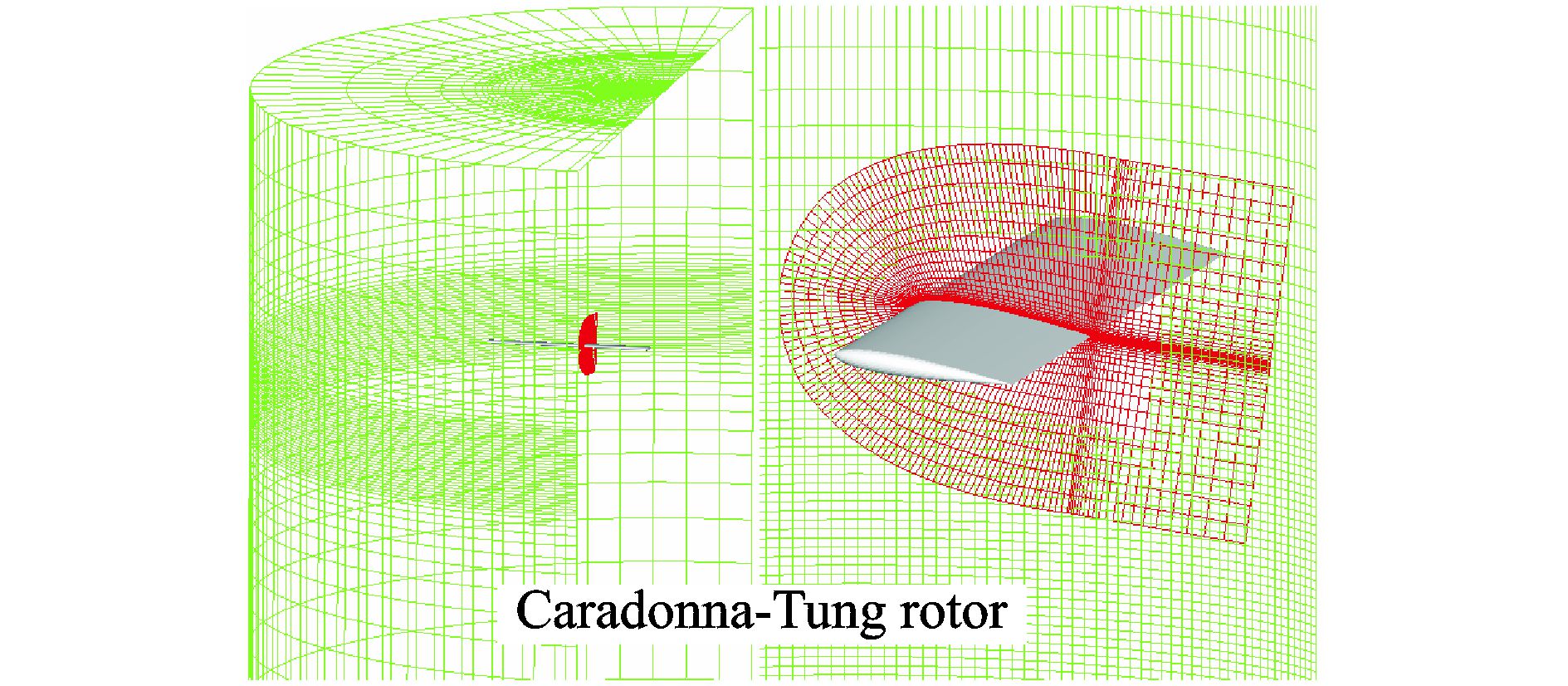
选择Caradonna-Tung旋翼[12]作为基本构型,该旋翼具有简单的解析几何外形,包含了比较丰富的表面压力和尾迹测量数据,目前已成为旋翼研究的标准模型之一。该旋翼包括两片桨叶,每片桨叶为等弦长无扭转的直翼,翼剖面形状为NACA-0012翼型。桨盘半径为1.143 m,桨叶展弦比为6。计算中对外形进行了适当简化,忽略了桨毂和连杆的影响,同时将桨根切除部分取为桨盘半径的1/10,桨叶桨尖为方形桨尖。
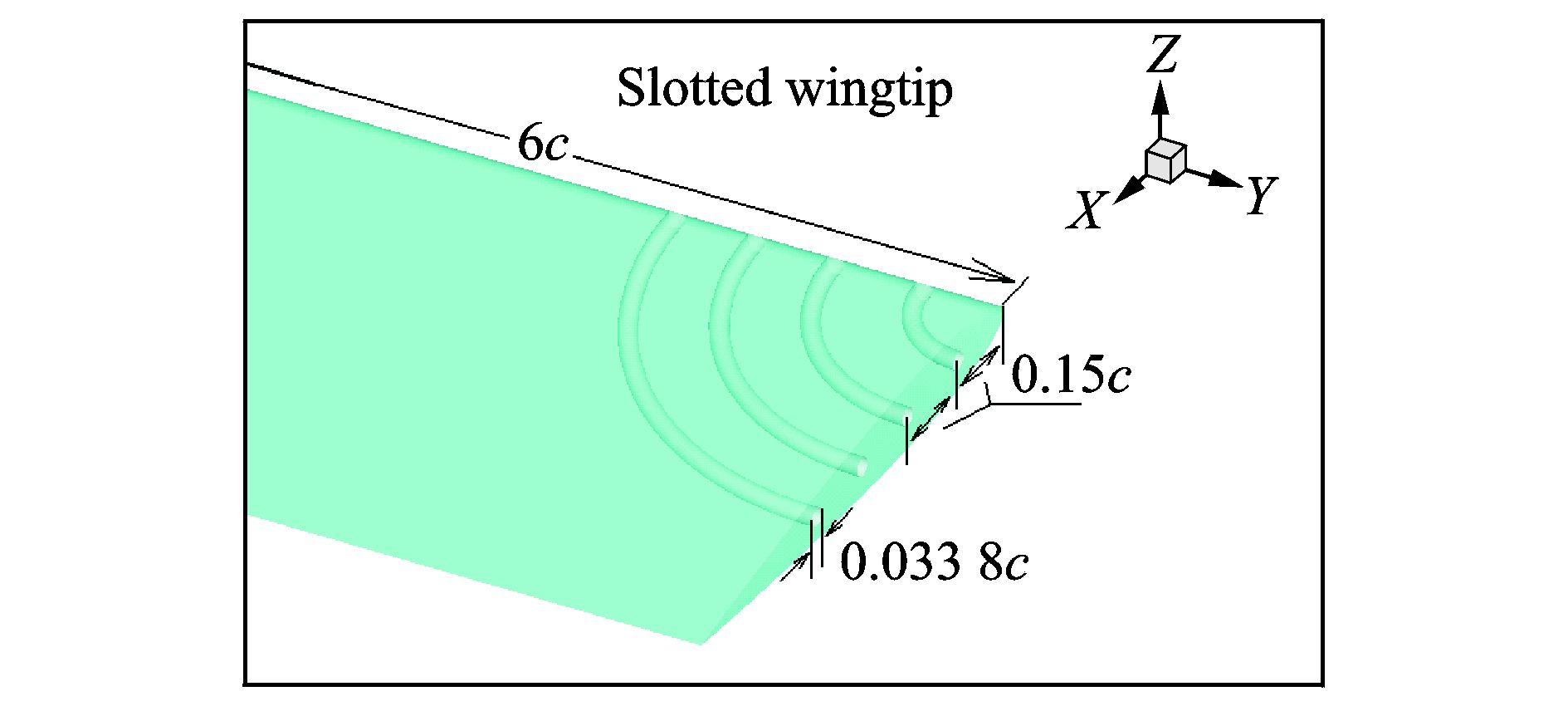
开孔桨尖外形如图 1所示,从图中可以看到,桨尖截面上沿弦长方向排列有4个小孔,分别和桨叶前缘相连通,这样从前缘进入的气体被引入到绕桨尖流动当中,即和桨尖涡流动进行掺混,起到控制桨尖流动的作用。图 1中c为桨叶弦长,开孔位置分别为距前缘15%,30%,45%和60%弦长处,圆孔中心位置位于弦线上,孔的直径为3.38%c。槽道的平面形状为半圆,前缘开孔中心位于前缘线上,孔径保持不变。图 2给出了桨尖网格局部放大图,从中可以看到槽道内部和桨尖截面的网格分布。为了消除计算网格带来的差异,所有外形的计算网格都是在4孔开槽桨尖网格的基础上得到,少一个孔就将开槽通道内的网格删除,槽道的进出口设置为固壁边界条件,其他地方网格保持不变,这样保证了不同外形之间的网格一致性。
|
图 1 开槽桨尖外形 Figure 1 Configuration of slotted blade tip |

|
图 2 桨尖结构化网格 Figure 2 Structured grids on blade tip |
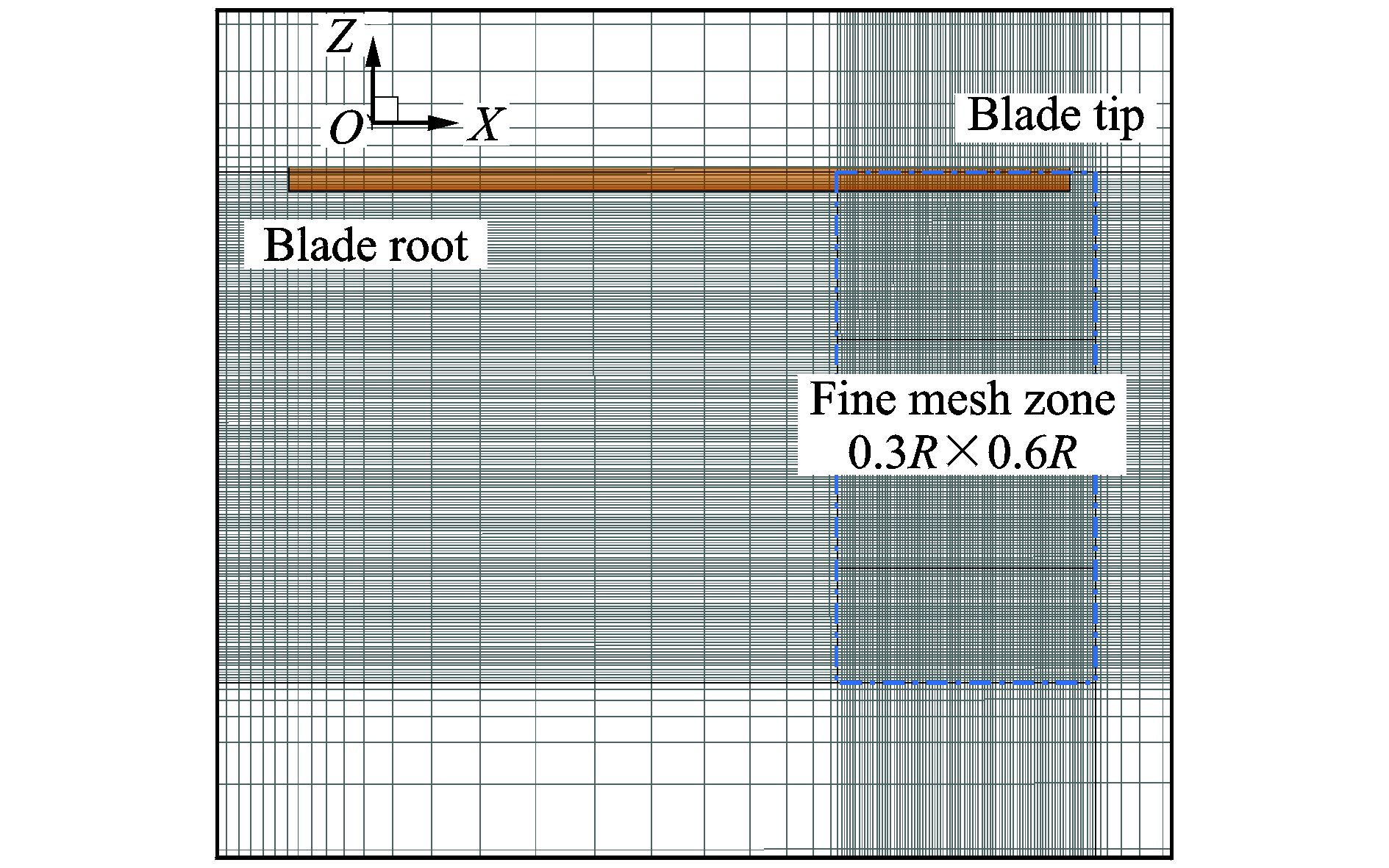
计算网格采用重叠网格,如图 3所示,围绕旋翼桨叶生成的是C型网格,周向和法向的网格数量分别为477和57,第1层网格距离物面的距离为1×10-5倍弦长。为了很好地模拟桨尖形状,围绕桨尖生成了单独的C型网格块,和内侧网格块之间满足对接关系。外围的背景网格为O型,为尽量减小远场边界对流场的影响,将周向和旋翼上方的边界取为100倍弦长,旋翼下方的边界取为150倍弦长。为了精细捕捉旋翼桨尖涡流动,考察开槽桨尖吹气流动控制对桨尖涡的影响,在桨尖涡生成和向下发展的一段区域内对网格进行了加密。经验表明,桨尖涡大小约为桨尖弦长c的1/10,二阶格式捕捉旋涡的要求是在旋涡截面两个方向上各布置10个网格点,因此在网格加密区域内网格间距定为0.01c,同时由于悬停状态下桨尖涡向内收缩和向下游发展,以涡心轨迹的试验数据[7]为参考,将从翼尖外侧0.03R位置开始向内0.3R距离,向下0.6R距离范围定义为网格加密区,图 4给出了加密区域的网格示意图,为方便显示,图中的网格数量为实际数量的1/2。局部加密增大了总的网格规模,背景网格的数量为281(径向)×241(周向)×445(法向),网格单元总数约为4 320万个。
|
图 3 重叠网格 Figure 3 Overlap grids |
|
图 4 捕捉桨尖涡的网格加密区 Figure 4 Refined grids for blade tip vortex |
亚声速悬停状态的参数为:桨尖马赫数Matip=0.44,总距角θc=8°,基于桨尖速度和弦长的雷诺数Re=1.92×106。数值计算在旋转坐标系下进行,由于两片桨叶的流场相同,因此只需要对单片桨叶流场进行计算,在周向方向上采用周期性边界条件。计算采用定常计算方法,时间上采用点隐式的LU-SGS算法,空间上采用Roe通量差分分裂格式,边界面上物理量采用三阶MUSCL插值方法。
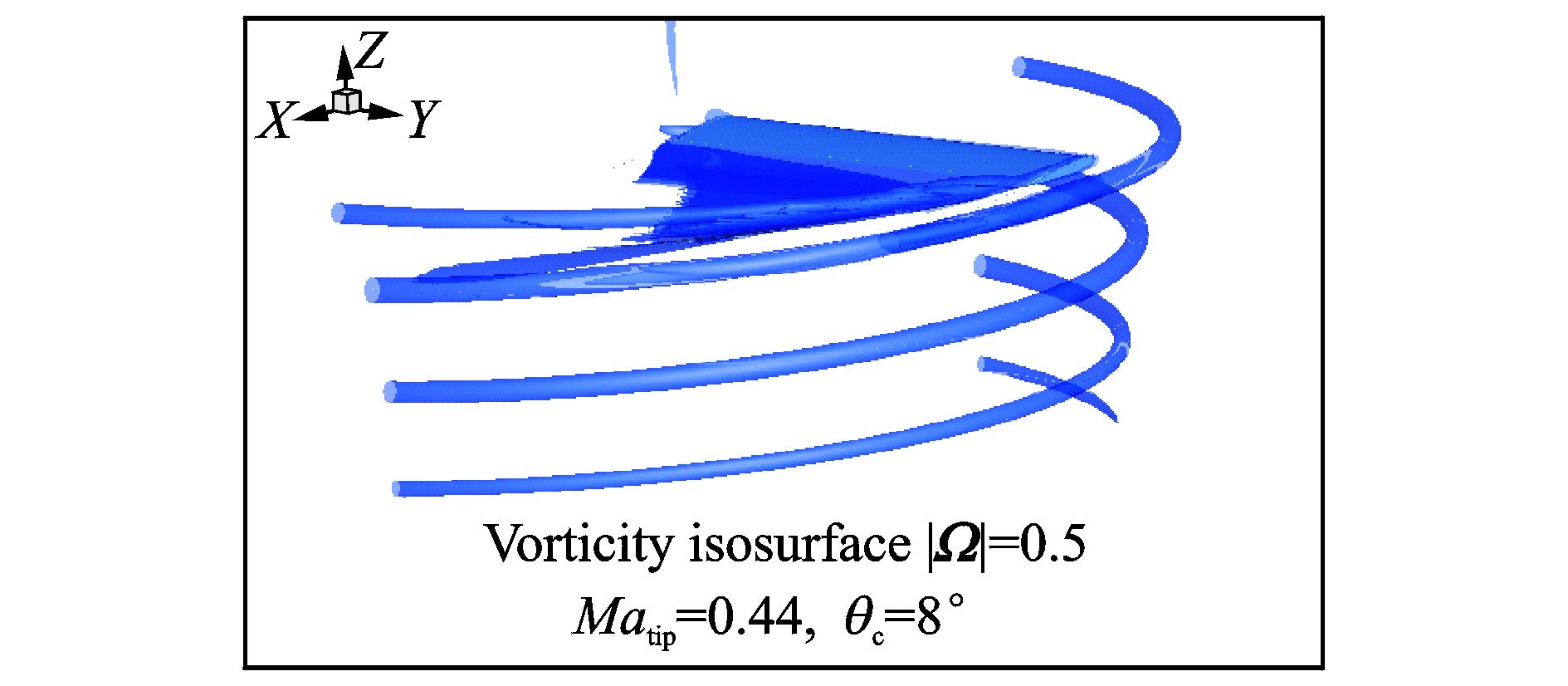
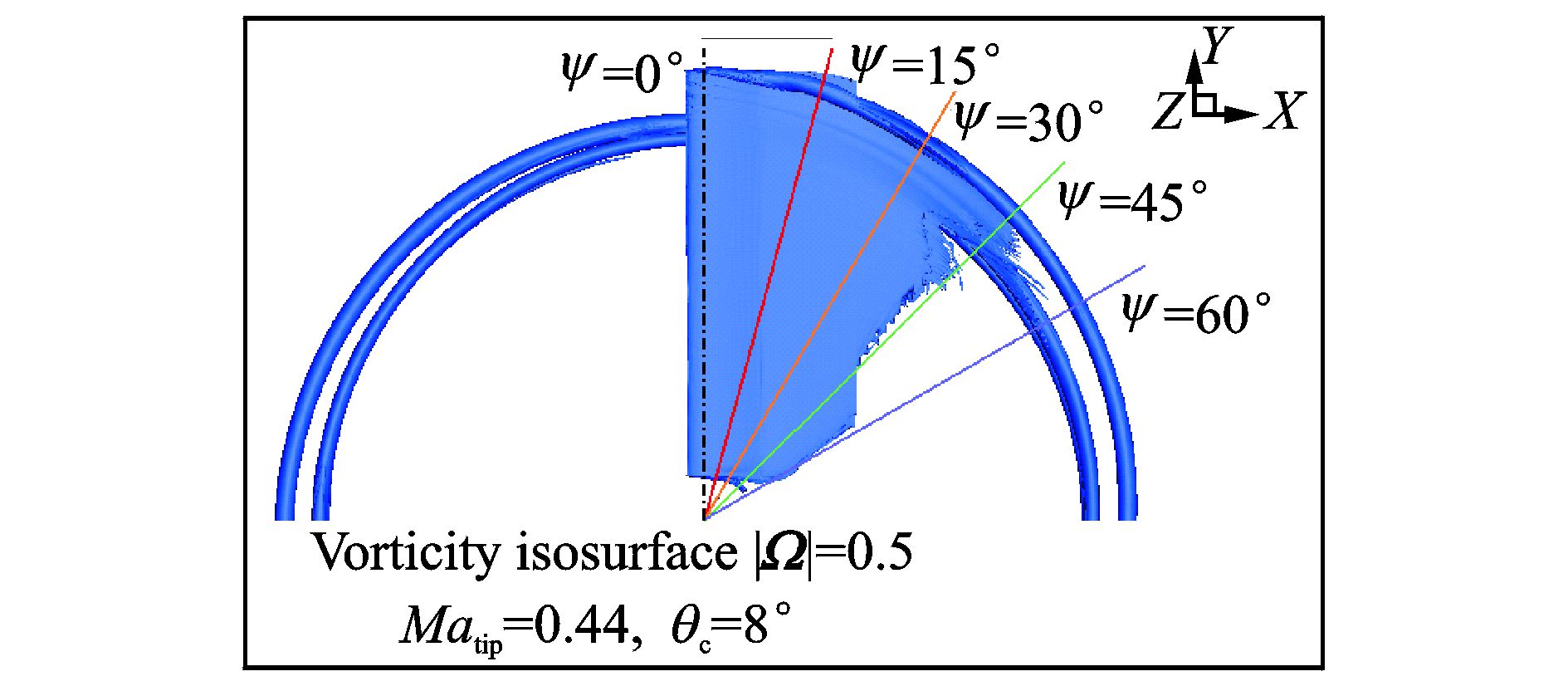
2.1 基本外形图 5给出了Caradonna-Tung旋翼在悬停状态下的涡量等值面图,其中等值面代表的涡量模|Ω|=0.5,从图中可以看到,当前计算对桨尖涡的分辨率较高,最大尾迹角大于630°。当尾迹角进一步增大时,桨尖涡的位置超出了预定的网格加密区域,涡的数值耗散大于其物理耗散,涡的强度迅速变弱直到消失。
|
图 5 涡量等值面侧视图 Figure 5 Side view of vorticity isosurface |
图 6给出了旋翼的尾迹截面示意图,尾迹截面通过旋翼转轴,与桨盘平面相互垂直,4个截面分别对应尾迹角ψ=15°,30°,45°,60°。图 7给出了不同尾迹截面上的涡量云图,可以看到每个截面上有4个旋涡,从上到下每个旋涡之间尾迹角相差180°,随尾迹角增大,旋涡直径增大,旋涡强度减弱。当尾迹角ψ=15°时,桨尖涡从翼尖脱出,旋涡还没有形成规则的圆形,与桨尖涡连为一体的是物面的附面层结构。当桨尖涡尾迹角从15°增大到30°时,集中涡呈更加规则的圆形,同时附面层尾迹受到旋翼下洗速度的影响向下发展,并且其向下发展的速度大于桨尖涡,当桨尖涡尾迹角ψ=60°时,第1排的附面层尾迹(ψ=60°)靠近第2排的桨尖涡(ψ=240°),受第2排桨尖涡旋转速度的影响,尾迹形状向旋涡方向弯曲。由于附面层尾迹和桨尖涡向下发展的速度不一致,两者并不始终连为一体,这可以解释为什么看到的桨尖涡有4个而附面层尾迹只有两条。
|
图 6 涡量等值面俯视图 Figure 6 Top view of vorticity isosurface |

|
图 7 不同尾迹角截面的涡量云图 Figure 7 Vorticity contour at different wake ages |
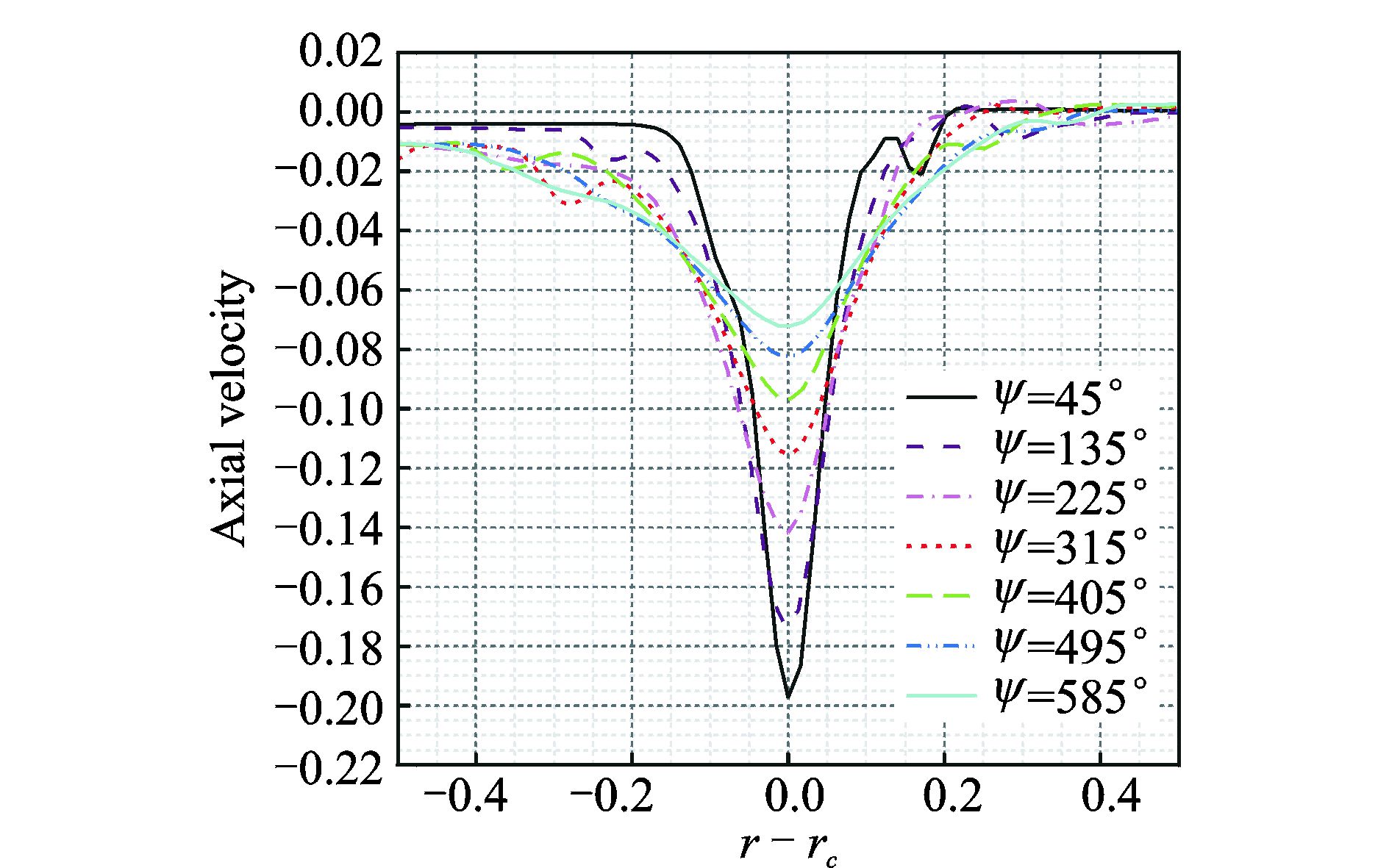
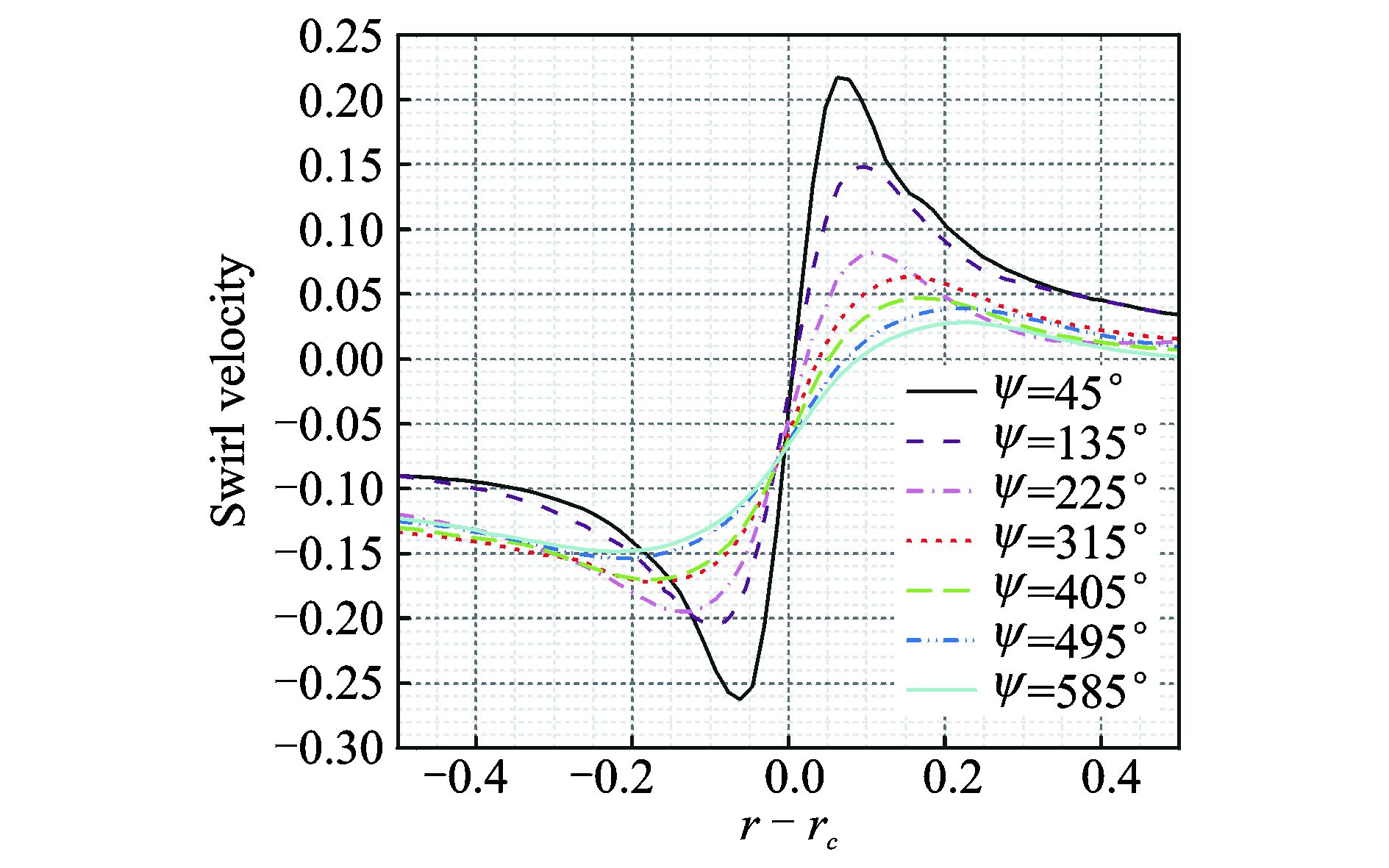
图 8给出了桨尖涡轴向速度分布随尾迹角的变化,其中轴向速度用桨尖速度进行了量纲化一,从图中可以看到,桨尖涡的轴向速度为负值,射流分布呈尾流型(Wake-like)[4],区别于射流型(Jet-like)速度分布。随尾迹角增大,峰值速度的绝对值减小,射流宽度增大。图 9给出了桨尖涡旋转速度分布随尾迹角的变化。图中横坐标r-rc表示距旋涡中心的距离,旋转速度用桨尖速度进行量纲化一,从图中可以看到,当前计算得到的旋转速度分布和旋涡模型[2]相似,由于旋涡处在旋翼的下洗流场当中,涡心速度不等于0,速度方向向下。由于旋涡的旋转运动,涡心两侧旋转速度方向相反,旋转速度最大值与涡心的距离定义为涡核半径,从图 9中可以看到,随尾迹角增大,桨尖涡的峰值旋转速度减小,涡核半径增大。
|
图 8 桨尖涡轴向速度分布随尾迹角的变化 Figure 8 Axial velocities at different wake ages |
|
图 9 桨尖涡旋转速度分布随尾迹角的变化 Figure 9 Swirl velocities at different wake ages |
2.2 开槽桨尖外形
开槽桨尖外形的计算状态和基本外形相同,即悬停状态,桨尖马赫数Matip=0.44,总距角θc=8°。开槽桨尖是通过圆弧形管道将桨叶前缘的气体导入到翼尖喷出,起到增大桨尖涡耗散,减弱桨尖涡强度的作用;另一方面,开槽桨尖改变了桨叶形状,增大了型阻,对旋翼性能有负面的影响。流动控制需要在达到控制目的的同时尽量减少性能的损失,为了研究开孔多少和开孔位置的影响,本文对4种形式的开槽桨尖进行了对比研究,具体来说是4个开孔的圆心位于翼尖弦长的15%,30%,45%和60%位置,分别定义为1,2,3和4号位,本文共研究了12,13,14和1234四种组合模式,其中12模式表示1号和2号孔为通气状态,其余孔为封闭状态。
桨尖涡在桨叶叶梢生成并拖出,旋涡的旋转方向是从桨叶的迎风面到背风面,开槽桨尖通过引入气体到旋涡的中心区域,一则破坏旋涡的有序流动结构,二则增大旋涡内部的耗散机制,达到削弱桨尖涡强度的目的。为了清楚地了解开槽桨尖对桨尖涡生成过程的影响,图 10给出了基本外形和开槽桨尖外形在桨尖附近的涡量等值线比较。从图 10(a)中可以看到,桨尖涡的形成是由背风面旋涡和侧面旋涡的合成结果,两个旋涡的旋转方向相同,在两者合成到一起之前能看到两个独立的旋涡及其次生旋涡,在叶型末端两者合成为1个旋涡,此时旋涡的形状还不规则,在旋转作用下旋涡将演变成为更加规则的圆形。图 10(b)给出了开两孔模式的开槽桨尖流动图像,此时由于有横向流动进入到旋涡内部,破坏了侧面旋涡的结构,从前面第1个截面可以看到侧面旋涡的尺寸增大,形状变得很不规则;从第2个截面上观察,侧面旋涡已不易分辨,背风面旋涡尺寸明显增大,这说明桨尖拖出旋涡的强度得到了有效减弱。

|
图 10 基本外形和开槽桨尖外形的桨尖涡量等值线比较 Figure 10 Vorticity isoline comparison between basic square tip and slotted tip |
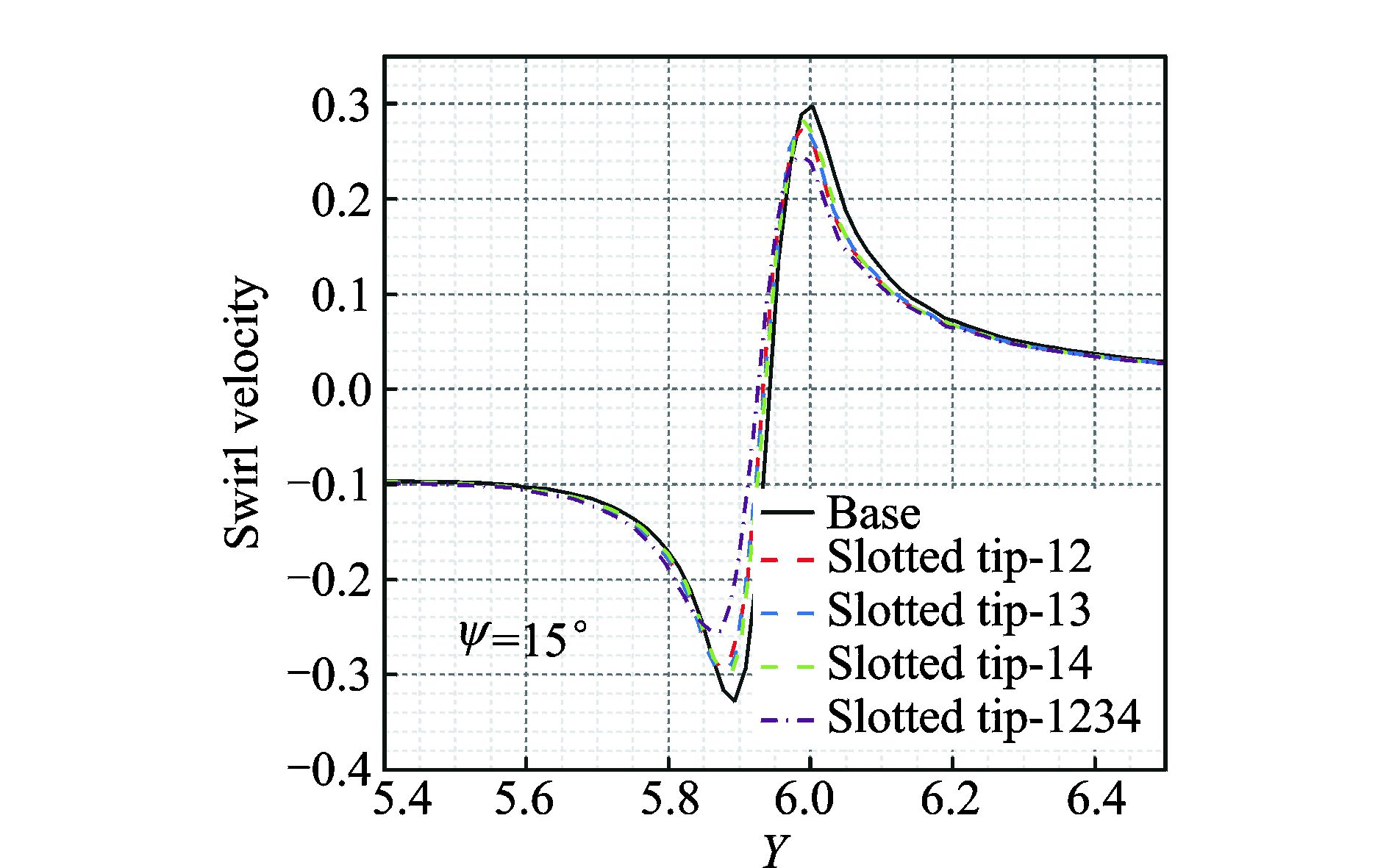
旋涡理论模型用拟合公式来表征旋涡的旋转速度、轴向速度和径向速度等,采用CFD数值模拟方法,旋涡的速度分布直接通过数值计算得到。对于旋翼桨尖涡来说,由封闭的涡面组成的管状涡面称为涡管,涡管的强度定义为绕涡管的一条封闭围线的环量,也就是说比较旋涡旋转速度的大小,就可以得到旋涡强度的大小关系。图 11给出了不同桨尖外形的桨尖涡旋转速度比较,其中周向截面对应的尾迹角ψ=15°,旋转速度用桨尖速度进行量纲化一。从图中可以看到,旋涡中心的旋转速度为0,两侧分别有1个符号相反的旋转速度峰值出现,涡心与出现峰值旋转速度之间的距离为涡核半径,在涡核半径以内,旋转速度沿径向增加;在涡核半径以外,旋转速度沿径向递减。由于桨尖拖出的旋涡处在悬停旋翼的下洗流场当中,涡心绝对速度(取两侧峰值旋转速度的平均值)并不为0。比较不同桨尖外形可以看到,基本外形的峰值旋转速度最大,四孔开槽桨尖的峰值旋转速度最小,3种两孔开槽桨尖的旋转速度分布比较一致,其峰值旋转速度介于基本外形和四孔开槽桨尖外形之间。从量值上看,以负方向的峰值旋转速度为例,两孔开槽桨尖外形在基本外形基础上峰值速度减小约9%,四孔开槽桨尖外形在基本外形基础上峰值速度减小约21%。
|
图 11 5种桨尖外形的桨尖涡旋转速度比较(尾迹角ψ=15°) Figure 11 Comparison of swirl velocities of five blade tips at ψ=15° |
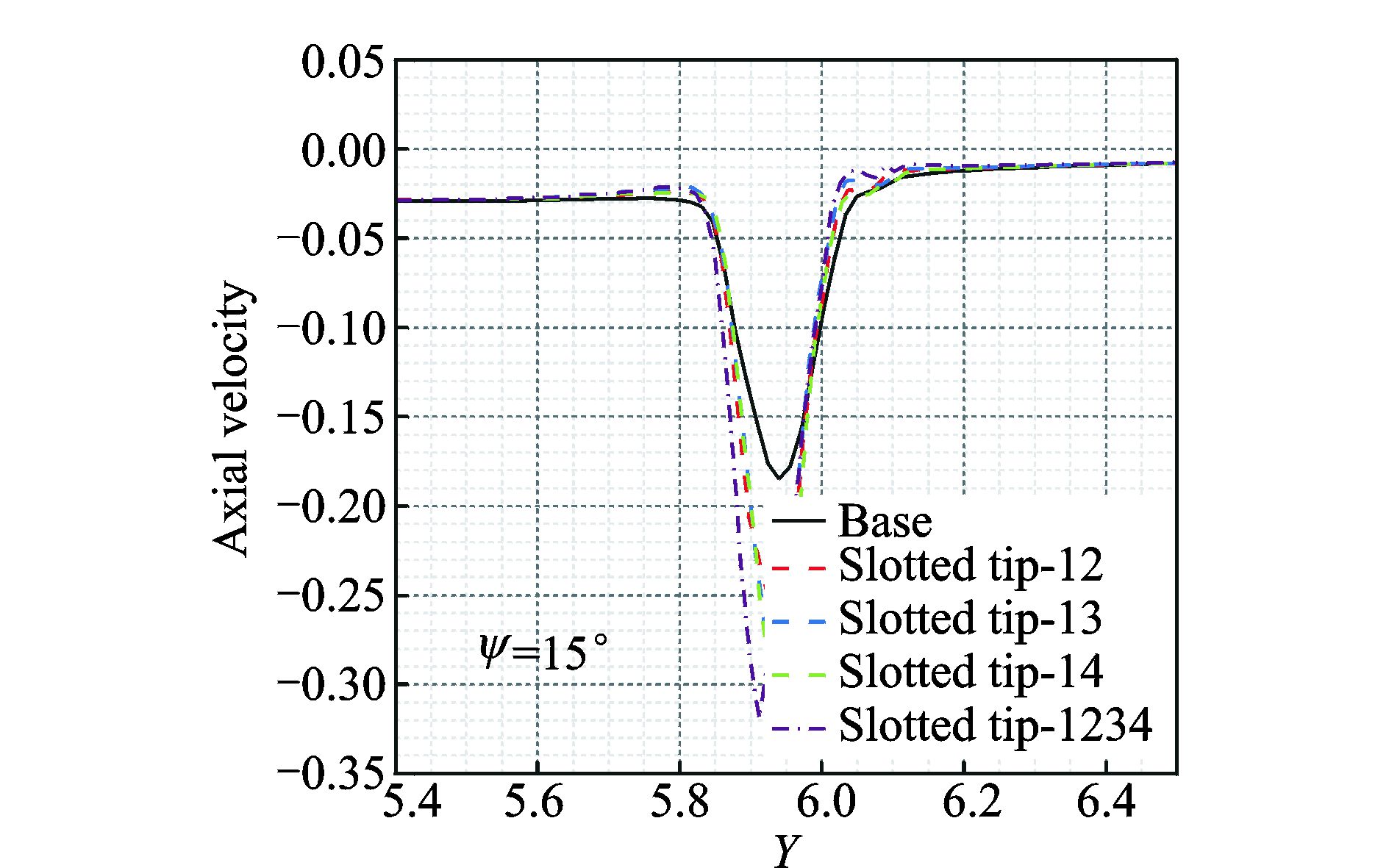
图 12给出了不同桨尖外形的桨尖涡轴向速度比较。关于轴向速度的产生可以理解为:沿桨尖涡的涡轴方向(涡轴连线称为涡线,是涡管当半径趋于无限小的极限),尾迹角越小对应的旋涡强度越大,涡心压力越小;尾迹角增大旋涡强度减弱、涡心压力增大,由于涡轴上的逆压梯度,就形成了沿涡轴反方向的流动速度。进一步说,旋涡的轴向速度峰值(绝对值)越大,对应沿涡轴方向的压力梯度越大,就说明桨尖涡的衰减程度越厉害。从图 12中可以看到,旋涡的轴向速度为负,就速度绝对值来说,基本外形对应的峰值轴向速度最小,四孔开槽桨尖对应的峰值速度最大,两孔开槽桨尖介于两者之间。定量来看,四孔开槽桨尖在基本外形基础上增大约74%,两孔开槽桨尖在基本外形基础上增大约32%~53%。
|
图 12 5种桨尖外形的桨尖涡轴向速度比较(尾迹角ψ=15°) Figure 12 Comparison of axial velocities of five blade tips at ψ=15° |
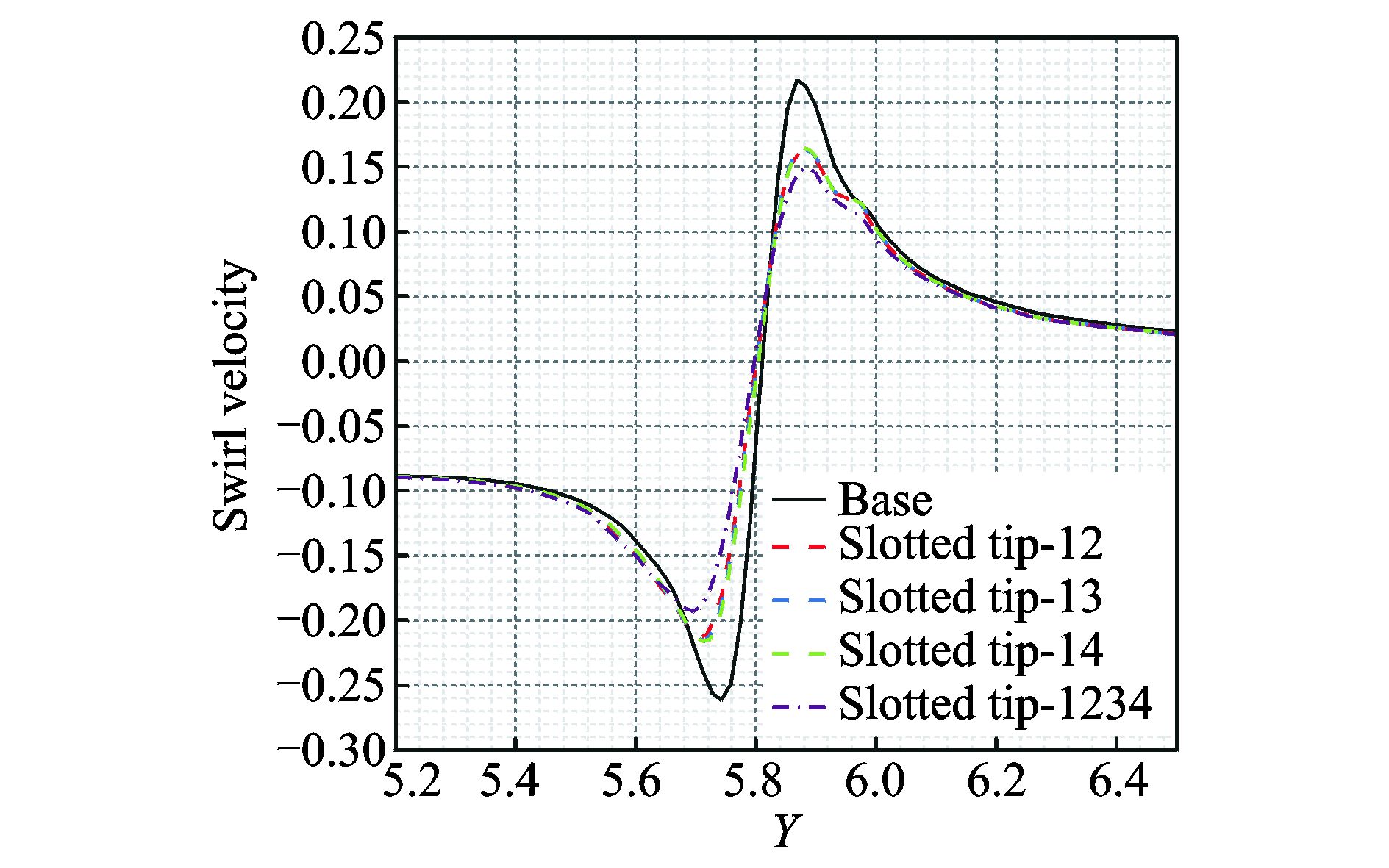
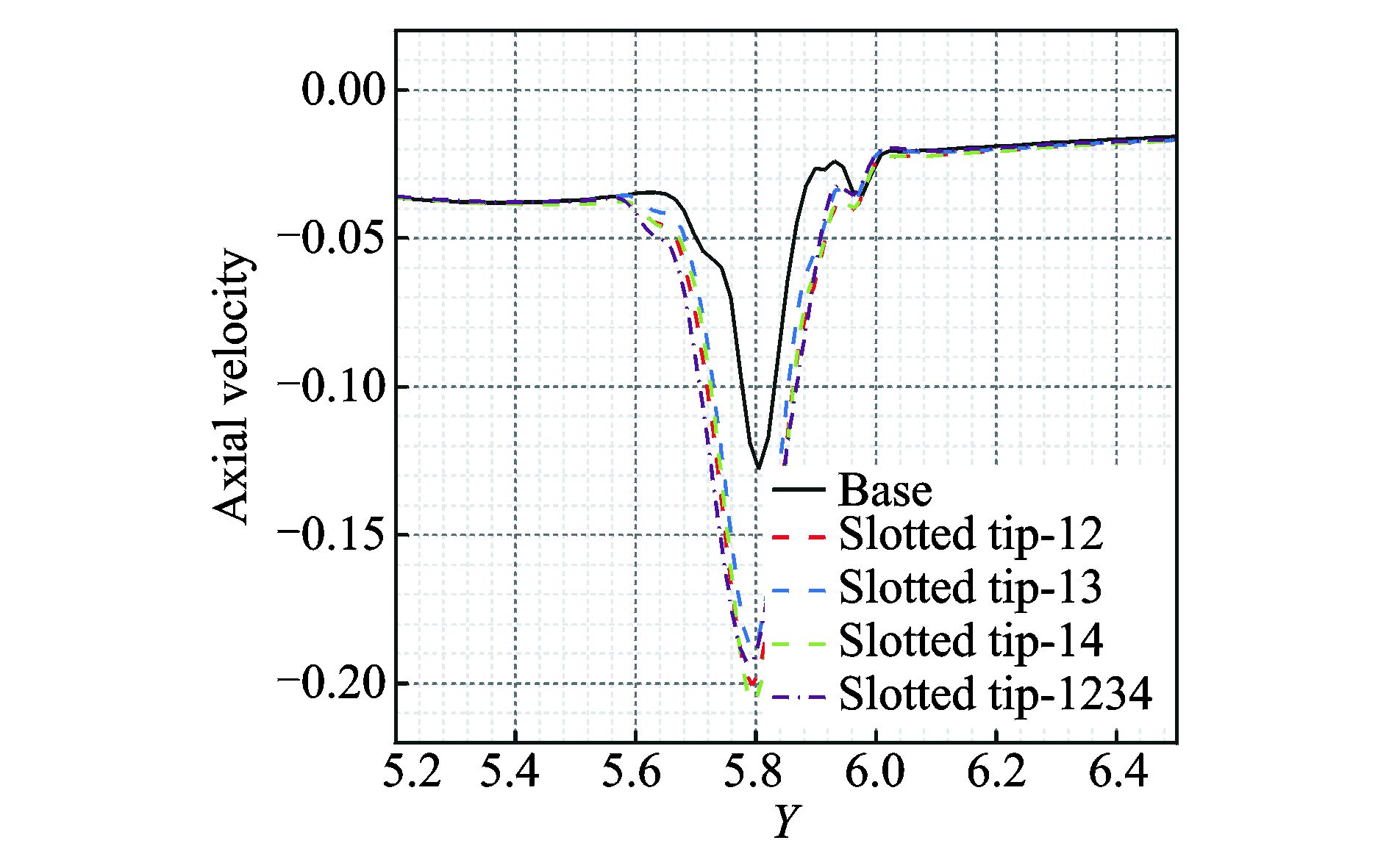
图 13给出了尾迹角ψ=45°下的桨尖涡旋转速度比较,可以看到此时旋涡的峰值旋转速度较前一截面(尾迹角ψ=15°)有所降低,受旋翼下洗流动的影响,涡心的平均速度向下,旋涡负方向的旋转速度峰值大于正方向。同样以负方向的峰值旋转速度为例,从量值上比较,两孔开槽桨尖外形在基本外形基础上峰值速度减小约15%,四孔开槽桨尖外形在基本外形基础上峰值速度减小约27%。图 14给出了尾迹角ψ=45°截面上的桨尖涡轴向速度比较,其中速度用桨尖速度量纲化一,从图中可以看到,基本外形的峰值轴向速度较小,开槽桨尖外形的峰值速度有显著的增加。与前一截面不同的是,此时四孔开槽桨尖与两孔开槽桨尖的差异已不明显,定量来看,开槽桨尖峰值轴向速度在基本外形基础上增大约52%~64%。
|
图 13 5种桨尖外形的桨尖涡旋转速度比较(尾迹角ψ=45°) Figure 13 Comparison of swirl velocities of five blade tips at ψ=45° |
|
图 14 5种桨尖外形的桨尖涡轴向速度比较(尾迹角ψ=45°) Figure 14 Comparison of axial velocities of five blade tips at ψ=45° |
|
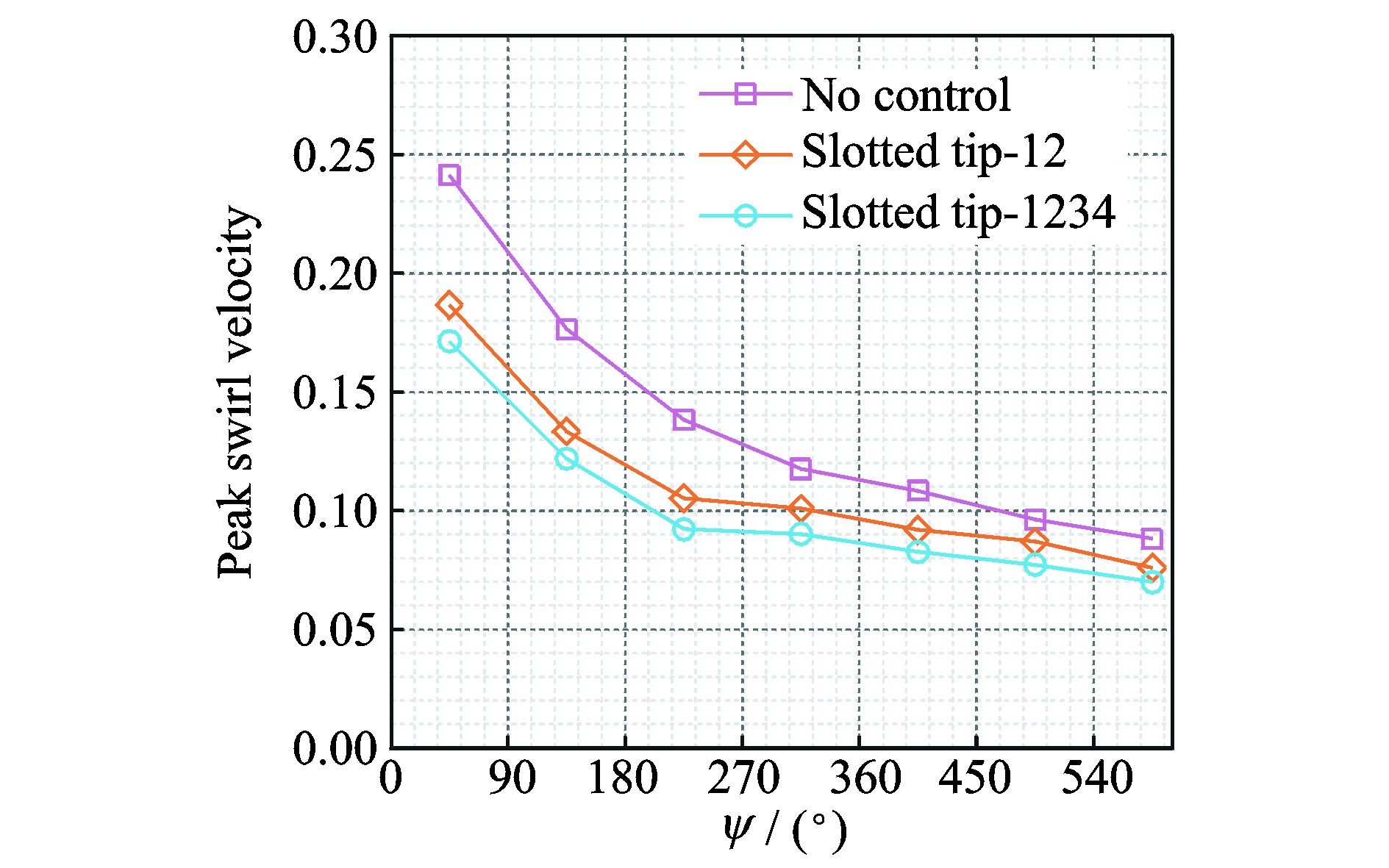
图 15 峰值旋转速度随尾迹角的变化 Figure 15 Distribution of peak swirl velocities by wake ages |
为了定量显示控制前后桨尖涡的发展演变,图 15给出了桨尖涡的峰值旋转速度随尾迹角的变化,其中峰值旋转速度由正负峰值旋转速度的绝对值平均得到,同时用桨尖旋转速度进行量纲化一。由于3种两孔模式开槽桨尖对桨尖涡的控制效果比较一致,图中只用了一种两孔模式(12孔)作为代表。从图中可以看到,随尾迹角增大,桨尖涡的峰值旋转速度减小,在尾迹角前180°内,峰值速度的下降速度尤为迅速,当尾迹角继续增大时,其下降速度趋于缓和。前面说到,桨尖涡的峰值旋转速度代表了旋涡的强度,对比3条曲线可以发现,两孔开槽桨尖的控制效果十分明显,桨尖涡强度比基本外形有了明显降低;四孔开槽桨尖在两孔基础上进一步降低了桨尖涡强度,但减小的幅度没有第1次明显。
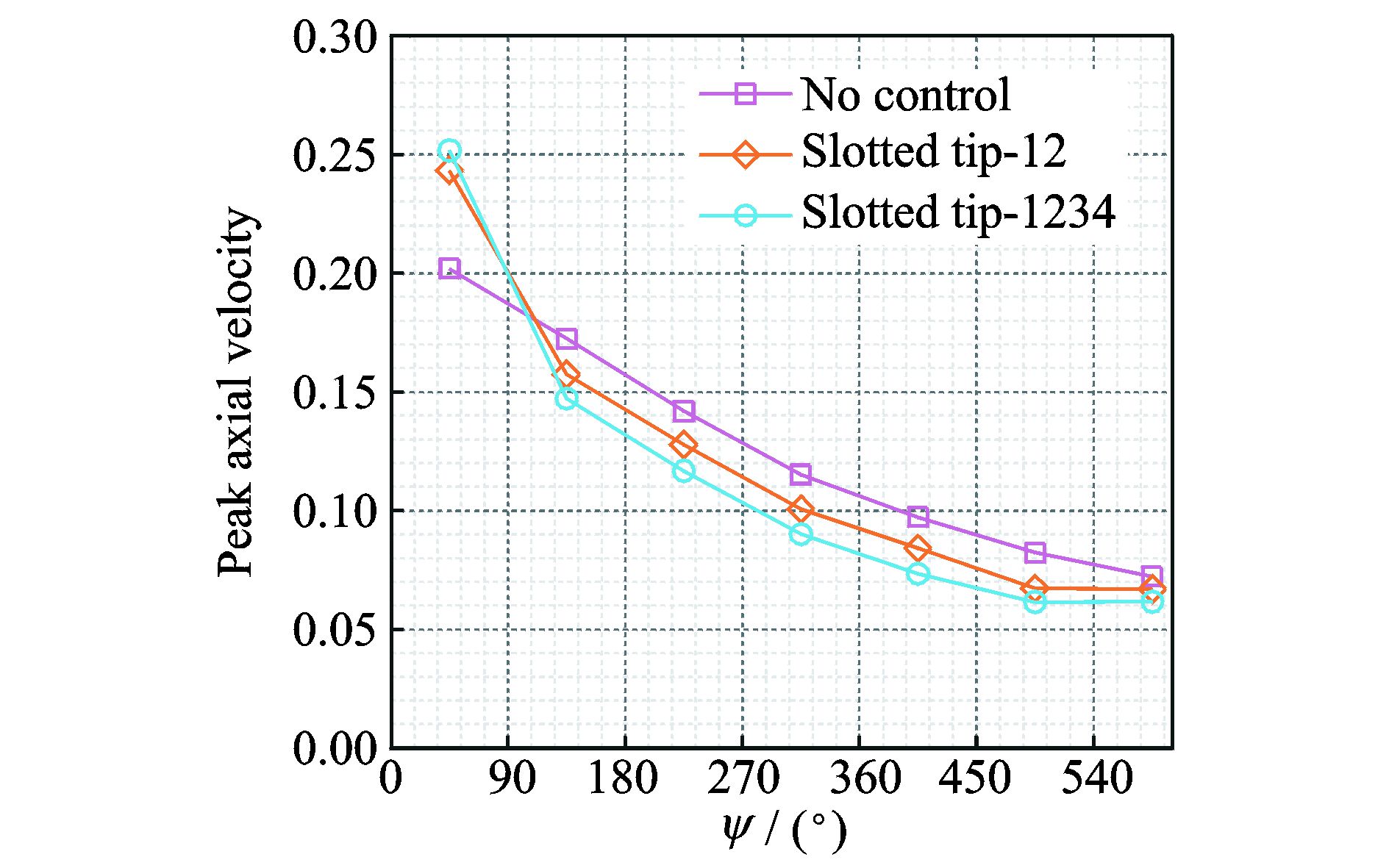
图 16给出了桨尖涡的峰值轴向速度随尾迹角的变化,其中速度用桨尖速度量纲化一。从图中可以看到,当尾迹角小于90°时,开槽桨尖外形的峰值轴向速度大于基本外形,由于涡心轴向速度一定程度上代表了涡线上的压力梯度,开槽桨尖的压力梯度大,说明桨尖涡的耗散较基本外形更大。当尾迹角大于90°时,开槽桨尖的变化曲线趋于缓和,和基本外形的变化趋势一致,在同一尾迹角下,其峰值轴向速度小于基本外形。就两孔与四孔开槽桨尖的比较来看,在尾迹角等于90°前后,四孔桨尖外形的峰值轴向速度先大后小,体现出了对桨尖涡更强的控制效果。
|
图 16 峰值轴向速度随尾迹角的变化 Figure 16 Distribution of peak axial velocities by wake ages |
表 1对基本外形和开槽桨尖外形的拉力与功率系数进行了比较,其中拉力系数CT=T/ρΩ2R2·πR2,同时给出了文献[12]中无控制桨尖的拉力系数试验值作为参考。从表中可以看到,当前计算的拉力系数值略大于试验值,但在合理的变化范围内,文献[13]采用拼接网格对同一状态进行了计算,得到的拉力系数为0.005 0,与本文计算值比较接近,一定程度验证了本文计算的合理性。增加开槽桨尖控制以后,桨叶的拉力系数在原外形基础上有轻微减小,桨叶的功率系数有所增加,其中3种两孔开槽桨尖的性能比较接近,四孔开槽桨尖比两孔的性能损失更大。从量值上看,两孔开槽桨尖的拉力系数较基本外形减小约1.2%,功率系数增大约2%~2.5%;四孔开槽桨尖的拉力系数较基本外形减小约2.2%,功率系数增大约5%。开槽桨尖导致旋翼性能降低的原因可以简单分析如下:由于在桨叶前缘增加开槽以后,导致这部分区域阻力增加,同时开槽位置靠近桨叶,距离旋转中心较远,因此对力矩的贡献较大。所以总的来说,开槽控制一方面减弱了桨尖涡的强度,另一方面带来拉力减小和扭矩增加的负面效应,在实用化之前,该流动控制技术还需要在开槽方式、位置等方面进行优化设计,以减弱对气动性能带来的不利影响。
| 表 1 5种桨尖外形的拉力与功率系数比较 Table 1 Comparison of thrust and power coefficients of five blade tips |
3 结论
通过以上数值研究,得到的主要结论如下:
(1) 本文所采用方法能够比较准确地模拟桨尖涡流动,开槽桨尖通过向桨尖涡内部注入横向流动,增强旋涡的掺混作用,能够有效减弱桨尖涡的强度,以尾迹角45°截面为例,两孔开槽桨尖使峰值旋转速度减小约15%,四孔开槽桨尖减小约27%,同时使峰值轴向速度明显增加。
(2) 开槽桨尖流动控制使悬停旋翼的拉力系数减小、扭矩系数增大。两孔开槽桨尖的拉力系数较基本外形减小约1.2%,功率系数增大约2%~2.5%;四孔开槽桨尖的拉力系数较基本外形减小约2.2%,功率系数增大约5%。
| [1] | Han Y O, Leishman J G. Investigation of helicopter rotor-blade-tip-vortex alleviation using a slotted tip[J]. AIAA Journal , 2004, 42 (3) : 524–535. DOI:10.2514/1.3254 |
| [2] | Bhagwat M J, Leishman J G. Generalized viscous vortex model for application to free-vortex wake and aeroacoustic calculations[C]//58th Annual Forum of the American Helicopter Society. Monteal, Canada:[s.n.], 2002: 58-2002-00078. |
| [3] | Han Y O. Diffused tip vortex structure generated by a slotted tip rotor blade[R]. AIAA Paper 2005-0057, 2005. |
| [4] | Zhong B, Qin N. Non-inertial multiblock Navier-Stokes calculation for hovering rotor flowfields using relative velocity approach[J]. Aeronautical Journal , 2001 : 379–389. |
| [5] |
陈义良.
物理流体力学[M]. 安徽: 中国科学技术大学出版社, 2008 .
Chen Yiliang. Physical fluid dynamics[M]. Anhui: University of Science and Technology of China, 2008 . |
| [6] |
肖中云, 江雄, 陈作斌, 等.
低速预处理方法在悬停旋翼模拟中的应用[J]. 航空学报 , 2008, 29 (2) : 321–326.
Xiao Zhongyun, Jiang Xiong, Chen Zuobin, et al. Application of low speed preconditioning to hover rotor simulation[J]. Aeronautical Jounal , 2008, 29 (2) : 321–326. |
| [7] |
牟斌, 肖中云, 周铸, 等.
直升机旋翼悬停流场的粘性数值模拟[J]. 空气动力学报 , 2009, 27 (5) : 582–585.
Mou Bin, Xiao Zhongyun, Zhou Zhu, et al. Numerical simulation of viscous flow-fields around helicopter rotor[J]. Jounal of Aerodynamics , 2009, 27 (5) : 582–585. |
| [8] | Spalart P. A one-equation turbulence model for aerodynamic flows[J]. Che La Recher Aérospatial , 1992, 439 (1) : 5–21. |
| [9] | Dacles-Mariani J, Zilliac G G, Chow J S, et al. Numerical/experimental study of a wingtip vortex in the near field[J]. AIAA Journal , 1995, 33 (9) : 1561–1568. DOI:10.2514/3.12826 |
| [10] | Vos J B, Leyland P. NSMB handbook 4.5[M]. Sweden: Dept of Aeronautics, KTH, 1999 . |
| [11] | Nichols R H. Turbulence models and their application to complex flows[M]. Birmingham: University of Alabama, 2010 . |
| [12] | Caradonna F X, Tung C. Experimental and analytical studies of a model helicopter rotor in hover[R]. NASA-TM-81232, 1981. |
| [13] |
孙威, 高正红, 黄江涛, 等.
旋转机翼悬停气动特性研究[J]. 空气动力学学报 , 2015, 33 (2) : 232–238.
Sun Wei, Gao Zhenghong, Huang Jiangtao, et al. Aerodynamic characteristics of hovering rotor/wing[J]. Acta Aerodynamics Sinica , 2015, 33 (2) : 232–238. |
 2016, Vol. 48
2016, Vol. 48


