在类似于舰船等对动力推动设备性能要求较高及其工作空间比较狭小的场合 ,具有脉宽调制(Pulse width modulation,PWM)变频器供电的感应电动机得到了广泛的应用[1-2]。但是,相对于无变频器供电的感应电动机拖动系统而言,电机的损耗特别是铁耗变化更为复杂,由此而引起的温升变化可能对电机工作性能或系统的安全运行形成威胁。因此,对PWM变频器供电的感应电动机内的传热特性研究具有一定的迫切性。
近年来,国内外的诸多专家学者分别采用有限元法[3-4] 和有限体积元法[5-6]对电机内损耗特性[7-8]及传热特性[9]进行了大量的研究。例如,在铁耗计算分析方面,文献[8]利用常系数三项式模型,计算分析了一台37 kW,4极异步电机铁耗,并通过热值试验对计算结果进行了验证;旋转磁化产生的损耗高于交变磁化所产生损耗,因此,文献[10]研究了铁心不同位置的磁化方式及其磁密变化特点对铁耗分布的影响。在传热特性方面,李伟力等以小型感应电机为例,采用有限元方法,对电机定子[11]及定转子全域[12]进行了二维温度场计算,分析了气隙温度和机壳表面散热翅的变化对定转子温升的影响;Xypteras将定转子之间的气隙作为一静止的导热介质,给出了相应的导热系数,将电机定转子二维温度场作为一个整体进行了联合求解[6];丁树业等采用有限体积法对大型核主泵屏蔽电机的三维温度场与流体场进行了耦合计算[5]。上述文献对电机温度场计算和分析中,仅对电机本体进行了分析,没有结合电机实际运行状况,考虑外控设备(变频器)的实际控制条件对电机内传热特性的影响。
本文以一台55 kW驱动用感应电机为例,基于流体力学及传热学基本原理,结合电机通风结构特征,在给定基本假设和边界条件基础上,建立外部包裹有空气域的三维流热耦合求解域模型,采用有限体积元法对脉宽调制PWM变频器供电下电机内温度场进行了数值研究,并得到了不同调制比控制条件下电机内的传热特性。通过搭建电机实验平台,进行温升测试实验,得到详细的实验数据。着重分析了PWM不同控制策略下电动机全域内各主要部件的温升分布特性,并与实验数据进行对比,验证了计算结果的准确性和求解方法的合理性。
1 数学模型 1.1 铁耗计算方程已有大量文献提出了多种铁耗计算模型,本文选用一种应用较广泛的模型,即Bertotti在文献[13]提出的常系数三项式模型,表达式如下
| $ {P_{fe}} = {k_h}f{B^2} + {k_e}{f^2}{B^2} + {k_c}{f^{1.5}}{B^{1.5}} $ | (1) |
式中:第1项为磁滞损耗;第2项为涡流损耗;第3项为附加损耗;kc,kh,ke为相应的耗系数,kh和ke可通过铁磁材料实测损耗数据拟合求得,ke=π2γd2/6ρ[13],其中:d为硅钢片厚度,m;ρ为硅钢片密度,kg/m3; f为基波频率,Hz;B为硅钢片的磁通密度,T。
1.2 流体控制方程流体流动受物理守恒定律的支配,电机内流体流动与传热满足质量、动量以及能量三大守恒定律,当流体为不可压缩且处于稳定流动状态时,相应的三维控制方程可简化表示为[14]
| $ div\left( {\rho u\phi } \right)div\left( {\Gamma {\rm{grad}}\phi } \right) + S $ | (2) |
式中:ø为通用变量;ρ为流体密度,kg/m3;Γ为扩展系数;S为广义源项。
1.3 三维热传导方程结合电机的材料特性以及数值传热学基本原理,在笛卡儿坐标系下,稳态温度场的合成方程为[14]
| $ \left. \begin{array}{l} \frac{{}}{x}\left( {{\lambda _x}\frac{T}{x}} \right) + \frac{{}}{y}\left( {{\lambda _y}\frac{T}{x}} \right) + \frac{{}}{z}\left( {{\lambda _z}\frac{T}{x}} \right) = - {q_v}\\ {\left. T \right|_{{S_1}}} = T\\ {\left. {\lambda \frac{T}{n}} \right|_{{S_2}}} = {T_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {x,y,z} \right) \in 绝热面\\ - \lambda \frac{T}{n} = \alpha \left( {T - {T_f}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {x,y,z} \right) \in 散热面{\kern 1pt} \end{array} \right| $ | (3) |
式中:T为物体边界面处求温度,K;λx,λy,λz为求解域内各种材料沿x,y以及z方向的导热系数,W/(mK);qv为求解域内各热源体密度之和,W/m3;S1,S2为物体某一恒温的边界;T0为物体边界面的温度值,K;α为散热表面的散热系数,W/( m2·K);Tf为散热面周围流体的温度,K。
2 求解模型及求解条件 2.1 电机的基本数据与损耗分布本文以PWM变频器供电的55 kW感应电动机为研究对象,对不同调制比控制条件下的电机内损耗分布特性进行研究,电机基本参数如表 1所示。
| 表 1 电机的基本参数 Table 1 Parameters of motor |
根据电机的基本参数及式(1),采用有限元法,分别对感应电机在 PWM变频参调制比M分别为0.8和0.9时的电磁场进行计算,得到相应的各部分损耗分布大小,如表 2所示。
| 表 2 M=0.8和M=0.9时电机主要部分损耗分布 Table 2 Loss distribution of motor at M=0.8 and M=0.9 |
从表 2对比分析可以看出,当调制比较小(M=0.8)时,电机的损耗相对较高,即热源密度较大,进而对电机的通风冷却能力提出更高的要求,因此电机温度场分析也尤为重要。
2.2 基本假设驱动感应电机内部结构复杂,转子端环上铸有扇叶,定子绕组为双层叠绕散下线,对于已建立的三维求解域物理模型,作出如下基本假设:
(1) 电机内流体流动时的雷诺数很大(Re > 2 300),属于紊流,故采用湍流模型对电机内的流场进行求解;
(2) 流体在电机内流动过程中,流速远小于声速(v < c),即马赫数很小,故把流体作为不可压缩流体处理;
(3) 涡流效应对每根线棒所产生的热量都是相同的,并且线棒端部用等效平直化的建模方式处理;
(4) 在电机稳定运行状态下,对电机内温度场及流体场进行研究,即控制方程中不含时间项。
2.3 通风结构本文中驱动用感应电机内流体流动情况复杂,电机外部采用强迫通风冷却系统,空气经风罩上网孔流入,在风扇旋转及风罩作用下,空气被压入电机散热翅风沟当中,带走机壳的热量;而在电机内部采用密闭结构,电机转子端环上铸有一定结构尺寸的扇叶,当转子转动时,扇叶被带动旋转,起到自励性风扇作用,更好地促进了电机内冷却介质与各主要部件之间的对流换热。
2.4 物理模型本文所研究的驱动用感应电机基本结构数据如表 3所示。
| 表 3 电机基本结构数据 Table 3 Basic structure data of motor |
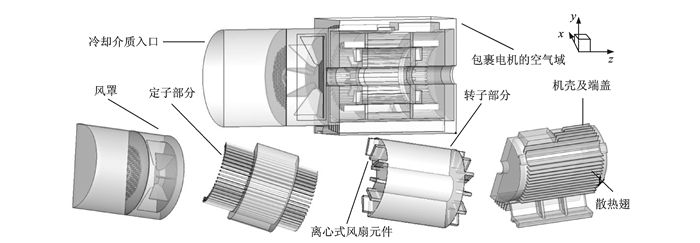
在基本假设的前提下,根据电机的结构特点及传热特性,确定求解域为电机整个轴向长度的半个圆周,建立电机外部有空气域包裹的流热耦合求解域模型,其结构示意图如图 1所示。
|
图 1 电机结构示意图 Figure 1 Physical model of motor structure |
电机求解域包括电机内部的转子导条、转子铁心、转子端部扇叶、定子绕组、定子铁心、散热翅、以及电机外部的自励离心式风扇及风罩。其中风罩入风孔采用实际建模方法,离心式风扇端部空气域进行加长处理,这样可以有效地避免回流现象产生。
2.5 边界条件根据电机通风结构及传热特性,认为电机外部风机与端部风罩接口处为冷却介质入口,包裹电机的外部空气域为出口,求解域内具体边界条件如下:
(1) 入口处采用压力入口边界条件,初始压强设置为一个标准大气压;
(2) 出口处采用压力出口边界条件,初始压强设置为一个标准大气压;
(3) 电机气隙两端采用周期性边界条件;
(4) 电机结构件与空气接触的面为散热面,求解域其他外边界为绝热面;
(5) 求解域内流体与固体接触面均认为无滑移边界面。
对于边界条件的设定,电机内各主要部件的材料特性如表 4所示。
| 表 4 电机内主要部件的材料特性 Table 4 Material properties of main components of motor |
3 实验测试及计算结果分析
本文中驱动用感应电机温升测试实验利用PT100温度传感器完成,实验初始环境温度为8.5 ℃,在电机稳定运行状态下,对定子绕组进行温升测量,采集不同时间点温升数值,得到有效的实验数据,实验现场测试装置如图 2所示。

|
图 2 电机温升实验装置示意图 Figure 2 View of experimental platform |
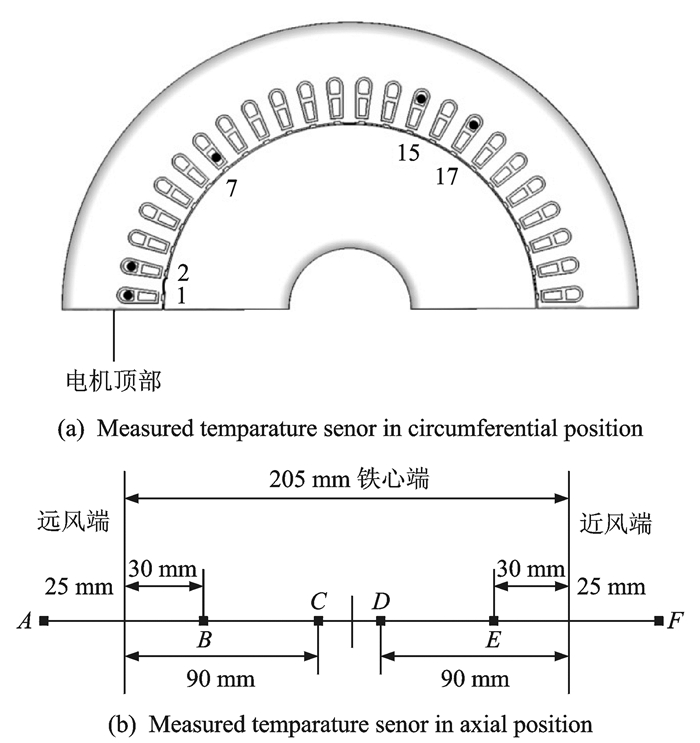
电机在变频参数M=0.8工作时,通过对物理模型进行温度场及流体场的强耦合求解,得到电机内主要部分温升分布情况。为了验证计算方法的正确性及所建模型的合理性,对电机定子绕组不同位置处的温升进行采集,并与仿真计算结果进行对比,其中仿真初始温度的设置为27 ℃,图 3给出了温度传感器测试点埋设位置的示意图。
|
图 3 温度传感器位置埋设示意图 Figure 3 Measured temperature sensor positions |
图 3(a,b)分别给出了PT100温度传感器沿周向及轴向的埋设位置。沿周向给定子绕组依次编号,靠近接线盒一侧的定子绕组编号为1,沿轴向从定子绕组远离电机端部离心式风扇一侧的远风端开始,取“A~F”点对定子绕组截面进行分析。其中传感器埋设在1号槽底部,靠近远风端铁心位置30 mm处,即“B”位置,则用“1-B”表示,其余位置可依次类推。
在实验过程中,采用PWM变频器对电机进行供电,每隔15 min采集一次数据,当同一PT100温度传感器相邻温升数值相差不超过0.4 K时,认为电机内温升达到稳定状态。表 5给出了电机内各传感器实验测得温升及软件仿真计算测得温升的对比情况。
| 表 5 温升实验测量值与仿真计算值对比 Table 5 Comparison of calculated temperamture-rise values with measured values |
由表 5可知,测温点当中最大和最小相对误差分别为6.70%和1.42%,温升计算结果与实测值基本吻合,满足了工程的实际需求,验证了数值计算结果的准确性及流热耦合求解方法的合理性。
3.1 不同调制比控制条件下电机整体温升分析通过对电机温度场进行流热耦合计算,得到由空气域包裹的电机内各部分温升分布情况。表 6给出了基于 PWM供电、不同调制比(M=0.8及M=0.9)控制条件下,电机内各主要部件的温升。
| 表 6 M=0.8和M=0.9时电机内各主要仿真部件温升 Table 6 Temperature-rise of main parts at M=0.8 and M=0.9 |
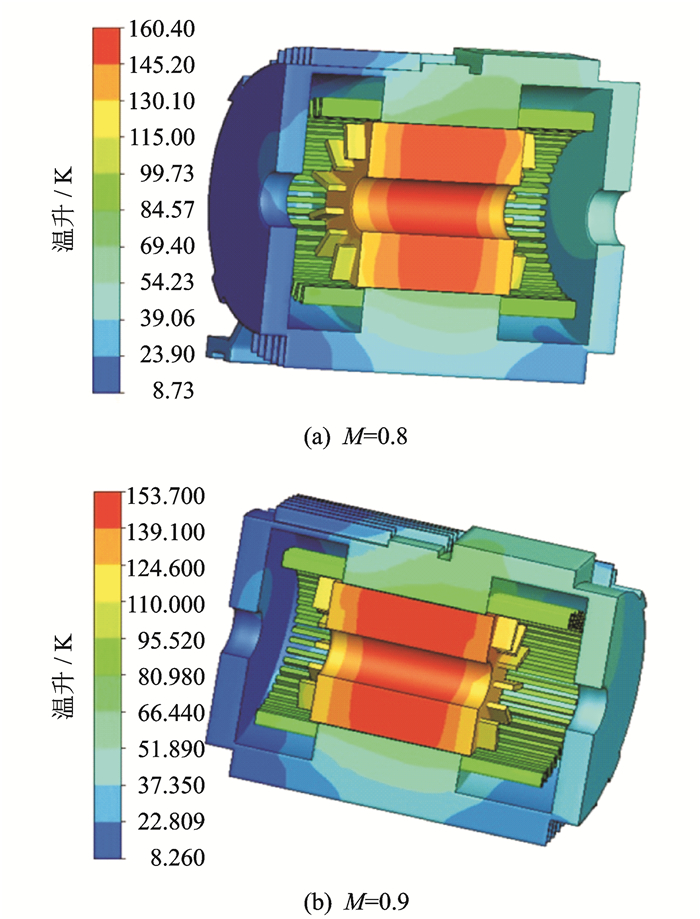
图 4给出了两个不同调制比控制条件下电机内主要部件温升分布云图,结合表 6可知:
|
图 4 电机整体温升 Figure 4 Temperature-rise distribution in motor |
(1) PWM变频参数分别为M=0.8和M=0.9时,电机内温升分布规律大致相同,定子各个部分平均温升相差不大,但转子各个部分平均温升相差较大,这是由于转子各部分均紧密接触 ,并处于电机径向中心位置,致使散热情况较差;
(2) M=0.8时,电机内各部分损耗较高,导致该情况下感应电机各主要部件温升较高,其最高温升(160.43 K)相比于M=0.9(153.72 K) 时高6.71 K,并且最高温升点都位于转子导条部分;
(3) 感应电机在调制比分别为M=0.8和M=0.9 控制条件下运行时,机壳部分温升最低,平均温升分别为37.26 K和36.06 K,相差仅为1 .20 K,这是因为机壳部分不是热源,又与外部流动的冷却空气接触,自然对流作用强,散热能力强,所以温升变化受损耗变化影响小。
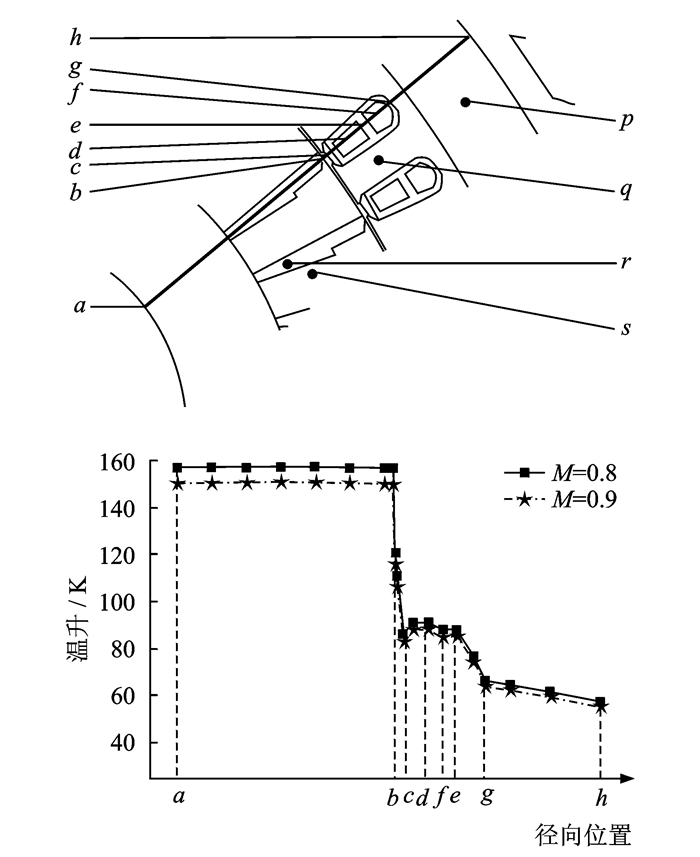
工况下,由于PWM变频参数不同,导致热源密度发生变化。为了详细研究电机内热传导情况,取求解域径向一条考察线,对比分析了两个不同调制比控制条件下电机内各部分温升分布特性,如图 5所示。从图 5及温度场计算结果可知:
|
图 5 两个不同调制比下电机径向温升曲线图 Figure 5 Curves of temperature-rise in radial direction under different modulation ratios |
(1) 电机内各部件温升变化规律一致,电机转子部分(ab段)两曲线温升接近,变化平缓,相对于其他部件温升较高,在转子径向外部,温升略有降低,这是因为定转子气隙间流动的空气与转子表面发生自然对流,将热量带走所致;
(2) 空气在定转子气隙间(bc段)流动,此处的紊流现象明显,空气温升较低,出现阶跃式变化;
(3) 定子部分(ch段)相对于转子部分(ab段)温升低,定子上层绕组(d处)温升相对于定子下层绕组(f处)高,而绝缘(e处)温升相对较低,这是因为绕组是热源,会产生相对较多的热量 ,但下层绕组靠近定子轭部,并处于径向外部,散热情况较好;
(4) 靠近下层定子绕组处绝缘(g处)温升变化明显,定子轭部(gh段)温升逐渐降低,且呈缓慢下降的趋势。
3.2 不同调制比控制条件下机壳温升分析电机定子部分与机壳直接接触,热传递作用强,机壳与外部冷却空气进行自然对流换热,散热情况较好,因此在电机内各个主要部件中机壳平均温升最低。
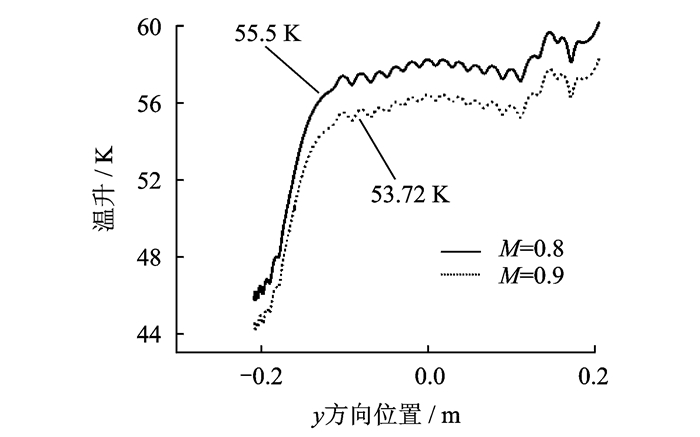
图 6给出了电机在两个不同调制比控制条件下机壳周向温升变化曲线,其中取线位置为径向206 mm 处,其平均温升分别为55.5,53.72 K。结合图 6及温度场计算结果可知:
|
图 6 不同调制比控制条件下机壳周向温升曲线图 Figure 6 Curves of temperature-rise in circumference direction under different modulation ratios |
(1) 两个不同调制比控制条件下机壳温升变化趋势一致,M=0.8时机壳最高温升(60.75 K)与M=0.9时机壳最高温升(58.80 K)相差1.95 K;
(2) 周向上看,底部到顶部温升逐渐升高,是因为底部风量无损失,散热情况较好,温升较低,机壳侧面散热翅对电机散热作用效果明显,温升呈波浪式变化;而电机顶部位置,由于吊装部件及接线盒对冷却空气流动的阻碍作用,温升较高;
(3) 散热翅近风端温升较低,是因为空气由风罩刚进入机壳散热翅风沟时,空气温度低,流量大,且散热翅扰流作用明显,导致冷却空气流动速度发生畸变,使对流换热能力增强。
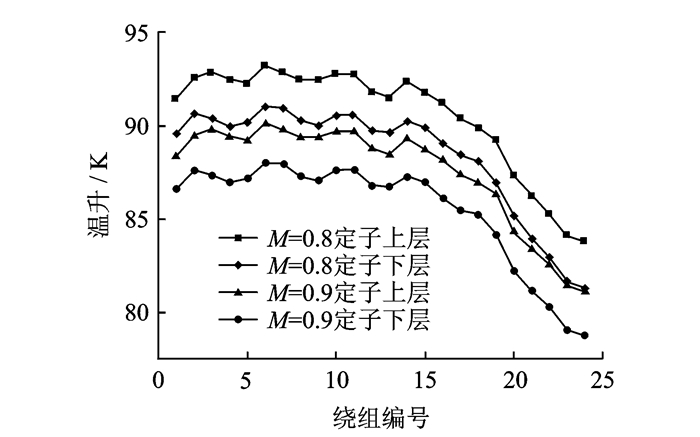
3.3 不同调制比控制条件下定子温升分析为了更好地对比不同调制比控制条件下电机内定子绕组部分温升分布特性,图 7给出了定子上、下层绕组温升变化曲线,从电机顶部到底部依次将定子绕组进行编号1~24。根据图 7及温度场计算结果可以看出:
|
图 7 不同调制比控制条件下定子上下层绕组温升曲线图 Figure 7 Curves of temperature-rise of stator winding under different modulation ratios |
(1) 周向上看,上、下层绕组温升变化趋势大致相同,温升最高位置为定子绕组上端部分,即靠近电机接线盒处,这是因为电机接线盒及吊装环对外风路冷却空气有阻碍作用,使电机冷却空气在其位置处风量损失严重,接线盒处的冷却能力下降,热量流通不畅;
(2) 靠近电机顶部及侧面位置定子绕组平均温升呈波浪式变化,而靠近电机底部位置绕组平均温升变化剧烈,近似呈线性下降,到电机底部位置温升降低变缓;
(3) 上层绕组1 号和3号曲线的平均温升分别为90.6 K和87.6 K,下层绕组2号和4号曲线的平均温升分别为88.4 K和85.5 K,因此在两个不同调制比控制条件下,定子上、下层绕组平均温升相差3 K左右。
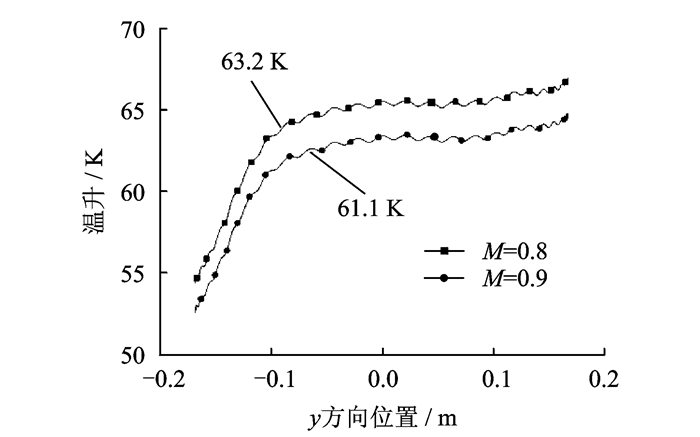
图 8给出了不同调制比控制条件下电机定子轭部周向温升变化曲线,其中取线位置为定子轭部径向168 mm处,其平均温升分别为63.2 K及61.1 K。从图 8可以看出:
|
图 8 不同调制比控制条件下定子轭部周向温升曲线图 Figure 8 Curves of temperature-rise of stator yoke in circumference direction under different modulation ratios |
(1) 周向上看,定子轭部温升变化趋势与定子绕组及机壳周向温升变化趋势大致相同,且温升变化平缓,电机顶部与接线盒相对应位置的温升较高;
(2) 定子轭部温升变化在周向上呈波浪式变化,这是因为散热翅对电机定子轭部散热作用,说明机壳上散热翅的结构设计对电机温升影响的重要性;
(3) 由于机壳支座阻碍冷却空气流动,导致与支座相对应的定子轭部位置散热情况较差,温升较高,而与电机底部对应的定子轭部位置温升较低,因此这两部分进行热传递,温升曲线呈近似线性变化。
由于接线盒对外风路的阻碍作用,致使接线盒附近空气的冷却能力下降,而定子铁心与机壳直接接触,因此对定子铁心温升分布特性的研究尤为重要。
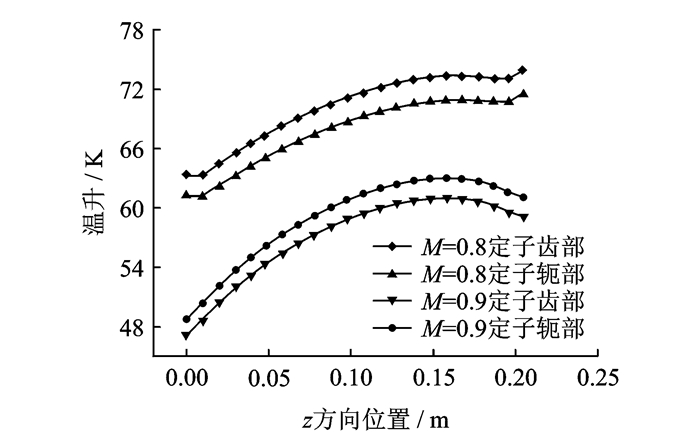
图 9给出了不同调制比控制条件下电机定子齿部及轭部轴向温升变化曲线,其中取线位置如图 5中p点(定子轭部 )及q点(定子齿部)。从图 9中可以看出:
|
图 9 不同调制比控制条件下定子齿部和轭部轴向温升曲线图 Figure 9 Curves of temperature-rise of tooth and yoke of stator in axial direction under different modulation ratios |
(1) 两个不同调制比控制条件下,定子轭部与齿部温升变化趋势分别大致相同,温升变化趋势平缓;
(2) 轴向上看,定子轭部最高温升点位于轴向中心靠近远风端处,两端温升较低,且近风端温升较远风端低,而定子齿部随着轴向长度的增长,温升逐渐升高,最高温升位于远风端一侧的端部。
3.4 不同调制比控制条件下转子温升分析由电机整体温升分布云图 4可知,PWM变频器供电下驱动用感应电机转子部分整体温升较高,因此对转子温升分布特性的分析很有意义。图 10给出了不同调制比控制条件下转子导条及铁心轴向温升变化曲线。 根据图 10及温度场计算结果可知,由于转子两端与转子端环紧密接触,当转轴转动时,端环上的扇叶元件也随之带动气腔内空气高速流动旋转,使转子两端散热加快,因此转子部分两端温升较低,最高温升位于轴向中心段;由于转子导条与铁心紧密接触,因此转子导条与转子铁心轴向温升变化趋势一致,温升大致相同。
|
图 10 不同调制比控制条件下转子导条及转子铁心轴向温升曲线图 Figure 10 Curves of temperature-rise of bar and core of rotor in axial direction under different modulation ratios |
4 结论
本文以一台基于55 kW感应电机为例,建立了三维物理模型求解域,采用有限体积法,在PWM控制下分别对变频参数分别为M=0.8和M=0.9时电机的传热特性进行了分析,对电机内各主要部件的温升分布情况进行了对比分析,得出相应结论:
(1) 感应电动机的温升计算结果与实验结果相吻合,满足了工程实际需求;
(2) 两个不同调制比控制条件下电机求解域内各主要部件温升分布趋势大致相同,最高温升点未发生偏移,定子部分温升数值相接近,转子部分各个位置温升值相差较大;
(3) 径向上,转子部分温升较高,转子导条与铁心温升数值相近,在气隙位置温升出现阶跃式变化,定子部分温升较低;轴向上,电机各部分近风端温升较低,远风端温升较高;周向上,定子铁心轭部与机壳直接接触,散热翅散热作用在电机定子轭部体现明显,温升呈波浪式变化。
| [1] |
寿海明, 冀路明, 马守军. 现代船用推进电机技术研究. 船电技术[J], 2007 (1)
:36–39.
Shou Haiming, Ji Luming, Ma Shoujun. Research on modern marine propulsion motor technology. Marine Electric & Electric Technology[J], 2007 (1) :36–39 . |
| [2] | Fang Wei, Liu Xiaodong, Liu Yanfei. Optimalcontrol strategy for buck converter under successive load current change. Transactions of Nanjing University of Aeronautics & Astronautics[J], 2014, 31 (6) :530–537 . |
| [3] |
曹君慈, 李伟力, 程树康, 等. 复合笼条转子感应电动机温度场计算及相关性分析. 中国电机工程学报[J], 2008,28 (30)
:96–103.
Cao Junci, Li Weili, Cheng Shukang, et al. Temperature field calculation and associated factor analysis of induction motor with compound cage rotor. Proceedings of the CESS[J], 2008, 28 (30) :96–103 . |
| [4] | Liu Y J, Lee Y, Jung H K, et al. 3D thermalstress analysis of the rotor of an induction motor. IEEE Transactions on Magnetic[J], 2000, 36 (4) :1394–1397 . |
| [5] |
丁树业, 孟凡东, 葛云中. 核主泵屏蔽电机温度场研究. 中国电机工程学报[J], 2012,32 (36)
:149–155.
Ding Shuye, Meng Fandong, Ge Yunzhong. Temperature field investigation of canned primary pump motors in nuclear power stations. Proceedings of the CSEE[J], 2012, 32 (36) :149–155 . |
| [6] | Xypteras J, Hatziathanassiou V. Thermal analysis of an electrical machine taking into account the iron losses and the deep-bar effect. IEEE Transactions on Energy Conversion[J], 1999, 14 (4) :996–1003 . |
| [7] |
丁树业, 李冠男, 冯海军, 等. 驱动用异步电机负载变化对损耗影响数值计算. 电机与控制学报[J], 2013,17 (9)
:36–41.
Ding Shuye, Li Guannan, Feng Haijun, et al. Numerical calculation of loss under load variation for driving asynchronous motor. Electric Machines and Control[J], 2013, 17 (9) :36–41 . |
| [8] | Mueller M A, Williamson S, Flack T J, et al.Calculation of iron losses from time-stepped finite-element models of cage induction machines [C] //Seventh International Conference on Electric Machines and Drives Conference. Anterbury, UK: [s.n.], 1995: 88-92. |
| [9] |
陶文铨.
数值传热学[M]. 西安: 西安交通大学出版社, 2001 : 347 -353.
Tao Wenquan. Numerical heat transfer[M]. Xi′an: Xi′an Jiaotong University Press, 2001 : 347 -353. |
| [10] |
赵海森, 罗应立, 刘晓芳, 等. 异步电机空载铁耗分布的时步有限元分析. 中国电机工程学报[J], 2010,30 (30)
:99–106.
Zhao Haishen, Luo Yingli, Luo Xiaofang, et al. Analysis on no-load iron losses distribution of asynchronous motor with time-stepping finite element method. Proceedings of the CSEE[J], 2010, 30 (30) :99–106 . |
| [11] |
靳延船, 李伟力, 李守法. 感应电机定子温度场的数值计算. 电机与控制学报[J], 2006,10 (5)
:492–497.
Jin Yanchuan, Li Weili, Li Shoufa. Numerica1 calculation and analysis of stator thermal field in a induction machine. Electric Machines and Control[J], 2006, 10 (5) :492–497 . |
| [12] |
李伟力, 李守法, 谢颖, 等. 感应电动机定转子全域温度场数值计算及相关因素敏感性分析. 中国电机工程学报[J], 2004,27 (24)
:85–91.
Li Weili, Li Shoufa, Xie Ying, et al. Stator-rotor coupled thermal field numerical calculation of induction motors and correlated factors sensitivity analysis. Proceedings of the CSEE[J], 2004, 27 (24) :85–91 . |
| [13] | Bertotti G. General properties of power losses in soft ferromagnetic material. IEEE Transactions on Magnetics[J], 1988, 24 (1) :621–630 . |
| [14] |
丁树业, 郭保成, 冯海军, 等. 变频控制下永磁同步电机温度场分析. 中国电机工程学报[J], 2014,34 (9)
:1369–1375.
Ding Shuye, Guo Baocheng, Feng Haijun, et al. Temperature field investigation of permanent magnet synchronous motors controlled by the frequency conversion control system. Proceedings of the CSEE[J], 2014, 34 (9) :1369–1375 . |
 2016, Vol. 48
2016, Vol. 48


