南京航空航天大学江苏省精密与微细制造技术重点实验室, 南京, 210016
收稿日期: 2014-09-29; 修订日期: 2015-11-25
基金项目: 国家自然科学基金(51575256)资助项目;江苏省自然科学基金(BK2012798)资助项目;江苏省产学研联合创新基金——前瞻性联合研究(BK2013003-10)资助项目。
Jiangsu Key Laboratory of Precision and Micro-manufacturing Technology,Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China
自然界中微生物在低雷诺数液体环境下的运动为微型游动机器人的研发注入了灵感[1],对鞭毛菌等单细胞生物的运动形式及机理的研究与仿生设计成为热点[2-4]。微型游动机器人的结构尺寸微小、器件精密,能够进入到人类和宏观机器人所不及的狭窄空间进行微细定位和微细操作,比如:微型管道机器人可用于煤气、化工及发电设备中细小管道的探伤和维护;医用微型机器人能够进入人体内腔进行医疗检测和微创手术;特殊作业微型机器人则面向复杂机械系统的非拆卸检修。因此,微型游动机器人的应用前景十分广阔。
作者课题组在对鞭毛运动机理分析研究的基础上,研制了一种仿生机器人。机器人运动实验表明,当靠近壁面运动时,机器人将出现规律性转向。这种现象的发生必然与其仿生原理密切相关。为此,有必要对机器人的仿生对象——鞭毛菌在壁面附近的运动行为进行研究,以进一步提高鞭毛游动的仿生应用水平。
当前,关于鞭毛菌在壁面附近的运动行为的研究,主要围绕3个方面进行:(1)鞭毛菌的运动轨迹。Berg和Turner[5]发现,大肠杆菌(Escherichia coli,E.coli)在靠近物体表面时,受壁面的影响会沿圆形轨迹向前游动。Lauga等[6]通过对不同时刻细菌的运动图像的叠加,成功获得了完整的圆周轨迹,并基于抗力理论对该现象的运动机理进行阐释。Goto等[7]则建立了单鞭毛菌的近壁运动模型,对其前进与后退运动轨迹中表现出的不对称现象进行了研究。(2)鞭毛菌的运动速度。最早Reynolds[8]基于Taylor[9]的二维波动板简化模型,探讨了壁面的存在对鞭毛菌运动速度的影响。其后Ramia[10]利用边界元(Boundary element method,BEM)思想分析获得了鞭毛菌周围流体的速度场,并得出结论:细菌的运动速度随着与壁面之间距离的减小而减小。Frymier[11]利用跟踪显微镜记录了鞭毛菌在壁面附近的运动,其实验结论与Ramia模型的理论结果十分吻合。Goto等[12]在对单鞭毛菌的近壁运动进行实验观测和理论建模后也发现了同样的运动规律。(3)鞭毛菌与壁面之间的流体作用。Berke等 [13]在对E.coli于限定环境下的分布密度进行测量后发现,细菌在壁面附近的积聚行为显著增加,由此分析得出壁面对鞭毛菌具有引力作用并给出了相关的理论证明。Shum等[14]则对鞭毛菌的几何形状对该流体作用的影响进行了讨论。
根据已有的研究成果可知,壁面对鞭毛菌运动的影响是多方面的,其中之一便是细菌游动速度的减小。微型机器人的运动过程中,需要规避或利用这种效应,实现仿生机器人的精确控制。为此,需对鞭毛菌的游动速度减小的机理进行更为系统的分析。
本文利用抗力理论建立近壁环境下的鞭毛菌水动力模型,并对该模型的正确性进行验证。在此基础上,重点分析细菌鞭毛的几何及运动学参数对其游动速度的影响,为仿鞭毛游动的微型机器人运动控制提供参考依据。
1 鞭毛菌的运动描述
自然界中的鞭毛菌按鞭毛的数目及其生长部位,可分为单毛菌、双毛菌、丛毛菌和周毛菌。其中,周毛菌周身都分布有鞭毛,其运动特性涵盖了其他种类的鞭毛菌。为此,本文选取大肠杆菌E.coli作为研究对象,对该周毛菌的运动行为进行分析。
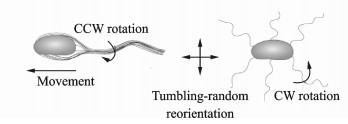
E.coli的鞭毛呈螺旋状,由嵌入在其细胞壁内的鞭毛马达带动旋转,产生推进力驱动细菌游动,如图 1所示。从鞭毛尾末端观测,当鞭毛马达逆时针(Counter-clockwise,CCW)旋转时,螺旋尾会绑定成一束,形成方向相同的推进力,细菌因此向前游动;当鞭毛马达向顺时针 (Clockwise,CW)方向旋转时,鞭毛束解开,螺旋尾产生不同方向的作用力,细菌原地翻转,从而导致运动方向发生改变。鞭毛菌通常沿直线前进运动,并通过间歇性的翻转以改变运动方向,实现对目标的逐渐接近。
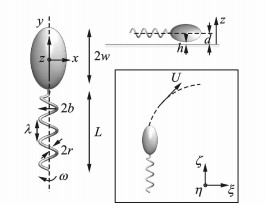
为便于分析和计算,以规则的椭球体代替鞭毛菌的头部,并将前进运动中绑定成束的鞭毛尾看成刚性整体,建立如图 2所示的简化模型。其中,从尾部末端观测,螺旋尾相对于细菌头部作逆时针旋转。表 1所示为描述鞭毛菌运动的相关参数定义。
表 1(Table 1)

表 1 鞭毛菌描述参数列表
Table 1 List of symbols and their meanings
| 符号 |
含义 |
| U |
鞭毛菌的运动线速度,U=(Ux,Uy,Uz) |
| Ω |
鞭毛菌的转动角速度,Ω=(Ωx,Ωy,Ωz) |
| U |
鞭毛菌在xoy平面内的运动速度 |
| ω |
螺旋尾相对于鞭毛菌头部的旋转速度 |
| Ω′ |
螺旋尾的角速度,Ω′=(Ωx,(Ωy-ω),Ωz) |
| μ |
液体的动力粘度系数 |
| w,φ |
椭球形头部的半长轴大小及其纵横比 |
| a |
与椭球体等价的球半径 |
| d |
鞭毛菌质心距离壁面的高度 |
| h |
鞭毛菌与壁面之间的间隙厚度 |
| b,λ |
螺旋尾的半径和波长 |
| n |
螺旋尾的整波个数 |
| r |
鞭毛丝的半径 |
| L |
螺旋尾的长度,L=nλ |
| Fw,Lw |
Fw=(Fwx,Fwy,Fwz),Lw=(Lwx,Lwy,Lwz) |
| Fh,Lh |
Fh=(Fhx,Fhy,Fhz),Lh=(Lhx,Lhy,Lhz) |
| Ft,Lt |
Ft=(Ftx,Fty,Ftz),Lt=(Ltx,Lty,Ltz) |
| F,L |
F=(Fx,Fy,Fz),L=(Lx,Ly,Lz) |
| un,ut |
微元的法向速度和切向速度 |
| δFn,δFt |
流体作用于微元的正压力和切向阻力 |
| ct,cn |
切向阻力系数和正压力系数 |
| ε |
鞭毛丝的细长比,ε=2πb/λ |
|
表 1 鞭毛菌描述参数列表
Table 1 List of symbols and their meanings
|
鞭毛菌等微生物在低雷诺数液体环境中运动,相比于粘性力,惯性力的影响基本可以忽略,即细菌仅受粘滞阻力Fw和粘滞力矩Lw的作用。若忽略细菌头部和尾部之间的流体相互作用,则
|
$
{{F}_{w}}={{F}_{\text{h}}}+{{F}_{\text{t}}}
$
|
(1) |
|
$
{{L}_{w}}={{L}_{\text{h}}}+{{L}_{\text{t}}}
$
|
(2) |
式中:Fh和Lh分别为流体作用于鞭毛菌头部的粘滞阻力和粘滞力矩;Ft和Lt则表示作用于鞭毛菌尾部的粘滞阻力和粘滞力矩。鞭毛菌在远离壁面运动时,螺旋尾旋转产生的推进力和转动力矩分别与流体作用其上的Fw和Lw平衡。因此,它在沿自身轴线向前运动的同时绕该轴作逆时针旋转,即
|
$
U={{U}_{y}}{{e}_{y}},\Omega ={{\Omega }_{y}}{{e}_{y\ \ \ }}
$
|
(3) |
式中:Uy>0且Ωy>0。而当鞭毛菌做近壁运动时,由于壁面影响,靠近壁面处的粘滞阻力较大,造成流体对细菌头部及螺旋鞭毛束的上下表面作用力不同,从而导致细菌运动轨迹和速度的改变。
2 鞭毛菌头部的流体作用
N-S方程是描述粘性不可压缩流体的运动方程,微观条件下可被简化为Stokes方程。Stokes方程表明,作用在鞭毛菌不同部位上的粘滞阻力和粘滞力矩与该部位的运动线速度和转动角速度线性相关。于是鞭毛菌头部的受力可表示为
|
$
\left| \begin{matrix}
{{F}_{\text{h}}}^{\text{T}} \\
{{L}_{\text{h}}}^{\text{T}} \\
\end{matrix} \right|={{M}_{\text{h}}}\left| \begin{matrix}
{{U}^{\text{T}}} \\
{{\Omega }^{\text{T}}} \\
\end{matrix} \right|
$
|
(4) |
式中:Mh为6×6的粘性系数矩阵。
将粘性系数标记为Xijαβ,当上标αβ取为FU时,它表示粘滞阻力F的i方向分量与其运动线速度U的j方向分量的线性关系,即
|
$
{{F}_{i}}=X_{ij}^{FU}{{U}_{j}}
$
|
同理,αβ取下列值时该系数有如下含义:FΩ——粘滞阻力与角速度的线性关系;LU——粘滞力矩与线速度的线性关系;LΩ——粘滞力矩与角速度的线性关系。并且,当表示与鞭毛菌头部相关的粘性系数时,X为N或V,其中,Vijαβ在鞭毛菌远离壁面游动时,取值为零,而Nijαβ则在任何情况下均不为零。于是Mh可表示为
|
$
\begin{matrix}
{{M}_{\text{h}}}= \\
\left| \begin{matrix}
-N_{xx}^{FU}\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ V_{xy}^{F\Omega }\ \ \ 0 \\
\begin{matrix}
0\ \ \ -N_{yy}^{FU}\ \ \ 0\ \ -V_{yx}^{F\Omega }\ \ \ 0\ \ \ 0 \\
0\ \ \ \ 0\ \ \ \ -N_{zz}^{FU}\ \ \ \ 0\ \ \ \ \ 0\ \ \ \ 0 \\
\begin{matrix}
0\ \ \ -N_{xy}^{VU}\ \ 0\ \ \ -N_{xx}^{L\Omega }\ \ \ 0\ \ \ 0 \\
V_{yx}^{LU}\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ -N_{yy}^{L\Omega }\ \ \ 0 \\
0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ -N_{zz}^{L\Omega } \\
\end{matrix} \\
\end{matrix} \\
\end{matrix} \right| \\
\end{matrix}
$
|
鞭毛菌头部近似为椭球形,可通过式(5)简化为半径为a的球体。
|
$
\frac{\alpha }{w}=\frac{4}{3}\frac{1}{\frac{2{{\varphi }^{2}}-1}{\sqrt{{{\varphi }^{2}}-1}}\ln \left| \frac{\varphi +\sqrt{{{\varphi }^{2}}-1}}{\varphi -\sqrt{{{\varphi }^{2}}-1}} \right|-\frac{2{{\varphi }^{2}}}{{{\varphi }^{2}}-1}}
$
|
(15) |
由于$ h\ll a $,应用润滑理论可得到Mh中的粘性系数[15-17]为
|
$
N_{xx}^{FU}=N_{yy}^{FU}=6\pi \mu \alpha \left[ \frac{8}{15}\ln \left( \frac{a}{h} \right)+0.96 \right]
$
|
(6a) |
|
$
N_{zz}^{FU}=6\pi \mu \frac{{{\alpha }^{2}}}{h}
$
|
(6b) |
|
$
N_{xx}^{L\Omega }=N_{yy}^{L\Omega }=8\pi \mu \alpha \left[ \frac{2}{5}\ln \left( \frac{a}{h} \right)+0.38 \right]
$
|
(6c) |
|
$
N_{zz}^{L\Omega }=8\pi \mu {{\alpha }^{3}}
$
|
(6d) |
|
$
V_{xy}^{F\Omega }=V_{yx}^{F\Omega }=6\pi \mu {{\alpha }^{2}}\left[ \frac{2}{15}\ln \left( \frac{a}{h} \right)-0.25 \right]
$
|
(6e) |
|
$
V_{xy}^{LU}=V_{yx}^{LU}=8\pi \mu {{\alpha }^{2}}\left[ \frac{1}{10}\ln \left( \frac{a}{h} \right)-0.19 \right]
$
|
(6f) |
3 鞭毛菌尾部的流体作用
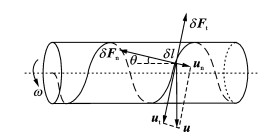
3.1 螺旋尾的旋进游动描述模型 根据抗力理论,将螺旋状鞭毛分割为若干微元,并取其中长为δl的一段,当螺旋尾以一定的角频率旋转时,该微元的速度可分解为图 3所示的法向速度分量un和切向速度分量ut。因此,每段微元受到周围流体对其施加的两种力的作用:正压力δFn和切向阻力δFt。力的大小分别与法向和切向速度成正比,方向则与其相反,即
|
$
\delta {{F}_{\text{n}}}=-{{\delta }_{l}}{{c}_{\text{n}}}{{u}_{\text{n}}},\delta F=-{{\delta }_{l}}{{c}_{\text{t}}}{{u}_{\text{t}}}
$
|
(7) |
将上述两种力合成,得到微元所受流体作用力
|
$
\delta F=\delta {{F}_{\text{n}}}+\delta {{F}_{\text{t}}}=-{{\delta }_{l}}\left( {{c}_{\text{n}}}{{u}_{\text{n}}}+{{c}_{\text{t}}}{{u}_{\text{t}}} \right)
$
|
(8) |
式中切向阻力系数和正压力系数分别为[18]
|
$
{{c}_{\text{t}}}=\frac{2\pi \mu }{\ln \left( \frac{2\lambda }{r} \right)-\frac{1}{2}},{{c}_{\text{n}}}=2{{c}_{\text{t}}}
$
|
当螺旋尾位于壁面附近时,该系数应修正为[19]
|
$
{{c}_{\text{t}}}=\frac{2\pi \mu }{\ln \left( \frac{2d\left( z \right)}{r} \right)-\frac{1}{2}},{{c}_{\text{n}}}=2{{c}_{\text{t}}}
$
|
式中:d(z)表示鞭毛微元距离壁面的高度,取值范围从d-b到d+b。
由于螺旋结构的特殊性,当鞭毛尾仅做围绕中心轴线旋转时,其上所有微元的运动完全一致。于是,流体对整个螺旋鞭毛尾的作用可通过各个微元受到的流体力δF的叠加得到。
3.2 鞭毛菌尾部的受力计算
根据Stokes方程,鞭毛菌尾部的受力可表示为
|
$
\left| \begin{matrix}
{{F}_{\text{t}}}^{\text{T}} \\
{{L}_{\text{h}}}^{\text{T}} \\
\end{matrix} \right|={{M}_{\text{t}}}\left| \begin{matrix}
{{U}^{\text{T}}} \\
{{\Omega }^{\text{T}}} \\
\end{matrix} \right|
$
|
(9) |
式中
|
$
\begin{matrix}
{{M}_{\text{t}}}= \\
\left| \begin{matrix}
\begin{matrix}
-M_{xx}^{FU}\ \ \ W_{xy}^{FU}\ \ \ 0\ \ \ M_{xx}^{F\Omega }\ \ \ W_{xy}^{F\Omega }\ \ \ -M_{xz}^{F\Omega } \\
W_{yx}^{FU}\ \ \ -M_{yy}^{FU}\ \ \ 0\ \ \ -W_{yx}^{F\Omega }\ \ \ -M_{yy}^{F\Omega }\ \ \ W_{yz}^{F\Omega } \\
\end{matrix} \\
0\ \ \ \ \ 0\ \ \ \ \ -M_{zz}^{FU}\ \ \ \ M_{zx}^{F\Omega }\ \ \ \ \ 0\ \ \ \ \ M_{zz}^{F\Omega } \\
\begin{matrix}
\begin{matrix}
M_{xx}^{LU}\ \ \ -W_{xy}^{LU}\ \ \ M_{zx}^{LU}\ \ \ -M_{xx}^{L\Omega }\ \ \ -W_{xy}^{L\Omega }\ \ \ 0 \\
W_{yx}^{LU}\ \ \ -M_{yy}^{LU}\ \ \ 0\ \ \ -W_{yx}^{L\Omega }\ \ \ -M_{yy}^{L\Omega }\ \ \ -W_{yz}^{L\Omega } \\
\end{matrix} \\
-M_{zx}^{LU}\ \ \ W_{zy}^{LU}\ \ \ M_{zz}^{LU}\ \ \ 0\ \ \ W_{zy}^{L\Omega }\ \ \ -M_{zz}^{L\Omega } \\
\end{matrix} \\
\end{matrix} \right| \\
\end{matrix}
$
|
其中Mijαβ和Wijαβ是与鞭毛菌尾部相关的粘性参数,并且Wijαβ在鞭毛菌远离壁面游动时取值为零,而Mijαβ则在任何情况下均不为零。
鞭毛菌的螺旋尾的几何模型可表述为
|
$
\left\{ \begin{matrix}
x=b\sin \left( s-\omega t \right) \\
y=-\frac{\lambda }{2\pi }\left( s+{{s}_{0}} \right) \\
z=b\cos \left( s-\omega t \right) \\
\end{matrix} \right.\ \ \ \ \ s\in \left[ 0,2n\text{ }\!\!\pi\!\!\text{ } \right]
$
|
(10) |
式中:s为鞭毛丝上各点的曲线坐标。
依据抗力理论,Mt中的粘性系数分别为
|
$
M_{xx}^{FU}=M_{zz}^{FU}=2{{c}_{\text{t}}}L\frac{1+3{{\varepsilon }^{2}}/4}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}
$
|
(11a) |
|
$
M_{yy}^{FU}={{c}_{\text{t}}}L\frac{1+2{{\varepsilon }^{2}}}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}
$
|
(11b) |
|
$
M_{yy}^{FU}=M_{yy}^{F\Omega }={{c}_{\text{t}}}bL\frac{\varepsilon }{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}
$
|
(11c) |
|
$
M_{xx}^{L\Omega }=M_{zz}^{L\Omega }=\frac{2}{3}{{c}_{\text{t}}}{{L}^{3}}\frac{1+3{{\varepsilon }^{2}}/4}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}
$
|
(11d) |
|
$
M_{zx}^{F\Omega }=M_{xz}^{F\Omega }=M_{xz}^{LU}=M_{zx}^{LU}={{c}_{\text{t}}}{{L}^{2}}\frac{1+3{{\varepsilon }^{2}}/4}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}
$
|
(11e) |
|
$
M_{yy}^{L\Omega }=2{{c}_{\text{t}}}{{b}^{2}}L\frac{1+{{\varepsilon }^{2}}/2}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}
$
|
(11f) |
|
$
M_{xx}^{LU}=M_{zz}^{LU}=M_{xx}^{F\Omega }=M_{zz}^{F\Omega }={{c}_{\text{t}}}bL\frac{{{\varepsilon }^{2}}/2}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}
$
|
(11g) |
|
$
W_{yx}^{LU}=W_{xy}^{F\Omega }=-2{{c}_{\text{t}}}bL\frac{1+{{\varepsilon }^{2}}/2}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}T
$
|
(11h) |
|
$
W_{xy}^{FU}=W_{yx}^{FU}=-{{c}_{\text{t}}}L\frac{\varepsilon }{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}T
$
|
(11i) |
|
$
W_{zy}^{LU}=W_{yz}^{F\Omega }=-{{c}_{\text{t}}}{{L}^{2}}\frac{\varepsilon }{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}\Gamma
$
|
(11j) |
|
$
W_{xy}^{LU}=W_{yx}^{F\Omega }=-{{c}_{\text{t}}}b{{L}^{2}}\frac{1+2{{\varepsilon }^{2}}}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}\Gamma
$
|
(11k) |
|
$
W_{zy}^{L\Omega }=W_{yz}^{L\Omega }=-2{{c}_{\text{t}}}b{{L}^{2}}\frac{1+{{\varepsilon }^{2}}/2}{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}\Gamma
$
|
(11l) |
|
$
W_{xy}^{L\Omega }=W_{yx}^{L\Omega }=-{{c}_{\text{t}}}bL\frac{\varepsilon }{{{\left( 1+{{\varepsilon }^{2}} \right)}^{1/2}}}\Gamma
$
|
(11m) |
式中:ct表示当鞭毛菌距离壁面的高度为d时,切向阻力系数ct的值;Τ和Γ则代表两个积分量
|
$
\Gamma =_{0}^{1}\cos \left( 2\pi u \right)f\left( \cos \left( 2\pi u \right) \right)\text{d}u
$
|
|
$
\Gamma =_{0}^{1}\left( u+{{u}_{0}} \right)\cos \left( 2\pi nu \right)f\left( \cos \left( 2\pi nu \right) \right)\text{d}u
$
|
4 基于理论模型的运动仿真
4.1 鞭毛菌动力学方程
为更好地对鞭毛菌的运动参量进行描述,需建立两种坐标系,位于其质心处的体坐标系Oxyz,以及与大地固结的惯性坐标系Eξηζ,如图 2所示。
由广义欧拉角定义可知,体坐标系要达到一个相对惯性坐标系的新姿态,需要通过3次旋转变换,于是两个坐标之间的转换方程为
|
$
\left[ x\ \ y\ \ z \right]=R\cdot \left[ \xi \ \ \eta \ \ \zeta \right]\
$
|
(12) |
|
$
R=\left| \begin{matrix}
\cos \psi \cos \theta \ \ \ \cos \psi \cos \theta \sin \varphi -\sin \psi cos\varphi \ \ \cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi \ \ \\
\sin \psi \cos \theta \ \ \ \sin \psi sin\theta \sin \varphi +\cos \psi cos\varphi \ \ \sin \psi \sin \theta \cos \varphi +\cos \psi \sin \varphi \\
-\sin \theta \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cos \theta \sin \varphi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cos \theta \cos \varphi \\
\end{matrix} \right|
$
|
根据牛顿-欧拉方程,鞭毛菌的动力学方程可以写成
|
$
m\left( \dot{U}+\Omega \times U \right)={{F}_{w}}
$
|
(13) |
|
$
\left( I\cdot \dot{\Omega }+\Omega \times I\cdot \Omega \right)={{L}_{w}}
$
|
(14) |
式中:Fw和Lw为整个鞭毛菌受到的粘滞阻力和粘滞力矩,分别由式(1,2)给出;I为鞭毛菌惯性矩阵,表达式如下
|
$
I=\left| \begin{matrix}
{{I}_{x}}\ \ \ 0\ \ \ 0 \\
0\ \ \ {{I}_{y}}\ \ \ 0 \\
0\ \ \ 0\ \ \ {{I}_{z}} \\
\end{matrix} \right|
$
|
E.coli鞭毛菌的主要参数如表 2所示[14]。将表 2中的主要参数值输入所建动力学模型,可计算得到细菌的速度与角速度变量。在此基础上,通过积分并在式(12)的转换下可最终获得细菌在惯性坐标系中的近壁运动时的质心轨迹曲线。
表 2(Table 2)

表 2 E.coil鞭毛菌的主要参数列表
Table 2 Main parameters of E.coil
| 参数 |
参数值 |
|
μ/(N·S·m-2) |
0.001 |
|
λ/μm |
2.5 |
|
b/nm |
250 |
|
h/nm |
10 |
|
n
|
3 |
|
r/nm |
50 |
|
w/μm |
2.5 |
|
φ
|
1.67 |
|
m/kg |
10-12 |
|
ω/(rad·s-1) |
980 |
|
Ix,Iz/(kg·m-2) |
0.93×10-27 |
|
Iy/(kg·m-2) |
0.205×10-27 |
|
表 2 E.coil鞭毛菌的主要参数列表
Table 2 Main parameters of E.coil
|
4.2 实验数据与模型仿真结果对比
图 4所示为鞭毛菌在平行于壁面的平面内的运动轨迹,其中图 4(a)为实际摄得的鞭毛菌近壁运动轨迹的影像叠加图[6];图 4(b)为初始速度设定为零时,通过理论模型仿真得到的鞭毛菌的质心运动轨迹。将图 4(a,b)进行对比可以发现,基于模型的运动轨迹仿真结果与实际轨迹变化趋势一致,即鞭毛菌在壁面的作用下将不再沿直线前进,而是绕圆周向前运动。
图 5为鞭毛菌的运动速度随距壁高度的变化图。其中,鞭毛菌的游动速度和距壁高度分别采用无量纲参数U/U∞和h/a进行描述,而U∞表示细菌远离壁面时的游动速度。图中,实心圆形散点所示为Frymier对细菌运动实验观测所得数据[20];空心菱形散点所示为依据动力学模型计算得到的结果;实线则是Ramia的BEM法分析所得数据的拟合曲线[10]。三者呈现出相似的规律,即鞭毛菌在壁面附近游动时,其运动速度会减小,且越靠近壁面,速度变化越明显。这进一步证明了本文所建理论模型的正确性。此外,相比于Ramia的分析结果[10],本文的仿真数据与实验结果之间的偏差虽然较大,但BEM法针对不同形状尺寸的鞭毛菌需要划分不同的边界单元,操作不易、计算繁复,且作为一种数值方法,它无法获得细菌周围流场的解析解。因而,本文的动力学模型应用更为广泛。
4.3 近壁运动时速度影响因素仿真分析
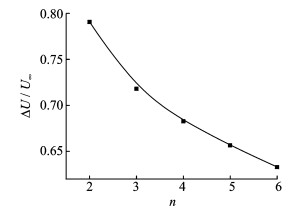
本文研究结果表明:所建立的动力学模型能很好地模拟近壁效应。实际的细菌在壁面附近运动时,除了距壁高度外,运动速度所受影响因素很多,为实现仿生机器人在壁面附近的有效控制,需要对细菌近壁运动时的影响因素做更深入的探讨。本节利用4.1节建立的动力学模型进行仿真分析。仿真计算采用控制变量法进行,全部参数的初值设定见表 2,对其中某一参数进行仿真时,只需改变该参数的值。壁面对速度的影响作用则通过鞭毛菌近壁运动时h=10 nm速度的减小量ΔU与其远离壁面时h=∞的运动速度U∞的比值ΔU/U∞来表示,其中,ΔU=U∞-U。图 6~10所示为细菌速度减小量随鞭毛尾几何及运动学参数的变化曲线图。
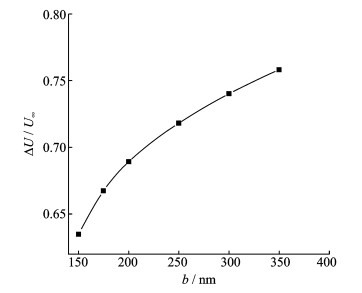
图 6所示为螺旋尾直径与鞭毛菌近壁运动速度变化关系图。由图 6可知,螺旋直径越大,鞭毛菌的运动速度下降得就越多,表明壁面对其运动速度的影响越显著。不过随着b值的增大,ΔU/U∞的变化趋于平缓,这说明螺旋直径对鞭毛菌速度变化的影响将逐渐减弱。
图 7所示为螺旋尾的整波个数与鞭毛菌近壁运动速度变化的关系图。从图 7中可以看出,壁面对细菌运动速度的作用会随着整波数目的增多而减小。
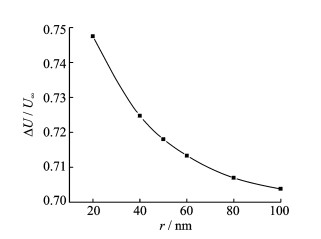
图 8所示为鞭毛丝半径与细菌近壁运动速度变化的关系图。由图 8可知,壁面对鞭毛菌运动速度的影响随着鞭毛丝半径的增大而减弱。然而从纵坐标ΔU/U∞的变化范围可以看出,鞭毛丝半径对速度变化的影响并不明显。
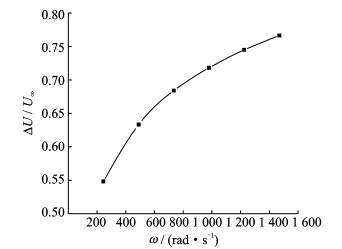
图 9所示为螺旋尾角速度与鞭毛菌近壁运动速度关系图。将其与图 6进行对比可以发现,鞭毛尾旋转速度的影响作用与其螺旋直径的作用类似,即旋转速度越大,运动速度的减小越明显。但同时随着角速度的不断增大,这种影响作用将越来越弱。
图 10所示为螺旋尾波长与鞭毛菌近壁运动速度变化关系图。图 10中显示,细菌运动速度的减小量随波长的增大快速上升,大致在λ/2b=π,即鞭毛尾螺旋升角为45°时到达顶点,之后开始缓慢下降。故而当鞭毛尾螺旋升角在45°左右,壁面对细菌运动速度的影响最大。
5 结论
鞭毛菌在近壁环境下游动时,其运动行为显示出一定特殊性,针对这一现象,本文做了以下工作:
(1) 根据鞭毛菌在液体中游动时的结构特点和运动特性,提出了E.coli细菌的简化模型。在此基础上,利用抗力理论和Stokes方程对鞭毛菌在壁面附近运动时流体对其施加的作用力进行了分析。
(2) 基于牛顿-欧拉方程建立了鞭毛菌近壁运动的动力学模型。通过对细菌在平行于壁面平面内的运动轨迹与游动速度的计算和与实验数据的对比分析,验证了模型的有效性。
(3) 对螺旋尾的几何和运动学参数对近壁运动速度变化的影响进行了探讨,发现:壁面对细菌运动速度的作用会因螺旋半径、旋转速度的增大和整波个数、鞭毛半径的减小而增强,并在螺旋升角为45°左右时达到最大。
由于细菌实际是依靠其柔性鞭毛尾的波形推动来运动的,与本文的刚性尾简化模型的推进原理有所不同,后续的研究工作将集中于建立鞭毛菌的柔性尾模型以更好地模拟细菌的实际运动。本文的研究将为微型仿生游动机器人在如何规避近壁效应及如何有效地实现运动控制提供参考数据。



 2016, Vol. 48
2016, Vol. 48


