近年来,高强度淬硬钢材料在汽车工业中被应用的比例不断增加[1]。能否对这些难加工材料进行高效加工直接影响中国汽车行业的发展。淬硬钢其硬度高达58~63 HRC,是典型的难加工的材料。相对于球头刀点接触窄行加工形式,使用周边切削刃与底面切削刃之间以一小段圆弧过渡的环形铣刀加工淬硬钢时,可以极大地增加切削平稳性,提高加工精度、表面质量和切削效率[2]。在刀具的设计和制造中,刀刃曲线的设计和刃磨加工至关重要,因为刀刃不仅决定了刀具的外形,而且对刀具的切削性能、加工质量起着重要作用[3-4]。在环形铣刀的圆角回转面设计方面,许多学者提出了不同的圆角回转面设计方法。如鲍青山等通过回转面的刃口曲线通式公式推导出了圆角回转面的表达式[5];唐余勇等建立了带圆角铣刀的回转面曲线方程,并且根据在与经线成定角定义下的刃口曲线求解公式,直接由刀具回转面方程求出带角圆的凸弧铣刀上角圆回转面方程[6-7]。
本文为了精确磨制环形铣刀,从回转刀具刃线出发,根据广义螺旋运动概念,建立了环形铣刀周刃与圆角刃的等螺旋角数学模型,并依据刃线模型得到环形铣刀的磨削轨迹,从而为环形铣刀数控刃磨加工提供理论依据和指导。
1 环形铣刀的应用目前典型的数控铣削刀具主要有球头铣刀、平头端铣刀及环形铣刀等,如图 1所示 。其中环形铣刀越来越多地被应用在汽车覆盖件模具钢的加工中。

|
图 1 数控铣削的常用刀具 Figure 1 Frequently-used tool in NC milling process |
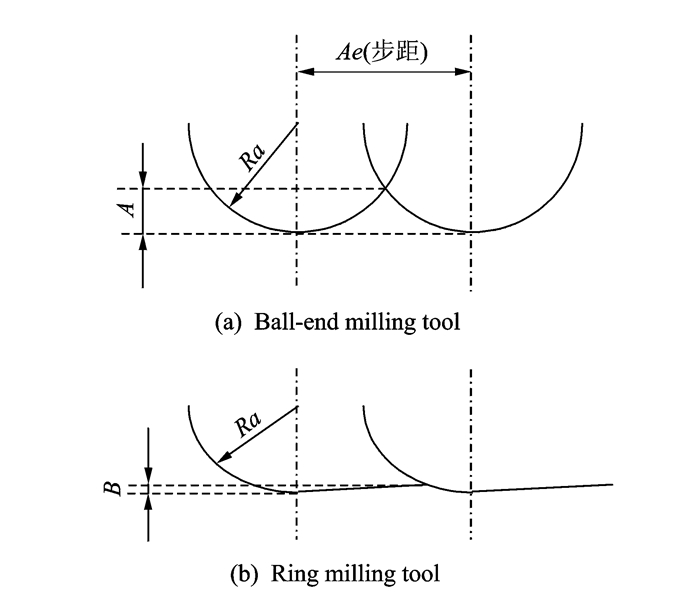
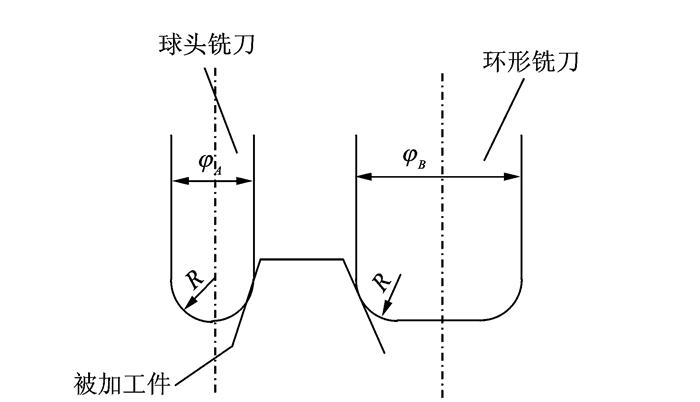
球头铣刀在切削过程中,球头刀的底部为球形 ,因此具有自适应性(即刀具的法截线曲率半径恒为刀具半径)。这种自适应性使刀具的行距与干涉避免的计算都大为简化。但其缺点是容屑空间小、底部切削效率低及切削速度不恒定,球头铣刀的切削刃在不同位置处的切削速度不同,而且在接近球头端点处的切削速度为零。正是这些局限性导致了球头刀加工效率与表面质量难以提高。从几何学形状来看,环形铣刀和球头铣刀相比在加工面的表面粗糙度上具有明显的优势。如果在获得同样高的加工残余量理论高度(即获取同样的表面粗糙度)的前提下,与球头铣刀相比,环形铣刀的步距要宽数倍,所以可大大地缩短加工时间[8],如图 2所示。另外,如果同样只是需要刀具的底圆角,在没有干涉的情况下,可选择更大的刀具直径,这样刀具的刚性也更好,如图 3所示。
|
图 2 球头铣刀和环形铣刀表面粗糙度理论值的比较 Figure 2 Comparison of theoretical values of surface racghness of ball-end milling tool and ring milling tool |
|
图 3 球头铣刀和环形铣刀刚性比较 Figure 3 Stiffness comparison of ball-end milling tool and ring milling tool |
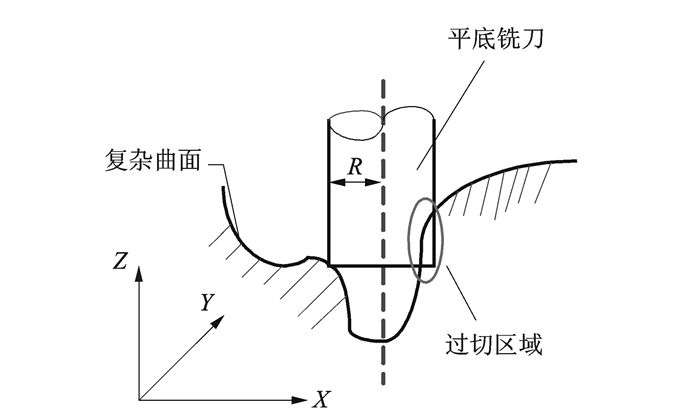
平头端铣刀的切削刃是刀具的端面与侧面的交界边缘线,其局限性一方面是加工时刀刃易于磨损,另一方面是由于平底端铣刀真正起切削作用的是刀刃口与刀具端面的交点,因此加工后留下的表面粗糙度较大,增加了后续磨削工序难度。同时,平底铣刀在加工复杂曲面时也容易出现过切的现象,如图 4所示。
|
图 4 平头端铣刀加工复杂曲面时的过切现象 Figure 4 Over-cutting phenomenon in milling complex curved surface by flat-end milling tool |
综上所述,环形铣刀同球头铣刀和平头端铣刀相比具有以下优点: (1) 切削性能好。环形铣刀没有尖锐的切削刃,与平底刀相比,被加工表面粗糙度要小很多,表面质量好。(2 ) 加工效率高。在获得同样的表面粗糙度的前提下,与球头铣刀相比,环形铣刀的步距要宽数倍,所以总切削长度变短,可大大地缩短加工时间。(3) 刀具寿命高,成本低。环形铣刀没有尖刃,刀具磨损相对较小。
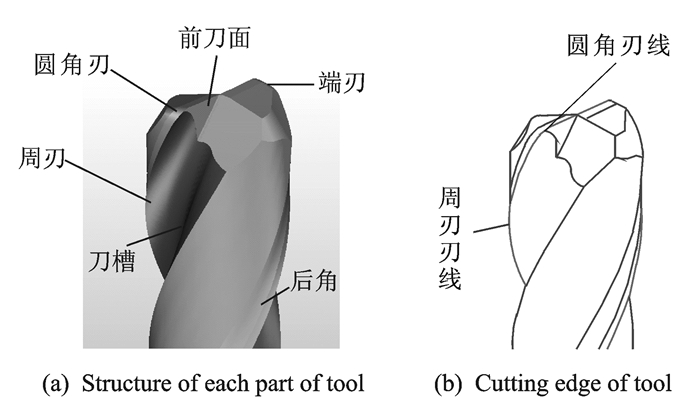
2 环形铣刀的几何结构解析环形铣刀是由3个部分组成,即圆柱侧面、底面和圆角面。环形铣刀刀具结构各部分名称如图 5所示。
|
图 5 环形铣刀 Figure 5 Ring milling tool |
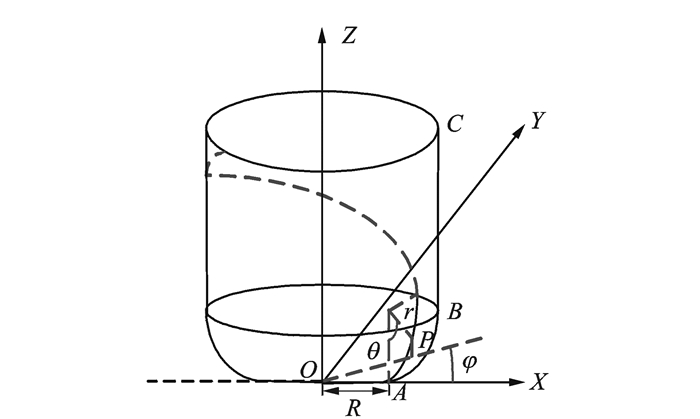
回转刀具的刃口曲线常常采用等螺旋角算法[9-10],以下讨论对等螺旋角环形铣刀刃口曲线建模,也包括周刃刃线与圆角刃线。图 6为环形铣刀坐标系。在坐标系中,以半径为r的角圆其圆心到Z轴距离为R。用刃线上任意点P依次旋转θ和φ角度来表达刃线的方程,其中θ和φ为刃口曲线方程的自变量。
|
图 6 环形铣刀坐标系 Figure 6 Coordinate system of ring milling tool |
当绕Z轴回转时所得回转面方程为
| $ \begin{array}{*{20}{c}} {{r_1} = \left\{ {\left( {R + r\sin \theta } \right)\cos {\varphi _1},\left( {R + r\sin \theta } \right)\sin {\varphi _1},} \right.}\\ {\left. {r\left( {1 - \cos \theta } \right)} \right\}\;\;\;\theta \in [0,\pi /2],\varphi \in [0,2\pi ]} \end{array} $ | (1) |
运用曲面第一基本形式得
| $ {r_1}\theta = \left\{ {r\cos \theta \sin {\varphi _1},r\cos \theta \cos {\varphi _1},r\sin \theta } \right\}\; $ | (2) |
| $ {r_1}\varphi = \left\{ { - \left( {R + r\sin \theta } \right)\sin {\varphi _1},\left( {R + r\sin \theta } \right)\cos {\varphi _1},0} \right\} $ | (3) |
则第一类基本量为
| $ E = {r_1}{\theta ^2} = {r^2} $ |
| $ F = {r_1}\theta * {r_1}\varphi = 0 $ |
| $ G = {r_1}{\varphi _1}^2 = {\left( {R + r\sin \theta } \right)^2} $ |
若螺旋角为β,则有
| $ {\cos ^2}\beta = \frac{{Ed{\theta ^2}}}{{Ed{\theta ^2} + Ed\bar w_1^{ - 2}}} $ | (4) |
| $ d{\varphi _1} = \frac{{r\tan \beta }}{{R + r\sin \theta }}d\theta $ | (5) |
式(5)两边同时积分得
| $ \begin{matrix} {{\varphi }_{1}}=-\frac{2r}{R\sin \vartriangle }\times \tan \beta \times \\ \left[ arctan\left( \tan \frac{\vartriangle }{2}\tan \frac{\pi /2-\theta }{2} \right) \right]+C \\ \end{matrix} $ | (6) |
将初始值φ1=0°,θ=0°代入式(6)求得
| $ C=\frac{2r}{R\sin \vartriangle }\times \tan \beta $ | (7) |
因此
| $ \begin{matrix} {{\varphi }_{1}}=-\frac{2r}{R\sin \vartriangle }\times \tan \beta \times \\ \left[ arctan\left( \tan \frac{\vartriangle }{2}\tan \frac{\pi /2-\theta }{2} \right)-\frac{\vartriangle }{2} \right] \\ \end{matrix} $ | (8) |
式中:Δ=arccos(r/R)。
将式(8)代入式(1)便可得到圆角回转面上刃口曲线,再考虑后接圆柱面刀刃曲线
| $ {{r}_{2}}=\left\{ \left( R+r \right)\cos {{\varphi }_{2}},\left( R+r \right)\sin {{\varphi }_{2}},r+{{Z}_{2}} \right\} $ | (9) |
式中:Z2∈[0,L],L为刀具的周刃长度;φ∈[0,2π]。依照式(2~4)可推出
| $ d{{\varphi }_{2}}=\frac{\tan \beta }{R+r}d{{Z}_{2}} $ | (10) |
为使螺旋刃口曲线连续,将$ \theta =\frac{\pi }{2} $代入式(8)得
| $ {{\varphi }_{1}}\text{=}\frac{r\vartriangle \tan \beta }{R\sin \vartriangle } $ | (11) |
对式(10)两边同时积分得
| $ {{\varphi }_{2}}\text{=}\frac{{{Z}_{2}}\tan \beta }{R+r}+\frac{r\vartriangle \tan \beta }{R\sin \vartriangle } $ | (12) |
将式(12)代入式(9)可得与圆角回转面上刃口连续的柱面上的螺旋刃口,且与其经线成定角。
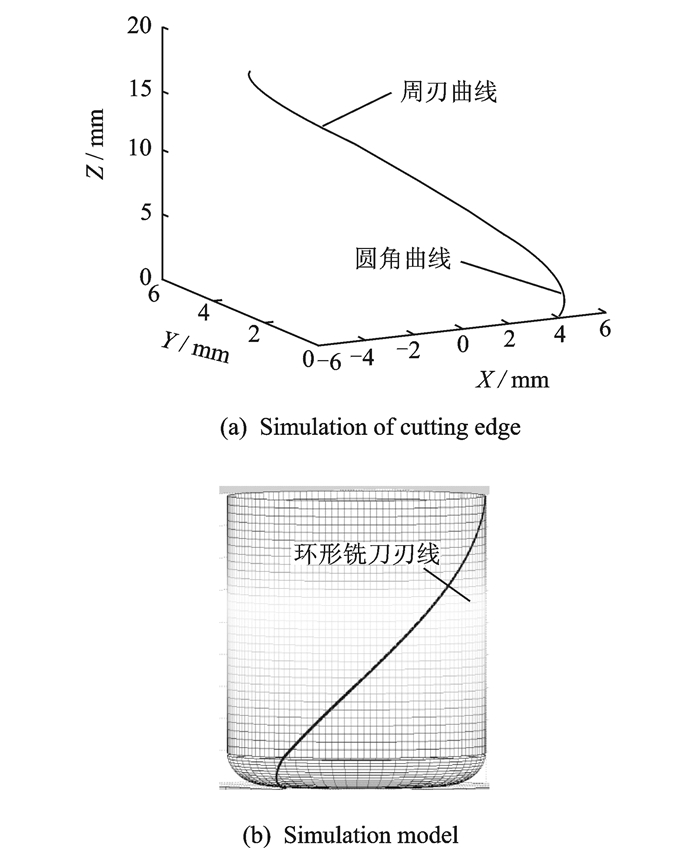
将式(8,12)分别代入式(1,9)可分别得出等螺旋角圆角刃口曲线方程和圆柱回转面上的刃口曲线方程。基于Matlab软件对得到的环形铣刀的刃口几何模型进行仿真,如图 7所示。
|
图 7 刃口几何模型仿真 Figure 7 Simulation of geometric model for cutting edge |
3 环形铣刀刃口曲线的连续性分析
环形铣刀圆柱面上的螺旋线和底部的圆角曲线的过渡,以及前刀面的过渡是刀具设计、制造的关键,本文对环形铣刀等螺旋角圆弧刃刃口曲线与圆柱面上的周刃刃口曲线在交汇处是矢量相同进行了论证。
由前面推导可知,将式(8,12)分别代入到式(1,9),可得到等螺旋角圆角刃口虚线方程和圆柱回转面上的刃口曲线方程。通过计算可得等螺旋角圆弧刃口曲线方程为
| $ {{r}_{1}}=\left\{ \begin{matrix} \left( R+r\sin \theta \right)\cos \left( -\frac{2r}{R\sin \vartriangle }\times \tan \beta \times \right. \\ \begin{matrix} \left. \left[ arctan\left( \tan \frac{\vartriangle }{2}\tan \frac{\pi /2-\theta }{2} \right)-\frac{\vartriangle }{2} \right] \right), \\ \begin{matrix} \left( R+r\sin \theta \right)\sin \left( -\frac{2r}{R\sin \vartriangle }\times \tan \beta \times \right. \\ \begin{matrix} \left. \left[ arctan\left( \tan \frac{\vartriangle }{2}\tan \frac{\pi /2-\theta }{2} \right)-\frac{\vartriangle }{2} \right] \right), \\ R\left( 1-\cos \theta \right) \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right\} $ | (13) |
环形铣刀的周刃刃口曲线方程为
| $ {{r}_{2}}=\left\{ \begin{matrix} \left( R+r \right)\cos \theta , \\ \left( R+r \right)\sin \left( \frac{{{z}_{2}}\tan \beta }{R+r}+\frac{r\vartriangle \tan \beta }{R\sin \vartriangle } \right), \\ R+{{Z}_{2}} \\ \end{matrix} \right\} $ | (14) |
在圆角面与圆柱面连接处,将$ \ \theta =\frac{\pi }{2} $,Z2=0代入式(13,14)有
| $ \begin{matrix} {{r}_{1}}=\left\{ \left( R+r \right)\cos \frac{r\vartriangle \tan \beta }{R\sin \vartriangle }, \right. \\ \left. \left( R+r \right)\sin \frac{r\vartriangle \tan \beta }{R\sin \vartriangle },r \right\} \\ \end{matrix} $ | (15) |
| $ {{r}_{2}}=\left\{ \left( R+r \right)\cos \frac{r\vartriangle \tan \beta }{R\sin \vartriangle },\left( R+r \right)\sin \frac{r\vartriangle \tan \beta }{R\sin \vartriangle },r \right\} $ | (16) |
由式(15,16)可知:r1=r2,即圆角回转面和柱面上等螺旋角刃口曲线在连接处连续,即环形铣刀在此处光滑过渡。圆柱面螺旋刃口和底部刃口曲线的光滑过渡保证了环形铣刀的磨制精度。
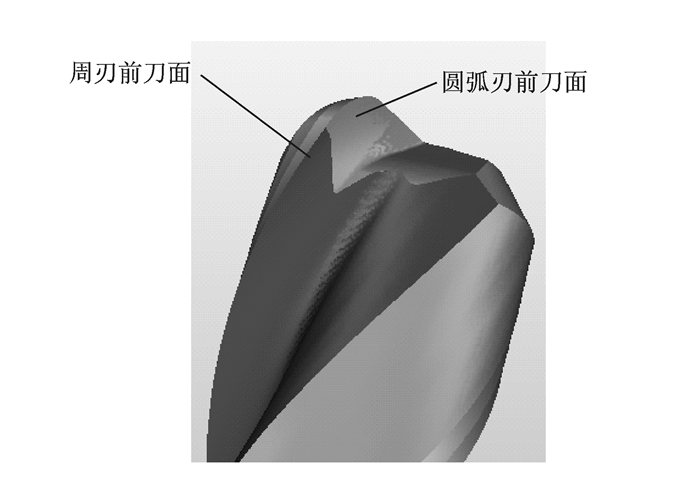
4 基于刃线方程的环形铣刀的磨制为了验证环形铣刀的磨制精度,基于所建立的环形铣刀的周刃、圆弧刃的几何模型以及刀具几何参数进行了环形铣刀的磨制,其中刀具的具体参数为r=2,R=4,L=16,β=30°,γ=2°,α1=8°,α2=22°。利用Saacke五轴工具磨床的Numroto磨削软件生产磨削轨迹,并对其进行仿真,保证环形铣刀周刃前刀面以及圆弧刃前刀面能够光滑过渡,其仿真结果如图 8所示。最终运用Saacke五轴工具磨床对其进行磨制,磨制过程如图 9 (a)所示,所得到的环形铣刀如图 9 (b)所示。
|
图 8 环形铣刀磨削轨迹的仿真 Figure 8 Simulation of grinding track for ring milling tool |

|
图 9 环形铣刀磨制过程及结果 Figure 9 Grinding process and result of ring milling tool |
5 结束语
在淬硬钢铣削工艺中,周边切削刃与底面切削刃以一小段圆弧过渡的环形铣刀与球头铣刀和平头端铣刀相比,在加工精度、表面质量和切削效率方面具有较高的综合优势。结合环形铣刀加工原理以及回转刀具螺旋线成形原理的理论分析,本文建立了典型环形铣刀的圆角刃与周刃的曲线模型,该模型较好地解决了环形铣刀的刃形建模问题。基于所建立的铣刀模型,本文利用Saacke五轴工具磨床进行了环形铣刀的磨制,检测结果表明刀具磨制精度较高。本文研究结果为环形铣刀的研制及切削性能的提高提供了理论基础。
| [1] |
王扬渝.多硬度拼接淬硬钢铣削动力学研究[D].杭州:浙江工业大学,2013. Wang Yangyu.Milling dynamics on assembled hardened steel with different hardness[D].Hangzhou:Zhejiang University of Technology, 2013. |
| [2] |
张安山, 刘献礼, 李茂月, 等. 汽车覆盖件模具的非球头刀宽行加工方法. 哈尔滨理工大学学报[J], 2014,19 (1)
:6–7.
Zhang Anshan, Liu Xianli, Li Maoyue, et al. An approach to non- ball-end milling of automobile cove ring mold with large machining strip width. Journal of Harbin University of Science and Technology[J], 2014, 19 (1) :6–7 . |
| [3] |
任秉银, 唐余勇.
数控加工中的几何建模理论及其应用[M]. 哈尔滨: 哈尔滨工业大学出版杜, 2000 : 76 -84.
Ren Bingyin, Tang Yuyong. The theory of geometric modeling and the application for CNC machining[M]. Harbin: Harbin Institute of Technology Press, 2000 : 76 -84. |
| [4] |
陈逢军.基于五轴数控磨床加工的球头立铣刀数学模型及仿真研究[D].长沙:湖南大学,2006. Chen Fengjun. The research on simulation and mathematical model of ball-end tools based on five-axis numerial control grinder[D].Changsha:Hunan University,2006. |
| [5] |
鲍青山, 汪云涛, 唐余勇. 回转铣刀刃口曲线通式、应用与连续. 黑龙江大学自然科学学报[J], 1999,16 (4)
:32–35.
Bao Qingshan, Wang Yuntao, Tang Yuyong. Current equation, application and continuity of bladecurve on rotative milling cutter. Journal of Natural Science of Heilongjiang University[J], 1999, 16 (4) :32–35 . |
| [6] |
唐余勇, 鲍青山, 汪云涛. 带角圆的凸弧回转铣刀上新型刃口设计. 黑龙江大学自然科学学报[J], 2003,20 (2)
:45–47.
Tang Yuyong, Bao Qingshan, Wang Yuntao. New design of the cutting edge on the arc revolving cutters with toroidal shape. Journal of Natural Science of Heilongjiang University[J], 2003, 20 (2) :45–47 . |
| [7] |
唐余勇, 姚强. 有关带角圆的凸弧铣刀的探讨. 黑龙江大学自然科学学报[J], 2000,17 (1)
:22–24.
Tang Yuyong, Yao Qiang. Research on the arc revolving cutters with toroidal shape. Journal of Natural Science of Heilongjiang University[J], 2000, 17 (1) :22–24 . |
| [8] |
韩琦. 模具加工用刀具的新概念. 机械工人[J], 2007 (7)
:29–30.
Han Qi. The new concept of cutter for mold processing. Machinery Workers[J], 2007 (7) :29–30 . |
| [9] |
龚智辉, 宾鸿赞. 螺旋角的广义定义及其应用. 中国机械工程[J], 1994,5 (1)
:14–15.
Gong Zhihui, Bin Hongzan. The generalized definition and application of the helix angle. Mechanical Engineering of China[J], 1994, 5 (1) :14–15 . |
| [10] |
张学奇, 唐余勇. 三沟槽等螺旋角带角圆铣刀设计的数学模型. 机械科学与技术[J], 2002,21 (6)
:886–887.
Zhang Xueqi, Tang Yuyong. A mathematic model for design of trigroove equiscrew-angle milling cutter with circle-angle. Mechanical Science and Technology[J], 2002, 21 (6) :886–887 . |
 2016, Vol. 48
2016, Vol. 48


