2. 中国科学院光电研究所, 北京, 100094
2. China Academy of Sciences Institute of Optoelectronics, Beijing, 100094, China
工业机器人在航空、航天及飞机数字化装配中的应用越来越多,其绝对定位精度显得尤为重要。机器人定位精度是指末端实际位姿与理论位姿之间误差的大小。对于现阶段的大多数工业机器人,影响其绝对定位精度的因素主要有运动学误差和动力学误差两类,而定位误差的80%来源于运动学误差,因此大多数运动学参数标定方法以辨识几何参数误差为主。国内外学者在运动学参数标定方面建树很多,参数标定一般经过误差模型建立、测量、参数辨识及误差补偿这4个步骤[1]。随着激光跟踪仪技术的发展,标定方法的区分主要在建模和参数辨识算法上有所不同。建模方面,Hayati[2]改进了D-H模型,解决了标定过程中的奇异问题;Stone[3]建立了S模型对机器人运动学参数进行了标定;Zhuang等[4]以CPC(Complete and parametrically continous)模型和MCPC模型为基础对机器人进行了标定;Chen等[5]在基于POE公式的基础上对机器人运动学参数进行了标定。而国内学者基本沿用国外提出的模型,并在辨识算法上做了一定的改进,杨丽红等[6]先用跟踪仪拟合出扭转角并在推导出末端位置误差模型的基础上用最小二乘法辨识了参数;龚星如等[7]在误差模型的基础上增加了激光跟踪仪坐标系与机器人坐标系转换的误差矩阵,并用最小二乘算法辨识了参数;李定坤[8]利用基于距离误差模型的总体最小二乘法辨识了运动学参数,避免了跟踪仪与机器人基坐标系转换的误差。
然而,由于末端位姿误差产生的原因不仅仅是连杆参数误差所带来的,还有动力学因素(关节柔性、连杆柔性以、摩擦力及重力影响等)。马培荪等[9]通过对机器人末端位姿误差进行了概率分析,得出末端误差在某些特定关节处偏差较大;因此继续沿用上述最小二乘辨识算法会引起运动学参数标定的不确定度,造成拟合参数时产生一定偏差[10]。对于误差分布比较合理时,参数辨识时利用最小二乘进行拟合即可得到最优估计,而当末端误差波动较大时,继续拟合往往造成一定偏差,本文引入基于抗差估计的运动学参数标定方法,通过抑制末端位姿误差较大的点来优化参数标定结果。因此本文算法将适合于更复杂、不太稳定的工业机器人标定环境,具有较强的鲁棒性。
1 机器人末端位姿误差模型本文以ABB IRB2600 20/1.65型机器人为例,如图 1所示,首先建立其连杆坐标系。

|
图 1 ABB IRB2600的结构图及其连杆坐标系 Figure 1 Structure of ABB IRB2600 and its joint link coordinate system |
在基于连杆坐标系的基础上,对相邻的连杆坐标系进行变换,转换矩阵Ai如下
| $ \begin{array}{*{20}{c}} {{}^{i - 1}{\mathit{\boldsymbol{T}}_i} = {\mathit{\boldsymbol{A}}_i} = {\rm{Rot}}\left( {z,{\theta _i}} \right) \times {\rm{Tran}}\left( {0,0,{d_i}} \right) \times }\\ {{\rm{Tran}}\left( {{a_i},0,0} \right) \times {\rm{Rot}}\left( {x,{\alpha _i}} \right) = }\\ {\left[ {\begin{array}{*{20}{c}} {\cos {\theta _i}}&{ - \sin {\theta _i}\cos {\alpha _i}}&{\sin {\theta _i}\sin {\alpha _i}}&{{a_i}\cos {\theta _i}}\\ {\sin {\theta _i}}&{\cos {\theta _i}\cos {\alpha _i}}&{ - \cos {\theta _i}\sin {\alpha _i}}&{{a_i}\sin {\theta _i}}\\ 0&{\sin {\alpha _i}}&{\cos {\alpha _i}}&{{d_i}}\\ 0&0&0&1 \end{array}} \right]} \end{array} $ | (1) |
式中:αi,ai,di,θi表示D-H参数。根据连杆坐标系以及D-H参数可得D-H参数的理论值,如表 1所示。则
| $ {\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}&0&{ - \sin {\theta _1}}&{{a_1}\cos {\theta _1}}\\ {\sin {\theta _1}}&0&{\cos {\theta _1}}&{{a_1}\sin {\theta _1}}\\ 0&{ - 1}&0&{{d_1}}\\ 0&0&0&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _2}}&{ - \sin {\theta _2}}&0&{{a_2}\cos {\theta _2}}\\ {\sin {\theta _2}}&{\cos {\theta _2}}&0&{{a_2}\sin {\theta _2}}\\ 0&0&1&{{d_2}}\\ 0&0&0&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_3} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _3}}&0&{ - \sin {\theta _3}}&{{a_3}\cos {\theta _3}}\\ {\sin {\theta _3}}&0&{\cos {\theta _3}}&{{a_3}\sin {\theta _3}}\\ 0&{ - 1}&0&{{d_3}}\\ 0&0&0&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_4} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _4}}&0&{\sin {\theta _4}}&{{a_4}\cos {\theta _4}}\\ {\sin {\theta _4}}&0&{ - \cos {\theta _4}}&{{a_4}\sin {\theta _4}}\\ 0&1&0&{{d_4}}\\ 0&0&0&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_5} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _5}}&0&{ - \sin {\theta _5}}&{{a_5}\cos {\theta _5}}\\ {\sin {\theta _5}}&0&{\cos {\theta _5}}&{{a_5}\sin {\theta _5}}\\ 0&{ - 1}&0&{{d_5}}\\ 0&0&0&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_6} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _6}}&{ - \sin {\theta _6}}&0&{{a_6}\cos {\theta _6}}\\ {\sin {\theta _6}}&{\cos {\theta _6}}&0&{{a_6}\sin {\theta _6}}\\ 0&0&1&{{d_6}}\\ 0&0&0&1 \end{array}} \right] $ | (2) |
| 表 1 D-H参数理论值 Table 1 Theoretical values of D-H parameters |
那么机器人末端的法兰坐标系相对于基坐标系的位姿变换矩阵如下
| $ \begin{array}{*{20}{c}} {{}_0^6\mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{A}}_2} \cdot {\mathit{\boldsymbol{A}}_3} \cdot {\mathit{\boldsymbol{A}}_4} \cdot {\mathit{\boldsymbol{A}}_5} \cdot {\mathit{\boldsymbol{A}}_6} = }\\ {\left[ {\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}&{{p_x}}\\ {{n_y}}&{{o_y}}&{{a_y}}&{{p_y}}\\ {{n_z}}&{{o_z}}&{{a_z}}&{{p_z}}\\ 0&0&0&1 \end{array}} \right]} \end{array} $ | (3) |
式(3)右边矩阵为4×4的齐次矩阵。此处用PN表示法兰坐标系在基坐标系下的位姿06T,并写成函数形式为
| $ {\mathit{\boldsymbol{P}}^N} = \mathit{\boldsymbol{F}}\left( {a,d,\alpha ,\theta } \right) $ | (4) |
然而实际中运动学参数存在误差,则末端实际位姿PR为
| $ {\mathit{\boldsymbol{P}}^R} = \mathit{\boldsymbol{F}}\left( {a + \delta a,d + \delta d,\alpha + \delta \alpha ,\theta + \delta \theta } \right) $ | (5) |
那么位姿误差E为
| $ \mathit{\boldsymbol{E}} = {\mathit{\boldsymbol{P}}^R} - {\mathit{\boldsymbol{P}}^N} $ | (6) |
利用全微分[11]的方法可求得
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{}^1{J_6} \cdot {G_1}}&{{}^2{J_6} \cdot {G_2}}& \cdots &{{J_6} \cdot {G_6}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\delta {x_1}}\\ {\delta {x_2}}\\ \vdots \\ {\delta {x_6}} \end{array}} \right] $ | (7) |
其中位姿误差E是六维矢量,以及各矩阵具体表示如下
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{\rm{d}}x}&{{\rm{d}}y}&{{\rm{d}}z}&{\delta x}&{\delta y}&{\delta z} \end{array}} \right] $ |
| $ \delta {x_i} = \left[ {\begin{array}{*{20}{c}} {{\alpha _i}}&{{a_i}}&{{\theta _i}}&{{d_i}} \end{array}} \right] $ |
| $ {}^i{\mathit{\boldsymbol{J}}_6} = {\mathit{\boldsymbol{A}}_i} \cdot {\mathit{\boldsymbol{A}}_{i + 1}} \cdot \cdots \cdot {\mathit{\boldsymbol{A}}_6} $ |
| $ {\mathit{\boldsymbol{G}}_i} = \left[ {\begin{array}{*{20}{c}} 0&1&{{a_i}\sin {\alpha _i}}&0\\ 0&0&{{a_i}\cos {\alpha _i}}&{ - \sin {\alpha _i}}\\ 0&0&{ - {a_i}\sin {\alpha _i}}&{\cos {\alpha _i}}\\ 1&0&{ - \cos {\alpha _i}}&0\\ 0&0&0&0\\ 0&0&{\cos {\alpha _i}}&0 \end{array}} \right] $ | (8) |
将式(7)简写,得到关于连杆参数误差与末端位姿差的方程
| $ \mathit{\boldsymbol{E}} = \mathit{\boldsymbol{H}} \cdot \delta {x_i} $ | (9) |
H为6×24的矩阵,由于测量得到的位姿差E与全微分得到的理论位姿差H·δxi(连杆参数引起的位姿差)并不完全相等,存在误差v,因此将式(9)写成误差方程的形式为
| $ v = \mathit{\boldsymbol{H}} \cdot \delta {x_i} - \mathit{\boldsymbol{E}} $ | (10) |
式(10)表示运动学参数误差δxi与误差v之间的线性关系。
2 基于抗差估计的运动学参数标定原理 2.1 参数辨识算法标定过程中,由于机器人末端位姿误差源不仅仅是几何参数误差,而且某些特定作业场地中还有其他因素(如测量扰动以及跟踪仪测量误差),造成某些特定状态下位姿误差波动相对较大。本文基于以上原因,利用基于抗差估计的最小二乘法辨识运动学参数,使误差波动较大时也能正确分辨出运动学参数,使参数辨识的结果具有一定鲁棒性。
从章节1可得到连杆参数误差与末端位姿差之间的误差方程,末端位姿误差v服从正态分布时,利用最小二乘法辨识参数是最优估计,然而实际状态中,由于异常误差存在,继续使用最小二乘法将会使标准偏差扭曲,因此在最小二乘的基础上引入抗差估计。
抗差最小二乘法的总体思想是,改变最小二乘法中的权矩阵P,通过迭代使观测量E中波动较大的Ei所对应的权pi不断减小,这就起到抑制粗差的作用。其过程为:首先根据理论D-H参数、关节角度值以及末端测量值建立误差方程,并对系数阵H进行QR分解,剔除不能辨识的运动学参数[12],重新组成误差方程。根据误差方程(10)求解未知参数δxi,第一次求解时,P为单位权,得
| $ \delta x_i^K = \left( {{\mathit{\boldsymbol{H}}^{\rm{T}}} \cdot {\mathit{\boldsymbol{P}}^K} \cdot \mathit{\boldsymbol{H}}} \right) \cdot {\mathit{\boldsymbol{H}}^{\rm{T}}} \cdot {\mathit{\boldsymbol{P}}^K} \cdot {\mathit{\boldsymbol{E}}^K} $ | (11) |
式中K为第K次迭代,以下各式均表示第K次迭代式的状态。初次求解时,K=0。将求解的未知参数δxiK代入式(10)计算末端位姿差的残差
| $ v_i^K = \mathit{\boldsymbol{H}} \cdot \delta x_i^K - {\mathit{\boldsymbol{E}}^K} $ | (12) |
由式(12)得到的残差进而重新定权
| $ \bar p_i^K = {p_i} \cdot \frac{{\psi \left( {v_i^K} \right)}}{{v_i^K}} $ | (13) |
式中:pi是权矩阵P对角线上i行i列元素,ψ(viK)为关于残差viK的权因子函数。将得到新的权矩阵代入式(11)继续求解未知参数,继续迭代,直到max|dx|<ε。
2.2 等价权的选取设计权因子函数有3个原则:限制利用有用信息;充分利用有效信息;排除有害信息。使得权因子随着残差绝对值增大而减小,直至为0。参数平差时常用的等价权函数主要以下4类[13]。
(1) Huber权函数
| $ {{\bar p}_i} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {p_i}\\ {p_i}c/\left| {{v_i}} \right| \end{array}&\begin{array}{l} \left| {{v_i}} \right| \le c\\ \left| {{v_i}} \right| > c \end{array} \end{array}} \right. $ | (14) |
(2) Tukey权函数
| $ {{\bar p}_i} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {p_i}{\left( {1 - {{\left( {{v_i}/c} \right)}^2}} \right)^2}\\ 0 \end{array}&\begin{array}{l} \left| {{v_i}} \right| \le c\\ \left| {{v_i}} \right| > c \end{array} \end{array}} \right. $ | (15) |
(3) IGG1权函数
| $ {{\bar p}_i} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {p_i}\\ {p_i}{k_0}/\left| {{v_i}} \right|\\ 0 \end{array}&\begin{array}{l} \left| {{v_i}} \right| \le {k_0}\\ {k_0} < \left| {{v_i}} \right| \le {k_1}\\ \left| {{v_i}} \right| > {k_1} \end{array} \end{array}} \right. $ | (16) |
(4) IGG3权函数
| $ \begin{array}{*{20}{c}} {{{\bar p}_i} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {p_i}\\ {p_i}\left( {{k_0}/\left| {{v_i}} \right|} \right)d_i^2\\ 0 \end{array}&\begin{array}{l} \left| {{v_i}} \right| \le {k_0}\\ {k_0} < \left| {{v_i}} \right| \le {k_1}\\ \left| {{v_i}} \right| > {k_1} \end{array} \end{array}} \right.}\\ {{d_i} = \frac{{{k_1} - \left| {{v_i}} \right|}}{{{k_1} - {k_0}}}} \end{array} $ | (17) |
对于4种权因子函数,前3种存在着不利于提高抗差性或者估计效率,而IGG3函数将末端误差分为3个阶段:正常段、可疑段以及排除段。对于机器人参数标定实验,采集到的点数一般在40个以上,其中大部分误差均处于正常段,基本服从正态分布,可疑段以及排除段占有很少一部分,因此在抗差最小二乘的过程中依然主要利用所有点的可靠信息,对于可疑段的点对其降权,异常点则予以排除,使其对应的权为0。因此本文算法所选取的权因子函数为IGG3权函数。式(17)中k0=1.5c,k1=2.5c,c为单位权中误差,由
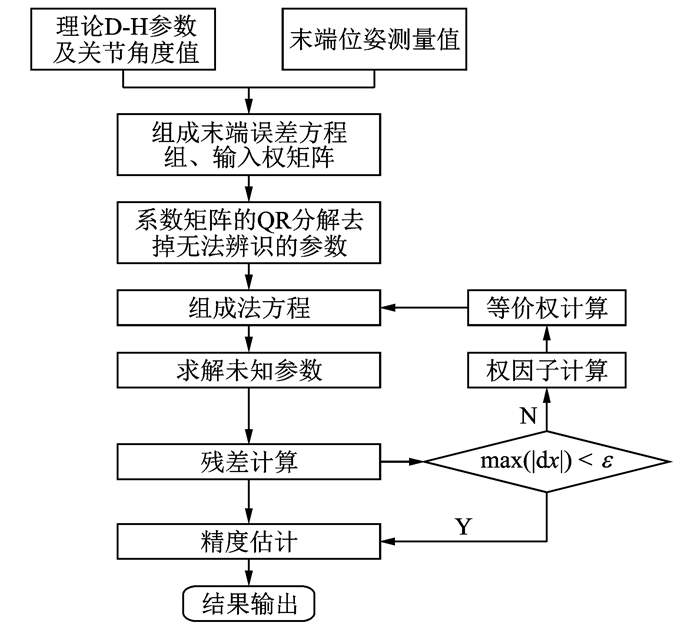
综合2.1及2.2所述,本文所提出的运动学参数标定方法整个过程如图 2所示。
|
图 2 标定算法流程图 Figure 2 Flowchart of calibration algorithm |
3 实验与分析
测量过程中使用的激光跟踪仪为Leica AT901-B型, 配合CCR1.5及CCR0.5角隅棱镜靶球, 以及用于测量末端位姿的probe,在2.5 m×5 m×10 m的工作范围内三维点坐标测量精度为±(15+6) μm,测角精度约为0.01°。
3.1 数据采集数据采集主要分为3个过程。
(1) 为了统一激光跟踪仪坐标系与机器人基坐标系,按照ABB技术文档中基坐标系的定义用激光跟踪仪拟合基坐标系[14],此后跟踪仪采集的数据均可通过SA测量软件转换到基坐标系下。
(2) 工具坐标系与法兰坐标系相对位姿关系的标定。在机器人某一固定位姿下,利用激光跟踪仪按照法兰坐标系定义拟合出法兰坐标系,安装probe后,SA所得到的(X Y Z RX RY RZ)为工具坐标系在跟踪仪下位姿数据,经过转换即可得到工具相对于跟踪仪的位姿矩阵Ttooltr,根据下式即可得到工具相对于法兰的位姿矩阵Ttoolf。
| $ \mathit{\boldsymbol{T}}_f^{{\rm{tr}}} \cdot \mathit{\boldsymbol{T}}_{{\rm{tool}}}^f = \mathit{\boldsymbol{T}}_{{\rm{tool}}}^{{\rm{tr}}} $ | (18) |
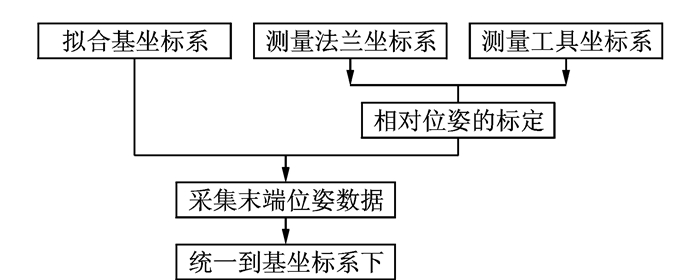
(3) 在机器人的工作空间内,控制机器人运动40个点,并在SA上记录40个位置的位姿测量值。实验数据采集过程如图 3所示。
|
图 3 实验流程图 Figure 3 Flowchart of the experiment |
3.2 标定结果
40个位姿测量值通过平移旋转关系可得到工具坐标系相对于激光跟踪仪坐标系齐次位姿矩阵,由3.1步骤1和2通过矩阵变换很容易得到法兰坐标系相对于基坐标系的位姿矩阵(测量值)PR。示教器所读出的理论法兰位姿数据格式为(X Y Z RZ RY RX),表示三维坐标和RPY形式的姿态。由示教器可读出的40组法兰位姿PN,最后根据第2节算法辨识出参数误差。表 2,3分别为两种算法辨识并补偿后的结果。
| 表 2 最小二乘法辨识的D-H参数 Table 2 D-H parameters by least square method |
| 表 3 抗差法辨识的D-H参数 Table 3 D-H parameters by robust estimation method |
为了比较两种算法辨识得到的参数的精确性,对于用户而言,机器人控制器内D-H参数无法改变,补偿可从六轴角度入手。为了验证补偿前后的精度,以40个点位作为目标位姿,分别用表 1—3的D-H参数逆解求40组六轴角度值,将每组角度值分别输入控制器中,示教器所读读数即为末端理论坐标,将机器人运动后对应的末端三维坐标与测量值作差,根据X轴、Y轴和Z轴方向误差计算定位误差
| $ e = \sqrt {\Delta {x^2} + \Delta {y^2} + \Delta {z^2}} $ | (19) |
式中:Δx,Δy,Δz分别为X轴,Y轴,Z轴方向误差。结果如表 4所示,分别列出了最大定位误差、平均定位误差以及平方根定位误差在补偿前后的变化。
| 表 4 补偿前后定位误差 Table 4 Positioning error before and after compensation |
3.3 精度分析
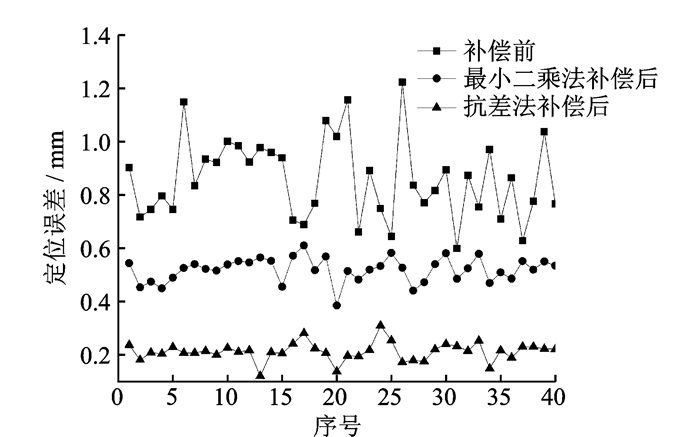
如图 4所示,两种方法补偿后定位精度均有一定提高。最大定位误差由补偿前的1.2 mm降低为补偿后的0.6 mm和0.3 mm,RMS误差从0.87 mm降低为0.52 mm和0.21 mm。对于辨识算法而言,抗差法优于最小二乘法,因为最小二乘法辨识参数时,将非几何参数误差所导致的末端位置误差波动较大的点位等权地拟合到D-H参数上,因此造成D-H参数相对真值有了一定偏移,而抗差法则抑制了这种现象,具有更优的补偿效果。
|
图 4 补偿前后的定位误差 Figure 4 Positioning error before and after compensation |
4 结束语
本文提出了一种基于抗差估计的工业机器人运动学参数标定的方法,该方法以IGG3等价权函数代替传统最小二乘法中的单位权,抑制了末端误差波动较大的点位,增强了算法的鲁棒性,提高了拟合精度。最后用基于D-H模型的ABB IRB2600型机器人进行了验证,结果表明,机器人绝对定位的RMS误差由补偿前的0.87 mm降低到0.21 mm,而且抗差法相对于最小二乘法效果更显著。本文方法经过改正也可辨识以MDH模型为基础的工业机器人的运动学参数。
但是,补偿后机器人定位仍然存在一定误差,这是因为此方法仅可较准确地辨识几何参数,对于非几何参数的辨识需在下一步工作中继续完善误差模型,辨识后即可进一步提高定位精度。
| [1] |
BAI Y, ZHUANG H, ROTH Z S. Experiment study of PUMA robot calibration using a laser tracking system[C]//Proceedings of IEEE International Workshop on Soft Computing in Industrial Applications. Piscataway, USA: IEEE, 2003: 139-144. |
| [2] |
HAYATI S A. Robot arm geometric link parameter estimation[C]//Proceedings of IEEE Decision and Control. San Antonio, USA: IEEE, 1983: 1477-1483. |
| [3] |
STONE H W. Kinematic modeling, identification, and control of robotic manipulators[D]. Pittsburgh, PA, USA: Carnegie Mellon University, 1987. |
| [4] |
ZHUANG H, ROTH Z S, HAMANO F.
A complete and parametrically continuous kinematic model for robot manipulators[J]. IEEE Transactions on Robotics & Automation, 2002, 8(4): 451–463.
|
| [5] |
CHEN I M, YANG G.
Kinematic calibration of modular reconfigurable robots using product of exponentials formula[J]. Journal of Robotic Systems, 1997, 14(11): 807–821.
DOI:10.1002/(ISSN)1097-4563
|
| [6] |
杨丽红, 秦绪祥, 蔡锦达, 等.
工业机器人定位精度标定技术的研究[J]. 控制工程, 2013, 20(4): 785–788.
DOI:10.3969/j.issn.1671-7848.2013.04.049 YANG Lihong, QIN Xuxiang, CAI Jinda, et al. Research on industrial robot's position accuracy calibration[J]. Control Engineering of China, 2013, 20(4): 785–788. DOI:10.3969/j.issn.1671-7848.2013.04.049 |
| [7] |
龚星如, 沈建新, 田威, 等.
工业机器人的绝对定位误差模型及其补偿算法[J]. 南京航空航天大学学报, 2012(S1): 60–64.
GONG Xingru, SHEN Jianxin, TIAN Wei, et al. Absolute position error of industrial robot and compensation algorithm[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012(S1): 60–64. |
| [8] |
李定坤.基于距离误差模型的机器人绝对精度标定研究[D].天津: 天津大学, 2007.
LI Dingkun. Study on robot's absolute accuracy calibration based on distance error model[D].Tianjin: Tianjin University, 2007. |
| [9] |
马培荪, 张新辉.
工业机器人运动误差的概率分析[J]. 上海交通大学学报, 1993, 27(1): 57–63.
MA Peisun, ZHANG Xinhui. Research of kinematic error analysis for industrial robot[J]. Journal of Shanghai Jiaotong University, 1993, 27(1): 57–63. |
| [10] |
李睿, 曲兴华.
工业机器人运动学参数标定误差不确定度研究[J]. 仪器仪表学报, 2014(10): 2192–2199.
LI Rui, QU Xinghua. Study on calibration uncertainty of industrial robot kinematic parameters[J]. Chinese Journal of Scientific Instrument, 2014(10): 2192–2199. |
| [11] |
夏天.工业机器人运动学标定及误差分析研究[D].上海: 上海交通大学, 2009.
XIA Tian. Research of kinematic calibration and error analysis for industrial robot[D].Shanghai: Shanghai Jiao Tong University, 2009. |
| [12] |
KHALIL W, DOMBRE E, NAGURKA M.
Modeling, identification and control of robots[M]. .
|
| [13] |
杨元喜.
等价权原理——参数平差模型的抗差最小二乘解[J]. 测绘通报, 1994(6): 33–35.
YANG Yuanxi. The principle of equivalent weight the robust least squares solution of uniformity model of the parameter adjustment[J]. Bulletin of Surveying and Mapping, 1994(6): 33–35. |
| [14] |
任永杰, 邾继贵, 杨学友, 等.
利用激光跟踪仪对机器人进行标定的方法[J]. 机械工程学报, 2007, 43(9): 195–200.
DOI:10.3321/j.issn:0577-6686.2007.09.038 REN Yongjie, ZHU Jigui, YANG Xueyou, et al. The method of robot calibration with laser tracker[J]. Journal of Mechanical Engineering, 2007, 43(9): 195–200. DOI:10.3321/j.issn:0577-6686.2007.09.038 |
 2018, Vol. 50
2018, Vol. 50


