高超声速飞行器是指飞行马赫数大于5的飞行器,它具有高超声速、高机动性、大航程等特点,对国防和民用都具有非常重要的意义。纵观高超声速飞行器的发展史,高超声速飞行试验过程并非是一帆风顺的,由试验失败而导致国家遭受巨大损失的案例非常多,因此先进的制导技术以及故障下容错技术是确保高超声速飞行器能够安全往返的首要前提[1]。
针对飞行器发生故障,飞行器轨迹重构制导技术方面,已经产生部分优秀的研究成果。文献[2-3]提出模型预测静态规划(Model predictive static programming, MPSP)算法,针对出现参数变化和干扰等异常情况下,实时调节控制量,实现再入鲁棒轨迹设计;呼卫军等人[4]采用动态伪谱法实现了运载器变更着陆点与控制能力下降情况下的应急再入轨迹重构。Ordóñez等人[5]基于相邻可行性轨迹存在定理(Neighboring feasible trajectory existence theorem, NFTET)和轨迹鲁棒定理(Trajectory robustness theorem, TRT)实现了飞行下降与着陆段的故障下轨迹重构。文献[6-7]将NFTET定理扩展至飞行再入返回阶段,采用预测校正算法生成标称轨迹, 处理微小故障与较大故障下的情况,完成了在线容错制导算法的设计。飞行器姿态容错控制方面也有许多优秀的研究成果,主要有滑模控制方法[8],Backstepping控制方法[9],自适应控制方法[10]和输出反馈控制方法[11]等方法。但故障时仅仅考虑对轨迹进行轨迹重构或者仅考虑对姿态进行容错控制,飞行器可能违背再入过程中的约束条件,同样无法使得飞行器达到飞行任务要求[1]。
目前,高超声速飞行器制导与控制系统通常采用传统的分离通道的制导与控制(Separate channel integrated guidance and control,SCIGC)设计方案:首先分别通过单独设计制导律和控制律,当两个子系统均满足预设的设计指标后,再将这两个子系统进行联合集成。目前已经有许多现代鲁棒控制方法分别应用于制导律和控制律的设计方案上。文献[12]采用预测校正制导算法生成了标称轨迹,直接将轨迹指令给到姿态环,采用Backstepping实现了飞行器的姿态控制。文献[13]中针对执行器故障或不确定参数等情况,集成内外环设计容错控制方法补偿故障影响,完成了集成自适应制导与控制方法的设计。Zong等人同时考虑制导环和姿态环,进行了整体性研究,采用伪谱法进行制导律设计、并设计双滑模控制器和干扰观测器对制导指令进行跟踪,完成了可重复使用运载器的集成再入制导与控制整体设计[14]。
由于制导环和控制环之间存在较强的耦合关系,若分开设计,这两个子系统之间的协同关系无法得到充分利用,整体系统的性能可能会受到限制,稳定性也无法得到保证。从而使得越来越多的学者对制导控制一体化(Integrated guidance and control,IGC)设计方案进行研究。制导控制一体化思想是根据当前飞行状态和任务目标直接生成飞行器所需的控制力矩指令并同时完成飞行制导和姿态控制任务。目前IGC设计思路可归纳为两类:(1)建立包含制导模型和姿态模型的6自由度全耦合模型,采用小增益控制[15]、反步控制[16]、动态面控制[17]和全状态反馈[18]等完成高阶非线性模型的控制器设计;(2)综合制导和姿态两个子系统的状态变量,提高制导与姿态环之间的集成度,对高阶非线性系统进行降阶处理,减小系统待设计控制变量,将IGC设计转换为低阶非线性系统的求解问题[19]。IGC设计可以提高飞行器的飞行性能,与传统的方法相比较,IGC设计可以减少控制器设计的迭代次数和所需传感器的数量与成本,并且IGC的设计考虑了各个子系统之间的耦合性,从而保证了系统的稳定性以及整体系统的可靠性。
针对以上问题,本文考虑控制系统存在的各种不确定性参数、外部干扰和力矩故障,通过选取中间制导变量建立包含再入制导模型和姿态模型的6自由度一体化模型。针对一体化模型,进行高超声速飞行器再入自适应容错制导控制一体化设计,并对设计的IGC控制策略进行稳定性分析。本文设计自适应滑模Backstepping容错控制器,并采用Takagi-Sugeno(T-S)模糊模型逼近由未知参数和加性故障引起的复合干扰项,基于Lyapunov稳定性定理设计参数自适应律,同时引入投影算子防止参数漂移以确保参数处于合理区间。通过IGC与SIGC控制策略仿真对比,验证了自适应容错IGC控制策略的有效性与优越性。
1 再入模型 1.1 再入制导模型在精度允许的条件下,假设高超声速飞行器的飞行侧滑角保持为零。本文采用不考虑地球自转, 质量恒定,大气稳定条件下的简化再入飞行运动方程[20]
| $ \dot V = - D/m - g\sin \gamma $ | (1) |
| $ \dot \gamma = \frac{{L\cos \sigma }}{{mV}} + \left( {\frac{V}{{{R_{\rm{e}}} + h}} - \frac{g}{V}} \right)\cos \gamma $ | (2) |
| $ \dot \psi = - \frac{{L\sin \sigma }}{{mV\cos \gamma }} + \frac{V}{{{R_{\rm{e}}} + h}}\cos \gamma \sin \psi \tan \varphi $ | (3) |
| $ \dot h = V\sin \gamma $ | (4) |
| $ \dot \theta = - \frac{{V\cos \gamma \sin \psi }}{{\left( {{R_{\rm{e}}} + h} \right)\cos \varphi }} $ | (5) |
| $ \dot \varphi = \frac{{V\cos \gamma \cos \psi }}{{{R_{\rm{e}}} + h}} $ | (6) |
式中:状态量x=[V, γ, ψ, h, θ, φ]T分别为速度、航迹角、航向角、高度、经度和纬度;控制量u=[α, σ]T分别为攻角和倾侧角;Re为地球平均半径;r=Re+h,为地心距;m为飞行器质量;g为重力加速度。L和D分别为升力和阻力,其表达式如下
| $ L = 0.5\rho {V^2}S{C_{\rm{L}}},D = 0.5\rho {V^2}S{C_{\rm{D}}} $ | (7) |
式中:S为飞行器的有效参考面积;ρ为大气密度;CL与CD分别表示升力系数和阻力系数。
升力系数CL和阻力系数CD采用拟合生成的关于攻角的函数,其形式如下
| $ {C_{\rm{L}}} = {C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha $ | (8) |
| $ {C_{\rm{D}}} = {C_{{{\rm{D}}_0}}} + {C_{{{\rm{D}}_1}}}\alpha $ | (9) |
再入姿态运动方程如下
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }} = \mathit{\boldsymbol{R}}\left( \cdot \right)\mathit{\boldsymbol{\omega }} $ | (10) |
| $ \mathit{\boldsymbol{\dot \omega }} = - {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} J\omega }} + {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{T}} $ | (11) |
式中:Θ=[α, σ, β]T为姿态角指令,分别是攻角、倾侧角和侧滑角;ω=[p, q, r]T为姿态角速度,p为滚转角速度,q为俯仰角速度,r为偏航角速度;R(·)∈R3×3,Ω∈R3×3和J∈R3×3的表达形式参见文献[21];T∈R3表示飞行控制力矩,通过设计合理的力矩,即可完成对飞行器再入飞行状态的控制。
1.3 故障模型飞行器故障主要有结构损伤、执行器故障、飞控效率的降低等,不同故障类型对飞行器有着不同的影响[22]。如文献[23]所述,由于复杂外界飞行环境引起的质心的偏移体现在控制力矩上的加性故障;舵面的长期动作出现的部分失效故障。故力矩故障模型可描述为
| $ \mathit{\boldsymbol{T}} = \mathit{\boldsymbol{\varepsilon }}\left( t \right){\mathit{\boldsymbol{T}}_e} + \mathit{\boldsymbol{f}}\left( {t,\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{\gamma }}} \right) $ | (12) |
式中,T为实际控制力矩;Te为期望的控制力矩;f(t, ω, γ)为力矩加性故障;ε(t)=diag(ε1, ε2, ε3),εi(i=1, 2, 3)为乘性故障失效因子,表征控制力矩的失效程度,有
对于分离通道的制导与控制策略,为了实现系统的整体性能要求,通常必须要调整各个子系统的设计参数,从而导致系统过度的迭代设计以及高额的成本,使得飞行器的整个设计过程变的更加复杂,可靠性也大大降低,稳定性也无法得到保障。因此,应考虑制导与控制的一体化设计,使飞行器在再入过程中始终处于瞬态平衡状态,并且能够保证姿态环实时跟踪上期望姿态指令,最大程度增强制导与控制系统在故障下的容错能力。
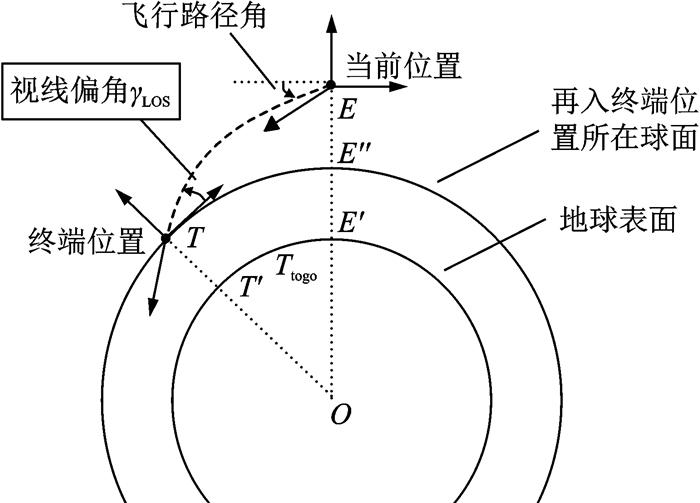
2 制导控制一体化模型为了消除纵向轨迹之间的偏差,本文定义了视线偏角γLOS,如图 1所示。
|
图 1 纵向角度之间的关系图 Figure 1 Relationship between the longitudinal angles |
由于地心距远远大于飞行高度,可将图形EE′T视为直角三角形,则可由如下式得γLOS
| $ \tan {\gamma _{{\rm{LOS}}}} = \frac{{{R_{\rm{e}}}\left( {h - h_f^ * } \right)}}{{\left( {{R_{\rm{e}}} + h_f^ * } \right){L_{{\rm{togo}}}}}} $ | (13) |
式中:Ltogo为剩余航程,Re为地球平均半径,hf*为飞行期望的终端高度。
由于视线偏角γLOS与飞行路径角γ的方向相反且γ≤0,则速度倾角误差Δγ为
| $ \Delta \gamma = {\gamma _{{\rm{LOS}}}} - \gamma $ | (14) |
侧向制导需要逐渐消除航向角误差Δψ
| $ \Delta \psi = {\psi _{{\rm{LOS}}}} - \psi $ | (15) |
式中, ψLOS为视线角。
则再入飞行制导任务为
| $ \mathop {\lim }\limits_{t \to {t_f}} \Delta \gamma = 0,\mathop {\lim }\limits_{t \to {t_f}} \Delta \psi = 0 $ | (16) |
分别根据高超声速飞行器再入制导任务,获得了速度倾角误差Δγ与航向角误差Δψ的微分表达式
| $ \begin{array}{*{20}{c}} {\Delta \dot \gamma = {{\dot \gamma }_{{\rm{LOS}}}} + \dot \gamma = }\\ {{{\dot \gamma }_{{\rm{LOS}}}} + \frac{{L\cos \sigma }}{{mV}} + \left( {\frac{V}{R} - \frac{g}{V}} \right)\cos \gamma = }\\ {{{\dot \gamma }_{{\rm{LOS}}}} + \left( {\frac{V}{R} - \frac{g}{V}} \right)\cos \gamma + \frac{{\rho VS}}{{2m}}{u_1}\left( {\alpha ,\sigma } \right)} \end{array} $ | (17) |
| $ \begin{array}{*{20}{c}} {\Delta \dot \psi = {{\dot \psi }_{LOS}} - \dot \psi = }\\ {{{\dot \psi }_{{\rm{LOS}}}} + \frac{{\rho VS{C_{\rm{L}}}\sin \sigma }}{{2m\cos \gamma }} - \frac{V}{R}\cos \gamma \sin \psi \tan \varphi = }\\ {{{\dot \psi }_{{\rm{LOS}}}} - \frac{V}{R}\cos \gamma \sin \psi \tan \varphi + \frac{{\rho VS}}{{2m\cos \gamma }}{u_2}\left( {\alpha ,\sigma } \right)} \end{array} $ | (18) |
式中
| $ {u_1}\left( {\alpha ,\sigma } \right){\rm{ = }}\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\cos \sigma $ |
| $ {u_2}\left( {\alpha ,\sigma } \right){\rm{ = }}\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\sin \sigma $ |
令x0=[Δγ Δψ]T,u=[u1 u2]T,则
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot x}}}_0} = \underbrace {\left[ {\begin{array}{*{20}{c}} {{{\dot \gamma }_{LOS}} + \left( {\frac{V}{R} - \frac{g}{V}} \right)\cos \gamma }\\ {{{\dot \psi }_{{\rm{LOS}}}} - \frac{V}{R}\cos \gamma \sin \psi \tan \varphi } \end{array}} \right]}_{\mathit{\boldsymbol{F}}\left( x \right)} + }\\ {\underbrace {\frac{{\rho S}}{{2m}}}_\vartheta \underbrace {\left[ {\begin{array}{*{20}{c}} V&0\\ 0&{\frac{V}{{\cos \gamma }}} \end{array}} \right]}_{\mathit{\boldsymbol{G}}\left( x \right)}\underbrace {\left[ {\begin{array}{*{20}{c}} {{u_1}\left( {\alpha ,\sigma } \right)}\\ {{u_2}\left( {\alpha ,\sigma } \right)} \end{array}} \right]}_{\mathit{\boldsymbol{u}}\left( {\alpha ,\sigma } \right)}} \end{array} $ | (19) |
由于本文研究的是高超声速飞行器再入段,-90° < γ < 90°,故G(x)是可逆的。
若已知制导中间变量u1(α, σ)、u2(α, σ),即可通过反插值分别解得所需的制导指令(攻角α、倾侧角σ)。将制导指令作用于制导模型,即可获得当前飞行器的飞行状态,从而完成飞行制导任务。
当飞行器发生故障时,飞行器质量和有效参考面积均有可能发生变化,同时大气密度本身就具有复杂多变的特点。故对于式(19)中,可将
| $ {{\mathit{\boldsymbol{\dot x}}}_0} = \mathit{\boldsymbol{F}}\left( x \right) + \vartheta \mathit{\boldsymbol{G}}\left( x \right)\mathit{\boldsymbol{u}}\left( {\alpha ,\sigma } \right) + {\mathit{\boldsymbol{d}}_0}\left( t \right) $ | (20) |
式中:
由于u(α, σ)为攻角与倾侧角的函数,而姿态控制是对姿态角进行实时跟踪,故姿态控制可直接跟踪制导中间变量u1(α, σ)、u2(α, σ),联立再入姿态运动方程式(10),可获得中间控制变量微分表达式
| $ \begin{array}{*{20}{c}} {{{\dot u}_1}\left( {\alpha ,\sigma } \right) = {C_{{L_1}}}\dot \alpha \cos \sigma - \left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\dot \sigma \sin \sigma = }\\ { - p\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\cos \alpha \sin \sigma + q{C_{{{\rm{L}}_1}}}\cos \sigma - }\\ {r\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\sin \alpha \sin \sigma } \end{array} $ | (21) |
| $ \begin{array}{*{20}{c}} {{{\dot u}_2}\left( {\alpha ,\sigma } \right) = {C_{{{\rm{L}}_1}}}\dot \alpha \sin \sigma + \left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\dot \sigma \cos \sigma = }\\ {p\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\cos \alpha \cos \sigma + q{C_{{{\rm{L}}_1}}}\sin \sigma + }\\ {r\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\sin \alpha \cos \sigma } \end{array} $ | (22) |
令x1=[u(α, σ) β]T,同时考虑由气动参数引起的控制系数矩阵偏差及外部干扰,则
| $ {{\mathit{\boldsymbol{\dot x}}}_1} = \left[ {\mathit{\boldsymbol{g}}\left( \cdot \right) + \mathit{\boldsymbol{g}}\left( \cdot \right)} \right]\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{d}}_1}\left( t \right) $ | (23) |
式中Δg(·)为控制系数矩阵不确定偏差,d1(t)为姿态角子系统的外部干扰项。
| $ \mathit{\boldsymbol{g}}\left( \cdot \right) = \left[ {\begin{array}{*{20}{c}} { - \left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\cos \alpha \sin \sigma }&{{C_{{{\rm{L}}_1}}}\cos \sigma }&{ - \left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\sin \alpha \sin \sigma }\\ {\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\cos \alpha \cos \sigma }&{{C_{{{\rm{L}}_1}}}\sin \sigma }&{\left( {{C_{{{\rm{L}}_0}}} + {C_{{{\rm{L}}_1}}}\alpha } \right)\sin \alpha \cos \sigma }\\ {\sin \alpha }&0&{ - \cos \alpha } \end{array}} \right] $ |
对于姿态角速率式(11),考虑不确定性参数和外部干扰,得
| $ \left( {\mathit{\boldsymbol{J}} + \Delta \mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{\dot \omega }} = - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\left( {\mathit{\boldsymbol{J}} + \Delta \mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{T}} + {\mathit{\boldsymbol{d}}_2}\left( t \right) $ | (24) |
式中:ΔJ为转动惯量矩阵J的不确定部分,d2(t)为姿态角速率子系统的外部干扰项。
当飞行器控制力矩发生如式(12)的故障时,可将包含有转动惯量矩阵的不确定部分ΔJ与控制力矩的加性故障融合到一起进行处理,令
| $ \mathit{\boldsymbol{\dot \omega }} = - {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} J\omega }} + {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{\varepsilon }}\left( t \right)\mathit{\boldsymbol{T}} + {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{D}} + {\mathit{\boldsymbol{J}}^{ - 1}}{\mathit{\boldsymbol{d}}_2}\left( t \right) $ | (25) |
联立式(20), (23)和(25),高超声速飞行器再入制导控制一体化模型为
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_0} = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + \vartheta \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{u}}\left( {\alpha ,\sigma } \right) + {\mathit{\boldsymbol{d}}_0}\left( t \right)\\ {{\mathit{\boldsymbol{\dot x}}}_1} = \left[ {\mathit{\boldsymbol{g}}\left( \cdot \right) + \mathit{\boldsymbol{g}}\left( \cdot \right)} \right]\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{d}}_1}\left( t \right)\\ \mathit{\boldsymbol{\dot \omega }} = - {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} J\omega }} + {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{\varepsilon }}\left( t \right)\mathit{\boldsymbol{T}} + {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{D}} + {\mathit{\boldsymbol{J}}^{ - 1}}{\mathit{\boldsymbol{d}}_2}\left( t \right) \end{array} \right. $ | (26) |
考虑高超声速飞行器发生控制力矩的加性故障和乘性故障,以及存在多种不确定性参数和外部干扰的情况,针对再入制导控制一体化模型式(26),设计自适应容错控制算法。
为方便系统控制器的设计,现将后续理论分析需要的引理、假设条件以及一些符号注解列举如下。
假设1 对于控制系数矩阵不确定偏差Δg(·),存在已知常数ξ≥0,使得||Δg(·)||≤ξ成立。
假设2 系统外部干扰项di(t)有界,存在正数ρi,满足||di(t)||≤ρi,i=0, 1, 2,其中,ρi为未知的干扰项上界。
假设3 控制力矩的加性故障f(t, ω, γ)为未知连续的非线性函数。
假设4 控制力矩的乘性故障失效因子εi(i=1, 2, 3)的下界
引理1[24] 对于任意常数ε0>0及任意η0∈R
| $ 0 \le \left| {{\eta _0}} \right| - {\eta _0}\tanh \left( {\frac{{{\eta _0}}}{{{\varepsilon _0}}}} \right) \le {k_{{\eta _0}}}{\varepsilon _0} $ |
式中:kη0为常数,且满足kη0=e-(kη0+1),即kη0=0.275 8。
注解1 ||·||为矩阵的Frobenius范数或向量的Euclidean范数,tr(·)为矩阵的迹;对于矩阵A和向量b,满足
注解2 定义tanh(si):=diag{tanh(
考虑制导控制一体化模型(26)的第一个方程式,为消除速度倾角误差Δγ与航向角误差Δψ。令e0=x0,选取如下滑模面
| $ {\mathit{\boldsymbol{s}}_0} = {\mathit{\boldsymbol{e}}_0} + {\mathit{\boldsymbol{K}}_0}\int_0^t {{\mathit{\boldsymbol{e}}_0}{\rm{d}}\tau } $ | (27) |
式中,s0=[s01 s02]T,增益矩阵K0=diag{k01 k02}且K0>0。
对式(27)求导,可得
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot s}}}_0} = {{\mathit{\boldsymbol{\dot e}}}_0} + {\mathit{\boldsymbol{K}}_0}{\mathit{\boldsymbol{e}}_0} = }\\ {\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + \vartheta \mathit{\boldsymbol{G}}\left( t \right)\mathit{\boldsymbol{u}}\left( {\alpha ,\sigma } \right) + {\mathit{\boldsymbol{d}}_0} + {\mathit{\boldsymbol{K}}_0}{\mathit{\boldsymbol{e}}_0}} \end{array} $ | (28) |
设计如下控制器
| $ {\mathit{\boldsymbol{u}}_d} = {\left( {\hat \vartheta \mathit{\boldsymbol{G}}} \right)^{ - 1}}\left( { - \mathit{\boldsymbol{F}} - \tanh \left( {{\mathit{\boldsymbol{s}}_0}} \right){{\mathit{\boldsymbol{\hat \rho }}}_0} - {\mathit{\boldsymbol{K}}_0}{\mathit{\boldsymbol{e}}_0}} \right) $ | (29) |
式中,
| $ \dot {\hat \vartheta} = {\mathit{\Lambda }_0}\left( {{\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_0} - {\zeta _0}\hat \vartheta } \right) $ | (30) |
| $ {{\mathit{\boldsymbol{\dot {\hat \rho} }}}_0} = {r_0}\left( {\tanh \left( {{\mathit{\boldsymbol{s}}_0}} \right){\mathit{\boldsymbol{s}}_0} - {\beta _0}{{\mathit{\boldsymbol{\hat \rho }}}_0}} \right) $ | (31) |
式中,Λ0>0,ζ0>0,r0>0,β0>0均为待设计参数,Tanh(·)详见本节注解2。
考虑一体化模型式(26)的第二个方程式,将姿态角速率ω作为虚拟控制变量,设计期望的角速率指令,实现对制导系统指令(x1=[u(α, σ) β]T)的跟踪。定义如下跟踪误差
| $ {\mathit{\boldsymbol{s}}_1} = {\mathit{\boldsymbol{x}}_1} - {\mathit{\boldsymbol{x}}_{1d}} $ | (32) |
式中,x1d为制导系统所生成的制导指令,由于制导期望侧滑角β为0,故x1d=[ud 0]T。
s1关于时间的导数为
| $ {{\mathit{\boldsymbol{\dot s}}}_1} = \left[ {\mathit{\boldsymbol{g}}\left( \cdot \right) + \Delta \mathit{\boldsymbol{g}}\left( \cdot \right)} \right]\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{d}}_1} - {{\mathit{\boldsymbol{\dot x}}}_{1d}} $ | (33) |
设计如下控制器
| $ {\mathit{\boldsymbol{\omega }}_d} = \left. {{\mathit{\boldsymbol{g}}^{ - 1}}\left( \cdot \right)\left( { - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{s}}_1} - \tanh \left( {{\mathit{\boldsymbol{s}}_1}} \right)} \right){{\mathit{\boldsymbol{\hat \rho }}}_1} + {{\mathit{\boldsymbol{\dot x}}}_{1d}}} \right) $ | (34) |
式中,K1=diag{k11 k12 k13}为反馈增益矩阵;
| $ {{\mathit{\boldsymbol{\dot {\hat \rho} }}}_1} = {r_1}\left( {\tanh \left( {{\mathit{\boldsymbol{s}}_1}} \right){\mathit{\boldsymbol{s}}_1} - {\beta _1}{{\mathit{\boldsymbol{\hat \rho }}}_1}} \right) $ | (35) |
式中,r1>0,β1>0为待设计参数。
考虑一体化模型的第三个方程式,设计期望的控制力矩,实现对姿态角速率ω的跟踪。定义姿态角速率跟踪误差
| $ {\mathit{\boldsymbol{s}}_2} = \mathit{\boldsymbol{\omega }} - {\mathit{\boldsymbol{\omega }}_d} $ | (36) |
式中,ωd为期望的角速率。
对式(36)求导,可得
| $ {{\mathit{\boldsymbol{\dot s}}}_2} = - {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} J\omega }} + {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{\varepsilon }}\left( t \right)\mathit{\boldsymbol{T}} + {\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{D}} + {\mathit{\boldsymbol{J}}^{ - 1}}{\mathit{\boldsymbol{d}}_2} - {{\mathit{\boldsymbol{\dot \omega }}}_d} $ | (37) |
设计如下自适应容错控制器
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{T}} = {{\mathit{\boldsymbol{\hat \varepsilon }}}^{ - 1}}\left( { - {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{s}}_2} - {\mathit{\boldsymbol{g}}^{\rm{T}}}\left( \cdot \right){\mathit{\boldsymbol{s}}_1} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} J\omega }} - } \right.}\\ {\left. {\tanh \left( {{\mathit{\boldsymbol{s}}_2}} \right){{\mathit{\boldsymbol{\hat \rho }}}_2} - \mathit{\boldsymbol{\hat D}} + \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_d} - \frac{{{\mathit{\boldsymbol{s}}_2}h\left( \mathit{\boldsymbol{s}} \right)}}{{{\chi ^2} + {{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|}^2}}}} \right)} \end{array} $ | (38) |
式中
| $ h\left( \mathit{\boldsymbol{s}} \right) = \mathit{\boldsymbol{s}}_0^{\rm{T}}{\mathit{\boldsymbol{K}}_0}{\mathit{\boldsymbol{s}}_0} + \xi \left\| {\mathit{\boldsymbol{s}}_1^{\rm{T}}} \right\|\left\| \mathit{\boldsymbol{\omega }} \right\| + \sum\limits_{i = 0}^2 {\frac{{{{\left\| {\mathit{\boldsymbol{\varphi }}_i^{\rm{T}}} \right\|}^2}}}{2}} $ |
| $ \dot \chi = \left\{ {\begin{array}{*{20}{c}} { - \frac{{\chi h\left( s \right)}}{{{\chi ^2} + {{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|}^2}}} - {k_v}\chi }&{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\| \ge \kappa }\\ 0&{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\| < \kappa } \end{array}} \right. $ |
式中:K2=diag{k21 k22 k23}为反馈增益矩阵;kv>0,κ>0;ξ为已知常数,使得||Δg(·)||≤ξ成立,详见假设1;φi=[kη0εi1 kη0εi2 … kη0εij]T,kη0>0。
| $ \dot {\hat \varepsilon} = {\mathit{\Lambda }_1}\left( {{\mathit{\boldsymbol{T}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_2} - {\zeta _1}\hat \varepsilon } \right) $ | (39) |
| $ {{\mathit{\boldsymbol{\dot {\hat \rho} }}}_2} = {r_2}\left( {\tanh \left( {{\mathit{\boldsymbol{s}}_2}} \right){\mathit{\boldsymbol{s}}_2} - {\beta _2}{{\mathit{\boldsymbol{\hat \rho }}}_2}} \right) $ | (40) |
式中,Λ1>0,ζ1>0,r2>0,β2>0。
由于T-S模糊逻辑系统可以任意精度一致逼近连续的非线性函数[25]。故考虑复合干扰项
由于ΔJ为转动惯量的不确定项,为常值,故定义如下模糊推理规则:
Ri:如果p是M1i,并且q是M2i,并且r是M3i,则
由平均加权反模糊化,得
| $ \mathit{\boldsymbol{D}} = \frac{{\sum\limits_{i = 1}^l {{\mathit{\boldsymbol{\mu }}_i}\left( \mathit{\boldsymbol{\omega }} \right)\left( {{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{\dot \omega }} + {\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{\omega }}} \right)} }}{{\sum\limits_{i = 1}^l {{\mu _i}\left( \mathit{\boldsymbol{\omega }} \right)} }} $ | (41) |
式中,μi(ω)由姿态角速率的模糊集合Mji(j=1, 2, 3)的隶属函数计算得到,且
| $ {\mu _i}\left( \mathit{\boldsymbol{\omega }} \right) = {R_i}\prod\limits_{j = 1}^3 {M_j^i} $ | (42) |
在实际计算中,常取认定权重Ri=1,以使计算方便简捷。
定义如下估计模型
| $ \mathit{\boldsymbol{\hat D}} = \frac{{\sum\limits_{i = 1}^l {{\mu _i}\left( \mathit{\boldsymbol{\omega }} \right)\left( {{{\mathit{\boldsymbol{\hat A}}}_i}\mathit{\boldsymbol{\dot \omega }} + {{\mathit{\boldsymbol{\hat B}}}_i}\mathit{\boldsymbol{\omega }}} \right)} }}{{\sum\limits_{i = 1}^l {{\mu _i}\left( \mathit{\boldsymbol{\omega }} \right)} }} $ | (43) |
式中:
D的估计误差
| $ \mathit{\boldsymbol{\tilde D}} = \mathit{\boldsymbol{\hat D}} - \mathit{\boldsymbol{D = }}\frac{{\sum\limits_{i = 1}^l {{\mu _i}\left( \mathit{\boldsymbol{\omega }} \right)\left( {{{\mathit{\boldsymbol{\tilde A}}}_i}\mathit{\boldsymbol{\dot \omega }} + {{\mathit{\boldsymbol{\tilde B}}}_i}\mathit{\boldsymbol{\omega }}} \right)} }}{{\sum\limits_{i = 1}^l {{\mu _i}\left( \mathit{\boldsymbol{\omega }} \right)} }} $ | (44) |
式中:
| $ {{\mathit{\boldsymbol{\dot {\hat A}}}}_i} = {\xi _{1i}}\left( {{w_i}{\mathit{\boldsymbol{s}}_2}{{\mathit{\boldsymbol{\dot \omega }}}^{\rm{T}}} - {\zeta _{1i}}{{\mathit{\boldsymbol{\hat A}}}_i}} \right) $ | (45) |
| $ {{\mathit{\boldsymbol{\dot {\hat B}}}}_i} = {\xi _{2i}}\left( {{w_i}{\mathit{\boldsymbol{s}}_2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}} - {\zeta _{2i}}{{\mathit{\boldsymbol{\hat B}}}_i}} \right) $ | (46) |
式中:
至此,根据再入任务,由自适应容错控制器式(38)得到期望的控制力矩,从而完成了高超声速飞行器再入自适应容错制导控制一体化设计。
3.2 投影算子为了保证自适应控制器中辨识参数的有界性,引入投影算子设计参数自适应律[26]。由于自适应律(30), (39)中,参数
| $ {\mathit{\Omega }_\vartheta } = \left\{ {\vartheta \left| {{\vartheta _{\min }} \le \vartheta \le {\vartheta _{\max }}} \right.} \right\} $ |
| $ {\mathit{\Omega }_\varepsilon } = \left\{ {\varepsilon \left| {{\varepsilon _{\min }} \le \varepsilon \le {\varepsilon _{\max }}} \right.} \right\} $ |
| $ {\mathit{\Omega }_{{\delta _\vartheta }}} = \left\{ {\vartheta \left| {{\vartheta _{\min }} - {\delta _\vartheta } \le \vartheta \le {\vartheta _{\max }} + {\delta _\vartheta }} \right.} \right\} $ |
| $ {\mathit{\Omega }_{{\delta _\varepsilon }}} = \left\{ {\varepsilon \left| {{\varepsilon _{\min }} - {\delta _\varepsilon } \le \varepsilon \le {\varepsilon _{\max }} + {\delta _\varepsilon }} \right.} \right\} $ |
式中:
定义投影算子Proj (
| $ {\rm{Proj}}\left( {\hat \vartheta ,{\lambda _0}} \right) = \left\{ \begin{array}{l} {\lambda _0}\;\;\;\;{\vartheta _{\min }} \le \hat \vartheta \le {\vartheta _{\max }},\\ \;\;\;\;\;\;\;或\;\hat \vartheta > {\vartheta _{\max }}\;且\;{\lambda _0} \le 0,\\ \;\;\;\;\;\;\;或\;\hat \vartheta < {\vartheta _{\min }}\;且\;{\lambda _0} \ge 0\\ {{\bar \lambda }_0}\;\;\;\hat \vartheta > {\vartheta _{\max }}\;且\;{\lambda _0} > 0\\ {{\bar \lambda }_0}\;\;\;\hat \vartheta < {\vartheta _{\min }}\;且\;{\lambda _0} < 0 \end{array} \right. $ | (47) |
式中
| $ {\lambda _0} = \dot {\hat \vartheta} = {\mathit{\Lambda }_0}\left( {{\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_0} - {\zeta _0}\hat \vartheta } \right) $ |
| $ {{\bar \lambda }_0} = \left( {1 + \frac{{{\vartheta _{\max }} - \hat \vartheta }}{{{\delta _\vartheta }}}} \right){\lambda _0} $ |
| $ {{\tilde \lambda } _0} = \left( {1 + \frac{{\hat \vartheta - {\vartheta _{\max }}}}{{{\delta _\vartheta }}}} \right){\lambda _0} $ |
定义投影算子Proj
| $ {\rm{Proj}}\left( {\hat \varepsilon ,{\lambda _1}} \right) = \left\{ \begin{array}{l} {\lambda _1}\;\;\;\;{\varepsilon _{\min }} \le \hat \varepsilon \le {\varepsilon _{\max }},\\ \;\;\;\;\;\;\;或\;\hat \varepsilon > {\varepsilon _{\max }}\;且\;{\lambda _1} \le 0,\\ \;\;\;\;\;\;\;或\;\hat \varepsilon < {\varepsilon _{\min }}\;且\;{\lambda _1} \ge 0\\ {{\bar \lambda }_1}\;\;\;\hat \varepsilon > {\varepsilon _{\max }}\;且\;{\lambda _1} > 0\\ {{\bar \lambda }_1}\;\;\;\hat \varepsilon < {\varepsilon _{\min }}\;且\;{\lambda _1} < 0 \end{array} \right. $ | (48) |
式中
| $ {\lambda _1} = \dot {\hat \varepsilon} = {{\mathit{\hat \Lambda }}_1}\left( {{\mathit{\boldsymbol{T}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_2} - {\zeta _1}\hat \varepsilon } \right) $ |
| $ {{\bar \lambda }_1} = \left( {1 + \frac{{{\varepsilon _{\max }} - \hat \varepsilon }}{{{\delta _\varepsilon }}}} \right){\lambda _1} $ |
| $ {{\tilde \lambda }_1} = \left( {1 + \frac{{\hat \varepsilon - {\varepsilon _{\min }}}}{{{\delta _\varepsilon }}}} \right){\lambda _1} $ |
引入投影算子,
| $ \dot \vartheta = {\rm{Proj}}\left( {\vartheta ,{\lambda _0}} \right) $ | (49) |
| $ \dot \varepsilon = {\rm{Proj}}\left( {\hat \varepsilon ,{\lambda _1}} \right) $ | (50) |
容易证明,当
针对高阶时变非线性制导控制一体化系统模型(26),3.1节中设计的再入自适应容错制导控制一体化控制策略可描述为以下定理。
定理1 针对高超声速飞行器再入制导控制一体化系统模型(26),在满足假设条件(1—4)的情况下,考虑系统存在多种不确定参数及外界干扰,当飞行器发生控制力矩故障时,本文所设计的自适应容错IGC控制策略(29), (34), (38)和参数自适应估计律(31), (35), (40), (45), (46), (49), (50)可以保证系统的有界稳定。
证明
对于IGC闭环控制系统,选择如下Lyapunov方程
| $ \begin{array}{*{20}{c}} {V = \frac{1}{2}\sum\limits_{i = 0}^1 {\mathit{\boldsymbol{s}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_i}} + \frac{1}{2}\mathit{\boldsymbol{s}}_2^{\rm{T}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{s}}_2} + \frac{1}{2}\sum\limits_{i = 0}^2 {\frac{1}{{{r_i}}}\mathit{\boldsymbol{\tilde \rho }}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde \rho }}}_i}} + }\\ {\frac{1}{2}{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}\tilde \vartheta + \frac{1}{2}{{\tilde \varepsilon }^{\rm{T}}}\mathit{\Lambda }_1^{ - 1}\tilde \varepsilon + }\\ {\sum\limits_{i = 1}^l {\left( {{\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde A}}}_i}}}{{2{\xi _{1i}}}}} \right) + {\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde B}}}_i}}}{{2{\xi _{2i}}}}} \right)} \right)} + \frac{1}{2}{\chi ^2}} \end{array} $ | (51) |
式中, 为表示形式的统一,
对Lyapunov方程求导,得
| $ \begin{array}{*{20}{c}} {\dot V = \sum\limits_{i = 0}^1 {\mathit{\boldsymbol{s}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_i} + \mathit{\boldsymbol{s}}_2^{\rm{T}}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot s}}}_2}} + \sum\limits_{i = 0}^2 {\frac{1}{{{r_i}}}\mathit{\boldsymbol{\tilde \rho }}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat \rho} }}}_i}} + {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}\dot {\hat \vartheta} + }\\ {{{\tilde \varepsilon }^{\rm{T}}}\mathit{\Lambda }_1^{ - 1}\dot {\hat \varepsilon} + \sum\limits_{i = 1}^l {\left( {{\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat A}}}}_i}}}{{{\xi _{1i}}}}} \right) + {\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat B}}}}_i}}}{{{\xi _{2i}}}}} \right)} \right) + \chi \dot \chi } } \end{array} $ | (52) |
由一体化控制策略控式(29), (34), (38),可获得
| $ {{\mathit{\boldsymbol{\dot s}}}_0} = - {\tilde \vartheta } \mathit{\boldsymbol{Gu}} - \tanh \left( {{\mathit{\boldsymbol{s}}_0}} \right){{\mathit{\boldsymbol{\hat \rho }}}_0} + {\mathit{\boldsymbol{d}}_0} $ | (53) |
| $ {{\mathit{\boldsymbol{\dot s}}}_1} = - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{s}}_1} - \tanh \left( {{\mathit{\boldsymbol{s}}_1}} \right){{\mathit{\boldsymbol{\hat \rho }}}_1} + \mathit{\boldsymbol{g}}\left( \cdot \right){\mathit{\boldsymbol{s}}_2} + \Delta \mathit{\boldsymbol{g}}\left( \cdot \right)\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{d}}_1} $ | (54) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot s}}}_2} = - {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{s}}_2} - \tilde \varepsilon T - {\mathit{\boldsymbol{g}}^{\rm{T}}}\left( \cdot \right){\mathit{\boldsymbol{s}}_1} - \mathit{\boldsymbol{\tilde D}} - }\\ {\tanh \left( {{\mathit{\boldsymbol{s}}_2}} \right){{\mathit{\boldsymbol{\hat \rho }}}_2} + {\mathit{\boldsymbol{d}}_2} - \frac{{{\mathit{\boldsymbol{s}}_2}h\left( \mathit{\boldsymbol{s}} \right)}}{{{\chi ^2} + {{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|}^2}}}} \end{array} $ | (55) |
式中:
结合引理1,考虑如下不等式关系
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{s}}_m^{\rm{T}}{\mathit{\boldsymbol{d}}_m} \le \sum\limits_{i = 1}^n {\left| {{s_{mi}}} \right|{\rho _{mi}}} \le }\\ {\sum\limits_{i = 1}^n {\left( {{k_{{\eta _0}}}{\varepsilon _{mi}} + {s_{mi}}\tanh \left( {\frac{{{s_{mi}}}}{{{\varepsilon _{mi}}}}} \right)} \right){\rho _{mi}}} = }\\ {\mathit{\boldsymbol{\varphi }}_m^{\rm{T}}{\mathit{\boldsymbol{\rho }}_m} + \mathit{\boldsymbol{s}}_m^{\rm{T}}\tanh \left( {{\mathit{\boldsymbol{s}}_m}} \right){\mathit{\boldsymbol{\rho }}_m} \le }\\ {\mathit{\boldsymbol{s}}_m^{\rm{T}}\tanh \left( {{\mathit{\boldsymbol{s}}_m}} \right){\mathit{\boldsymbol{\rho }}_m} + \frac{{{{\left\| {\mathit{\boldsymbol{\varphi }}_m^{\rm{T}}} \right\|}^2}}}{2} + \frac{{{{\left\| {{\mathit{\boldsymbol{\rho }}_m}} \right\|}^2}}}{2}} \end{array} $ | (56) |
式中,n为向量sm(m=0, 1, 2)的维数。则s0Tṡ0, s1Tṡ1, s2TJṡ2不等式关系如下所示
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{s}}_0^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_0} = \mathit{\boldsymbol{s}}_0^{\rm{T}}\left[ { - {\tilde \vartheta } \mathit{\boldsymbol{Gu}} - \tanh \left( {{\mathit{\boldsymbol{s}}_0}} \right){{\mathit{\boldsymbol{\hat \rho }}}_0} + {\mathit{\boldsymbol{d}}_0}} \right] \le }\\ { - \mathit{\boldsymbol{s}}_0^{\rm{T}}\tilde \vartheta \mathit{\boldsymbol{Gu}} - \mathit{\boldsymbol{s}}_0^{\rm{T}}\tanh \left( {{\mathit{\boldsymbol{s}}_0}} \right){{\mathit{\boldsymbol{\tilde \rho }}}_0} + \frac{{{{\left\| {\mathit{\boldsymbol{\varphi }}_0^{\rm{T}}} \right\|}^2}}}{2} + \frac{{{{\left\| {{\mathit{\boldsymbol{\rho }}_0}} \right\|}^2}}}{2}} \end{array} $ | (57) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{s}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_1} = \mathit{\boldsymbol{s}}_1^{\rm{T}}\left[ { - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{s}}_1} - \left. {\tanh \left( {{\mathit{\boldsymbol{s}}_1}} \right)} \right){{\mathit{\boldsymbol{\hat \rho }}}_1} + \mathit{\boldsymbol{g}}\left( \cdot \right){\mathit{\boldsymbol{s}}_2} + \Delta \mathit{\boldsymbol{g}}\left( \cdot \right)\mathit{\boldsymbol{\omega }} + } \right.}\\ {\left. {{\mathit{\boldsymbol{d}}_1}} \right] \le - \mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{s}}_1} - \mathit{\boldsymbol{s}}_1^{\rm{T}}\tanh \left. {\left( {{\mathit{\boldsymbol{s}}_1}} \right)} \right){{\mathit{\boldsymbol{\tilde \rho }}}_1} + \mathit{\boldsymbol{s}}_1^{\rm{T}}\mathit{\boldsymbol{g}}\left( \cdot \right){\mathit{\boldsymbol{s}}_2} + }\\ {\xi \left\| {\mathit{\boldsymbol{s}}_1^{\rm{T}}} \right\|\left\| \mathit{\boldsymbol{\omega }} \right\| + \frac{{{{\left\| {\mathit{\boldsymbol{\varphi }}_1^{\rm{T}}} \right\|}^2}}}{2} + \frac{{{{\left\| {{\mathit{\boldsymbol{\rho }}_1}} \right\|}^2}}}{2}} \end{array} $ | (58) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{s}}_2^{\rm{T}}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot s}}}_2} = \mathit{\boldsymbol{s}}_2^{\rm{T}}\left[ { - {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{s}}_2} - \mathit{\boldsymbol{\tilde \varepsilon T}} - {\mathit{\boldsymbol{g}}^{\rm{T}}}\left( \cdot \right){\mathit{\boldsymbol{s}}_1} - \mathit{\boldsymbol{\tilde D}} - } \right.}\\ {\left. {\tanh \left( {{\mathit{\boldsymbol{s}}_2}} \right){{\mathit{\boldsymbol{\hat \rho }}}_2} + {\mathit{\boldsymbol{d}}_2} - \frac{{{\mathit{\boldsymbol{s}}_2}h\left( \mathit{\boldsymbol{s}} \right)}}{{{\chi ^2} + {{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|}^2}}}} \right] \le }\\ { - \mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{s}}_2} - \tilde \varepsilon \mathit{\boldsymbol{s}}_2^{\rm{T}}\mathit{\boldsymbol{T}} - \mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{g}}^{\rm{T}}}\left( \cdot \right){\mathit{\boldsymbol{s}}_1} - \mathit{\boldsymbol{s}}_2^{\rm{T}}\mathit{\boldsymbol{\tilde D}} - }\\ {\mathit{\boldsymbol{s}}_2^{\rm{T}}\tanh \left( {{\mathit{\boldsymbol{s}}_2}} \right){{\mathit{\boldsymbol{\tilde \rho }}}_2} + \frac{{{{\left\| {\mathit{\boldsymbol{\varphi }}_2^{\rm{T}}} \right\|}^2}}}{2} + \frac{{{{\left\| {{\mathit{\boldsymbol{\rho }}_2}} \right\|}^2}}}{2} - }\\ {\frac{{\mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{s}}_2}h\left( \mathit{\boldsymbol{s}} \right)}}{{{\chi ^2} + {{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|}^2}}}} \end{array} $ | (59) |
式中,
基于自适应律式(31), (35), (47),外部干扰di(i=1, 2, 3)对应估计误差微分项
| $ \begin{array}{*{20}{c}} {\frac{1}{{{r_i}}}\mathit{\boldsymbol{\tilde \rho }}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat \rho} }}}_i} = \mathit{\boldsymbol{\tilde \rho }}_i^{\rm{T}}\left[ {\tanh \left( {{\mathit{\boldsymbol{s}}_i}} \right){\mathit{\boldsymbol{s}}_i} - {\beta _i}{{\mathit{\boldsymbol{\hat \rho }}}_i}} \right] \le }\\ {\mathit{\boldsymbol{\tilde \rho }}_i^{\rm{T}}\tanh \left( {{\mathit{\boldsymbol{s}}_i}} \right){\mathit{\boldsymbol{s}}_i} - \frac{{{\beta _i}}}{2}{{\left\| {{{\mathit{\boldsymbol{\tilde \rho }}}_i}} \right\|}^2} + \frac{{{\beta _i}}}{2}{{\left\| {{\mathit{\boldsymbol{\rho }}_i}} \right\|}^2}} \end{array} $ | (60) |
对于
(1) 当
| $ {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}\dot {\hat \vartheta} = {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0} $ |
(2) 当
| $ \begin{array}{*{20}{c}} {{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}\dot {\hat \vartheta} = {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{{\bar \lambda }_0} = {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0} + }\\ {\frac{{{\vartheta _{\max }} - \hat \vartheta }}{{{\delta _\vartheta }}}{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0} < {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0}} \end{array} $ |
(3) 当
| $ \begin{array}{*{20}{c}} {{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}\dot {\hat \vartheta} = {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{{\tilde \lambda }_0} = }\\ {{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0} + \frac{{\hat \vartheta - {\vartheta _{\min }}}}{{{\delta _\vartheta }}}{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0} < }\\ {{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0}} \end{array} $ |
综上所述
| $ \begin{array}{*{20}{c}} {{{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}\dot {\hat \vartheta} \le {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}{\lambda _0} = }\\ {{{\tilde \vartheta }^{\rm{T}}}{\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_0} - {\zeta _0}{{\tilde \vartheta }^{\rm{T}}}\hat \vartheta \le }\\ {{{\tilde \vartheta }^{\rm{T}}}{\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_0} - \frac{{{\zeta _0}}}{2}{{\left\| {\tilde \vartheta } \right\|}^2} + \frac{{{\zeta _0}}}{2}{{\left\| \vartheta \right\|}^2}} \end{array} $ | (61) |
对于
| $ \begin{array}{*{20}{c}} {{{\tilde \varepsilon }^{\rm{T}}}\mathit{\Lambda }_1^{ - 1}\dot {\hat \varepsilon} \le {{\tilde \varepsilon }^{\rm{T}}}\mathit{\Lambda }_1^{ - 1}{\lambda _1} = }\\ {{{\tilde \varepsilon }^{\rm{T}}}{\mathit{\boldsymbol{T}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_2} - {\zeta _1}{{\tilde \varepsilon }^{\rm{T}}}\hat \varepsilon \le }\\ {{{\tilde \varepsilon }^{\rm{T}}}{\mathit{\boldsymbol{T}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_2} - \frac{{{\zeta _1}}}{2}{{\left\| {\tilde \varepsilon } \right\|}^2} + \frac{{{\zeta _1}}}{2}{{\left\| \varepsilon \right\|}^2}} \end{array} $ | (62) |
对于T-S模糊逻辑的估计项
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^l {\left( {{\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat A}}}}_i}}}{{{\xi _{1i}}}}} \right) + {\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat B}}}}_i}}}{{{\xi _{2i}}}}} \right)} \right)} = }\\ {{\rm{tr}}\left( {\sum\limits_{i = 1}^l {\left( {\frac{{\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat A}}}}_i}}}{{{\xi _{1i}}}} + \frac{{\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat B}}}}_i}}}{{{\xi _{2i}}}}} \right)} } \right) = }\\ {{\rm{tr}}\left[ {\sum\limits_{i = 1}^l {\left[ {\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}\left( {{w_i}{\mathit{\boldsymbol{s}}_2}{{\mathit{\boldsymbol{\dot \omega }}}^{\rm{T}}} - {\zeta _{1i}}{{\mathit{\boldsymbol{\tilde A}}}_i}} \right) + \mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}\left( {{w_i}{\mathit{\boldsymbol{s}}_2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}} - } \right.} \right.} } \right.}\\ {\left. {\left. {\left. {{\zeta _{2i}}{{\mathit{\boldsymbol{\hat B}}}_i}} \right)} \right]} \right) \le {\rm{tr}}\left( {\sum\limits_{i = 1}^l {{w_i}\left( {\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_2}{{\mathit{\boldsymbol{\dot \omega }}}^{\rm{T}}} + \mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}} \right)} } \right) + }\\ {\frac{{{\zeta _{1i}}}}{2}\left( {{{\left\| {{\mathit{\boldsymbol{A}}_i}} \right\|}^2} - {{\left\| {\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}} \right\|}^2}} \right) + \frac{{{\zeta _{2i}}}}{2}\left( {{{\left\| {{\mathit{\boldsymbol{B}}_i}} \right\|}^2} - {{\left\| {\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}} \right\|}^2}} \right)} \end{array} $ | (63) |
由式(38)中,χ的动态方程得
| $ \frac{{{\chi ^2}h\left( \mathit{\boldsymbol{s}} \right)}}{{{\chi ^2} + {{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|}^2}}} + \chi \dot \chi = - {k_v}{\chi ^2} $ | (64) |
故Lyapunov方程的一阶导为
| $ \begin{array}{*{20}{c}} {\dot V = \sum\limits_{i = 0}^1 {\mathit{\boldsymbol{s}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_i}} + \mathit{\boldsymbol{s}}_2^{\rm{T}}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot s}}}_2} + \sum\limits_{i = 0}^2 {\frac{1}{{{r_i}}}} \mathit{\boldsymbol{\tilde \rho }}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat \rho} }}}_i} + {{\tilde \vartheta }^{\rm{T}}}\mathit{\Lambda }_0^{ - 1}\dot {\hat \vartheta} + }\\ {{{\tilde \varepsilon }^{\rm{T}}}\mathit{\Lambda }_1^{ - 1}\dot {\hat \varepsilon} + \sum\limits_{i = 1}^l {\left( {{\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat A}}}}_i}}}{{{\xi _{1i}}}}} \right) + {\rm{tr}}\left( {\frac{{\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat B}}}}_i}}}{{{\xi _{2i}}}}} \right)} \right)} + \chi \dot \chi \le }\\ { - \sum\limits_{j = 1}^2 {\mathit{\boldsymbol{s}}_j^{\rm{T}}{\mathit{\boldsymbol{K}}_j}{\mathit{\boldsymbol{s}}_j}} + \xi \left\| {\mathit{\boldsymbol{s}}_1^{\rm{T}}} \right\|\left\| \mathit{\boldsymbol{\omega }} \right\| - \mathit{\boldsymbol{s}}_2^{\rm{T}}\mathit{\boldsymbol{\tilde D}} - \frac{{\mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{s}}_2}h\left( \mathit{\boldsymbol{s}} \right)}}{{{\chi ^2} + {{\left\| {{\mathit{\boldsymbol{s}}_2}} \right\|}^2}}} + }\\ {\sum\limits_{i = 0}^2 {\left( {\frac{{{{\left\| {\mathit{\boldsymbol{\varphi }}_i^{\rm{T}}} \right\|}^2}}}{2} + \frac{{{{\left\| {{\mathit{\boldsymbol{\rho }}_i}} \right\|}^2}}}{2}} \right)} + \sum\limits_{i = 0}^2 {\left( {\frac{{{\beta _i}}}{2}{{\left\| {{\mathit{\boldsymbol{\rho }}_i}} \right\|}^2} + \frac{{{\beta _i}}}{2}{{\left\| {{{\mathit{\boldsymbol{\tilde \rho }}}_i}} \right\|}^2}} \right)} - }\\ {\frac{{{\zeta _0}}}{2}{{\left\| {\tilde \vartheta } \right\|}^2} + \frac{{{\zeta _0}}}{2}{{\left\| \vartheta \right\|}^2} - \frac{{{\zeta _1}}}{2}{{\left\| {\tilde \varepsilon } \right\|}^2} + \frac{{{\zeta _1}}}{2}{{\left\| \varepsilon \right\|}^2} + }\\ {{\rm{tr}}\left( {\sum\limits_{i = 1}^l {{w_i}\left( {\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_2}{{\mathit{\boldsymbol{\dot \omega }}}^{\rm{T}}} + \mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}{\mathit{\boldsymbol{s}}_2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}} \right)} } \right) + \chi \dot \chi + }\\ {\frac{{{\zeta _{1i}}}}{2}\left( {{{\left\| {{\mathit{\boldsymbol{A}}_i}} \right\|}^2} - {{\left\| {\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}} \right\|}^2}} \right) + \frac{{{\zeta _{2i}}}}{2}\left( {{{\left\| {{\mathit{\boldsymbol{B}}_i}} \right\|}^2} - {{\left\| {\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}} \right\|}^2}} \right) = }\\ { - \sum\limits_{j = 0}^2 {\mathit{\boldsymbol{s}}_j^{\rm{T}}{\mathit{\boldsymbol{K}}_j}{\mathit{\boldsymbol{s}}_j}} - \sum\limits_{i = 0}^2 {\frac{{{\beta _i}}}{2}{{\left\| {{{\mathit{\boldsymbol{\tilde \rho }}}_i}} \right\|}^2}} - \frac{{{\zeta _0}}}{2}{{\left\| \vartheta \right\|}^2} - }\\ {\frac{{{\zeta _1}}}{2}{{\left\| {\tilde \varepsilon } \right\|}^2} - \frac{{{\zeta _{1i}}}}{2}{{\left\| {\mathit{\boldsymbol{\tilde A}}_i^{\rm{T}}} \right\|}^2} - \frac{{{\zeta _{2i}}}}{2}{{\left\| {\mathit{\boldsymbol{\tilde B}}_i^{\rm{T}}} \right\|}^2} - {k_v}{\chi ^2} + C \le }\\ { - \tau V + C} \end{array} $ | (65) |
式中
| $ \tau = \min \left\{ {{k_{ij}},\frac{{{\beta _i}}}{2},\frac{{{\zeta _0}}}{2},\frac{{{\zeta _1}}}{2},\frac{{{\zeta _{1i}}}}{2},\frac{{{\zeta _{2i}}}}{2},{k_v}} \right\} $ |
| $ \begin{array}{*{20}{c}} {C = \sum\limits_{i = 0}^2 {\frac{{\left( {1 + {\beta _i}} \right){{\left\| {{\mathit{\boldsymbol{\rho }}_i}} \right\|}^2}}}{2}} + \frac{{{\zeta _0}}}{2}{{\left\| \vartheta \right\|}^2} + }\\ {\frac{{{\zeta _1}}}{2}{{\left\| \varepsilon \right\|}^2} + \frac{{{\zeta _{1i}}}}{2}{{\left\| {\mathit{\boldsymbol{A}}_i^{\rm{T}}} \right\|}^2} - \frac{{{\zeta _{2i}}}}{2}{{\left\| {\mathit{\boldsymbol{B}}_i^{\rm{T}}} \right\|}^2}} \end{array} $ |
由于所设计参数均大于0,则τ>0始终成立。若V=l且τ>
| $ 0 \le V\left( t \right) \le \frac{C}{\tau } + \left( {V\left( 0 \right) - \frac{C}{\tau }} \right){{\rm{e}}^{ - \tau t}} $ | (66) |
由于不等式(64)表明V(t)是有界的,其边界为
根据以上的分析和推导,得出不确定参数、外部干扰以及故障因子的估计误差和动态表面都是一致最终有界。因此建立的闭环高阶非线性IGC控制系统是有界稳定。
4 仿真验证本文针对X-33总体与气动模型[21, 28],进行飞行器再入制导控制一体化方案性能测试。以下给定飞行器再入初始状态为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}^0} = {{\left[ {V,\gamma ,\psi ,h,\theta ,\varphi } \right]}^{\rm{T}}} = }\\ {{{\left[ {6\;500\;{\rm{m/s}},0,0,70\;{\rm{km,0,0}}} \right]}^{\rm{T}}}} \end{array} $ |
期望的终端位置:高度为25±2 km,速度为1 000±200 m/s,经/纬度为(15°±1°, 35°±1°)。攻角约束为[5°, 35°],倾侧角约束为[-70°, 70°]。转动惯量矩阵J
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {55\;486}&0&{ - 23\;002}\\ 0&{1\;136\;949}&0\\ { - 23\;002}&0&{1\;376\;852} \end{array}} \right]\;{\left( {{\rm{kg}} \cdot {\rm{m}}} \right)^2} $ |
高超声速飞行器再入初始姿态角Θ=[0, 0, 0]T(rad),初始姿态角速率ω=[0, 0, 0]T(rad·s-1),转动惯量的不确定部分ΔJ∈[-0.01J, +0.01J],制导环的外部干扰项d0(t)=[0.1, 0.2sin(0.5t)]T(rad·s-1),姿态角子系统的外部干扰项d1(t)=[0.5cos(t), 1, 0.25sin(t)]T(rad·s-1),姿态角速率子系统的外部干扰项d2(t)=[100cos(0.1t), 80sin(t), 200] (TN·m)。
本节根据高超声速飞行器发生故障情况,对飞行器没有发生故障和发生了力矩故障两种情况进行仿真验证。
仿真1 高超声速飞行器没有发生故障。
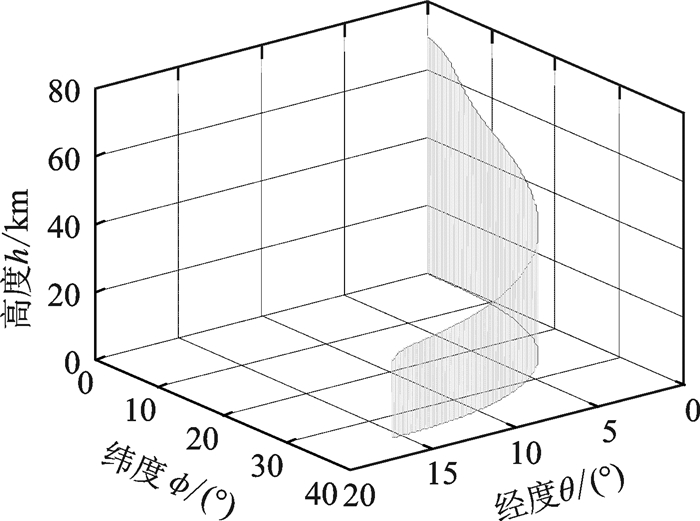
无故障时的仿真结果如图 2—3所示。图 2为采用制导控制一体化控制策略飞行器的再入飞行三维轨迹曲线,图 3为再入飞行过程中的状态变量和控制变量等响应曲线,由图 2—3可以看出,飞行器没有发生故障时,再入飞行过程中所有的状态变量及控制变量均满足所有的约束条件,能够生成可行的飞行轨迹,完成再入飞行任务。
|
图 2 三维再入轨迹(仿真1) Figure 2 Three-dimensional reentry trajectory (Simulation 1) |

|
图 3 制导状态量与控制量曲线(仿真1) Figure 3 The curves of guidance of state and control variables (Simulation 1) |
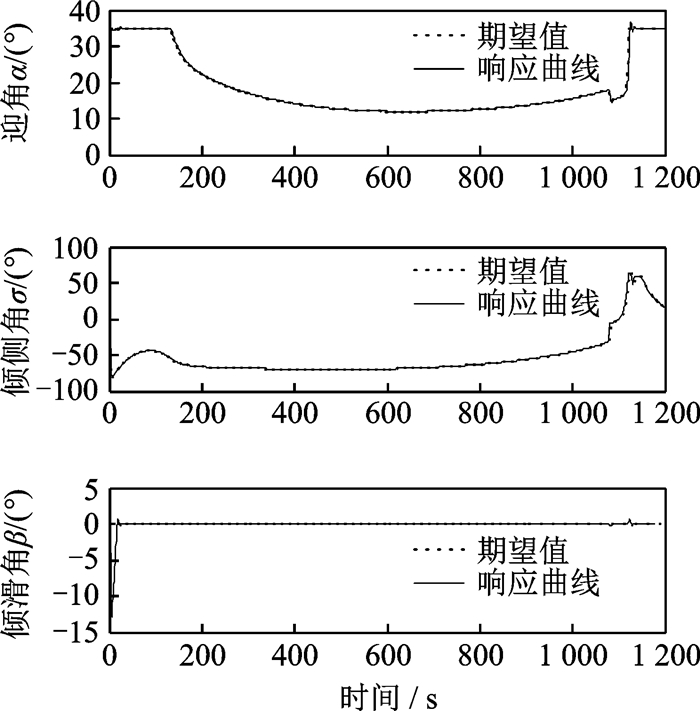
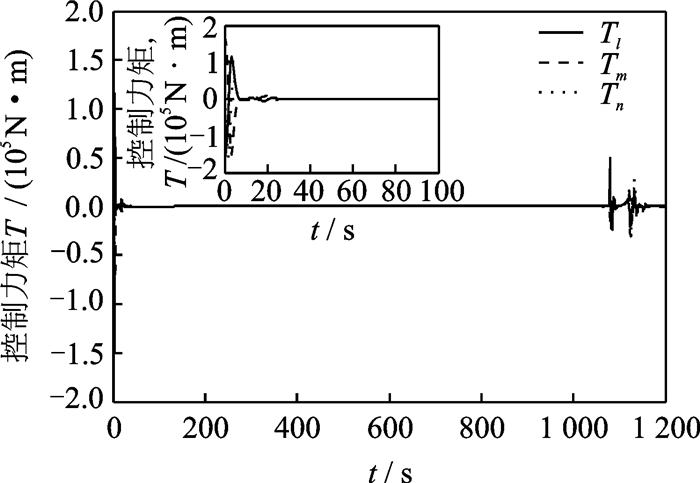
图 4和图 5给出了采用一体化控制策略时姿态角和姿态角速率的响应曲线。如图 4所示,姿态角响应曲线几乎完全实时跟踪上期望的参考指令。图 5中,姿态角速率在30 s左右就能够跟踪上期望的参考指令。飞行器控制力矩的响应曲线如图 6所示,力矩同样在30 s左右趋于有界。当飞行器姿态角速率跟踪上期望的角速率时,此时飞行器将保持稳定的姿态。
|
图 4 姿态角响应曲线(仿真1) Figure 4 Response curves of the attitude angle (Simulation 1) |

|
图 5 姿态角速率响应曲线(仿真1) Figure 5 Response curves of the attitude angular rate (Simulation 1) |
|
图 6 控制力矩响应曲线(仿真1) Figure 6 Response curves of the control torque (Simulation 1) |
本文所设计的高超声速飞行器再入自适应容错制导控制一体化策略能够生成可行的飞行轨迹,且姿态角及其角速率均能够实时跟踪上期望值,从而证明了该自适应一体化控制策略的有效性。
仿真2 高超声速飞行器控制力矩发生失效故障和加性故障。
为了更好地研究本文所设计的自适应容错制导控制一体化控制策略,将文献[29]中分离通道制导与控制环的控制策略与本文设计的制导控制一体化控制策略作比较。
假设当t≥40 s时,飞行器控制力矩发生加性故障,当t≥55 s时,飞行器控制力矩不仅发生加性故障,同时又发生了乘性故障,故障信息为
| $ \left\{ \begin{array}{l} 失效矩阵:\mathit{\boldsymbol{\varepsilon }}\left(t \right) = {\rm{diag}}\left({0.4, 0.8 + 0.1\sin \left(t \right), 0.7} \right)\\ 加性故障:\mathit{\boldsymbol{f}}\left({t, \mathit{\boldsymbol{\omega }}, \mathit{\boldsymbol{\gamma }}} \right) = {\mathit{\boldsymbol{f}}_1} + {\mathit{\boldsymbol{f}}_2} + {\mathit{\boldsymbol{f}}_3} \end{array} \right. $ |
式中
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_1} = \left[ {9 \times {{10}^3}\sin \left( {t/4} \right) + 1 \times {{10}^4}\left( {{p^2} + \exp \left( q \right)} \right),} \right.}\\ {2.5 \times {{10}^4},1 \times {{10}^4} + 2.5 \times {{10}^4}\cos \left( {t - 20} \right) - }\\ {{{\left. {2.5 \times {{10}^3}\exp \left( {\sigma + {\beta ^2}} \right)} \right]}^{\rm{T}}}} \end{array} $ |
| $ {\mathit{\boldsymbol{f}}_2} = {\rm{diag}}\left( { - 5 \times {{10}^3},7.5 \times {{10}^3},7.5 \times {{10}^3}} \right)\mathit{\boldsymbol{\gamma }} $ |
| $ {\mathit{\boldsymbol{f}}_3} = {\rm{diag}}\left( {7.5 \times {{10}^3},2.5 \times {{10}^3}, - 5 \times {{10}^3}} \right)\mathit{\boldsymbol{\omega }} $ |
故障下的仿真结果如图 7—12所示,IGC为本文设计控制策略,SCIGC为文献[29]中采用的分离通道制导与控制环的控制策略。

|
图 7 复合干扰项的实际值与估计值(仿真2) Figure 7 Actual value and estimated value of the complex interference term (Simulation 2) |
|
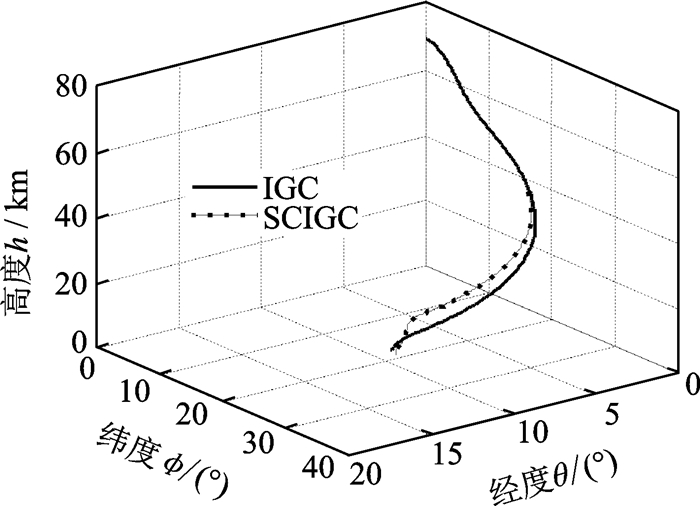
图 8 三维再入轨迹(仿真2) Figure 8 Three-dimensional reentry trajectory (Simulation 2) |
|
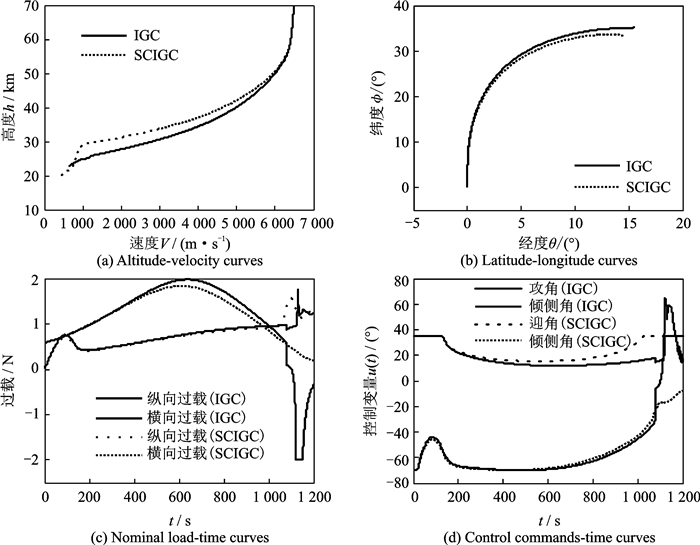
图 9 制导状态量与控制量曲线(仿真2) Figure 9 Curves of guidance of state and control variables (Simulation 2) |
|
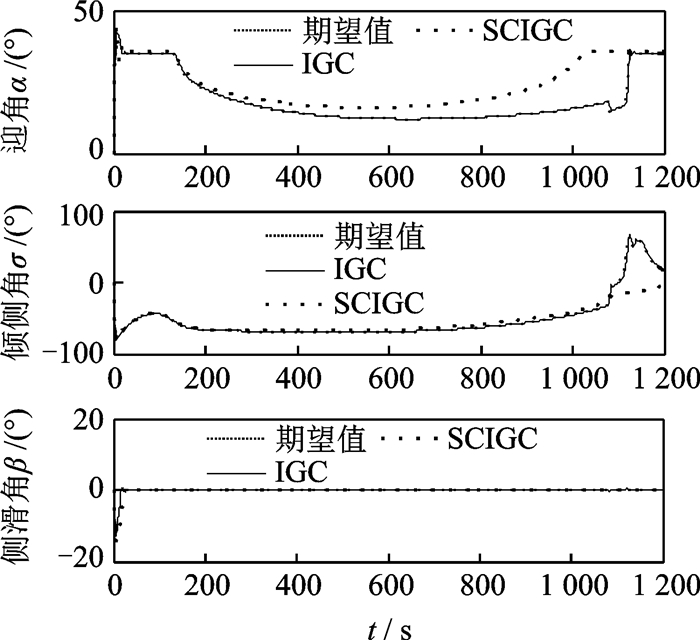
图 10 姿态角响应曲线(仿真2) Figure 10 Response curves of the attitude angle (Simulation 2) |
|
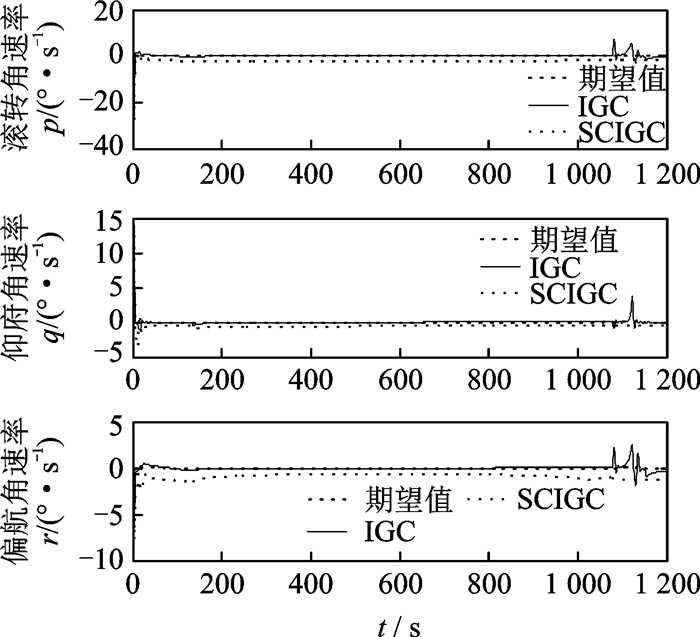
图 11 姿态角速率响应曲线(仿真2) Figure 11 Response curves of the attitude angular rate (Simulation 2) |
|
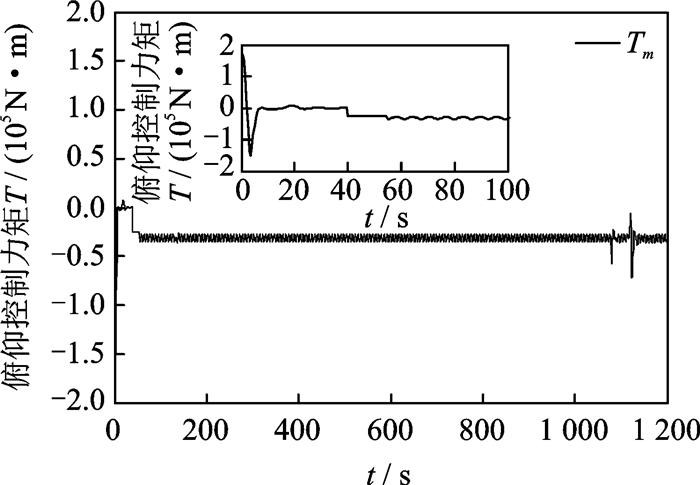
图 12 故障下俯仰控制力矩响应曲线(仿真2) Figure 12 Response curves of the pitch control torque under the fault (Simulation 2) |
由图 7所示,采用T-S模糊逻辑估计复合干扰项
图 8为飞行器发生故障后制导环生成的再入三维轨迹,图 9为飞行器制导过程的状态变量与控制变量。如图 8—9所示,采用本文IGC比SCIGC控制策略生成的轨迹终端位置与期望终端之间误差小,精度高。
姿态角的跟踪响应曲线如图 10所示,IGC控制策略能够实时跟踪上期望的姿态角,而SCIGC策略不能实时跟踪上期望值。图 11为姿态角速率的响应曲线,IGC策略能够跟踪上期望的角速率,并具有较高的跟踪精度,而SCIGC策略不能够跟踪上期望值,具有一定的跟踪误差,精度有限,本文设计的IGC控制策略较传统SCIGC控制策略具有较高的跟踪精度,控制效果具有一定的优越性,且生成满足可行的飞行轨迹,完成高超声速飞行器再入制导任务。
图 12—14给出了采用IGC控制策略的三通道控制力矩响应曲线,当飞行器在40 s后发生加性故障后,控制力矩发生了变化,通过T-S模糊逻辑估计力矩上的复合干扰项,然后由控制力矩提供同等大小的力矩来补偿故障及干扰对控制性能的影响。当55 s乘性故障发生后,其控制力矩变大,这是由于乘性故障发生后,控制力矩部分失效,作用于飞行器的力矩相应的被削弱,为保证控制性能的要求,故需要增加控制力矩的大小。在1 100~1 200 s时间段由于姿态角发生了较明显变化,三通道控制力矩也产生相应的控制力矩变化对飞行姿态角进行调节。

|
图 13 故障下滚转控制力矩响应曲线(仿真2) Figure 13 The response curves of the roll control torque under the fault (Simulation 2) |

|
图 14 故障下偏航控制力矩响应曲线(仿真2) Figure 14 Response curves of the yaw control torque under the fault (Simulation 2) |
5 结论
本文考虑控制系统存在各种不确定性参数和力矩故障,将高超声速飞行器再入段飞行制导环与姿态环融合,针对制导与控制一体化模型进行再入自适应容错制导控制一体化设计。
(1) 高超声速飞行器制导环与控制环之间存在强耦合特性。本文将制导模型的6个状态方程简化为关于制导指令的两个方程,联合姿态运动模型,考虑各种不确定性参数、外部干扰与力矩故障,获得制导控制一体化模型。
(2) 针对制导控制一体化模型,进行高超声速飞行器再入自适应容错制导控制一体化设计。设计自适应滑模Backstepping容错控制器,采用T-S模糊模型逼近由未知参数和加性故障引起的复合干扰项,基于Lyapunov稳定性定理设计参数自适应律,同时引入投影算子防止参数漂移,确保其处于合理区间。通过理论证明本文所设计的IGC控制策略能够有效保证高超声速飞行器姿态角及其角速率的实时跟踪,证明了该闭环高阶非线性IGC控制系统是有界稳定。
(3) 通过仿真验证,本文设计的T-S模糊逻辑逼近器能够高精度地估计由未知参数和加性故障引起的复合干扰项。由仿真结果可知,当飞行器发生故障后,采用SCIGC控制策略不能够完全跟踪上期望指令,而采用IGC控制策略能够实现跟踪,跟踪精度较高,且生成的再入轨迹满足任务要求,从而验证了本文设计的高超声速飞行器再入自适应容错制导控制一体化控制策略的有效性和优越性。
| [1] |
DUKEMAN G. Profile-following entry guidance using linear quadratic regulator theory[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.[S.l.]: AIAA, 2002. |
| [2] |
HALBE O, RAJA R G, PADHI R.
Robust reentry guidance of a reusable launch vehicle using model predictive static programming[J]. Journal of Guidance Control & Dynamics, 2013, 37(1): 134–148.
|
| [3] |
CHAWLA C, SARMAH P, PADHI R.
Suboptimal reentry guidance of a reusable launch vehicle using pitch plane maneuver[J]. Aerospace Science & Technology, 2010, 14(6): 377–386.
|
| [4] |
呼卫军, 周军, 常晶, 等.
RLV应急再入轨迹规划问题的动态伪谱法求解[J]. 宇航学报, 2015, 36(11): 1255–1261.
DOI:10.3873/j.issn.1000-1328.2015.11.006 HU Weijun, ZHOU Jun, CHANG Jing, et al. Emergency reentry trajectory planning for reusable launch vehicle based on dynamic gauss pseudo-spectral[J]. Journal of Astronautics, 2015, 36(11): 1255–1261. DOI:10.3873/j.issn.1000-1328.2015.11.006 |
| [5] |
JIANG Z, ORDÍÑEZ R.
On-line robust trajectory genera-tion on approach and landing for reusable launch vehicles[J]. Automatica, 2009, 45(7): 1668–1678.
DOI:10.1016/j.automatica.2009.03.017
|
| [6] |
钱佳淞, 齐瑞云.
基于NFTET的高超声速飞行器再入容错制导[J]. 航空学报, 2015, 36(10): 3370–3381.
QIAN Jiasong, QI Ruiyun. The study of the fault-tolerant guidance for reentry hypersonic flight vehicles based on NFTET[J]. Acta Aeronautica et As-tronautica Sinica, 2015, 36(10): 3370–3381. |
| [7] |
郭小平, 齐瑞云.
基于NFTET的高超声速飞行器鲁棒轨迹重构设计[J]. 南京航空航天大学学报, 2017, 49(S): 82–88.
GUO Xiaoping, QI Ruiyun. Design of robust trajectory reshaping for hypersonic vehicle based on NFTET[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2017, 49(S): 82–88. |
| [8] |
BASIN M, CALDERON-ALVAREZ D.
Sliding mode regulator as solution to optimal control problem for non-linear polynomial systems[J]. Journal of the Franklin Institute, 2010, 347(6): 910–922.
DOI:10.1016/j.jfranklin.2009.11.001
|
| [9] |
QI R Y, HUANG Y H, JIANG B, et al.
Adaptive backstepping control for hypersonic vehicle with uncertain parameters and actuator faults[J]. Proceedings of the Institution of Mechanical Engineers Part Ⅰ Journal of Systems & Control Engineering, 2013, 227(1): 51–61.
|
| [10] |
JIANG B, GAO Z, SHI P, et al.
Adaptive fault-tolerant tracking control of near-space vehicle using takagi-sugeno fuzzy models[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(5): 1000–1007.
DOI:10.1109/TFUZZ.2010.2058808
|
| [11] |
HE J, QI R, JIANG B, et al.
Adaptive output feedback fault-tolerant control design for hypersonic flight vehicles[J]. Journal of the Franklin Institute, 2015, 352(5): 1811–1835.
DOI:10.1016/j.jfranklin.2015.01.016
|
| [12] |
QIAN J, QI R, JIANG B. Fault-tolerant guidance and control design for reentry hypersonic flight vehicles based on control-allocation approach[C]//Guidance, Navigation and Control Conference (CGNCC).[S.l.]: IEEE, 2014: 1624-1629. |
| [13] |
SCHIERMAN J D, WARD D G, HULL J R, et al.
Integrated adaptive guidance and control for re-entry vehicles with flight test results[J]. Journal of Guidance Control & Dynamics, 2004, 27(6): 975–988.
|
| [14] |
TIAN B, FAN W, ZONG Q, et al.
Nonlinear robust control for reusable launch vehicles in reentry phase based on time-varying high order sliding mode[J]. Journal of the Franklin Institute, 2013, 350(7): 1787–1807.
DOI:10.1016/j.jfranklin.2013.04.022
|
| [15] |
YAN H, TAN S, HE Y.
A small-gain method for integrated guidance and control in terminal phase of reentry[J]. Acta Astronautica, 2017, 132: 282–292.
DOI:10.1016/j.actaastro.2016.12.027
|
| [16] |
赵暾, 王鹏, 刘鲁华, 等.
带落角约束的高超声速飞行器一体化制导控制[J]. 控制理论与应用, 2015, 32(7): 925–933.
ZHAO Tun, WANG Peng, LIU Luhua, et al. Integrated guidance and control with terminal angular constraint for hypersonic vehicles[J]. Control Theory & Applications, 2015, 32(7): 925–933. |
| [17] |
孙向宇, 晁涛, 王松艳, 等.
考虑通道耦合因素的制导控制一体化设计方法[J]. 宇航学报, 2016, 37(8): 936–945.
DOI:10.3873/j.issn.1000-1328.2016.08.006 SUN Xiangyu, CHAO Tao, WANG Songyan, et al. Integrated guidance and control design method considering channel coupling[J]. Journal of Astronautics, 2016, 37(8): 936–945. DOI:10.3873/j.issn.1000-1328.2016.08.006 |
| [18] |
WANG J H, LIU L H, ZHAO T, et al.
Integrated guidance and control for hypersonic vehicles in dive phase with multiple constraints[J]. Aerospace Science & Technology, 2016, 53: 103–115.
|
| [19] |
王建华, 刘鲁华, 汤国建.
高超声速飞行器俯冲段制导与姿控系统设计[J]. 宇航学报, 2016, 37(8): 964–973.
DOI:10.3873/j.issn.1000-1328.2016.08.009 WANG Jianhua, LIU Luhua, TANG Guojian. Guidance and attitude control system design for hypersonic vehicle in dive phase[J]. Journal of Astronautics, 2016, 37(8): 964–973. DOI:10.3873/j.issn.1000-1328.2016.08.009 |
| [20] |
ZHU J, LIU L, TANG G, et al.
Optimal diving maneuver strategy considering guidance accuracy for hypersonic vehicle[J]. Acta Astronautica, 2014, 104(1): 231–242.
DOI:10.1016/j.actaastro.2014.07.026
|
| [21] |
BURKEN J J, LU P, WU Z L, et al.
Two reconfigurable flight-control design methods:Robust servomechanism and control allocation[J]. Journal of Guidance Control Dynamics, 2012, 24(3): 482–493.
|
| [22] |
JIANG B, XU D Z, SHI P, et al.
Adaptive neural observer-based backstepping fault tolerant control for near space vehicle under control effector damage[J]. IET Control Theory and Application, 2014, 8(9): 658–666.
DOI:10.1049/iet-cta.2013.0404
|
| [23] |
XU D Z, JIANG B, SHI P.
Robust NSV fault tolerant control system design against actuator faults and control surface damage under actuator dynamics[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5919–5928.
DOI:10.1109/TIE.2015.2450714
|
| [24] |
POLYCARPOU M M, IOANNOU P A.
A robust adaptive nonlinear control design[J]. Automatica, 1996, 32(3): 423–427.
DOI:10.1016/0005-1098(95)00147-6
|
| [25] |
王立新, 王迎军.
模糊系统与模糊控制教程[M]. 北京: 清华大学出版社, 2003: 81-255.
|
| [26] |
YAO B, TOMIZUKA M.
Adaptive robust control of MIMO nonlinear systems in semi-strict feedback forms[J]. Automatica, 2001, 37(9): 1305–1321.
DOI:10.1016/S0005-1098(01)00082-6
|
| [27] |
KHALIL H K.
Adaptive output feedback control of nonlinear systems represented by input-output models[J]. Automatic Control IEEE Transactions on, 1996, 41(2): 177–188.
DOI:10.1109/9.481517
|
| [28] |
LU P, HANSON J M.
Entry guidance for the X-33 vehicle[J]. Journal of Guidance Control Dynamics, 1998, 35(3): 342–349.
|
| [29] |
杨鹏宇.高超声速飞行器再入轨迹优化与容错制导研究[D].南京: 南京航空航天大学, 2017.
YANG Pengyu. Research on trajectory optimization and fault-tolerant guidance for reentry hypersonic vehicles[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017. |
 2018, Vol. 50
2018, Vol. 50


