不断地提高收益水平是航空公司永远不变的追求。提高收益水平可从生产和销售两部分出发。从生产出发，就是不断提高营运水平，尤其是在无法按计划进行生产情况下的优化运营能力^[1-2]；从销售出发，就是将产品的销售最优化，尤其是机票的销售最优化。本文主要研究后一种问题。航空机票是一种易逝性产品，具有生产消费的同时性特点，在飞机起飞时没有卖掉的机票残值为零。因此，航空公司面临着要在一定的时期内销售固定数量的机票，实现总收益的最大化这一问题。对于旅客来说，由于飞行目的不同，导致对航班时间、价格以及服务等的要求存在差异，因此，对产品的支付意愿就会不同。航空公司若能合理地进行市场细分，尽可能地根据每类客户的支付意愿索要价格，就能避免收益的不必要流失。实际上，航空收益管理就是从差别定价的思想出发，在合适的时间，以合适的价格将适当数量的产品卖给合适的顾客。理论上将定价问题作为收益管理的一部分进行研究是从20世纪90年代开始的。

大量关于动态定价的研究是基于市场相对垄断的情况下对单航班机票定价问题的分析和探讨，也有一部分学者将竞争因素考虑在内进行定价研究。Gallego等人^[3]最早针对有限销售时间段内的易逝性产品定价问题进行了建模分析，并在需求函数为指数函数的条件下得出了最优解，在一般需求函数的条件下确定了期望收益的上界值。Gallego等人^[4]研究了可以用于网络收益管理中的多品种动态定价模型。Feng等人^[5]基于一般需求函数建立了两等级票价结构模型，并得出了最优定价策略。随后，Feng等人^[6]在两级票价结构模型中考虑了风险因素，并证明了模型能够得到准确的分析解。Feng等人^[7]拓展了两等级票价结构模型，并且允许价格可逆向运动，在此基础上提出了连续时间下的多等级票价结构的动态定价模型。Zhao等人^[8]对非齐次需求下易逝性产品的动态定价问题进行了研究，并且给出了在一定库存水平下，最优价格随时间递减的一个充分条件，证明了阈值控制的最优性。此外，有关研究成果还包括Chen等人^[9]的离散时间模型，Dimitris等人^[10]的应用于航空收益管理的多资源多产品的离散时间动态定价模型，以及Lin等人^[11]考虑竞争因素所构建的离散时间动态定价博弈模型。

在国内，施飞等人^[12]研究了随时间变化的折扣票定价问题，给出了相应的定价模型，通过模型能够得到各种折扣机票的销售时间段。周蔷等人^[13]从价格控制市场需求的角度出发，建立了考虑No-Show的兼顾多航段机票定价模型。许洪等人^[14]综合旅客订座累积概率分布特点, 以提前座位时间天数和成本为主要变量, 建立了航空公司机票定价动态模型。罗利等人^[15]基于竞争的市场环境，应用随机控制和博弈两种理论, 建立了基于连续时间的两家航空公司、两个航班情况下的两级价格动态定价模型, 探讨了模型求解的方法及相关性质。高金敏等人^[16]基于超模博弈理论建立了机票定价与舱位控制联合决策模型。李晓花等人^[17]运用随机过程理论和最大凹向包络原理探讨了动态定价与舱位控制的统一模型。罗利等人^[18]应用随机控制理论，建立了基于连续时间的两个平行航班动态定价模型，并对最优策略的相关性质进行了证明，得到了最优动态定价综合策略。

以上关于收益管理中动态定价的研究成果，无论是垄断环境还是竞争环境，都没有深入研究和探讨旅客需求强度受时间影响的定价问题。本文在Gallego和Ryzin(1994)^[3]连续动态定价模型研究的基础上，考虑旅客时变需求，深入分析了时变需求下的动态定价模型所具有的性质和满足的相关定理，主要包括最优期望收益和最优价格分别关于剩余机票数量和剩余销售时间的单调性质和凹凸性质等，并且进行了详细的证明。此外，针对模型的求解问题，分别针对两种票价等级和多种票价等级的情况提出了有效的离散定价策略来近似求解，通过算例进行了验证分析。

1 定价模型结构

假设航空公司有N张机票，要求在有限时间段[0, T]内销售，在这个过程中，航空公司需要采用一系列价格控制策略，通过调控旅客需求来实现收益最大化。

根据收益管理中有关定价问题研究的一般假设，设定s时刻的价格为p_s，对应的需求强度为λ_s=λ(p_s, s)，并且λ(p, t)是关于价格p的严格单调减函数；收益率r=pλ(p, t)，是关于价格p的连续有界凹函数。

定义N_s为截至s时刻航空公司售出的机票数，若dN_s=1，表示有一个订座请求被接受，在不考虑取消订座的情况下，航空公司收益为p_s。

定义价格集合：$P \subset \left( {0, \infty } \right) $，并且满足$ {\rm{li}}{{\rm{m}}_{p \to \infty }}\lambda \left( {p, t} \right) = 0, {\rm{li}}{{\rm{m}}_{p \to \infty }}p\lambda \left( {p, t} \right) = 0$，当机票售完时，p=∞。旅客需求密度集合为：$\mathit{\Lambda} = \left\{ {\lambda \left( {p, t} \right):p \in P} \right\} $；U表示所有的价格策略集合，并且满足：$\int_0^t {{\rm{d}}{N_s} \le n} $。

根据上述模型符号的定义和假设可以得到，对于任一价格策略u ∈U，航空公司在周期t(t>0)内销售n(n>0)张机票所获得的最大期望收益为

$ \pi \left( {n,t} \right) = \mathop {\sup }\limits_{u \in U} {E_u}\left[ {\int_0^t {{p_s}{\rm{d}}{N_s}} } \right] $

(1)

并且满足：$\pi \left( {n, 0} \right) = 0, \forall n, \pi \left( {0, t} \right) = 0, \forall t $。

如果设定价格为p(λ)，相应的旅客需求强度为λ(p, t)，那么航空公司在接下来一个极小的时间段Δt内卖出一张机票的概率为λΔt，没有卖出机票的概率为1－λΔt。根据最优性原理得到

$ \begin{array}{*{20}{c}} {\pi \left( {n,t} \right) = \mathop {\sup }\limits_p \left[ {\lambda \Delta \left( t \right)\left( {p\left( \lambda \right) + \pi \left( {n - 1,t - \Delta t} \right)} \right) + } \right.}\\ {\left. {\left( {1 - \lambda \Delta t} \right)\pi \left( {n,t - \Delta t} \right) + o\left( {\Delta t} \right)} \right]} \end{array} $

(2)

当Δt→0时得到该问题的哈密尔顿-雅克比方程

$ \begin{array}{l} \frac{{\partial \pi \left( {n,t} \right)}}{{\partial t}} = \mathop {\sup }\limits_p \left[ {\lambda p\left( \lambda \right) - \lambda \left( {\pi \left( {n,t} \right) - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\pi \left( {n - 1,t} \right)} \right)} \right]\;\;\;\;\;\;\forall n \ge 1,\forall t > 0 \end{array} $

(3)

边界条件为

$ \pi \left( {n,0} \right) = 0,\forall n;\pi \left( {0,t} \right) = 0,\forall t $

定义边际期望收益

$ \Delta \pi \left( {n,t} \right) = \pi \left( {n,t} \right) - \pi \left( {n - 1,t} \right) $

则式(3)可写为

$ \begin{array}{*{20}{c}} {\frac{{\partial \pi \left( {n,t} \right)}}{{\partial t}} = \mathop {\sup }\limits_p \left[ {\lambda \left( {p,t} \right)\left( {p - \Delta \pi \left( {n,t} \right)} \right)} \right]}\\ {\forall n \ge 1,\forall t > 0} \end{array} $

(4)

定义

$ {Y^t}\left( {p,n,t} \right) = \lambda \left( {p,t} \right)\left( {p - \Delta \pi \left( {n,t} \right)} \right) $

(5)

则Y^t(p, n, t)是关于价格p的连续凹函数。最优定价为

$ {p^t}\left( {n,t} \right) = \arg \mathop {\max }\limits_p {Y^t}\left( {p,n,t} \right) $

(6)

2 相关性质和证明

定理1   最优期望收益分别关于变量n与t单调递增，并且是n的凹函数。

最优期望收益分别关于n与t单调递增这一性质的证明可参考Gallego, Ryzin(1994) ^[3]，关于n的凹凸性质证明如下。

证明

采用数学归纳法证明最优期望收益是变量n的凹函数。

根据式(4)可得

$ \begin{array}{l} \frac{{\partial \pi \left( {n + 1,t} \right)}}{{\partial t}} = \lambda \left( {{p^t}\left( {n + 1,t} \right),t} \right)\left[ {{p^t}\left( {n + 1,t} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\Delta \pi \left( {n + 1,t} \right)} \right] \end{array} $

(7)

$ \begin{array}{l} \frac{{\partial \pi \left( {n,t} \right)}}{{\partial t}} \ge \lambda \left( {{p^t}\left( {n + 1,t} \right),t} \right)\left[ {{p^t}\left( {n + 1,t} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\Delta \pi \left( {n,t} \right)} \right] \end{array} $

(8)

由式(7，8)得

$ \frac{{\partial \Delta \pi \left( {n + 1,t} \right)}}{{\partial t}} \le - \lambda \left( {{p^t}\left( {n + 1,t} \right),t} \right){\Delta ^2}\pi \left( {n + 1,t} \right) $

(9)

同样地

$ \begin{array}{l} \frac{{\partial \pi \left( {n - 1,t} \right)}}{{\partial t}} = \lambda \left( {{p^t}\left( {n - 1,t} \right),t} \right)\left[ {{p^t}\left( {n - 1,t} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\Delta \pi \left( {n - 1,t} \right)} \right] \end{array} $

(10)

$ \begin{array}{l} \frac{{\partial \pi \left( {n,t} \right)}}{{\partial t}} \ge \lambda \left( {{p^t}\left( {n - 1,t} \right),t} \right)\left[ {{p^t}\left( {n - 1,t} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\Delta \pi \left( {n,t} \right)} \right] \end{array} $

(11)

由式(10，11)得

$ \frac{{\partial \Delta \pi \left( {n,t} \right)}}{{\partial t}} \le - \lambda \left( {{p^t}\left( {n - 1,t} \right),t} \right){\Delta ^2}\pi \left( {n,t} \right) $

(12)

由式(9—12)得

$ \begin{array}{l} \frac{{\partial {\Delta ^2}\pi \left( {n + 1,t} \right)}}{{\partial t}} \le - \lambda \left( {{p^t}\left( {n + 1,t} \right),t} \right){\Delta ^2}\pi \left( {n + 1,t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \left( {{p^t}\left( {n - 1,t} \right),t} \right){\Delta ^2}\pi \left( {n,t} \right) \end{array} $

(13)

当n=1时，分别根据式(9)和式(12)得

$ \frac{{\partial \Delta \pi \left( {2,t} \right)}}{{\partial t}} \le - \lambda \left( {{p^t}\left( {2,t} \right),t} \right){\Delta ^2}\pi \left( {2,t} \right) $

(14)

$ \frac{{\partial \Delta \pi \left( {1,t} \right)}}{{\partial t}} \ge \frac{{\partial \left[ {\pi \left( {1,t} \right) - \pi \left( {0,t} \right)} \right]}}{{\partial t}} = \frac{{\partial \pi \left( {1,t} \right)}}{{\partial t}} \ge 0 $

(15)

因此

$ \frac{{\partial {\Delta ^2}\pi \left( {2,t} \right)}}{{\partial t}} \le - \lambda \left( {{p^t}\left( {2,t} \right),t} \right){\Delta ^2}\pi \left( {2,t} \right) $

(16)

两边同乘$ {\rm{exp}}\left( {\int_0^t {[\lambda ({p^s}\left( {2, s} \right), s)]{\rm{d}}s)} } \right)$得$\frac{{\partial {\Delta ^2}\pi \left( {2, {\rm{ }}t} \right)}}{{\partial t}}{\rm{exp}}\left( {\int_0^t {[\lambda ({p^s}\left( {2, s} \right), s)]{\rm{d}}s} } \right) + \lambda ({p^t}\left( {2, t} \right), t)*{\rm{ }}{\Delta ^2}\pi \left( {2, t} \right){\rm{exp}}\left( {\int_0^t {[\lambda ({p^s}\left( {2, s} \right), s)]{\rm{d}}s} } \right) \le 0 $即

$ \frac{{\partial \left( {\exp \left( {\int_0^t {\left[ {\lambda \left( {{p^s}\left( {2,s} \right),s} \right)} \right]{\rm{d}}s} } \right){\Delta ^2}\pi \left( {2,t} \right)} \right)}}{{\partial t}} \le 0 $

(17)

所以，${\rm{exp}}\left( {\int_0^t {[\lambda ({p^s}\left( {2, s} \right), s)]{\rm{d}}s} } \right){\Delta ^2}\pi \left( {2, t} \right) $是关于t的递减函数。因此得到：$ {\rm{exp}}\left( {\int_0^t {[\lambda ({p^s}\left( {2, s} \right), s)]{\rm{d}}s} } \right){\Delta ^2}\pi \left( {2, t} \right) \le {\rm{exp}}\left( {\int_0^0 {[\lambda ({p^s}\left( {2, s} \right), s)]{\rm{d}}s} } \right){\Delta ^2}\pi \left( {2, 0} \right) = 0$，进而推出：Δ²π(2, t)≤0。

所以，当n=1时，定理是成立的。

假设当n=k时定理成立，即Δ²π(k, t)≤0，那么根据式(13)可以得到

$ \begin{array}{l} \frac{{\partial {\Delta ^2}\pi \left( {k + 1,t} \right)}}{{\partial t}} \le - \lambda \left( {{p^t}\left( {k + 1,t} \right),t} \right) * \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\Delta ^2}\pi \left( {k + 1,t} \right) \end{array} $

(18)

利用与式(16，17)同样的分析方法得到Δ²π(k+1, t)≤0，即n=k+1时，定理成立。

综上所述，π(n, t)是关于n的凹函数，定理1得以证明。

命题1   边际期望收益Δπ(n, t)关于n单调递减，关于t单调递增。

在旅客需求只受价格影响的动态定价模型中，最优收益函数分别是n与t的单调递增凹函数，并且边际期望收益Δπ(n, t)关于n单调递减，关于t单调递增。

而考虑时变需求时，最优收益函数仍然是n的凹函数，所以，边际期望收益关于n的递减性质依旧成立。根据式(12)得$ \frac{{\partial {\Delta ^2}\pi \left( {2, {\rm{ }}t} \right)}}{{\partial t}} \ge - \lambda ({p^t}\left( {n - 1, t} \right), t){\Delta ^2}\pi \left( {n, t} \right) \ge 0$，所以边际期望关于t单调递增的性质仍然成立。

命题2  最优收益关于t的凹凸性取决于时间对需求强度的影响。

证明

对任意t < t′, t, t′∈[0, T]，根据式(4)可得

$ \begin{array}{l} \frac{{\partial \pi \left( {n,t'} \right)}}{{\partial t'}} = \mathop {\sup }\limits_p \left[ {\lambda \left( {p,t'} \right)\left( {p - \Delta \pi \left( {n,t'} \right)} \right)} \right] \ge \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \left( {{p^t}\left( {n,t} \right),t'} \right)\left( {{p^t}\left( {n,t} \right) - \Delta \pi \left( {n,t'} \right)} \right) \end{array} $

(19)

$ \frac{{\partial \pi \left( {n,t} \right)}}{{\partial t}} = \lambda \left( {{p^t}\left( {n,t} \right),t} \right)\left( {{p^t}\left( {n,t} \right) - \Delta \pi \left( {n,t} \right)} \right) $

(20)

由式(19，20)得

$ \begin{array}{l} \frac{{\partial \pi \left( {n,t'} \right)}}{{\partial t'}} - \frac{{\partial \pi \left( {n,t} \right)}}{{\partial t}} \ge \lambda \left( {{p^t}\left( {n,t} \right),t'} \right)\left[ {{p^t}\left( {n,t} \right) - } \right.\\ \left. {\Delta \pi \left( {n,t'} \right)} \right] - \lambda \left( {{p^t}\left( {n,t} \right),t} \right)\left[ {{p^t}\left( {n,t} \right) - \Delta \pi \left( {n,t} \right)} \right] \end{array} $

(21)

只有式(21)右边项大于等于0，即$\frac{{\lambda ({p^t}\left( {n, t} \right), t\prime )}}{{\lambda ({p^t}\left( {n, t} \right), t)}} \ge \frac{{{p^t}\left( {n, t} \right) - {\rm{ }}\Delta \left( {n, t} \right)}}{{{p^t}\left( {n, t} \right) - \Delta \left( {n, t\prime } \right)}} $时，最优收益函数才是关于t的凹函数。若λ(p, t)=λ(p)F(t)，则需要满足

$ \frac{{F\left( {t'} \right)}}{{F\left( t \right)}} \ge \frac{{{p^t}\left( {n,t} \right) - \Delta \left( {n,t} \right)}}{{{p^t}\left( {n,t} \right) - \Delta \left( {n,t'} \right)}} $

(22)

因此，在考虑时变需求的情况下，最优收益是t的凹函数这一性质已不成立。

定理2   最优价格p^t(n, t)关于n单调递减，关于t单调递增的性质已不成立。

在旅客需求只受价格影响的动态定价模型中，最优价格关于n单调递减，关于t单调递增。考虑旅客时变需求时，最优价格p^t(n, t)关于n单调递减的证明如下。

证明(1)

已知λ(p, t)是关于p的减函数，以及最优收益是关于n的凹函数，那么对于任意价格p>p^t (n, t)，能够得到

$ \begin{array}{l} {Y^t}\left( {{p^t}\left( {n,t} \right),n + 1,t} \right) + {Y^t}\left( {p,n,t} \right) - {Y^t}\left( {p,n + 1,} \right.\\ \left. t \right) - {Y^t}\left( {{p^t}\left( {n,t} \right),n,t} \right) = {Y^t}\left( {{p^t}\left( {n,t} \right),n + 1,t} \right) - \\ {Y^t}\left( {{p^t}\left( {n,t} \right),n,t} \right) + {Y^t}\left( {p,n,t} \right) - {Y^t}\left( {p,n + 1,t} \right) = \\ - \lambda \left( {{p^t}\left( {n,t} \right),t} \right){\Delta ^2}\pi \left( {n + 1,t} \right) + \lambda \left( {p,t} \right){\Delta ^2}\pi \left( {n + 1,t} \right) = \\ - \left( {\lambda \left( {p\left( {n,t} \right),t} \right) - \lambda \left( {p,t} \right)} \right){\Delta ^2}\pi \left( {n + 1,t} \right) \ge 0 \end{array} $

(23)

因此

$ \begin{array}{l} {Y^t}\left( {{p^t}\left( {n,t} \right),n + 1,t} \right) - {Y^t}\left( {p,n + 1,t} \right) \ge {Y^t}\left( {{p^t}\left( {n,} \right.} \right.\\ \;\;\;\;\;\;\;\left. {\left. t \right),n,t} \right) - {Y^t}\left( {p,n,t} \right) \end{array} $

(24)

根据p^t(n, t)的定义得式(24)不等式右边大于0，所以：${Y^t}({p^t}\left( {n, t} \right), n + 1, t) - {Y^t}\left( {p, n + 1, t} \right) \ge 0 $。再根据p^t(n+1, t)的定义得：p^t(n+1, t)≤p^t(n, t)。所以最优价格关于n单调递减。

接下来具体证明最优价格关于t的单调性。

证明(2)

根据式(5)，若最优价格p^t(n, t)关于t单调递增，那么，对任一s < t，p < p^s(n, s)，须满足：$ {Y^t}({p^s}\left( {n, s} \right), n, t) > {Y^t}\left( {p, n, t} \right)$。

根据p^s(n, s)的定义${Y^s}\left( {p, n, s{\rm{ }}} \right)s\left( {{p^s}\left( {n, s} \right), n, s} \right) $，通过化简得到

$ \Delta \pi \left( {n,s} \right) \ge \frac{{\lambda \left( {p,s} \right)p - \lambda \left( {{p^s}\left( {n,s} \right),s} \right){p^s}\left( {n,s} \right)}}{{\lambda \left( {p,s} \right) - \lambda \left( {{p^s}\left( {n,s} \right),s} \right)}} $

(25)

由于边际期望收益Δπ(n, t)是关于t的增函数，因此Δπ(n, t)≥Δπ(n, s)。只有当$ \frac{{\lambda \left( {p, t} \right)p - \lambda ({p^s}\left( {n, s} \right), t){p^s}\left( {n, s} \right)}}{{\lambda \left( {p, t} \right) - \lambda ({p^s}\left( {{\rm{ }}n, s} \right), t)}}$关于t递减时，才能得到

$ \begin{array}{l} \Delta \pi \left( {n,t} \right) \ge \Delta \pi \left( {n,s} \right) > \\ \;\;\;\;\;\;\;\frac{{\lambda \left( {p,s} \right)p - \lambda \left( {{p^s}\left( {n,s} \right),s} \right){p^s}\left( {n,s} \right)}}{{\lambda \left( {p,s} \right) - \lambda \left( {{p^s}\left( {n,s} \right),s} \right)}} \ge \\ \;\;\;\;\;\;\;\frac{{\lambda \left( {p,t} \right)p - \lambda \left( {{p^s}\left( {n,s} \right),t} \right){p^s}\left( {n,s} \right)}}{{\lambda \left( {p,t} \right) - \lambda \left( {{p^s}\left( {n,s} \right),t} \right)}} \end{array} $

(26)

即

$ \Delta \pi \left( {n,t} \right) \ge \frac{{\lambda \left( {p,t} \right)p - \lambda \left( {{p^s}\left( {n,s} \right),t} \right){p^s}\left( {n,s} \right)}}{{\lambda \left( {p,t} \right) - \lambda \left( {{p^s}\left( {n,s} \right),t} \right)}} $

(27)

因此得到：${Y^t}\left( {p\left( {n, s} \right), n, t} \right) > {Y^t}\left( {p, n, t} \right) $，进而推出$ {p^t}\left( {n, t} \right) \ge {p^s}\left( {n, s} \right)$。所以，最优价格关于t单调递增的性质已不成立，但根据以上证明可以得出：$ \frac{{\lambda \left( {p, t} \right)p - \lambda ({p^s}\left( {n, s} \right), t){p^s}\left( {n, s} \right)}}{{\lambda \left( {p, t} \right) - \lambda ({p^s}\left( {n, s} \right), t)}}$关于t递减是最优价格p^t(n, t)关于t单调递增的一个充分条件。

综合以上分析，定理2得以证明。

3 离散定价机制 3.1 非时变需求下的离散定价

上述所讨论的基于连续时间的完全差别定价模型，在实际应用时需要对机票销售情况进行实时监控，不断进行动态调整，所以会大大增加管理成本，并且价格的不断波动会使顾客产生“不公平感”，降低顾客满意度。因此，根据以上分析的动态定价模型所具有的性质特点，考虑实施有效的定价机制，即离散定价机制，既能保证航空公司总的收益水平，降低管理成本，又能更好地应对旅客需求的波动。

本节考虑机票价格集合为离散集合的情况，假设航空公司在机票预售期[0, T]内以K种不同的价格销售N张机票，可行价格集合为P={p₁, p₂, …，p_K}，其中p₁ < p₂ < … < p_K。

定义λ_k为票价p_k对应的需求强度，满足$ {\lambda _1} > {\lambda _2} > \ldots > {\lambda _K};{r_k} = {p_k}{\lambda _k}$为票价p_k所对应的收益率，满足r₁>r₂>…>r_k。

定理3  在价格集合P为离散的情况下，对于任一状态(n, t)，存在一个序列$ {z^0}\left( n \right) = 0 \le {z^1}\left( n \right) \le \ldots {z^K}\left( n \right) = \infty $，当${z^{k - 1}}\left( n \right) < t < {z^k}\left( n \right) $时，最优价格为p_k。此外，z^k(n)关于变量n单调递增。

证明

定义$ {z^k}\left( n \right) = {\rm{sup}}\{ t:p\left( {n, t} \right) \le {p_k}\} \left( {k = 1, 2, \ldots , K - 1} \right)$，并且$ {z^0}\left( n \right) = 0, {z^K}\left( n \right) = {\rm{ }}\infty $。由于最优价格p(n, t)关于t单调递增，所以z^k(n)关于k单调递增。当$ {z^{k - 1}}\left( n \right) < t < {z^k}\left( n \right)$时，最优价格p(n, t)=p_k。此外，由于最优价格p(n, t)关于n单调递减，根据z^k(n)的定义可得z^k(n)关于n单调递增。

3.2 时变需求下的离散定价

对于时变需求下的离散定价问题，当最优价格关于t单调递增时，定理3的性质才成立。

在考虑时变需求时，旅客订票过程有两个特点：首先，旅客总需求是不确定的；其次，各票价等级的旅客到达强度是不同的，并且随时间不断变化。基于这两个特点，定义旅客需求强度为

$ \lambda \left( {p,s} \right) = \lambda \left( p \right)f\left( s \right) $

(28)

式中：s表示已售票时间，f(s)表示一个连续凹函数。那么，旅客到达便为一个非时齐泊松过程，这也是航空收益管理中对旅客到达最常用的一种模拟方式。本文定义f(s)为高斯分布，其分布函数为连续凹函数，在机票销售中期附近达到顶峰，符合实际旅客订票的一般规律。

定义：$u = F\left( s \right) = \int_0^s {f{\rm{ }}\left( z \right){\rm{d}}z, 0 \le s \le t} $，并且对于任一s′ < s，令u′=F(s′), u=F(s)，那么可以得到

$ \begin{array}{l} \int_{s'}^s {\lambda \left( {p,z} \right){\rm{d}}z} = \lambda \left( p \right)\int_{s'}^s {f\left( z \right){\rm{d}}z} = \lambda \left( p \right)\left[ {F\left( s \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {F\left( {s'} \right)} \right] = \lambda \left( p \right)\left( {u - u'} \right) = \int_{u'}^u {\lambda \left( p \right){\rm{d}}v} \end{array} $

(29)

此时，旅客到达便转化为时齐泊松分布的情况。

4 模型求解和算例分析 4.1 确定性求解方法

为求解所建立的连续时间动态定价模型，本文采用确定性的离散定价方法来近似求解，首先将动态定价模型转化为确定性模型。对于一定的机票数量x，在销售期[0, t]内获得的最大期望收益为

$ \begin{array}{*{20}{c}} {{\pi ^D}\left( {n,t} \right) = \mathop {\max }\limits_{\lambda \left( {{p_s},s} \right)} \int_0^t {r\left( {\lambda \left( {{p_s},s} \right)} \right){\rm{d}}s} }\\ {\forall \int_0^t {\lambda \left( {{p_s},s} \right){\rm{d}}s} \le x,\lambda \left( {{p_s},s} \right) \in \mathit{\Lambda }} \end{array} $

(30)

根据连续性定价问题的描述，针对离散定价情况，定义

$ {\lambda _0} = \infty ,{\lambda _K} = 0,{r_0} = {r_K} = 0 $

(31)

(1) 两等级票价定价策略

根据Gallego和Ryzin(1994)的研究^[3]，对确定性定价模型求解所得的收益结果，是实际所得收益的上限，研究同时提出了一种近似最优的两等级票价定价机制。本文在该研究的基础上，通过考虑旅客组合需求均值，将两等级票价定价策略扩展到多等级票价的情况。

定义t_k为定价p_k的时间段，那么

$ \begin{array}{*{20}{c}} {{t_k} = \int_0^t {\mathit{Pr}\left( {{p_s} = {p_k}} \right){\rm{d}}s} }&{k = 1,2, \cdots ,K} \end{array} $

(32)

如果在时刻s定价为p_k，那么Pr(p_s=p_k)=1，反之为0。此时，离散定价模型为一个线性规划模型。

对于任一状态(n, t)，若k^*满足λ_k^*+1t < n≤λ_k^*t，那么两等级票价的定价策略为

$ \forall j \notin \left\{ {{k^ * },{k^ * } + 1} \right\},{t_j} = 0 $

(33)

$ {t_{{k^ * }}} = \frac{{n - {\lambda _{{k^ * } + 1}}t}}{{{\lambda _{{k^ * }}} - {\lambda _{{k^ * } + 1}}}},{t_{{k^ * } + 1}} = \frac{{{\lambda _{{k^ * }}}t - n}}{{{\lambda _{{k^ * }}} - {\lambda _{{k^ * } + 1}}}} $

(34)

当k^*=0时，t_k=0, t_k+1=t；当k^*=K时，${t_k} = \frac{n}{{{\lambda _K}}}, {t_{k + 1}} = 0 $。

同样地，得到时变需求下的两票价等级定价策略：对于任一状态(n, t)，若k^*满足${\lambda _{_{k^*} + 1}}F\left( t \right) < n \le {\lambda _{{k^*}}}F\left( t \right) $，那么定价为p_k^*和p_k^*+1的时间满足式(35)，通过求反函数得到具体的定价时间段。

$ {u_{{k^ * }}} = \frac{{n - {\lambda _{{k^ * } + 1}}F\left( t \right)}}{{{\lambda _{{k^ * }}} - {\lambda _{{k^ * } + 1}}}},{u_{{k^ * } + 1}} = \frac{{{\lambda _{{k^ * }}}F\left( t \right) - n}}{{{\lambda _{{k^ * }}} - {\lambda _{{k^ * } + 1}}}} $

(35)

$ {t_{{k^ * }}} = \arg F\left( {{u_{{k^ * }}}} \right),{t_{{k^ * } + 1}} = \arg F\left( {{u_{{k^ * } + 1}}} \right) $

(36)

由式(35—36)可以看到，在航班容量和旅客总需求均值一定时，若考虑时变需求，那么各票价的定价时间完全取决于旅客到达模式分布，若旅客到达模式发生改变，定价时间也会相应地改变。

(2) 多等级票价定价策略

实际机票销售时，两种机票定价远远不能满足旅客的实际需求，因此，要结合不同的订座限制制定多种票价。令定价为p_k的时间段为

$ {t_k} = \frac{{\lambda _{k - 1}^ - - \lambda _k^ - - n_k^ - }}{{\lambda _{k - 1}^ - - {\lambda _k}}} $

(37)

式中：$t_k^ - $表示剩余给票价等级{1, 2, …, k}的销售时间段；$n_k^ - $为相应的机票数量，并且$ t_{k - 1}^ - = t_k^ - - {t_k}, n_{k - 1}^ - = n_k^ - - {\lambda _{k}}t{_k};\lambda _k^ - $为票价等级{1, 2, …, k}的旅客需求均值，并且$\lambda _k^ - = \frac{1}{k}\sum\limits_{j = 1}^k {{\lambda _j}} $。初始的机票数量和销售时间段分别为：$ n_K^ - = n, {\rm{ }}t_K^ - = t$。

这样，航空公司就能以k(k ≥2)种票价等级进行机票销售。但是前提是航空公司要通过价格大小的调整，使得$ {\lambda _{k}}t_k^ - < n_k^ - \le \lambda _{k - 1}^ - t_k^ - $成立。

考虑时变需求下的多等级票价定价策略，令定价为p_k的时间段满足

$ {u_k} = \frac{{\lambda _{k - 1}^ - F\left( {t_k^ - } \right) - n_k^ - }}{{\lambda _{k - 1}^ - - {\lambda _k}}} $

(38)

$ {t_k} = \arg F\left( {{u_k}} \right) $

(39)

式中：$ n_{k - 1}^ - = n_k^ - - {\lambda _k}{u_k}, t_{k - 1}^ - = t_k^ - - {t_k}$。只要满足条件${\lambda _k}F(t_k^ - ) <n_k^ - \le \lambda _{k - 1}^ - F\left( {t_k^ - } \right) $，该定价策略就有效。

4.2 算例分析

假设航空公司有n=300张机票在时间段[0, 360]内销售，各票价等级的价格和相应的需求强度如表 1，2中所示。考虑旅客时变需求时，假设旅客到达模式分布参数为(180, 20)，总需求均值为360。

表 1，2中的结果显示，对于只包含2种票价等级的情况，若不考虑旅客时变需求，航空公司应该在时间段[0, 207.3]内以价格p=400进行售票，在时间段(207.3, 360]内以价格p=1 000进行售票。若考虑旅客时变需求，航空公司应该在时间段[0, 183.8]内以价格p=400进行售票，在时间段(183.8, 360]内以价格p=1 000进行售票。

对于包含多种票价等级的情况，若不考虑旅客时变需求得到：航空公司应在时间段[0, 114.5]内以价格p=400进行售票，在时间段(114.5, 228.9]内以价格p=600进行售票，在时间段(228.9, 340.3]内以价格p=800进行售票，在时间段(340.3, 360]内以价格p= 1 000进行售票。若考虑旅客时变需求得到：航空公司应在时间段[0, 170.5]内以价格p=400进行售票，在时间段(170.5, 186.9]内以价格p=600进行售票，在时间段(186.9, 212]内以价格p=8 00进行售票，在时间段(212, 360]内以价格p=1 000进行售票。因此，考虑时间因素对旅客需求强度的影响时，定价策略会发生很大的改变。

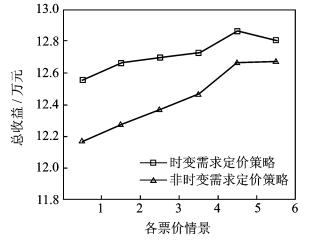
为进一步验证时变需求下动态定价模型的有效性，结合现实中机票的销售情况，假设某航班的全价票价格为p=1 000，在销售过程中可根据实际情况有选择的进行打折销售。全价票、9折、8折、7折、6折、5折、4折机票所对应的旅客需求强度为(0.2, 0.3, 0.42, 0.5, 0.64, 0.82, 2.8)。图 1中显示了6种情景下时变需求定价策略与非时变需求定价策略所能得到的总收益水平。横坐标中情景1对应只有一种折扣的情况，即机票只有全价票和3折机票；情景2对应的有全价票、6折和3折机票；情景3对应的有全价票、9折、6折和3折机票；情景4对应的有全价票、9折、6折、4折和3折机票；情景5对应的有全价票、9折、7折、6折、4折和3折机票；情景6对应的有全价票、9折、7折、6折、5折、4折和3折机票。

通过图 1可以看到，采用时变需求定价策略所得到的总收益要远高于非时变需求定价策略所得到的总收益，并且随着折扣数量的增加，即票价等级数量的增加，总收益也在不断提高。

5 结论

本文在连续动态定价模型基础上，考虑旅客时变需求，研究和分析了时变需求下动态定价模型所具有的性质和满足的相关定理，并进行了相应的证明。结果表明：在动态定价模型中考虑旅客时变需求时，最优期望收益关于剩余机票数量和剩余销售时间的单调递增性质没有变化，并且仍旧是剩余机票数量的凹函数，而关于剩余时间的凹凸性性质已不成立。最优票价关于剩余机票数量的单调递减性质没有变化，关于剩余时间的单调递增性质已不成立。期望边际收益关于剩余机票数量的递减性质和剩余销售时间的递增性质仍然成立。

此外，考虑到实施完全差别动态定价模型的成本问题，根据所分析的定价模型的性质特点，提出了现实有效的离散定价机制。分别针对两等级票价和多等级票价提出了相应的定价策略，通过算例验证和对比分析了时变需求与非时变需求下的定价策略的有效性，结果表明时变需求下的定价策略能带来更高的收益。

将来本研究可以拓展为考虑旅客取消行为，从而实施超售的情况，也可以考虑与舱位控制问题进行联合研究。