随着飞行器气动外形的新颖化、复杂化,传统的动稳定导数工程估算方法[1-2]已很难满足飞行器气动外形发展的需求,国内外许多学者采用强迫飞行器小幅度振荡开展基于非定常数值模拟获得动稳定导数方法的研究已取得了很大进展,且结果也比较准确[3-6],然而相对传统的工程估算方法效率太低,很难满足飞行器设计部门大批量计算的工程化应用需要。鉴于此,国内外学者在准定常方法和非定常频域方法提效方面也开展了相关研究[7-9]。目前准定常方法工程应用较广,计算效率较非定常方法有明显提升,但计算精度受所选步长的影响程度无法预先评估,需要丰富的应用经验。因此开展适用于复杂气动外形且与步长无关的动稳定导数快速计算方法研究仍然具有重要的现实意义。
本文基于笛卡尔网格和Euler方程基本流场解[10],通过Riemann不变量摄动,对旋转导数和角速度引起的物面法向速度构建摄动关系,发展了一种超声速旋转导数快速计算方法。利用国际动导数标准模型Basic Finner导弹[6-7, 11-12]进行算例验证,计算结果与试验数据、文献数据具有很好的一致性,展示出本文方法计算耗时少、精度高、工程实用性强,适合复杂气动外形飞行器的超声速旋转导数大批量快速计算。
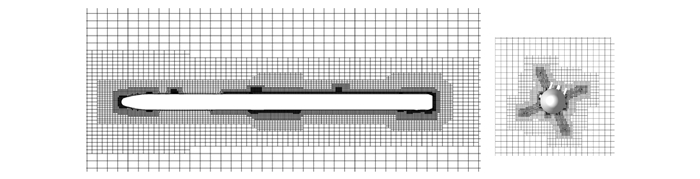
1 基于笛卡尔网格Euler方程的数值计算方法 1.1 网格生成本文采用八叉树结构的非结构直角网格对飞行器表面几何造型,一次性生成所需的空间网格[10],生成方法简单、省时、质量高且加密容易,见图 1。
|
图 1 某导弹空间笛卡尔网格 Figure 1 Space Cartesian meshes of missile |
1.2 控制方程
本文采用无黏假设下的Euler方程作为流场控制方程,其积分形式为
| $\frac{\partial }{{\partial t}}\iiint\limits_V \mathit{\boldsymbol{W}}{\text{d}}V + \iint\limits_{\partial V} {\mathit{\boldsymbol{F}}{\text{d}}\mathit{\boldsymbol{S}}{\text{ = 0}}}$ | (1) |
式中
| $\begin{array}{l} \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ {\rho v}\\ {\rho w}\\ E \end{array}} \right],\;\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\rho u}&{\rho v}&{\rho w}\\ {\rho {u^2} + p}&{\rho vu}&{\rho wu}\\ {\rho uv}&{\rho {v^2} + p}&{\rho wv}\\ {\rho uw}&{\rho vw}&{\rho {w^2} + p}\\ {uE + up}&{vE + vp}&{wE + wp} \end{array}} \right]\\ {\rm{d}}\mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{\rm{d}}{S_x}}\\ {{\rm{d}}{S_y}}\\ {{\rm{d}}{S_z}} \end{array}} \right] \end{array}$ | (2) |
式中:W为守恒量;F为通量张量;ρ为密度;p为压强;(u, v, w)为速度分量;dS为微面积向量,其大小为微面积,方向沿法向;E为总能量,表达式为
| $E = \frac{p}{{\gamma - 1}} + \frac{\rho }{2}\left( {{u^2} + {v^2} + {w^2}} \right)$ | (3) |
对于完全气体,比热比γ=1.4。三重积分对流场中任意体积V,二重积分对其表面积。
无因次化自由流的流动变量为:ρ∞=1,p∞=1,c∞2 = γ,E∞ =
|
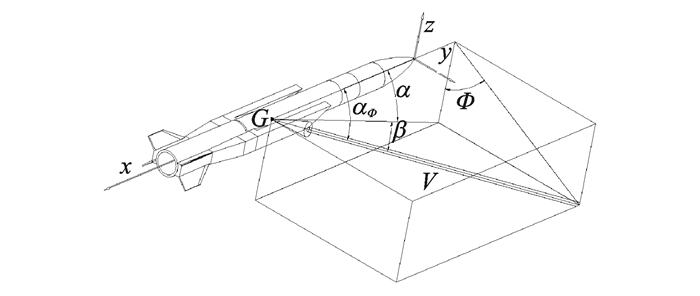
图 2 CFD计算坐标系 Figure 2 CFD coordinate system |
1.3 数值方法
本文采用具有迎风特性的Roe格式有限体积方法[13]进行数值计算。将积分型控制方程(1)应用到空间任意控制单元上进行离散,得到空间离散的控制方程为
| $V\frac{{{\text{d}}\mathit{\boldsymbol{W}}}}{{{\text{d}}t}} + \sum\limits_j {\mathit{\boldsymbol{F}}\Delta S = 0} $ | (4) |
式中:V为单元体积,W取单元中心的值,对单元的边界面进行求和。
单元边界面的通量F采用Roe的Riemann近似解算器[14]求解,同时采用守恒律单调迎风格式(Monotonic upwind scheme for conservation laws,MUSCL)插值方法并引入高阶通量限制器进行流场重构,以获得空间高阶精度。时间方向的推进采用三步Runge-Kutta方法,当时间推进到一定程度使得流场和气动参数不再随时间变化时,就得到定常的流场解和静态气动力和力矩系数。计算中边界条件分3种,分别为物面边界条件、对称面边界条件和远场边界条件。对于无黏绕流,物面边界条件是物面的法向速度为零;对称面同样无穿透,与物面一样处理;对远场边界,采用无反射边界条件(具体参见文献[10])。
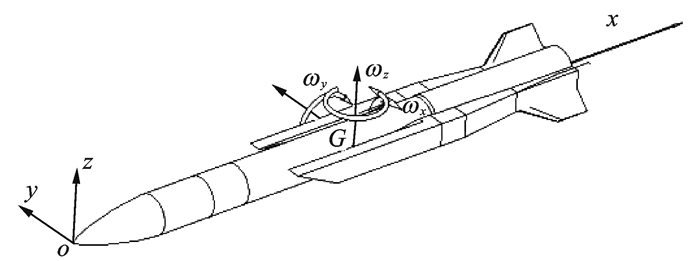
2 角速度扰动引起的物面扰动速度采用CFD计算中常用的体轴坐标系oxyz,原点位于飞行器端点,质心G(xg, yg, zg),角速度矢量ω(ωx, ωy, ωz)(见图 3),其中ωx,ωy,ωz分别为滚转、俯仰和偏航角速度。
|
图 3 角速度定义 Figure 3 Definition of angular velocities |
物面点P(x, y, z)距质心G(xg, yg, zg)的矢径r为
| $\mathit{\boldsymbol{r}} = \mathit{\boldsymbol{PG}} = \left( {\begin{array}{*{20}{c}} {x - {x_g}} \\ {y - {y_g}} \\ {z - {z_g}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\Delta x} \\ {\Delta y} \\ {\Delta z} \end{array}} \right)$ | (5) |
角速度ω(ωx, ωy, ωz)扰动引起的物面扰动速度为
| $\Delta \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{r}} = \left| {\begin{array}{*{20}{c}} i&j&k \\ {{\omega _x}}&{{\omega _y}}&{{\omega _z}} \\ {\Delta x}&{\Delta y}&{\Delta z} \end{array}} \right| = \left( {\begin{array}{*{20}{c}} {{\omega _y}\Delta z - {\omega _z}\Delta y} \\ {{\omega _z}\Delta x - {\omega _x}\Delta z} \\ {{\omega _x}\Delta y - {\omega _y}\Delta x} \end{array}} \right)$ | (6) |
取物面微元s(sx, sy, sz)上的单位外法向为
| $\mathit{\boldsymbol{n}} = \frac{\mathit{\boldsymbol{s}}}{{\left| \mathit{\boldsymbol{s}} \right|}} = \left\{ {\frac{{{s_x}}}{{{s_0}}},\frac{{{s_y}}}{{{s_0}}},\frac{{{s_z}}}{{{s_0}}}} \right\}$ |
其中s0表示s的模,那么,扰动速度ΔV在物面微元上的法向速度为
| $ {V_n} = \Delta \mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{n}} = \left( {{\omega _y}\Delta z - {\omega _z}\Delta y} \right)\frac{{{s_x}}}{{{s_0}}} + \\ \;\;\;\;\;\;\left( {{\omega _z}\Delta x - {\omega _x}\Delta z} \right)\frac{{{s_y}}}{{{s_0}}} + \left( {{\omega _x}\Delta y - {\omega _y}\Delta x} \right)\frac{{{s_z}}}{{{s_0}}} $ | (7) |
定义量纲为一的角速度
| ${{\bar \omega }_x} = \frac{{{\omega _x}{l_x}}}{{{V_\infty }}},{{\bar \omega }_y} = \frac{{{\omega _y}{l_y}}}{{{V_\infty }}},{{\bar \omega }_z} = \frac{{{\omega _z}{l_z}}}{{{V_\infty }}}$ | (8) |
式中:带上画线代表量纲为一的量,其中lx,ly,lz分别为ωx,ωy,ωz的参考长度。式(7)可进一步改写为量纲为一的形式,注意速度等流动量沿用Euler方程求解时的参考量量纲一化,式(7)最终可改写为
| $ {{\bar V}_n} = \sqrt \gamma M{a_\infty }\left[ {\left( {{{\bar \omega }_y}\frac{{\Delta z}}{{{l_y}}} - {{\bar \omega }_z}\frac{{\Delta y}}{{{l_z}}}} \right)\frac{{{s_x}}}{{{s_0}}}} \right. + \\ \;\;\;\;\;\;\;\left( {{{\bar \omega }_z}\frac{{\Delta x}}{{{l_z}}} - {{\bar \omega }_x}\frac{{\Delta z}}{{{l_x}}}} \right)\frac{{{s_y}}}{{{s_0}}} + \left. {\left( {{{\bar \omega }_x}\frac{{\Delta y}}{{{l_x}}} - {{\bar \omega }_y}\frac{{\Delta x}}{{{l_y}}}} \right)\frac{{{s_z}}}{{{s_0}}}} \right] $ | (9) |
速度的改变必然会引起物面压强等流动量的改变。
3 简单波修正法 3.1 简单波修正概念根据物面法向一维非定常Euler方程的特征理论分析,可知飞行器因角速度扰动,物面扰动前后沿第一族简单波特征线,Riemann不变量相等。
扰动前Riemann不变量=V0·n+
| ${\mathit{\boldsymbol{V}}_b} \cdot \mathit{\boldsymbol{n}} + \frac{{2{c_b}}}{{\gamma - 1}}{\text{ = }}\frac{{2{c_0}}}{{\gamma - 1}}$ | (10) |
式中:下标b对应扰动后流动量,下标0对应扰动前定常流的流动量,Vb·n为法向速度,n为单位物面外法向。由声速
| $\begin{gathered} \frac{{{p_b}}}{{{p_0}}} = {\left[ {1 - \frac{{\gamma - 1}}{2}\sqrt {\frac{{{\rho _0}}}{{\gamma {p_0}}}} {\mathit{\boldsymbol{V}}_b} \cdot \mathit{\boldsymbol{n}}} \right]^{\frac{{2\gamma }}{{\gamma - 1}}}} = \hfill \\ \;\;\;\;\;\;\;\;1 - \frac{{2\gamma }}{{\gamma - 1}}\frac{{\gamma - 1}}{2}\sqrt {\frac{{{\rho _0}}}{{\gamma {p_0}}}} {\mathit{\boldsymbol{V}}_b} \cdot \mathit{\boldsymbol{n}} + \cdots \hfill \\ \end{gathered} $ | (11) |
舍去高阶扰动量,式(11)可改写为
| ${p_b} = {p_0} - \sqrt {\gamma {\rho _0}{p_0}} {\mathit{\boldsymbol{V}}_b} \cdot \mathit{\boldsymbol{n}} = {p_0} - \sqrt {\gamma {\rho _0}{p_0}} {V_{bn}}$ | (12) |
式中法向速度Vbn由角速度扰动引起。可以看出,如果物面向着流体运动,则物面压强会提高;反之,背着流体运动,则物面压强会减小。沿用欧拉方程基本流所用的量纲一参考量,式(12)量纲一化后,形式是一致的。因此,利用式(12)可得压力系数为
| $C{p_b} = C{p_0} - \frac{2}{{\sqrt \gamma Ma_\infty ^2}}\sqrt {{{\bar \rho }_0}{{\bar p}_0}} {{\bar V}_{bn}}$ | (13) |
式中ρ0, p0, Vbn为量纲一量。这里Vbn指的是流体,对应于压力扰动,可理解为用来抵消角速度扰动引起的物面Vn,即Vbn+Vn=0,因此由式(9)可得
| $ {{\bar V}_{bn}} = - \sqrt \gamma M{a_\infty }\left[ {\left( {{{\bar \omega }_y}\frac{{\Delta z}}{{{l_y}}} - {{\bar \omega }_z}\frac{{\Delta y}}{{{l_z}}}} \right)} \right.\frac{{{s_x}}}{{{s_0}}} + \\ \;\;\;\;\;\;\;\;\left( {{{\bar \omega }_z}\frac{{\Delta x}}{{{l_z}}} - {{\bar \omega }_x}\frac{{\Delta z}}{{{l_x}}}} \right)\frac{{{s_y}}}{{{s_0}}} + \left. {\left( {{{\bar \omega }_x}\frac{{\Delta y}}{{{l_x}}} - {{\bar \omega }_y}\frac{{\Delta x}}{{{l_y}}}} \right)\frac{{{s_z}}}{{{s_0}}}} \right] $ | (14) |
式(13)在ω(0, 0, 0)点处Taylor级数展开,并舍去高阶项有
| $ C{p_b} = C{p_0} - \frac{2}{{\sqrt \gamma Ma_\infty ^2}}\sqrt {{{\bar \rho }_0}{{\bar p}_0}} {{\bar V}_{bn}} = C{p_0} + \frac{{\partial C{p_b}}}{{\partial {{\bar \omega }_x}}}{{\bar \omega }_x} + \\ \;\;\;\;\;\;\;\;\;\;\frac{{\partial C{p_b}}}{{\partial {{\bar \omega }_y}}}{{\bar \omega }_y} + \frac{{\partial C{p_b}}}{{\partial {{\bar \omega }_z}}}{{\bar \omega }_z} $ | (15) |
式中压力系数的偏微分(压力系数旋转导数)可写为
| $\frac{{\partial C{p_b}}}{{\partial {{\bar \omega }_i}}} = - \frac{2}{{\sqrt \gamma Ma_\infty ^2}}\sqrt {{{\bar \rho }_0}{{\bar p}_0}} \frac{{\partial {{\bar V}_{bn}}}}{{\partial {{\bar \omega }_i}}}\;\;\;\;\;\;i = x,y,z$ | (16) |
经数学处理后可以得到
| $\left\{ \begin{gathered} Cp_b^{{{\bar \omega }_x}} = \frac{{\partial C{p_b}}}{{\partial {{\bar \omega }_x}}} = \frac{{2\sqrt {{{\bar \rho }_0}{{\bar p}_0}} }}{{M{a_\infty }{l_x}{s_0}}}\left( { - \Delta z{s_y} + \Delta y{s_z}} \right) \hfill \\ Cp_b^{{{\bar \omega }_y}} = \frac{{\partial C{p_b}}}{{\partial {{\bar \omega }_y}}} = \frac{{2\sqrt {{{\bar \rho }_0}{{\bar p}_0}} }}{{M{a_\infty }{l_y}{s_0}}}\left( {\Delta z{s_x} - \Delta x{s_z}} \right) \hfill \\ Cp_b^{{{\bar \omega }_z}} = \frac{{\partial C{p_b}}}{{\partial {{\bar \omega }_z}}} = \frac{{2\sqrt {{{\bar \rho }_0}{{\bar p}_0}} }}{{M{a_\infty }{l_z}{s_0}}}\left( { - \Delta y{s_x} + \Delta x{s_y}} \right) \hfill \\ \end{gathered} \right.$ | (17) |
取物面微元ds=nds0,ds0为微元面积,n=(nx, ny, nz)为单位外法向量。角速度产生的物面微元气动力旋转导数共9个,即
| $\left\{ {\begin{array}{*{20}{c}} \begin{gathered} {\text{d}}C_x^{{{\bar \omega }_i}} = - Cp_b^{{{\bar \omega }_i}}{n_x}{\text{d}}{s_0} \hfill \\ {\text{d}}C_y^{{{\bar \omega }_i}} = - Cp_b^{{{\bar \omega }_i}}{n_y}{\text{d}}{s_0} \hfill \\ {\text{d}}C_z^{{{\bar \omega }_i}} = - Cp_b^{{{\bar \omega }_i}}{n_z}{\text{d}}{s_0} \hfill \\ \end{gathered} &{i = x,y,z} \end{array}} \right.$ | (18) |
角速度产生的物面微元气动力矩旋转导数也有9个, 即
| $\left\{ {\begin{array}{*{20}{c}} \begin{gathered} {\text{d}}C_{{m_x}}^{{{\bar \omega }_i}} = {\text{d}}C_z^{{{\bar \omega }_i}}\left( {y - {y_g}} \right) - {\text{d}}C_y^{{{\bar \omega }_i}}\left( {z - {z_g}} \right) \hfill \\ {\text{d}}C_{{m_y}}^{{{\bar \omega }_i}} = {\text{d}}C_x^{{{\bar \omega }_i}}\left( {z - {z_g}} \right) - {\text{d}}C_z^{{{\bar \omega }_i}}\left( {x - {x_g}} \right) \hfill \\ {\text{d}}C_{{m_z}}^{{{\bar \omega }_i}} = {\text{d}}C_y^{{{\bar \omega }_i}}\left( {x - {x_g}} \right) - {\text{d}}C_x^{{{\bar \omega }_i}}\left( {y - {y_g}} \right) \hfill \\ \end{gathered} &{i = x,y,z} \end{array}} \right.$ | (19) |
利用式(18,19)物面微元关系式,沿全弹表面积分可得到全弹气动力与气动力矩旋转导数
| $\left\{ {\begin{array}{*{20}{c}} \begin{gathered} C_j^{{{\bar \omega }_i}} = \frac{1}{{{S_r}}}\iint\limits_s {{\text{d}}C_j^{{{\bar \omega }_i}}} \hfill \\ C_{{m_j}}^{{{\bar \omega }_i}} = \frac{1}{{{S_r}{L_r}}}\iint\limits_s {{\text{d}}C_{{m_j}}^{{{\bar \omega }_i}}} \hfill \\ \end{gathered} &{i = x,y,z;\;j = x,y,z} \end{array}} \right.$ | (20) |
式中:Sr为参考面积,Lr为参考长度。Lr可参考量纲为一的角速度时的参考长度确定。
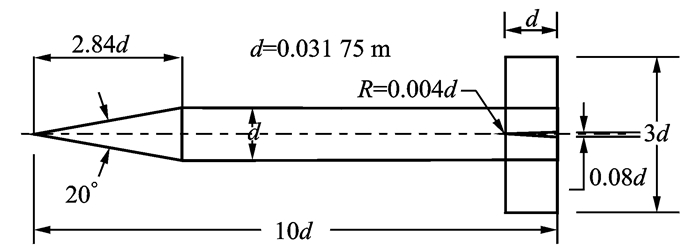
4 算例分析 4.1 计算模型Basic Finner导弹标模[6-7,11-12 ]是国际上验证旋转导数计算方法经常使用的模型。此导弹长细比为10,头部为锥形,弹体为圆柱形,十字形尾翼。弹径为d,尾翼厚度为0.08d,尾翼前缘倒圆半径为0.004d,具体尺寸见图 4。计算时质心位置在5.0d。
|
图 4 Basic Finner模型 Figure 4 Basic Finner model |
4.2 计算结果及分析
本文采用所提方法对上述计算模型在超声速范围内进行了多个马赫数的考核计算,个人PC机上Euler基本流场求解单点运行时间为40 min。
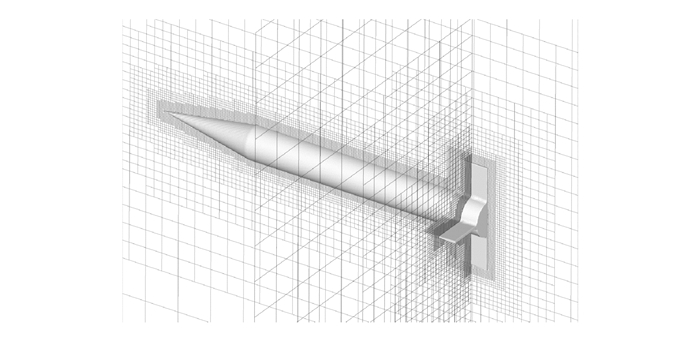
图 5是标模Basic Finner导弹采用笛卡尔网格生成的物面附近的网格,网格数为30万个。图 6是Ma= 2.03时Basic Finner导弹Euler方程解出的表面压力云图。
|
图 5 Basic Finner周围网格切面图 Figure 5 Meshes on cutting planes a round Basic Finner |

|
图 6 Ma=2.03的表面压力云图 Figure 6 Pressure contours on surface at Ma=2.03 |
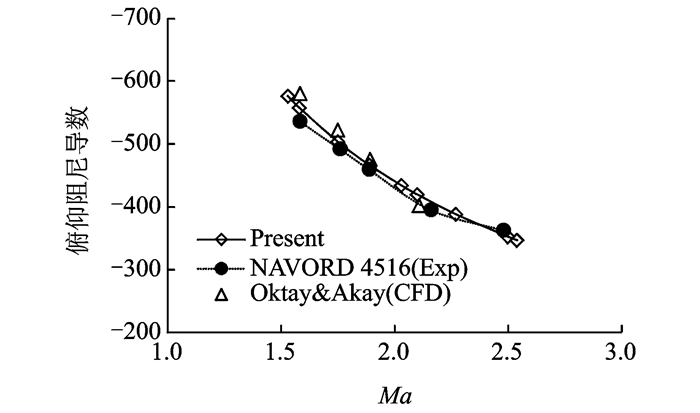
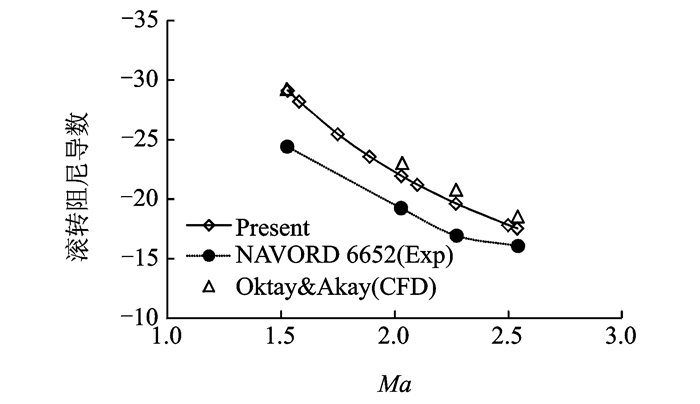
图 7,8分别是本文方法对Basic Finner导弹计算获得的俯仰阻尼导数和滚转阻尼导数,鉴于无弹翼洗流时差的影响,实际上就是旋转导数的考核结果[6, 11-12]。图中CFD是文献[6]通过求解强迫俯仰和滚转条件下的非定常Euler方程获得动导数。总体上,本文与试验和文献[6]的结果具有一致性。具体与试验比较,在测试的马赫数范围内,俯仰阻尼导数最大误差6.2%,滚转阻尼导数最大误差19.2%,均在试验数据25%的散布内,达到工程精度要求,说明本文方法具有工程适用性。
|
图 7 Basic Finner俯仰阻尼导数比较 Figure 7 Pitching moment d amping derivative comparison for Basic Finner |
|
图 8 Basic Finner滚转阻尼导数比较 Figure 8 Rolling moment damping derivative comparison for Basic Finner |
5 结束语
本文通过角速度引起的物面速度,基于非结构直角网格Euler方程基本流场解和对Riemann不变量摄动构建了超声速旋转导数快速计算方法。对国际旋转导数标模的计算考核,表明该方法具有相当好的精度。鉴于非结构直角网格Euler方程数值方法网格生成简单、省时、几何外形适用性强和流场解精度高的原因,本文方法可广泛应用于各种复杂气动外形的飞行器超声速旋转导数快速计算。
| [1] |
列别捷夫A A, 契尔诺勃洛夫金Л C. 无人驾驶飞行器的飞行动力学[M]. 张炳暄, 等译. 北京: 国防工业出版社, 1964.
|
| [2] |
BLAKE W B, SIMON J M. Tools for rapid analysis of aircraft and missile aerodynamics: AIAA-98-2793[R]. USA: AIAA, 1998. |
| [3] |
GREEN L L, SPENCE A M, MURPHY P C. Computational methods for dynamic stability and control derivatives: AIAA-2004-15[R]. USA: AIAA, 2004. |
| [4] |
叶川, 马东立.
利用CFD技术计算飞行器动导数[J]. 北京航空航天大学学报, 2013, 39(2): 196–219.
YE Chuan, MA Dongli. Aircraft dynamic derivatives calculation using CFD techniques[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 196–219. |
| [5] |
米百刚, 詹浩, 樊华羽.
飞行器组合及单独动导数数值求解方法研究[J]. 西北工业大学学报, 2015, 33(4): 540–545.
MI Baigang, ZHAN Hao, FAN Huayu. Calculating combined and single dynamic derivatives of flight vehicle calculation of dynamic derivatives for aircraft based on CFD technique[J]. Journal of Northwestern Polytenical University, 2015, 33(4): 540–545. |
| [6] |
OKTAY E, AKAY H U. CFD predictions of dynamic derivatives for missiles: AIAA-2002-0276[R]. USA: AIAA, 2002. |
| [7] |
孙智伟, 程泽荫, 白俊强, 等.
基于准定常的飞行器动导数的高效计算方法[J]. 飞行力学, 2010, 28(2): 28–30.
SUN Zhiwei, CHENG Zeyin, BAI Junqiang, et al. A high efficient method for computing dynamic derivatives of aircraft based on quasi-steady CFD method[J]. Flight Dynamics, 2010, 28(2): 28–30. |
| [8] |
THOMAS J P, DOWELL E H, Hall K C.
Modeling viscous transonic limit cycle oscillation behavior using a harmonic balance approach[J]. Journal of Aircraft, 2004, 41(6): 1266–1274.
DOI:10.2514/1.9839
|
| [9] |
MURMAN S M.
Reduced-frequency approach for calculating dynamic derivatives[J]. AIAA Journal, 2007, 45(6): 1161–1168.
DOI:10.2514/1.15758
|
| [10] |
黄明恪, 陈红全.
用非结构直角网格和欧拉方程计算运载火箭绕流[J]. 宇航学报, 2002, 23(5): 66–71.
HUANG Mingke, CHEN Hongquan. Computation of the flow past launch vehicle using unstructured Cartesian grid and Euler equations[J]. Journal of Astronautics, 2002, 23(5): 66–71. |
| [11] |
SHANTZ I, GROVES R T. Dynamic and static stability measurements of the basic finner at supersonic speeds: NAVORD Report 4516[R]. [S. l.]: [s. n.], 1960. |
| [12] |
REGAN F J. Roll damping moment measurements for the basic finner at subsonic and supersonic speeds: NAVORD Report 6652[R]. [S. l.]: [s. n.], 1964. |
| [13] |
FRINK N T, PARIKH P, PIRZADEH S. A fast upwind solver for the Euler equations on three-dimensional unstructured meshes: AIAA-91-0102[R]. [S. l.]: [s. n.], 1991. |
| [14] |
ROE P L.
Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43: 357–372.
DOI:10.1016/0021-9991(81)90128-5
|
 2018, Vol. 50
2018, Vol. 50


