电力系统作为重要的基础设施,稳定性一直是安全运行的基本要求,随着电力系统规模越来越大,如何保证电力系统安全、稳定和高效的运行一直是电力系统的研究重点和难点。电力系统属于复杂非线性系统,其突出特点表现在它的强非线性和结构工程的多变性[1]。电力系统稳定性[2]包括功角稳定、频率稳定和电压稳定。励磁控制器的优势在于[3]:系统稳定运行时,励磁电流时刻跟随负荷变化从而控制机端电压;通过控制励磁电流来控制无功功率以及功率角的变化;当系统受到扰动时,提高系统静态功率稳定和改善系统暂态稳定等。为解决这些稳定性问题,文献[4~5]指出,通过对励磁控制系统增加适当的控制,可以有效改善电力系统在干扰信号下的稳定性。文献[6]提出了两相无刷励磁机励磁电流的反馈控制、励磁频率和相序的速度参考控制,并通过仿真充分证明了其有效性。因此,如何设计高效励磁控制器成为了电力系统工作者研究的重点。
近年来,平方和理论发展迅速[7],文献[8]提出了一种保证系统全局非负定性的方案。多项式函数正定性的一个充分条件是可表示为平方和形式,而存在平方和分解等价于半定规划可行性问题。而SOSTOOL[8]正是解决这类问题的有力工具。平方和技术的发展,为多项式非线性系统控制器设计提供了新的思路。如文献[9]将贝尔曼等式松弛为不等式,通过求解平方和规划求出解。由于平方和方法的成功,其应用越来越广。在缺乏系统动态信息的情况下,文献[10]提出了一种基于平方和的全局半定规划方法,利用在线数据求解哈密顿-雅克比-伊萨克等式(Hamilton-Jacobi-Isaacs,HJI)。在平方和方法中,多项式系数是根据最小逼近误差原理确定的,这些系数在平方和可行凸集合中受到约束,从而保证了结果的非负定性。文献[11]将平方和方法用在分析多机电力系统稳定性上,并进一步优化,估计电力系统的吸引域。然而,文献[11]并没有将平方和方法应用到控制中。对于H∞最优控制问题,平方和方法应用很少,特别是在电力系统方面,因此,本文尝试将平方和方法应用于励磁控制器设计中。本文针对单机无穷大电力系统,通过泰勒方法,将非多项式系统转化为适用于平方和方法的多项式系统,同时保留了高阶无穷小项,并考虑系统建模时参数不确定性,重新定义干扰信号。由于平方和方法在构造Lyapunov函数、控制器参数优化等方面的优势,可以很好地将HJI等式问题松弛为不等式约束表示的最优问题,结合策略迭代方法,解决了长期以来求解HJI难的问题。最后通过仿真实验,验证了本文方法具有较强的鲁棒性和工程可实现性。
1 系统模型及问题描述随着控制理论的不断发展,电力系统励磁控制模型也不断变化[12-13]。电力系统的不确定性包括很多因素,如参数不确定性、外界干扰(故障)等。所以在设计过程中应充分考虑这些不确定因素,设计出具有鲁棒性的励磁控制系统。这样不仅能够有效地保证系统安全、高效和稳定运行,而且能够提高系统运行的经济效益。
1.1 单机无穷大电力系统模型考虑三阶单机无穷大电力系统模型,同时考虑各种因素带来的不确定性,以干扰信号的形式在模型中体现,则三阶无穷大电力系统模型用微分方程的形式表示为
| $ \begin{array}{l} \dot \delta = \omega \\ \dot \omega = \frac{{{\omega _0}}}{H}\left( {{P_m} - {P_e}} \right) - \frac{D}{H}\omega + {{\tilde d}_1}\\ {{\dot E'}_q} = - \frac{{{{E'}_q}}}{{{T_{d0}}}} + \frac{{{x_d} - {{x'}_d}}}{{{T_{d0}}{x_{ds}}}}{V_s}\cos \delta + \frac{{{E_f}}}{{{T_{d0}}}} + {{\tilde d}_2} \end{array} $ | (1) |
式中:Pe=E′qVssinδ/xds;
| $ \begin{array}{*{20}{c}} {{P_m} - \frac{{{{E'}_{q0}}{V_s}\sin {\delta _0}}}{{{{x'}_{ds}}}} = 0}\\ { - \frac{{{{E'}_{q0}}}}{{{T_{d0}}}} + \frac{{\left( {{x_d} - {{x'}_d}} \right){V_s}\cos {\delta _0}}}{{{T_{d0}}{{x'}_{ds}}}} + \frac{{{E_{f0}}}}{{{T_{d0}}}} = 0} \end{array} $ | (2) |
式中:δ0为稳态时的发电机转子运行角;E′q0为发电机稳态电势,由于后面小节所述平方和方法只适用于多项式系统,因此在这里通过泰勒公式展开为多项式。令x1=δ-δ0, x2=ω, x3=E′q-E′q0, u=Ef-Ef0,展开整理可得
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{{\dot x}_1} = {x_2}}\\ {{{\dot x}_2} = - \frac{{{\omega _0}}}{H}\left( {\frac{{{V_s}\sin {\delta _0}}}{{{x_{ds}}}}{x_3} + \frac{{{{E'}_{q0}}{V_s}}}{{{x_{ds}}}}{x_1}} \right) - \frac{D}{H}{x_2} + {d_1}\left( t \right)} \end{array}\\ {{\dot x}_3} = - \frac{1}{{{T_{d0}}}}{x_3} - \frac{{{x_d} - {{x'}_d}}}{{{T_{d0}}{x_{ds}}}}{V_s}\sin {\delta _0}{x_1} + {d_2}\left( t \right) \end{array} $ | (3) |
式中:d1=
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{k}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{d}} $ | (4) |
式中:
本文的目标是结合平方和方法以及策略迭代技术设计出H∞最优励磁控制器u,使其满足
| $ \int_0^T {\left( {{{\left\| {\mathit{\boldsymbol{z}}\left( t \right)} \right\|}^2} + {\mathit{\boldsymbol{u}}^2}\mathit{\boldsymbol{Ru}} - \gamma _0^2{{\left\| {\mathit{\boldsymbol{d}}\left( t \right)} \right\|}^2}} \right){\rm{d}}\left( t \right)} \le 0 $ | (5) |
式中:T≥0,
从H∞最优控制角度考虑,希望找到符合要求的γ0越小越好,其最小值记为γ*,以及对应的最优控制器记为u。理想的最优值γ*意味着电力系统的抗干扰能力更加强大:系统遭受到外界扰动(故障)时,在最优励磁控制器的调节作用下,能够更快速、更高效地收敛到工作点运行。文献[14]指出,对于给定的γ0,L2-增益问题可解的充分条件是存在光滑正定函数V使得下述HJI方程可解。
| $ \begin{array}{l} {\left( {\nabla V} \right)^{\rm{T}}}\mathit{\boldsymbol{f}} - \frac{1}{4}{\left( {\nabla V} \right)^{\rm{T}}}\mathit{\boldsymbol{g}}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{g}}^{\rm{T}}}\left( {\nabla V} \right) + \frac{1}{{4\gamma _0^2}}{\left( {\nabla V} \right)^{\rm{T}}}\\ \;\;\;\;\;\;\mathit{\boldsymbol{k}}{\mathit{\boldsymbol{k}}^{\rm{T}}}\nabla V + {\left\| \mathit{\boldsymbol{h}} \right\|^2} = 0,V\left( \mathit{\boldsymbol{0}} \right) = 0 \end{array} $ | (6) |
式中:相应的H∞励磁控制器u(x)=-(1/2)R-1gΤ(x)
步骤1 决策评估为
| $ \begin{array}{l} {\left( {\nabla {V_i}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{f}} + \mathit{\boldsymbol{g}}{\mathit{\boldsymbol{u}}_i}} \right) + \frac{1}{{4\gamma _0^2}}{\left( {\nabla {V_i}} \right)^{\rm{T}}}\mathit{\boldsymbol{k}}{\mathit{\boldsymbol{k}}^{\rm{T}}}\nabla {V_i} + \\ {\left\| \mathit{\boldsymbol{h}} \right\|^2} + \mathit{\boldsymbol{u}}_i^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{u}}_i} = 0,{V_i}\left( \mathit{\boldsymbol{0}} \right) = {\bf{0}} \end{array} $ | (7) |
步骤2 决策改进为
| $ {\mathit{\boldsymbol{u}}_{i + 1}}\left( \mathit{\boldsymbol{x}} \right) = - \frac{1}{2}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{g}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)\nabla {V_i}\left( \mathit{\boldsymbol{x}} \right) $ | (8) |
式中Vi为求解ui+1的候选李亚普诺夫函数。
然而,由于电力系统属于一类非线性非多项式系统,手工迭代计算量较大,造成V难以求解;其次,扰动抑制率γ0需要提前给定,而仅依靠经验选择γ0,不仅无法保证HJI等式可解,而且易产生较大的保守性,即在电力系统受到较大的故障扰动(如三相短路故障等)时,所设计的控制系统难以有效发挥作用,严重时甚至可能造成系统崩溃。
本文研究一类电力系统的H∞最优励磁控制设计问题,主要特点包括:(1)充分考虑了各种参数不确定性和外界扰动对系统的影响,且未限定扰动信号的具体形式(如上、下界等),具有一般性;(2)未对系统模型进行任何处理,保留了原系统的非线性特性;(3)采用基于平方和方法的策略迭代,将最小化扰动抑制率γ作为优化目标,降低了设计的保守性,每次迭代都是求解半定规划可行性问题的过程。
2 H∞最优控制方法将式(6)等效为
| $ \gamma _0^2{\left\| {\mathit{\boldsymbol{d}} - \frac{1}{{2\gamma _0^2}}{\mathit{\boldsymbol{k}}^{\rm{T}}}\nabla V} \right\|^2} - \mathit{\Gamma }\left( {V,\mathit{\boldsymbol{u}},{\gamma _0}} \right) = 0 $ | (9) |
式中:Γ(V, u, γ0)=-(
引理1[13] 对
| $ \begin{array}{*{20}{c}} {V\left( \mathit{\boldsymbol{x}} \right) \ge 0}\\ {\mathit{\Gamma }\left( {V,\mathit{\boldsymbol{u}},{\gamma _0}} \right) \ge 0} \end{array} $ |
则u(x)为H∞最优励磁控制器。
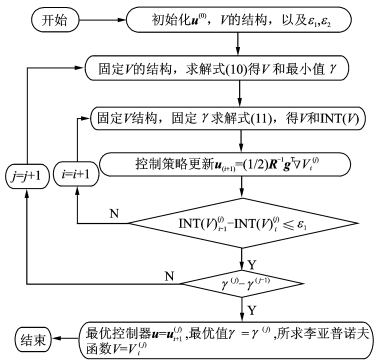
根据引理1,基于平方和方法和策略迭代技术,通过迭代求解多项式优化问题的方式,以最终获得H∞最优控制问题式(5)的解。如图 1所示,求解过程包括内外两层,其中外层循环使用上角标j表示,用来求解最优的扰动抑制率γ*,而内层循环使用下角标i来表示,用来求解李亚普诺夫函数V以及对应的最优励磁控制器u。
|
图 1 最优励磁控制设计流程图 Figure 1 Flow chart of optimal excitation control |
首先,初始化i=j=0,并利用文献[16]提供的方法对初始的V(0)结构(系数待定),u(0)以及γ0进行设定,其中V(0)为多项式平方和形式。然后,选择合适的且足够小的正常数ε1,ε2。值得注意的是:外循环中优化目标γ应为正数,且应求取最小值,而内循环首先会去求解出符合条件的V,进而将V对状态变量的积分作为目标函数,即∫ΩVdx,记作INT(V),并求取其最小值,其中Ω∈R3。最后将前后两次内循环中目标函数差的绝对值作为判断条件。
下面解释阐述该方法的具体步骤:
(1) 初始化满足假设1的u(0),正常数ε1, ε2和确定V的结构。
(2) 令j=0, 1, …, 并令u=u(0)求解下面的平方和程序
| $ \begin{array}{l} \mathop {\min }\limits_\gamma \gamma \\ \mathit{\Gamma }\left( {V,\mathit{\boldsymbol{u}},\gamma } \right)是平方和\\ V\;是平方和 \end{array} $ | (10) |
可以得到γ(j)以及V(j);
(3) 令i=1, 2, …, γi(j)=γ(j), Vi(j)=V(j),和ui(j)=u(j)。求解下面的平方和程序,解出符合条件的V
| $ \begin{array}{l} \mathop {\min }\limits_V \int_\mathit{\Omega } {V{\rm{d}}x} \\ \mathit{\Gamma }\left( {V,\mathit{\boldsymbol{u}}_i^{\left( j \right)},\gamma } \right)\\ V_{i - 1}^{\left( j \right)} - V\;是平方和\\ V\;是平方和 \end{array} $ | (11) |
可以得到Vi(j)以及目标函数对V的积分记作INT(V)i(j)。
(4) 控制决策更新
| $ {\mathit{\boldsymbol{u}}_{i + 1}} = - \frac{1}{2}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{g}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)\nabla V_i^{\left( j \right)}\left( \mathit{\boldsymbol{x}} \right) $ | (12) |
(5) 判断‖INT(V)i-1(j)-INT(V)i(j)‖≥ε1,如果成立,回到步骤(3),i=i+1;否则停止内循环,并令u=ui+1(j)和V=Vi(j)。
(6) 判断‖γ(j)-γ(j-1)‖≥ε2,如果成立,则回到步骤(2),j=j+1;若不成立则外循环,该方法结束,输出最优解γ, u以及V。
如果式(6)存在正定光滑解V0,在满足假设1的条件下,上述方法中式(10)存在非空解,励磁控制器ui+1是全局稳定控制器,同时,满足Γ(Vi, ui+1, γ0)≥Γ(Vi, ui, γ0),由Γ的定义,表明可寻找到更小γ′≤γ0,可以提高电力系统在受到扰动时能更好地保证同步的能力,弥补阻尼不足问题,避免出现振荡。目标函数γ保证了在每一次迭代过程中求解出逼近精确解V0。随着每次迭代,也更加接近精确解V0。同时,求解的极限值V∞(x)代替精确解V0。因而,通过松弛的策略迭代得到的u∞=-(1/2)R-1gT
使用第2小节介绍的方法,采用状态反馈的形式来设计H∞最优励磁控制器,使得当电力系统励磁控制模型(1)受到干扰时,能够快速地实现渐进稳定。首先对式(4)进行励磁控制器设计,并计算对应的李亚普诺夫函数以及扰动抑制率γ的最小值。本小节所用到的实验参数如表 1所示。
| 表 1 系统参数 Table 1 System parameters |
如第2小节所述,该设计方法包括内外循环,外循环负责求解扰动抑制率γ,判断条件应该选择尽量小,这样求解更为精确,抑制扰动的效果更加好,因此初始化判断条件ε1=10-4;而内循环目标函数为李亚普诺夫函数V对状态变量的积分,为了控制内循环的循环次数,与ε1相比可适当放大判定条件,在这里选择ε2=10-2;选择初始励磁控制器u(0)=-0.1x1+0.1x2-0.1x3。最后选择V为V=c1x12+c2x1x2+c3x22+c4x1x3+c5x2x3+c6x32, c1,…,c6为待定系数。
考虑到实际情况,当系统受到干扰时,发电机功角和暂态电动势应满足在稳定点附近工作,如果偏离太多,可能会造成整个系统的瘫痪,而相对转速的范围可适当选取较大的范围。因此,选择以下集合{x|-0.1 < x1 < 0.1, -2 < x2 < 2, -0.1 < x3 < 0.1}。同时,选择正定矩阵R=1。
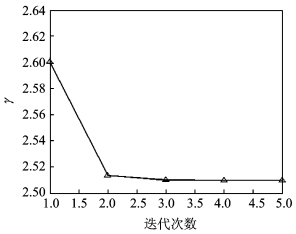
对式(4)应用提出的方法,经过5次迭代后,最优值γ为2.509 7,且γ的变化曲线为图 2。从图 2可以明显看出,γ收敛速度比较快,经过第3次迭代后,其变化幅度明显变小。这从实际证明了所述方法能够快速计算出最佳γ。
|
图 2 γ随迭代次数的变化情况 Figure 2 Changes of γ with number of iteration |
求解的Lyapunov函数V=37.71x12-0.012 06x1x2+0.623 2x1x3+2.401x22-1.968x2x3+0.407 6x32,与之对应的H∞励磁控制器u(5)=-0.085 37x1+0.269 6x2-0.111 7x3。
为了验证采用方法的有效性,测试求解的最优励磁控制器作用,将求解的励磁控制器u结合原系统,即式(1)进行2组实验对比。选择式(1)的稳定工作点为为(1.091, 0, 1.1),选择初始运行点(δ, ω, E′q)的值为(0.968 7, 0.5, 1.2)。
实验1 小干扰情况下系统仿真
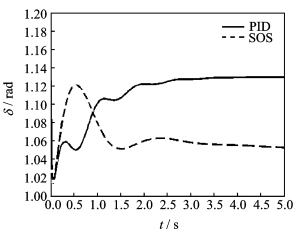
考虑系统存在干扰,包括外部干扰以及建模时的误差干扰,以正弦波的形式加入系统,选择干扰信号为d1=0.38(1-sin(8t))和d2=2/t-sint, 同时与经典的PID控制对比得到图 3和图 4的仿真结果。
|
图 3 小干扰情况下功角δ响应曲线 Figure 3 Response curves of work angle δ under small disturbance |

|
图 4 小干扰情况下相对转速ω响应曲线 Figure 4 Response curves of relative rotational speed ω under small disturbance |
从图 3可以明显看出,功角δ可以在2 s左右稳定到平衡点,与原平衡点相比,只有0.03 rad的差别,几乎可以忽略不计。与此同时,系统没有出现振荡等不良影响;而对比PID控制,虽然能够稳定系统,但是明显偏离原平衡点。而从图 4显示,相对转速ω能够在2.5 s左右就稳定到稳定工作点,与功角相比,相对转速没有跟踪误差,也没有产生任何振荡现象;而PID控制仿真结果明显产生了振荡幅值在0.006左右的振荡现象。通过对图 3和图 4的分析充分说明,对于小干扰信号,所采用的方法能够设计出有效励磁控制器u且使系统快速稳定到工作点。
实验2 大干扰情况下系统仿真
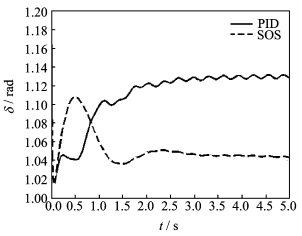
上面分析了在小干扰信号下系统的状态响应,为充分说明控制器的有效性,将干扰信号幅值放大20倍,其具体形式为d1=7.6(1-sin(8t))和d2=40/t-sint,得到图 5和图 6的仿真结果。
|
图 5 大干扰情况下功角δ响应曲线 Figure 5 Response curves of work angle δ under big disturbance |
|
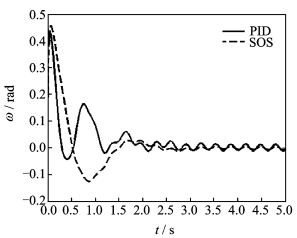
图 6 大干扰情况下相对转速ω响应曲线 Figure 6 Response curves of relative rotational speed ω under big disturbance |
从图 5可以明显看出,功角δ可以在2 s左右稳定到平衡点,这与在小干扰信号下其响应时间相同,然而由于干扰信号幅值太大,出现周期性小幅值振荡。而从图 6显示,相对转速ω能够在2.5 s左右就收敛到平衡点,与实验1相比,相对转速ω产生了周期性小幅值振荡。而观察PID控制实验结果,功角与相对转速都出现了明显的振荡现象,控制效果不佳。实验2说明,对于大干扰信号,H∞最优励磁控制器u同样能够有效抑制大干扰信号,且能快速使系统正常工作。
通过实验1和实验2, 证明了采用本文设计的励磁控制器能够有效抑制各种干扰信号,同时使得系统快速稳定到平衡点,使得系统能够安全、稳定工作。
4 结束语本文针对单机无穷大电力系统,提出了一种基于平方和方法的策略迭代H∞励磁控制器设计方法。为了使平方和方法适用于电力系统励磁控制器设计,利用泰勒展开将系统处理为多项式系统,并将高阶无穷小项加以考虑,重新定义干扰信号为d,提高了控制器对参数不确定性的鲁棒性。通过对系统的适当假设和处理后,本文方法使用内-外循环的迭代方式。在给定扰动抑制率γ的情况下,内层循环迭代通过求解HJI不等式得出Lyapunov函数以及对应的全局稳定励磁控制器;而外层循环迭代则可求解出最优扰动抑制率γ值,极大地提高了系统的抗干扰能力。最后的仿真实验表明,本文设计的励磁控制器可以在系统持续受到干扰信号的影响下,功角δ、相对转速ω快速稳定到工作点。由于设计过程中没有考虑干扰信号d的具体形式,因此本文方法对参数不确定性、建模误差和测量噪声在鲁棒性能上的提升效果明显。文中所述方法基于平方和理论,因此对于电力系统等非线性非多项式的应用提出了挑战;其次,繁重的计算负担也限制了平方和的应用。因此,平方和理论的发展成为克服这些问题的关键。
| [1] |
陈珩, 陈怡, 万秋兰, 等.
电力系统稳态分析[M]. 北京: 中国电力出版社, 2015.
CHEN Heng, CHEN Yi, WAN Qiulan, et al. Power system steady state analysis[M]. Beijing: China Electric Power Press, 2015. |
| [2] |
KUNDUR P, PASERBA J, AJJARAPU V, et al.
Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1387–1401.
DOI:10.1109/TPWRS.2004.825981
|
| [3] |
杨冠城.
电力系统自动装置原理[M]. 北京: 中国电力出版社, 2012: 44-49.
YANG Guancheng. Principle of power system automatic device[M]. Beijing: China Electric Power Press, 2012: 44-49. |
| [4] |
ZHAO Hongshan, LAN Xiaoming, ZHAO Junkai, et al.
Research on voltage nonlinear hierarchical prediction control of power system[J]. Proceedings of the Chinese Society for Electrical Engineering, 2016, 36(15): 4162–4171.
|
| [5] |
DING Jianshun, WANG Qing, XIANG Li, et al. Stability analysis of power system with under-excitation limiter in generator excitation control system[C]//International Conference on Intelligent Computation Technology and Automation. [S. l. ]: IEEE, 2016: 840-843. |
| [6] |
JIAO Ningfei, LIU Weiguo, MENG Tao, et al. Research on excitation control methods for the two-phase brushless exciter of wound-rotor synchronous starter/generators in the starting mode[C]//Applied Power Electronics Conference and Exposition. [S. l. ]: IEEE, 2016: 2776-2781. |
| [7] |
PARRILO P A. Structured semidefinite programs and semi-algebraic geometry methods in robustness and optimization[D]. California: California Institute of Technology, 2000. |
| [8] |
BLEKHERMAN G, PARRILO P A, THOMAS R R.
Semidefinite optimization and convex algebraic geometry[M]. [S.l.]: Society for Industrial and Applied Mathematics, 2012.
|
| [9] |
SUMMERS T H, KUNZ K, KARIOTOGLOU N, et al. Approximate dynamic programming via sum of squares programming[C]//Control Conference(ECC), 2013 European. [S. l. ]: IEEE, 2013: 191-197. |
| [10] |
JIANG Yu, JIANG Zhongping.
Global adaptive dynamic programming for continuous-time nonlinear systems[J]. IEEE Transactions on Automatic Control, 2015, 60(11): 2917–2929.
DOI:10.1109/TAC.2015.2414811
|
| [11] |
ANGHEL M, MILANO F, PAPACHRISTODOULOU A.
Algorithmic construction of Lyapunov functions for power system stability analysis[J]. IEEE Transactions on Circuits and Systems, 2013, 60(9): 2533–2546.
DOI:10.1109/TCSI.2013.2246233
|
| [12] |
卢强, 孙元章.
电力系统非线性控制[M]. 2版. 北京: 科学出版社, 2008.
LU Qiang, SUN Yuanzhang. Nonlinear control for electrical power system-second edition[M]. Beijing: Science Press, 2008. |
| [13] |
卢强, 梅生伟, 申铁龙, 等.
非线性H∞励磁控制器的逆推设计[J]. 中国科学[E辑], 2000, 30(1): 70–78.
LU Qiang, MEI Shengwei, SHEN Tielong, et al. Recursive design of nonlinear H∞ excitation controller[J]. Science in China[Series E], 2000, 30(1): 70–78. |
| [14] |
SCHAFT A, VAN Der J.
L2-gain analysis of nonlinear systems and nonlinear state-feedback control[J]. IEEE Transactions on Automatic Control, 2002, 37(6): 770–784.
|
| [15] |
ABU-KHALAF M, LEWIS F L, HUANG J.
Policy iterations on the Hlamilton-Jacobi-Isaacs equation for state feedback control with input saturation[J]. IEEE Transactions on Automatic Control, 2006, 51(12): 1989–1995.
DOI:10.1109/TAC.2006.884959
|
| [16] |
PRAJNA S, PAPACHRISTODOULOU A, WU F.
Nonlinear control synthesis by sum of squares optimization:A Lyapunov-based approach[J]. Proceedings of the Asian Control Conference, 2004, 5(1): 157–165.
|
 2018, Vol. 50
2018, Vol. 50


