随着人们在生产生活等方面需求的提高以及科技的迅速发展,控制系统规模越来越大,自动化技术在某些方面已经取代了人力。控制系统复杂度的不断提高使其发生故障的可能性也随之增大,产业一体化使得一旦某一个环节出现故障,轻则停车,重则造成严重的经济损失和人员伤亡。所以对系统进行故障诊断很有意义[1]。
大多数故障发生初期都是微小故障,故障特征不明显。随着系统运行,未被检测出来的微小故障会逐渐演变为对系统有较大危害的突变故障,产生严重后果。因此,微小故障的早期诊断很重要,及早发现及早治疗,降低危险程度。由于微小故障幅值小,变化缓慢,故障信息容易淹没在未知扰动和各类噪声、误差中,使得早期微小故障难以被及时发现[2]。因此, 国内外关于微小故障诊断的研究相对较少,多数还集中于特征比较明显的故障上[3-7]。
现有的微小故障诊断研究通常将原系统通过坐标变换解耦成两个子系统,其中一个子系统只有故障没有干扰,另外的子系统只有干扰没有故障,然后对其分别设计观测器,从而实现微小故障的早期诊断[2]。但在针对含干扰的子系统设计滑模观测器时,往往需要已知干扰的上界,如文献[8, 9]所述,这对干扰上界未知的情况是不适用的。针对干扰未知的系统进行故障诊断,文献[10, 11]给出一种基于未知输入观测器的诊断方法,但是只能用于诊断突变故障,微小故障会被淹没在干扰中。本文将原系统进行解耦,分成两个子系统,其中一个子系统只有故障没有干扰信号,因此便可以从该子系统入手进行微小故障的检测和估计。因此,本文提出了一种基于未知输入观测器的微小故障的早期诊断方法,既适用于干扰上界未知的系统,又可用于诊断微小故障,而且由于是针对解耦后只有干扰的子系统,使得设计未知输入观测器时减少了约束条件,更易求解。
传感器用于收集系统运行信息,不直接影响系统性能,因此对传感器的故障诊断研究相对较少。文献[8]提出了一种针对非线性系统传感器微小故障的诊断方法,将传感器故障转化成伪执行器故障,将执行器故障方法应用于传感器故障中。文献[10]提出一种传感器突变故障的检测方法,没有进行隔离或估计的研究。文献[12]提出一种自适应观测器估计牵引电机传感器故障,但没有考虑干扰的影响。文献[13]在干扰存在的情况下,设计滑模观测器对传感器微小故障进行了检测和隔离,没有进行故障估计研究。本文弥补了上述方法的不足,在考虑干扰的情况下,对传感器故障进行了估计。
故障诊断的研究成果有很多[12-21],文献[14]通过采用H∞性能指标,抑制干扰对故障诊断的影响,只是针对的是线性系统[3]。对于非线性系统,为了避免求解Lipschitz常数,本文采用小偏差线性化的方法对系统进行线性化,给出线性化的一般公式,只要找到稳态工作点,就可以直接利用线性化一般公式处理。这一方法在工程应用中比较常见,因为大多数系统实际工作在稳定状态。
综上所述,本文的创新点在于提供了微小故障诊断的一种方法,在现有的微小故障的解决方法中,通常是对解耦系统设计综合滑模-自适应或者滑模-龙伯格观测器,但都有个问题是,需要已知干扰信号幅值的上界,因此本文提出一种综合未知输入-自适应观测器的方法,该方法检测微小故障时不需要已知干扰信号幅值上界,且对于解耦后的含干扰的系统设计未知输入观测器时,减轻了观测器增益矩阵的求解约束,求解更加方便。其次,利用Lyapunov函数证明误差动态方程的稳定性并表示成线性矩阵不等式的形式,使得观测器增益矩阵的求解更简单。最后,仿真结果证明了所提方法的有效性。
1 问题描述 1.1 系统描述考虑如下形式的非线性动态系统
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{Ax}}\left( t \right) + {\mathit{\boldsymbol{f}}_a}\left( x \right) + \mathit{\boldsymbol{Bu}}\left( t \right) + \mathit{\boldsymbol{Ed}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{Cx}}\left( t \right) + \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{f}}_s}\left( t \right)} \end{array} $ | (1) |
式中:x∈Rn,u∈Rm,y∈Rp分别为系统的状态变量,输入变量和测量输出向量;fa(x)∈Rn是系统的非线性部分;d(t)∈Rr是系统的不确定部分(包括干扰,建模误差和参数变动等);fs(t)∈Rq是传感器微小故障,A∈Rn×n,B∈Rn×m,C∈Rp×n分别是系统矩阵,输入矩阵和输出矩阵;E∈Rn×r和F∈Rp×q是已知的适维矩阵。
假设1 rank(B)=m,rank(E)=r,rank(C[B E])=m+r,其中rank表示矩阵的秩。
假设2 (A, C)是可观的。
1.2 系统解耦因为微小故障本身的故障特征不明显,在未知干扰存在的情况下更是容易被淹没,为了能够及早诊断出微小故障,这里用坐标变换将原系统(1)解耦成两个子系统,其中一个子系统只含有故障,另一个子系统只含有干扰,下面给出一个引理。
引理 在假设1的保证下,存在坐标变换
| $ \mathit{\boldsymbol{z}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_1}}\\ {{\mathit{\boldsymbol{z}}_2}} \end{array}} \right] = \mathit{\boldsymbol{T}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}} \end{array}} \right],\mathit{\boldsymbol{\omega }} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\omega }}_1}}\\ {{\mathit{\boldsymbol{\omega }}_2}} \end{array}} \right] = \mathit{\boldsymbol{S}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_1}}\\ {{\mathit{\boldsymbol{y}}_2}} \end{array}} \right] $ | (2) |
使得原系统(1)被解耦成如下两个子系统:
子系统1
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot z}}}_1} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{z}}_1} + {\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{z}}_2} + {\mathit{\boldsymbol{f}}_{a1}}\left( {{\mathit{\boldsymbol{z}}_1},{\mathit{\boldsymbol{z}}_2}} \right) + {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{E}}_1}\mathit{\boldsymbol{d}}\\ {\mathit{\boldsymbol{\omega }}_1} = {\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{z}}_1} \end{array} \right. $ | (3) |
子系统2
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot z}}}_2} = {\mathit{\boldsymbol{A}}_3}{\mathit{\boldsymbol{z}}_1} + {\mathit{\boldsymbol{A}}_4}{\mathit{\boldsymbol{z}}_2} + {\mathit{\boldsymbol{f}}_{a2}}\left( {{\mathit{\boldsymbol{z}}_1},{\mathit{\boldsymbol{z}}_2}} \right) + {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{u}}\\ {\mathit{\boldsymbol{\omega }}_2} = {\mathit{\boldsymbol{C}}_4}{\mathit{\boldsymbol{z}}_2} + {\mathit{\boldsymbol{F}}_2}{\mathit{\boldsymbol{f}}_s} \end{array} \right. $ | (4) |
式中:z1∈Rr,ω1∈Rr,T∈Rn×n,S∈Rp×p,A1∈Rr×r,A4∈R(n-r)×(n-r),B1∈Rr×m,E1∈Rr×r,C1∈Rr×r,C4∈R(n-r)×(n-r),F2∈R(p-r)×q。
关于系统解耦方面在文献[8, 9]都有详细的介绍,本文就不再累述,这里只是证明原系统可以解耦成两个子系统,以便后面分别对其进行观测器的设计。
2 观测器设计 2.1 故障检测观测器的设计故障诊断的第一步是故障检测,即确定故障是否发生及故障发生的时刻。故障检测是故障诊断中最基本的一步,只有及时检测出故障才能及早采取措施补救。这一节首先给出针对未知扰动下的微小故障的故障检测观测器的设计方案。
在1.2节中,原系统已经被解耦成两个子系统,对于子系统(3),设计如下形式的未知输入观测器以消除未知扰动的影响
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot \upsilon }} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1}{{\mathit{\boldsymbol{\hat z}}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_2}{{\mathit{\boldsymbol{\hat z}}}_2} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{f}}_{a1}}\left( {{{\mathit{\boldsymbol{\hat z}}}_1},{{\mathit{\boldsymbol{\hat z}}}_2}} \right) + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{u}} + \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{K}}_1}\left( {{\mathit{\boldsymbol{\omega }}_1} - {{\mathit{\boldsymbol{\hat \omega }}}_1}} \right)\\ {{\mathit{\boldsymbol{\hat z}}}_1} = \mathit{\boldsymbol{\upsilon }} + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\omega }}_1}\\ {{\mathit{\boldsymbol{\hat \omega }}}_1} = {\mathit{\boldsymbol{C}}_1}{{\mathit{\boldsymbol{\hat z}}}_1} \end{array} \right. $ | (5) |
式中:“^”为相应变量的估计值;υ为观测器的状态变量;矩阵T,H,K1为待求矩阵。
对于子系统(4),设计简单的龙伯格观测器以检测传感器微小故障
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat z}}}_2} = {\mathit{\boldsymbol{A}}_3}{{\mathit{\boldsymbol{\hat z}}}_1} + {\mathit{\boldsymbol{A}}_4}{{\mathit{\boldsymbol{\hat z}}}_2} + {\mathit{\boldsymbol{f}}_{a2}}\left( {{{\mathit{\boldsymbol{\hat z}}}_1},{{\mathit{\boldsymbol{\hat z}}}_2}} \right) + {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{u + }}\\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{L}}_1}\left( {{\mathit{\boldsymbol{\omega }}_2} - {{\mathit{\boldsymbol{\hat \omega }}}_2}} \right)\\ {{\mathit{\boldsymbol{\hat \omega }}}_2} = {\mathit{\boldsymbol{C}}_4}{{\mathit{\boldsymbol{\hat z}}}_2} \end{array} \right. $ | (6) |
式中,L1是待求矩阵。
定义状态估计误差为e1=z1-
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot e}}}_1} = \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{z}}_1} - \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1}{{\mathit{\boldsymbol{\hat z}}}_1} + \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{z}}_2} - }\\ {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_2}{{\mathit{\boldsymbol{\hat z}}}_2} - \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{f}}_{a1}} - \mathit{\boldsymbol{T}}{{\mathit{\boldsymbol{\hat f}}}_{a1}} + \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{u}} - }\\ {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{e}}_1} + \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{E}}_1}\mathit{\boldsymbol{d}}} \end{array} $ | (7) |
| $ {{\mathit{\boldsymbol{\dot e}}}_2} = \left( {{\mathit{\boldsymbol{A}}_4} - {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{C}}_4}} \right){\mathit{\boldsymbol{e}}_2} + {\mathit{\boldsymbol{A}}_3}{\mathit{\boldsymbol{e}}_1} + {\mathit{\boldsymbol{f}}_{a2}} - {{\mathit{\boldsymbol{\hat f}}}_{a2}} $ | (8) |
式中,I表示单位矩阵。
从式(7,8)可以看出,如果令T=I-HC1, 则上式可以变成如下形式
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot e}}}_1} = \left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1} - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{e}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{e}}_2} + \mathit{\boldsymbol{T}}\left( {{\mathit{\boldsymbol{f}}_{a1}} - {{\mathit{\boldsymbol{\hat f}}}_{a1}}} \right) + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{E}}_1}\mathit{\boldsymbol{d}} \end{array} $ |
| $ {{\mathit{\boldsymbol{\dot e}}}_2} = \left( {{\mathit{\boldsymbol{A}}_4} - {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{C}}_4}} \right){\mathit{\boldsymbol{e}}_2} + {\mathit{\boldsymbol{A}}_3}{\mathit{\boldsymbol{e}}_1} + {\mathit{\boldsymbol{f}}_{a2}} - {{\mathit{\boldsymbol{\hat f}}}_{a2}} $ |
对于非线性部分的处理,多数文献应用的是Lipschitz条件,但是需要求解Lipschitz常数,本文利用小偏差线性化,给出线性化的一般公式,只要找到稳态工作点,就可以直接利用线性化一般公式处理。
假设稳态工作点是z0=[z10T z20T]T, 其中z10是子系统1的工作点,z20是子系统2的工作点,则有
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{a1}} = {\mathit{\boldsymbol{f}}_{a1}}\left( {{\mathit{\boldsymbol{z}}_0}} \right) + \frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_1} - {\mathit{\boldsymbol{z}}_{10}}} \right) + }\\ {\frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_2} - {\mathit{\boldsymbol{z}}_{20}}} \right)} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{a2}} = {\mathit{\boldsymbol{f}}_{a2}}\left( {{\mathit{\boldsymbol{z}}_0}} \right) + \frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_1} - {\mathit{\boldsymbol{z}}_{10}}} \right) + }\\ {\frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_2} - {\mathit{\boldsymbol{z}}_{20}}} \right)} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{a1}} = {\mathit{\boldsymbol{f}}_{a1}}\left( {{\mathit{\boldsymbol{z}}_0}} \right) + \frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_1} - {\mathit{\boldsymbol{z}}_{10}}} \right) + }\\ {\frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_2} - {\mathit{\boldsymbol{z}}_{20}}} \right)} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{a2}} = {\mathit{\boldsymbol{f}}_{a2}}\left( {{\mathit{\boldsymbol{z}}_0}} \right) + \frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_1} - {\mathit{\boldsymbol{z}}_{10}}} \right) + }\\ {\frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right.\left( {{\mathit{\boldsymbol{z}}_2} - {\mathit{\boldsymbol{z}}_{20}}} \right)} \end{array} $ |
为了书写的方便,记
| $ \frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = \frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = {\mathit{\boldsymbol{A}}_{11}} $ |
| $ \frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = \frac{{\partial {\mathit{\boldsymbol{f}}_{a1}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = {\mathit{\boldsymbol{A}}_{12}} $ |
| $ \frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = \frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_1}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = {\mathit{\boldsymbol{A}}_{21}} $ |
| $ \frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = \frac{{\partial {\mathit{\boldsymbol{f}}_{a2}}}}{{\partial {\mathit{\boldsymbol{z}}_2}}}\left| {_{\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_0}}} \right. = {\mathit{\boldsymbol{A}}_{22}} $ |
于是可以得到
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot e}}}_1} = \left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{11}} - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{e}}_1} + \mathit{\boldsymbol{T}}\left( {{\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{A}}_{12}}} \right){\mathit{\boldsymbol{e}}_2} + \\ \;\;\;\;\;\;\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{E}}_1}\mathit{\boldsymbol{d}} \end{array} $ |
| $ {{\mathit{\boldsymbol{\dot e}}}_2} = \left( {{\mathit{\boldsymbol{A}}_4} + {\mathit{\boldsymbol{A}}_{22}} - {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{C}}_4}} \right){\mathit{\boldsymbol{e}}_2} + \left( {{\mathit{\boldsymbol{A}}_3} + {\mathit{\boldsymbol{A}}_{21}}} \right){\mathit{\boldsymbol{e}}_1} $ |
从上式可以看出来,如果令TE1=0, 那么未知扰动对残差就没有影响,从而使得故障检测的鲁棒性得到满足,得到误差动态方程如下
| $ {{\mathit{\boldsymbol{\dot e}}}_1} = \left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{11}} - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{e}}_1} + \mathit{\boldsymbol{T}}\left( {{\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{A}}_{12}}} \right){\mathit{\boldsymbol{e}}_2} $ | (9) |
| $ {{\mathit{\boldsymbol{\dot e}}}_2} = \left( {{\mathit{\boldsymbol{A}}_4} + {\mathit{\boldsymbol{A}}_{22}} - {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{C}}_4}} \right){\mathit{\boldsymbol{e}}_2} + \left( {{\mathit{\boldsymbol{A}}_3} + {\mathit{\boldsymbol{A}}_{21}}} \right){\mathit{\boldsymbol{e}}_1} $ | (10) |
注1 本文考虑的未知扰动并不仅限于上界已知的情况,一定程度上解决了扰动完全未知的微小故障故障检测问题。
注2 在文献[11]中,T要满足TEd=0,TEf≠0。在本文中,因为解耦系统使干扰和故障分别存在于两个子系统中,所以T要满足的约束条件减少,理论上只要使得TE1=0即可,这样就解决了故障分布矩阵Ef和干扰分布矩阵Ed相等的问题,只要矩阵E1是非奇异矩阵,便可以找到观测器增益矩阵T。
注3 有的非线性系统的非线性部分并不满足Lipschitz条件,因此并不能用全局Lipschitz条件来处理。文献[22]给出了一个局部Lipschitz条件的处理方法,即已知系统工作的稳定点,假定其余状态均不超过此点,事实上,这种方法在某种程度为小偏差线性化提供了理论依据,而且工程中也常用此方法处理,有实际依据。
为了证明设计的观测器的稳定性,下面给出一个定理。
定理1 在没有发生传感器微小故障的情况下,如果存在对称正定矩阵P1,P2和矩阵Y1,Y2使得式(11)成立,则误差动态方程(9)和(10)是渐进稳定的。
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{11}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{12}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{12}^{\rm{T}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{13}}} \end{array}} \right] < 0 $ | (11) |
式中
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{11}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1} + {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} - \mathit{\boldsymbol{C}}_1^{\rm{T}}\mathit{\boldsymbol{Y}}_1^{\rm{T}} - {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{C}}_1} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{12}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3^{\rm{T}}{\mathit{\boldsymbol{P}}_2} + {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{11}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_4^{\rm{T}}{\mathit{\boldsymbol{P}}_2} + {\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_4} - \mathit{\boldsymbol{C}}_4^{\rm{T}}\mathit{\boldsymbol{Y}}_2^{\rm{T}} - {\mathit{\boldsymbol{Y}}_2}{\mathit{\boldsymbol{C}}_4} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{11}} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{2}} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{12}} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3} = {\mathit{\boldsymbol{A}}_3} + {\mathit{\boldsymbol{A}}_{21}} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_4} = {\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{A}}_{22}} $ |
并且矩阵T满足条件TE1=0。因此,待求矩阵K1=P1-1Y1,L1=P2-1Y2。
证明 取Lyapunov函数为V=V1+V2, 其中V1=e1TP1e1,V2=e2TP2e2,则根据误差动态方程(9)和(10)可以得到
| $ \begin{array}{l} {{\dot V}_1} = \mathit{\boldsymbol{e}}_1^{\rm{T}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1} + {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} - \mathit{\boldsymbol{C}}_1^{\rm{T}}\mathit{\boldsymbol{Y}}_1^{\rm{T}} - {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{e}}_1} + \\ \;\;\;\;\;2\mathit{\boldsymbol{e}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2}{\mathit{\boldsymbol{e}}_2} \end{array} $ |
| $ \begin{array}{l} {{\dot V}_2} = \mathit{\boldsymbol{e}}_2^{\rm{T}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_4^{\rm{T}}{\mathit{\boldsymbol{P}}_2} + {\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} - \mathit{\boldsymbol{C}}_1^{\rm{T}}\mathit{\boldsymbol{Y}}_1^{\rm{T}} - {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{e}}_2} + \\ \;\;\;\;\;2\mathit{\boldsymbol{e}}_1^{\rm{T}}\mathit{\boldsymbol{P}}2{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2}{\mathit{\boldsymbol{e}}_2} \end{array} $ |
令Y1=P1K1,Y2=P2L1, 则
| $ V = {{\dot V}_1} + {{\dot V}_2} = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varXi} e}} $ |
其中,e=[e1T e2T], 矩阵Ξ=
| $ \dot V = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varXi} e = }} - {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{\theta e}} \le - {\lambda _{\min }}\left( \mathit{\boldsymbol{\theta }} \right){\left\| \mathit{\boldsymbol{e}} \right\|^2} = - \mathit{\boldsymbol{\omega }}\left( t \right) $ | (12) |
其中λmin(Θ)表示矩阵Θ的最小特征值。
对式(12)进行积分,得到如下
| $ V\left( 0 \right) - V\left( t \right) \ge \int_0^T {\omega \left( \tau \right){\rm{d}}\tau } $ | (13) |
因为ω(t)>0,所以对于t≥0,0 <
| $ \mathop {\lim }\limits_{t \to \infty } \mathit{\boldsymbol{\omega }}\left( t \right) = {\lambda _{\min }}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)\mathop {\lim }\limits_{t \to \infty } {\left\| \mathit{\boldsymbol{e}} \right\|^2} = 0 $ | (14) |
也就是说
如果系统在时刻T发生传感器微小故障,这时的误差动态方程具有如下形式
| $ {{\mathit{\boldsymbol{\dot e}}}_1} = \left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{11}} - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{e}}_1} + \mathit{\boldsymbol{T}}\left( {{\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{A}}_{12}}} \right){\mathit{\boldsymbol{e}}_2} $ | (15) |
| $ {{\mathit{\boldsymbol{\dot e}}}_2} = \left( {{\mathit{\boldsymbol{A}}_4} + {\mathit{\boldsymbol{A}}_{22}} - {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{C}}_4}} \right){\mathit{\boldsymbol{e}}_2} + \left( {{\mathit{\boldsymbol{A}}_3} + {\mathit{\boldsymbol{A}}_{21}}} \right){\mathit{\boldsymbol{e}}_1} - {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{F}}_2}{\mathit{\boldsymbol{f}}_s} $ | (16) |
可见fs对e2有直接影响,为此,定义残差为r(t)=e2(t)=ω2(t)-
故障检测方案:系统在健康的情况下残差r(t)的幅值会在给定的阈值内,如果残差r(t)的幅值在时刻T超出了阈值,那么就判断系统在T时刻发生了传感器微小故障。
故障检测是故障诊断的第一步,在有些情况下需要故障的信息来进行容错控制,这时就需要故障的幅值等信息,下面就给出微小传感器故障估计的观测器设计方法。
2.2 自适应未知输入观测器的设计在解耦系统的基础上,对两个子系统分别设计观测器,对于含有未知扰动的子系统,依然是设计未知输入观测器来消除扰动的影响;对于含有传感器微小故障的系统,设计自适应观测器。
对于子系统(3),设计如下形式的未知输入观测器
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot \upsilon }} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1}{{\mathit{\boldsymbol{\hat z}}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_2}{{\mathit{\boldsymbol{\hat z}}}_2} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{f}}_{a1}}\left( {{{\mathit{\boldsymbol{\hat z}}}_1},{{\mathit{\boldsymbol{\hat z}}}_2}} \right) + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{u}} + \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{K}}_2}\left( {{\mathit{\boldsymbol{\omega }}_1} - {{\mathit{\boldsymbol{\hat \omega }}}_1}} \right)\\ {{\mathit{\boldsymbol{\hat z}}}_1} = \mathit{\boldsymbol{\upsilon }} + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\omega }}_1}\\ {{\mathit{\boldsymbol{\hat \omega }}}_1} = {\mathit{\boldsymbol{C}}_1}{{\mathit{\boldsymbol{\hat z}}}_1} \end{array} \right. $ | (17) |
式中矩阵T,H,K2是待求矩阵。
对于子系统(4),设计如下自适应观测器
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat z}}}_2} = {\mathit{\boldsymbol{A}}_3}{{\mathit{\boldsymbol{\hat z}}}_1} + {\mathit{\boldsymbol{A}}_4}{{\mathit{\boldsymbol{\hat z}}}_2} + {\mathit{\boldsymbol{f}}_{a2}}\left( {{{\mathit{\boldsymbol{\hat z}}}_1},{{\mathit{\boldsymbol{\hat z}}}_2}} \right) + {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{u + }}\\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{L}}_2}\left( {{\mathit{\boldsymbol{\omega }}_2} - {{\mathit{\boldsymbol{\hat \omega }}}_2}} \right)\\ {{\mathit{\boldsymbol{\hat \omega }}}_2} = {\mathit{\boldsymbol{C}}_4}{{\mathit{\boldsymbol{\hat z}}}_2} + {\mathit{\boldsymbol{F}}_2}{{\mathit{\boldsymbol{\hat f}}}_s} \end{array} \right. $ | (18) |
式中:L2为待求矩阵;
定义状态估计误差为e1=z1-
| $ {{\mathit{\boldsymbol{\dot e}}}_1} = \left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{11}} - {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{C}}_1}} \right){\mathit{\boldsymbol{e}}_1} + \mathit{\boldsymbol{T}}\left( {{\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{A}}_{12}}} \right){\mathit{\boldsymbol{e}}_2} $ | (19) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot e}}}_2} = \left( {{\mathit{\boldsymbol{A}}_4} + {\mathit{\boldsymbol{A}}_{22}} - {\mathit{\boldsymbol{L}}_2}{\mathit{\boldsymbol{C}}_4}} \right){\mathit{\boldsymbol{e}}_2} + \left( {{\mathit{\boldsymbol{A}}_3} + {\mathit{\boldsymbol{A}}_{21}}} \right){\mathit{\boldsymbol{e}}_1} - \\ \;\;\;\;\;\;{\mathit{\boldsymbol{L}}_2}{\mathit{\boldsymbol{F}}_2}{\mathit{\boldsymbol{e}}_f} \end{array} $ | (20) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot e}}}_f} = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{e}}_2} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{M}}_2}\left( {{\mathit{\boldsymbol{A}}_4} + {\mathit{\boldsymbol{A}}_{22}} - {\mathit{\boldsymbol{L}}_2}{\mathit{\boldsymbol{C}}_4}} \right){\mathit{\boldsymbol{e}}_2} + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{M}}_2}\left( {{\mathit{\boldsymbol{A}}_3} + {\mathit{\boldsymbol{A}}_{21}}} \right){\mathit{\boldsymbol{e}}_1} - \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{L}}_2}{\mathit{\boldsymbol{F}}_2}{\mathit{\boldsymbol{e}}_f} \end{array} $ | (21) |
下面给出另外一个定理来证明所提自适应未知输入观测器的稳定性。
定理2 如果存在对称正定矩阵P1,P2和矩阵Y1,Y2使得式(22)成立,则误差动态方程(19), (20)和(21)是渐进稳定的
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{21}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{22}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{23}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{22}^{\rm{T}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{24}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{25}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{23}^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{25}^{\rm{T}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{26}}} \end{array}} \right] < 0 $ | (22) |
式中,
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{21}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1} + {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} - \mathit{\boldsymbol{C}}_1^{\rm{T}}\mathit{\boldsymbol{Y}}_1^{\rm{T}} - {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{C}}_1} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{24}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_4^{\rm{T}}{\mathit{\boldsymbol{P}}_2} + {\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_4} - \mathit{\boldsymbol{C}}_4^{\rm{T}}\mathit{\boldsymbol{Y}}_2^{\rm{T}} - {\mathit{\boldsymbol{Y}}_2}{\mathit{\boldsymbol{C}}_4} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{26}} = - \mathit{\boldsymbol{F}}_2^{\rm{T}}\mathit{\boldsymbol{Y}}_2^{\rm{T}} - {\mathit{\boldsymbol{Y}}_2}{\mathit{\boldsymbol{F}}_2} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{22}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3^{\rm{T}}{\mathit{\boldsymbol{P}}_2} + {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2} $ |
| $ \begin{array}{l} \\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{23}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3^{\rm{T}}{\mathit{\boldsymbol{P}}_2} \end{array} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{25}} = \mathit{\boldsymbol{0}} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_1} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{11}} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_2} + \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}_{12}} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3} = {\mathit{\boldsymbol{A}}_3} + {\mathit{\boldsymbol{A}}_{21}} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_4} = {\mathit{\boldsymbol{A}}_4} + {\mathit{\boldsymbol{A}}_{22}} $ |
并且矩阵T满足条件Te1=0。因此,待求矩阵K2=P1-1Y1,L2=P2-1Y2,其中,故障的自适应律
证明 这里的证明与定理1的证明类似,故此省略。
注4 同样,此自适应未知输入观测器适应于未知扰动上界是未知的情况,关于本文中解耦系统下的未知输入观测器的优势与2.1节故障检测部分相同,这里就不叙述了。
注5 在文献[9]中,按照自适应律,故障估计值为e1和e2的纯积分项,而本文中故障估计值为
| $ \mathit{\boldsymbol{\hat f = - \boldsymbol{\varGamma} }}\left( {{\mathit{\boldsymbol{M}}_1}\int_T^t {{e_2}\left( \tau \right){\rm{d}}\tau {\rm{ + }}{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{e}}_2}} } \right) $ |
增加的比例项提高了故障估计的性能,且考虑到传感器微小故障对e2的直接作用,因此,故障自适应律选择e2的比例项和积分项,使得故障估计更加迅速。
注6 基于自适应未知输入观测器进行故障估计的前提是
注7 相比于文献[9],本文所提自适应未知输入观测器的稳定性的证明以线性矩阵不等式(Linear matrix inequalities, LMI)的形式给出,因此,观测器增益矩阵更易求解。另外,可以通过LMI区域优化观测器增益矩阵,使极点配置到相应LMI区域。
为了证明未知扰动下的微小故障检测观测器和自适应未知输入观测器的有效性,下面给出一个电机实例。
3 试验 3.1 系统介绍牵引电机与其他电机建模原理相同,根据其电压方程,磁链方程,转矩方程和运动方程,得到理想情况d-q坐标下的牵引电机数学模型如下
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{Ax}}\left( t \right) + {\mathit{\boldsymbol{F}}_a}\left( x \right) + \mathit{\boldsymbol{Bu}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{Cx}}\left( t \right)} \end{array} $ |
式中:x(t)=[x1 x2 x3 x4 x5]T=[isq isd λrq λrd ωm]T,u(t)=[usq usd]T,
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_a}\left( {x\left( t \right)} \right) = \left[ {\begin{array}{*{20}{c}} { - {n_{\rm{p}}}\beta {x_5}{x_4}}\\ {{n_{\rm{p}}}\beta {x_5}{x_3}}\\ {{n_{\rm{p}}}\beta {x_5}{x_4}}\\ { - {n_{\rm{p}}}\beta {x_5}{x_3}}\\ {\mu \left( {{x_4}{x_1} - {x_3}{x_2}} \right)} \end{array}} \right],\mathit{\boldsymbol{A}} = \\ \left[ {\begin{array}{*{20}{c}} { - \gamma }&{ - {\omega _{\rm{s}}}}&{\alpha \beta }&0&0\\ {{\omega _{\rm{s}}}}&{ - \gamma }&0&{\alpha \beta }&0\\ {\alpha {L_m}}&0&{ - \alpha }&{ - {\omega _{\rm{s}}}}&0\\ 0&{\alpha {L_m}}&{{\omega _{\rm{s}}}}&{ - \alpha }&0\\ 0&0&0&0&0 \end{array}} \right], \end{array} $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{\delta {L_{\rm{s}}}}}}&0\\ 0&{\frac{1}{{\delta {L_{\rm{s}}}}}}\\ 0&0\\ 0&0\\ 0&0 \end{array}} \right],\;\;\;\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&1&0&0&0\\ 0&0&0&0&1 \end{array}} \right]. $ |
式中,
本文电机参数可以查阅文献[14]。通常来说,温度会改变电阻阻值,因此,在电机运行的过程中,由于温度变化或其他原因会导致电机转子阻值这一参数发生变化,在这里,把这一参数变化作为干扰信号,同时考虑速度传感器微小故障,得到如下电机模型
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{Ax}}\left( t \right) + {\mathit{\boldsymbol{F}}_a}\left( {\mathit{\boldsymbol{x}}\left( t \right)} \right) + \mathit{\boldsymbol{Bu}}\left( t \right) + \mathit{\boldsymbol{Ed}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{Cx}}\left( t \right) + \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}_{s\omega }}\left( t \right)} \end{array} $ | (23) |
式中,
| $ \mathit{\boldsymbol{F}}{\rm{ = [0}}\;\;{\rm{0}}\;\;{\rm{0}}\;\;{\rm{0}}\;\;{\rm{2}}{{\rm{]}}^{\rm{T}}} $ |
在进行速度传感器微小故障早期诊断之前,需要将系统(23)进行解耦处理。从系统(23)可以看出,只需令T=I5,S=I5, 可以得到如下两个解耦子系统
子系统1
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot z}}}_1} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{z}}_1} + {\mathit{\boldsymbol{F}}_{a1}}\left( {{\mathit{\boldsymbol{z}}_1},{\mathit{\boldsymbol{z}}_2}} \right) + {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{e}}_1}\mathit{\boldsymbol{d}}\\ {\mathit{\boldsymbol{\omega }}_1} = {\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{z}}_1} \end{array} \right. $ |
子系统2
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot z}}}_2} = {\mathit{\boldsymbol{A}}_4}{\mathit{\boldsymbol{z}}_2} + {\mathit{\boldsymbol{F}}_{a2}}\left( {{\mathit{\boldsymbol{z}}_1},{\mathit{\boldsymbol{z}}_2}} \right) + {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{u}}\\ {\omega _2} = {\mathit{\boldsymbol{C}}_4}{\mathit{\boldsymbol{z}}_2} + {\mathit{\boldsymbol{F}}_2}{\mathit{\boldsymbol{F}}_{s\omega }} \end{array} \right. $ |
式中,A1=A(1:4, 1:4)(其中,(1:4,1:4)表示取矩阵A中的第1~4行,第1~4列的4×4的方阵,下同),A4=0,e1=E(1:4, 1:4),Fa1=Fa(1:4),Fa2=Fa(5),B1=B(1:4),B2=0,C1= C(1:2, 1:4),C2=1,F2=2,并且根据Te1=0和T=I-HC1,可以得到
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0\\ 0&0&0&0\\ {\frac{1}{\beta }}&0&1&0\\ 0&{\frac{1}{\beta }}&0&1 \end{array}} \right],\;\;\;\;\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1\\ { - \frac{1}{\beta }}&0\\ 0&{ - \frac{1}{\beta }} \end{array}} \right] $ |
在仿真时,给出两种形式的故障,一种是渐变微小故障,用于描述速度传感器故障缓慢发生;另一种是常值微小故障,用于描述速度传感器故障突然发生且幅值较小的情况,用数学表达式可以表示成如下形式:
情况a 在第1 s时发生渐变微小故障
| $ {F_{s\omega }}\left( t \right) = \left\{ {\begin{array}{*{20}{c}} 0&{0 \le t < 1}\\ {1 - {{\rm{e}}^{ - 0.8\left( {t - 1} \right)}}}&{t \ge 1} \end{array}} \right. $ |
情况b 在第1 s时发生常值微小故障
| $ {F_{s\omega }}\left( t \right) = \left\{ {\begin{array}{*{20}{c}} 0&{0 \le t < 1}\\ 1&{t \ge 1} \end{array}} \right. $ |
下面给出两种情况下的故障检测仿真和故障估计仿真结果。
(1) 故障检测结果
从图 1,2可以看出,2.1节的故障检测方案是有效的,当故障发生时,残差超过阈值从而报警,检测出故障。作为对比,下面给出文献[11]中未知输入观测器对于故障情况A和B的检测结果。
|
图 1 情况A下的残差 Figure 1 Residual in Case A |
|
图 2 情况B下的残差 Figure 2 Residual in Case B |
从图 3, 4可以看出,文献[11]中的基于未知输入观测器的故障检测方法不能检测出传感器微小故障,对于渐变微小故障更是不敏感,而本文2.2节所提解耦系统下的基于未知输入观测器的故障检测方法是有效的。
(2) 故障估计结果
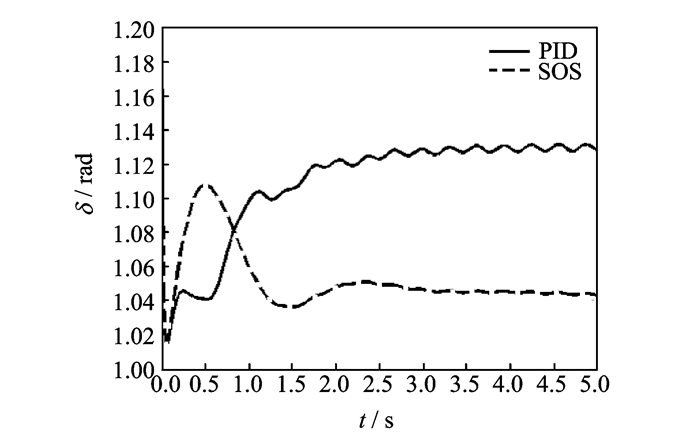
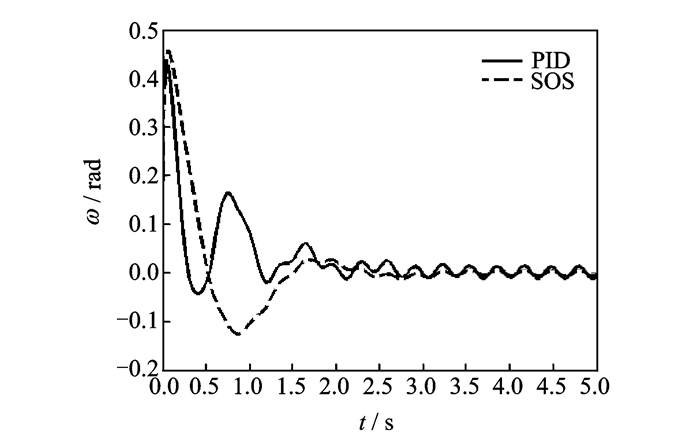
从图 5, 6可以看出,故障幅值为1 rad/s,故障量级约为0.4%,在幅值上可以看作是微小故障,且故障估计值约为0.996和0.997 rad/s,故障估计的准确率大于99.6%,应该是可以接受的,因此,定理2提出的自适应未知输入观测器实现了对速度传感器微小故障的估计。
|
图 5 情况A下的故障及其估计值 Figure 5 Fault and its estimation in Case A |
|
图 6 情况B下的故障及其估计值 Figure 6 Fault and its estimation in Case B |
4 结束语
本文提出一种传感器微小故障的诊断方法,并将其应用于电机系统。为了及时诊断出微小故障,引入坐标变换将原系统解耦成两个子系统,针对子系统各自的特性分别设计相应的观测器进行检测和估计,尤其解耦系统下的未知输入观测器解决了未知扰动上界下的故障诊断,同时减少了设计观测器的约束条件,最后的仿真结果证明了所提方法的有效性。如何提高微小故障估计的性能将是下一步的研究重点。
| [1] |
姜斌, 赵静, 齐瑞云, 等.
近空间飞行器故障诊断与容错控制的研究进展[J]. 南京航空航天大学学报, 2012, 44(5): 603–610.
JIANG Bin, ZHAO Jing, QI Ruiyun, et al. Research of fault diagnosis and fault tolerant control for near space vehicle[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2012, 44(5): 603–610. |
| [2] |
李娟, 周东华, 司小胜.
微小故障诊断方法综述[J]. 控制理论与应用, 2012, 29(12): 1517–1529.
LI Juan, ZHOU Donghua, SI Xiaosheng. Review of incipient fault diagnosis methods[J]. Control Theory and Application, 2012, 29(12): 1517–1529. |
| [3] |
JIANG B, CHOWDHURY F N.
Fault estimation and accommodation for linear MIMO discrete-time systems[J]. IEEE Transactions on Control Systems Technology, 2005, 13(3): 493–499.
DOI:10.1109/TCST.2004.839569
|
| [4] |
MONDAL S, CHAKRABORTY G, BHATTACHARYYA K.
Robust unknown input observer for nonlinear systems and its application to fault detection and isolation[J]. Journal of Dynamic Systems Measurement and Control, 2008, 130(4): 472–480.
|
| [5] |
LI H, GAO Y, SHI P, et al.
Observer-based fault detection for nonlinear systems with sensor fault and limited communication capacity[J]. IEEE Transactions on Automatic Control, 2016, 61(9): 2745–2751.
DOI:10.1109/TAC.2015.2503566
|
| [6] |
EMAMI K, FERNANDO T, NENER B, et al.
A functional observer based fault detection technique for dynamical systems[J]. Journal of the Franklin Institute, 2015, 352(5): 2113–2128.
DOI:10.1016/j.jfranklin.2015.02.006
|
| [7] |
JIANG B, CHOWDHURY F N.
Parameter fault detection and estimation of a class of nonlinear systems using observers[J]. Journal of the Franklin Institute, 2005, 342(7): 725–736.
DOI:10.1016/j.jfranklin.2005.04.007
|
| [8] |
ZHANG J, SWAIN A K, NGUANG S K.
Detection and isolation of incipient sensor faults for a class of uncertain non-linear systems[J]. IET Control Theory & Applications, 2012, 6(12): 1870–1880.
|
| [9] |
柳春, 姜斌, 张柯, 等.
带扰动的线性系统微小故障早期诊断方法[J]. 上海交通大学学报, 2015, 49(6): 889–896.
LIU Chun, JIANG Bin, ZHANG Ke, et al. An early fault diagnosis method for linear system with disturbance[J]. Journal of Shanghai Jiao Tong University, 2015, 49(6): 889–896. |
| [10] |
ZHANG C F, HUANG Y S, SHAO R.
Robust sensor faults detection for induction motor using observer[J]. Journal of Control Theory and Applications, 2012, 10(4): 528–532.
DOI:10.1007/s11768-012-0193-9
|
| [11] |
张昌凡, 黄宜山, 邵瑞.
基于观测器的感应电机故障检测方法及应用[J]. 仪器仪表学报, 2011, 32(6): 1337–1343.
ZHANG Changfan, HUANG Yishan, SHAO Rui. The fault detection method and application based on observers for induction motors[J]. Journal of Instrumentation, 2011, 32(6): 1337–1343. |
| [12] |
王占山, 张化光.
故障估计的自适应观测器设计[J]. 东北大学学报(自然科学版), 2005, 26(1): 221–224.
WANG Zhanshan, ZHANG Huaguang. An adaptive observer for fault estimation[J]. Journal of Northeastern University (Natural Science Edition), 2005, 26(1): 221–224. |
| [13] |
WU Yunkai, JIANG Bin, ZHOU Donghua, et al. Detection and isolation of multiple incipient sensor faults with application to high-speed railway traction motors[C]//Proceedings of CCC. USA: IEEE, 2016: 6558-6563. |
| [14] |
王洲辉, 张科, 韩治国.
基于鲁棒自适应观测器的线性系统故障估计[J]. 计算机仿真, 2016, 33(7): 131–134.
WANG Zhouhui, ZHANG Ke, HAN Zhiguo. Fault estimation based on the robust adaptive observer for linear system[J]. Computer Simulation, 2016, 33(7): 131–134. |
| [15] |
刘玲. 牵引变流器故障诊断的研究[D]. 成都: 西南交通大学, 2007.
LIU Ling. Research on fault diagnosis of traction converter[D]. Chengdu: Southwest Jiao Tong University, 2007. |
| [16] |
CAMPOS-DELGADO D U, ESPINOZA-TREJO D R.
An observer-based diagnosis scheme for single and simultaneous open-switch faults in induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 671–679.
DOI:10.1109/TIE.2010.2047829
|
| [17] |
刘春生, 汪芳, 胡寿松.
非线性系统的在线鲁棒故障检测[J]. 南京航空航天大学学报, 2001, 33(3): 263–266.
LIU Chunsheng, WANG Fang, HU Shousong. On line robust fault detection for nonlinear systems[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2001, 33(3): 263–266. |
| [18] |
KELIRIS C, POLYCARPOU M M, PARISINI T.
A robust nonlinear observer-based approach for distributed fault detection of input-output interconnected systems[J]. Automatica, 2015, 53: 408–415.
DOI:10.1016/j.automatica.2015.01.042
|
| [19] |
张绍杰, 刘春生, 胡寿松.
一类非线性系统的执行器组合故障自适应容错控制[J]. 系统工程与电子技术, 2010, 32(3): 634–637.
ZHANG Shaojie, LIU Chunsheng, HU Shousong. Adaptive fault tolerant control of actuator combination faults for a class of nonlinear systems[J]. Systems Engineering and Electronic Technology, 2010, 32(3): 634–637. |
| [20] |
MAO Z, ZHAN Y, TAO G, et al.
Sensor fault detection for rail vehicle suspension systems with disturbances and stochastic noises[J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 4691–4705.
DOI:10.1109/TVT.2016.2628054
|
| [21] |
韦徵, 陈轶涵, 龚春英, 等.
三相六开关VIENNA整流器功率开关开路故障诊断[J]. 南京航空航天大学学报, 2014, 46(1): 121–128.
WEI Zheng, CHEN Yihan, GONG Chunying, et al. Fault diagnosis of three phase six switch VIENNA rectifier power switch open circuit[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2014, 46(1): 121–128. |
| [22] |
SHAHNAZI R, ZHAO Q, SARI A H A, et al. Dynamic nonlinear unknown input observer for fault detection of induction motors[C]//Proceedings of ICEE. USA: IEEE, 2015: 823-828. |
 2018, Vol. 50
2018, Vol. 50