2. 机械工程国家级实验教学示范中心(山东大学), 济南, 250061
2. National Demonstration Center for Experimental Mechanical Engineering Education(Shandong University), Jinan, 250061, China
齿侧间隙、支承间隙与轮齿时变啮合刚度等非线性因素导致齿轮系统表现出强非线性特性, 引起系统出现混沌振动、噪声大、跳跃、精度降低等现象[1]。国内外学者在齿轮系统非线性方面做了大量地研究, Kahraman等[2]构建了一个三自由度齿轮系统非线性模型, 其中考虑了支承间隙、齿侧间隙等非线性因素, 同时研究了内部静态传动误差激励和外部激励之间的作用差别。考虑轴承变形引起的齿轮横向振动, Kim等[3]同样建立了三自由度齿轮传动系统非线性时变模型, 并分析了系统的动态响应。王三民等[4]建立了三自由度多间隙齿轮系统振动模型, 研究了系统在不同支撑条件下进入混沌的途径, 但齿侧间隙和支承间隙对混沌特性的影响没有进行分析。杨富春等[5]分析了多齿隙对两级直齿圆柱减速器系统非线性特性的影响, 但没有考虑支承间隙等因素对系统非线性特性的影响。考虑间隙、摩擦力和时变刚度的影响, Chen等[6]建立一个齿轮系统动力学模型, 并利用数值积分方法对系统运动状态进行预测。基于齿轮副扭转模型, Zhou等[7-8]分析了转速、齿侧间隙和阻尼系数对系统的动力学特性的影响。Farshidianfar等[9]在建立齿轮副系统非线性时变动力学模型时, 考虑齿侧间隙、时变刚度、外部激励等因素的影响。然后, 利用解析方法对系统的分岔特性与混沌现象进行了研究。盛冬平等[10]建立了四自由度齿轮副系统非线性振动模型, 研究了系统随转速、齿侧间隙、支承间隙等参数变化的分岔特性。根据含有齿侧间隙的多自由度模型, Gou等[11]利用胞映射方法对系统的分岔特性进行了分析。然而, 在不同载荷条件下, 考虑齿侧间隙和支承间隙的齿轮系统随非线性因素变化的分岔特性研究较少。
基于上述文献, 综合考虑时变啮合刚度、静态传动误差、齿侧间隙与支承间隙等非线性因素, 建立了齿轮副系统多自由度多间隙耦合非线性动力学模型, 并研究了在不同载荷条件下系统随非线性参数变化的动力学特性。
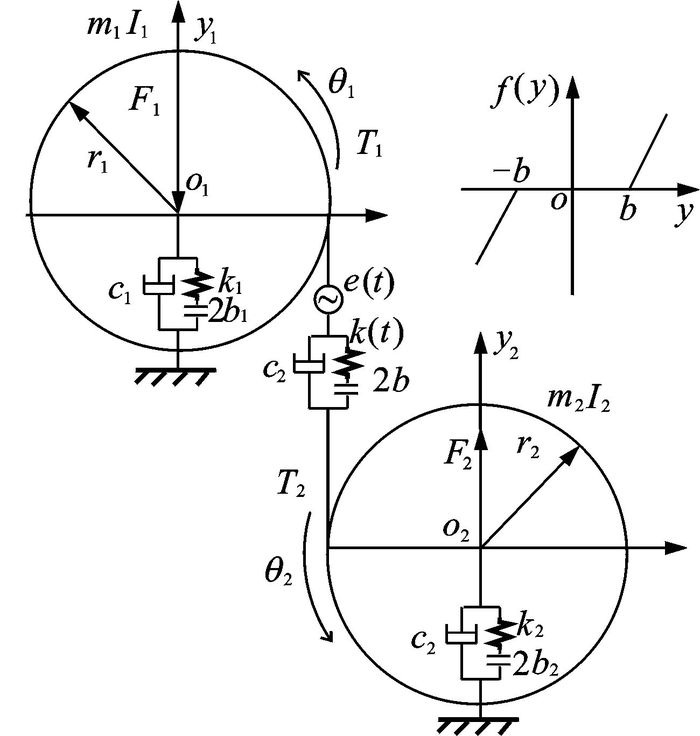
1 多间隙非线性动力学模型 1.1 系统的运动微分方程图 1为考虑静态传动误差、齿侧间隙、支承间隙及时变啮合刚度的直齿轮副系统动力学模型, 以啮合线方向为y轴建立坐标系, 每个齿轮均具有y方向和绕轴向的扭转自由度θ。图 1中, 主动齿轮1和被动齿轮2的质量分别为m1和m2; θ1和θ2分别为齿轮1和齿轮2的角位移; I1和I2分别为齿轮1和齿轮2的转动惯量; r1和r2分别为齿轮1和齿轮2的基圆半径; 齿轮i(i=1, 2) 的支承刚度、阻尼、支承间隙分别用ki, ci, 2bi表示; k(t), cm, 2b, e(t)分别为轮齿啮合副的啮合刚度、阻尼、齿侧间隙以及轮齿静态传动误差; F1和F2分别为作用在主从动轴上的轴承对齿轮的作用力; T1, T2为输入、输出转矩。
|
图 1 齿轮副多间隙非线性动力学模型 Figure 1 Nonlinear dynamic model of the gear pair system with multi-clearance |
忽略输出转矩的波动, 仅考虑静态传动误差和输入转矩波动引起的低频外激励导致的高频内部激励, 则
| $ \begin{array}{*{20}{c}} {{T_1}\left( t \right) = {T_{1m}} + {T_{1a}}\left( t \right)}\\ {{T_2}\left( t \right) = {T_{2m}}} \end{array} $ | (1) |
式中:T1(t)为输入扭矩, T2(t)为输出扭矩, T1m为输入扭矩的平均值, T2m为输出扭矩的平均值, T1a(t)为输入扭矩的波动部分。
齿轮系统扭转振动引起的相对振动位移yr可表示为
| $ {y_r} = {r_1}{\theta _1} - {r_2}{\theta _2} - e\left( t \right) $ | (2) |
式中e(t)为静态传动误差, 表达式为
| $ e\left( t \right) = \sum\limits_{r = 1}^\infty {{e_r}\sin \left( {r\omega t + {\varphi _r}} \right)} $ | (3) |
式中:er为误差幅值, φr为误差初始相位, 只考虑级数中基频的影响, 取r=1。
1.2 系统的动力学微分方程系统具有4个自由度, 其广义坐标为(θ1 , θ2 , y1, y2), 其中, θ1 , θ2分别为齿轮1、2的转动自由度, y1, y2分别为齿轮1、2的纵向自由度。根据牛顿第二定律, 可列出系统弯扭耦合的非线性动力学方程为
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{I_1}{{\ddot \theta }_1} + {r_1}{c_m}\left( {{{\dot y}_1} - {{\dot y}_2} + {{\dot y}_r}} \right) + }\\ {k\left( t \right)f\left( {{y_r},b} \right){r_1} = {T_1}} \end{array}\\ \begin{array}{*{20}{c}} {{I_2}{{\ddot \theta }_2} + {r_2}{c_m}\left( {{{\dot y}_2} - {{\dot y}_1} - {{\dot y}_r}} \right) - }\\ {k\left( t \right)f\left( {{y_r},b} \right){r_2} = - {T_2}} \end{array}\\ \begin{array}{*{20}{c}} {{m_1}{{\ddot y}_1} + {c_1}{{\dot y}_1} + {k_1}f\left( {{y_1},{b_1}} \right) = }\\ { - {F_1} - {c_m}\ddot y - k\left( t \right)f\left( {y,b} \right)} \end{array}\\ \begin{array}{*{20}{c}} {{m_2}{{\ddot y}_2} + {c_2}{{\dot y}_{22}} + {k_2}f\left( {{y_2},{b_2}} \right) = }\\ {{F_2} + {c_m}\ddot y + k\left( t \right)f\left( {y,b} \right)} \end{array} \end{array} \right. $ | (4) |
在轮齿啮合过程中, 参与啮合的轮齿对数交替变化, 存在着单齿啮合与双齿啮合, 导致齿轮副啮合刚度的周期变化。齿轮副时变啮合刚度k(t)用傅里叶级数以啮合频率展开
| $ k\left( t \right) = {k_m} + \sum\limits_{r = 1}^\infty {{k_{hr}}\cos \left( {r\omega t + {\varphi _{hr}}} \right)} $ | (5) |
式中:km为平均啮合刚度, khr为各谐波分量的刚度幅值, ω为啮合频率, φhr为啮合刚度初始变化的初相位, 只考虑级数中基频的影响, 取r=1。
齿轮啮合副的动态啮合力Fm可以表示为
| $ {F_m} = {c_m}\dot y + k\left( t \right)f\left( {y,b} \right) $ | (6) |
式中cm为啮合阻尼, f(y, b)为间隙函数。
| $ {c_m} = 2\xi \sqrt {{k_m}/\left( {1/{m_1} + 1/{m_2}} \right)} $ | (7) |
式中ξ为啮合副相对阻尼比。
齿轮副系统间隙非线性函数f(y, b)可表示为
| $ f\left( {y,b} \right) = \left\{ {\begin{array}{*{20}{c}} {y - b}&{y > b}\\ 0&{\left| y \right| \le b}\\ {y + b}&{y < - b} \end{array}} \right. $ | (8) |
式中b为半齿侧间隙。
而径向支承间隙非线性函数fi(Yi, bi)[4]分别为
| $ {f_1}\left( {{y_i},{b_i}} \right) = \left\{ {\begin{array}{*{20}{c}} {{y_i} - {b_i}}&{{y_i} > {b_i}}\\ 0&{\left| {{y_i}} \right| \le {b_i}}\\ {{y_i} + {b_i}}&{{y_i} < - {b_i}} \end{array}\left( {i = 1,2} \right)} \right. $ | (9) |
式中bi (i=1, 2) 分别为主从动轮半支承间隙。
由于间隙的存在, 使得系统约束不完整, 式(4) 为半正定系统, 存在着刚体位移[10]。为了消除刚体位移, 引入相对坐标使方程降维。以相对坐标y作为广义坐标, y可表示为
| $ y = {y_r} + {y_1} - {y_2} $ | (10) |
则方程(4) 可转化为
| $ \left\{ \begin{array}{l} \ddot y + \left( {\frac{1}{{{m_e}}} + \frac{1}{{{m_1}}} + \frac{1}{{{m_2}}}} \right){c_m}\dot y + \frac{{{c_1}}}{{{m_1}}}{{\dot y}_1} - \frac{{{c_2}}}{{{m_2}}}{{\dot y}_2} + \\ \;\;\;\left( {\frac{1}{{{m_e}}} + \frac{1}{{{m_1}}} + \frac{1}{{{m_2}}}} \right)k\left( t \right)f\left( {y,b} \right) + \frac{{{k_1}}}{{{m_1}}}{f_1}\left( {{y_1},{b_1}} \right) - \\ \;\;\;\frac{{{k_2}}}{{{m_2}}}{f_2}\left( {{y_2},{b_2}} \right) = \frac{F}{{{m_e}}} + \frac{{{r_1}{T_{1a}}}}{{{I_1}}} + {e_r}{\omega ^2}\cos \left( {\omega t} \right)\\ {{\ddot y}_1} + \frac{{{c_1}}}{{{m_1}}}{{\dot y}_1} + \frac{{{k_1}}}{{{m_1}}}{f_1}\left( {{y_1},{b_1}} \right) = - \frac{{{F_1}}}{{{m_1}}} - \frac{{{c_m}}}{{{m_1}}}y - \\ \;\;\;\;\frac{{k\left( t \right)}}{{{m_1}}}f\left( {y,b} \right)\\ {{\ddot y}_2} + \frac{{{c_2}}}{{{m_2}}}{{\dot y}_2} + \frac{{{k_2}}}{{{m_2}}}{f_2}\left( {{y_2},{b_2}} \right) = \frac{{{F_2}}}{{{m_2}}} + \frac{{{c_m}}}{{{m_2}}}y + \\ \;\;\;\;\frac{{k\left( t \right)}}{{{m_2}}}f\left( {y,b} \right) \end{array} \right. $ | (11) |
式中:F=T1m/r1=T2m/r2, 齿轮副等效质量me=I1I2/(I1r12+I2r22)。
1.3 系统的量纲一方程在系统运动方程中, 参数数值间差别较大, 有必要对方程进行量纲化处理。定义量纲-时间τ=ωnt, 其中
量纲-间隙非线性函数分别为
| $ f\left( {Y,B} \right) = \left\{ {\begin{array}{*{20}{c}} {Y - B}&{Y > B}\\ 0&{\left| Y \right| \le B}\\ {Y + B}&{Y < - B} \end{array}} \right. $ | (12) |
| $ {f_i}\left( {{Y_i},{D_i}} \right) = \left\{ {\begin{array}{*{20}{c}} {{Y_i} - {D_i}}&{{Y_i} > {D_i}}\\ 0&{\left| {{Y_i}} \right| \le {D_i}}\\ {{Y_i} + {D_i}}&{{Y_i} < - {D_i}} \end{array}\left( {i = 1,2} \right)} \right. $ | (13) |
式中:B=b/bc和Di=bi/bc(i=1, 2)。
将以上各式代入式(11) 中可以得到消除刚体位移以及量纲化的系统动力学微分方程, 并整理为矩阵形式, 即
| $ \mathit{\boldsymbol{M\ddot X}} + \mathit{\boldsymbol{C\dot X}} + \mathit{\boldsymbol{KX}} = \mathit{\boldsymbol{F}} $ | (14) |
式中:M, C, K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵, F为激励力向量, X为位移向量。各个矩阵和向量的表达式如下
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right],\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{\zeta _{11}}}&{{\zeta _{12}}}&{{\zeta _{13}}}\\ {{\zeta _{21}}}&{{\zeta _{22}}}&0\\ {{\zeta _{31}}}&0&{{\zeta _{33}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{K = }}\left[ {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}\\ {{k_{21}}}&{{k_{22}}}&0\\ {{k_{31}}}&0&{{k_{33}}} \end{array}} \right],\mathit{\boldsymbol{F}} = {\left\{ {\begin{array}{*{20}{c}} {{{\bar F}_s}}&{{{\bar F}_1}}&{{{\bar F}_2}} \end{array}} \right\}^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{X}} = {\left\{ {\begin{array}{*{20}{c}} Y&{{Y_1}}&{{Y_2}} \end{array}} \right\}^{\rm{T}}} $ |
式中:
| $ {\zeta _{11}} = \left( {\frac{1}{{{m_e}}} + \frac{1}{{{m_1}}} + \frac{1}{{{m_2}}}} \right)\frac{{{c_m}}}{{{\omega _n}}},{\zeta _{12}} = \frac{{{c_1}}}{{{m_1}{\omega _n}}}, $ |
| $ \begin{array}{l} {\zeta _{13}} = - \frac{{{c_2}}}{{{m_2}{\omega _n}}},{\zeta _{21}} = \frac{{{c_m}}}{{{m_1}{\omega _n}}},{\zeta _{22}} = \frac{{{c_1}}}{{{m_1}{\omega _n}}},{\zeta _{31}} = - \\ \frac{{{c_m}}}{{{m_2}{\omega _n}}},{\zeta _{33}} = \frac{{{c_2}}}{{{m_2}{\omega _n}}},{k_{33}} = \frac{{{k_2}}}{{{m_2}\omega _n^2}},{k_{11}} = \left( {\frac{1}{{{m_e}}} + \frac{1}{{{m_1}}} + \frac{1}{{{m_2}}}} \right)\\ \frac{{k\left( \tau \right)}}{{\omega _n^2}},{k_{12}} = \frac{{{k_1}}}{{{m_1}\omega _n^2}},{k_{13}} = - \frac{{{k_2}}}{{{m_2}\omega _n^2}},{k_{21}} = \frac{{k\left( \tau \right)}}{{{m_1}\omega _n^2}},{k_{22}} = \\ \frac{{{k_1}}}{{{m_1}\omega _n^2}},{k_{31}} = - \frac{{k\left( \tau \right)}}{{{m_2}\omega _n^2}},{{\bar F}_1} = - \frac{{{F_1}}}{{{b_c}{m_1}\omega _n^2}}, \end{array} $ |
| $ \begin{array}{l} {{\bar F}_2} = \frac{{{F_2}}}{{{b_c}{m_2}\omega _n^2}},{{\bar F}_a} = \frac{{{r_1}{T_{1a}}}}{{{b_c}{I_1}\omega _n^2}},\bar F = \frac{F}{{{b_c}{m_e}\omega _n^2}},{{\bar F}_s} = \bar F + \\ {{\bar F}_a} + {{\bar F}_{ah}},{F_{ah}} = \frac{{{e_r}}}{{{b_c}}},{{\bar F}_{ah}} = {F_{ah}}{\mathit{\Omega }^2}\cos \left( {\mathit{\Omega }\tau } \right). \end{array} $ |
齿轮系统相关计算参数:模数m=3 mm, 齿数z1=z2=40, 压力角α=20°, bc=0.1 mm, 平均啮合刚度km=2×109。采用数值积分方法对方程进行求解。基于系统在不同参数下的分岔图, 分析非线性因素对系统运动特性的影响。
齿轮系统在不同的工况下, 其负载情况是变化的。载荷比的大小反映了齿轮系统的承载情况, 载荷比大时, 系统承载能力大; 反之, 系统承载能力小。因此, 在研究非线性参数对系统运动特性影响时, 需要在重载和轻载两种情况下分别进行讨论分析。
2.1 齿侧间隙B对系统分岔特性的影响在重载条件和轻载条件下, 分别研究系统在阻尼比ξ为0.02, 0.04, 0.06和0.08下的量纲-相对位移Y随量纲-齿侧间隙B变化的分岔特性, 如图 2, 3所示。
|
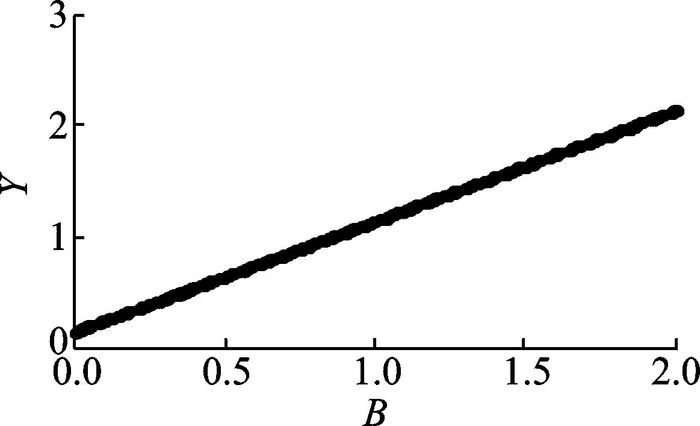
图 2 在重载条件下, 系统随齿侧间隙B变化的分岔图 Figure 2 Under heavily loaded condition, bifurcation diagrams of B versus Y |

|
图 3 齿侧间隙B=0.15时, 系统动力学响应曲线 Figure 3 Dynamic response curves of system when B=0.15 |
(1) 重载条件下
从图 2可以看出, 随着量纲-齿侧间隙B的变化, 系统一直处于单周期运动状态。取齿侧间隙B为0.15, 相应的相图和Poincaré图如图 3所示, 表明系统处于单周期运动。在重载条件下, 齿侧间隙并不影响系统的周期性运动特性, 只改变了系统的运动幅值。
(2) 轻载条件下
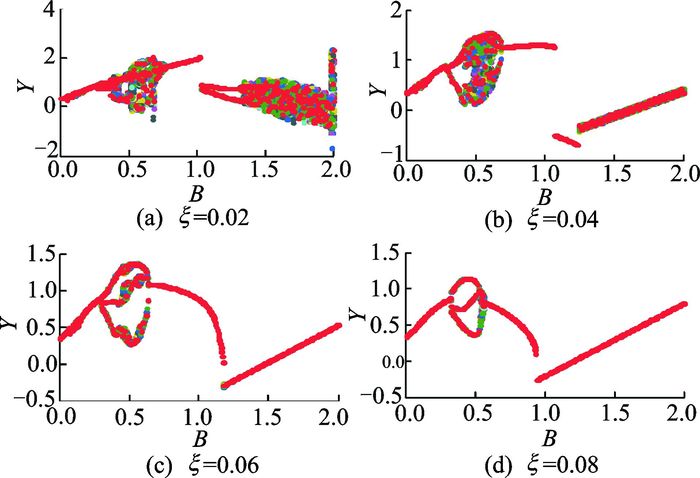
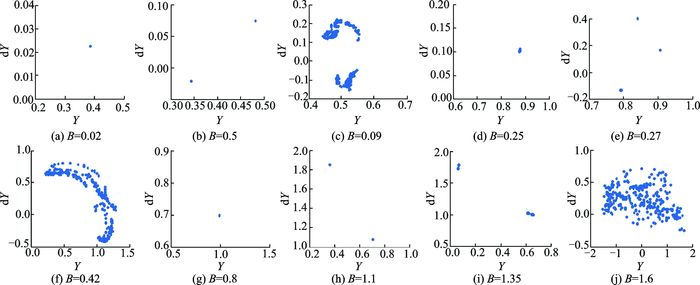
图 4给出了在不同阻尼比下系统随量纲-齿侧间隙B变化的分岔图。随着齿侧间隙的变化, 系统的运动状态表现出丰富性和复杂性。从图 4(a)可以看出, 在齿侧间隙B取初始值时, 系统处于周期运动状态。相应地间隙B分别取0.02和0.05时, 则Poincaré图中显示为单点和两点, 如图 5(a, b)所示, 表明系统位于单周期和两周期运动。齿侧间隙B继续增大, 系统从周期运动进入混沌运动, 如图 5(c)所示。随后, 系统又一次进入周期运动, 单周期运动和三周期运动, 如图 5(d, e)所示。之后, 齿侧间隙B保持增大, 系统重新进入混沌运动, 如图 5(f)所示。然后, 系统再一次进入周期运动。然而, 系统从单周期运动经由激变进入两周期运动, 如图 5(g, h)所示。同时, 通过倍分岔形式进入四周期运动, 如图 5(i)所示。最后, 当量纲-齿侧间隙达到一定值时, 系统一直处于混沌运动。
|
图 4 轻载条件下, 系统在不同阻尼比下随B变化的分岔图 Figure 4 Under lightly loaded condition, bifurcation diagrams of B versus Y at different ξ |
|
图 5 系统在不同量纲-齿侧间隙B下的Poincaré映射图 Figure 5 Poincaré maps of Y versus dY at different B |
而当阻尼比从0.02增大到0.08时, 图 4中的混沌区间逐渐减小, 而且振动幅值减小。说明当阻尼增大时, 系统趋于稳定, 但系统消耗的能量会增大。对于机械系统而言, 混沌运动预示着系统的不稳定, 不可控。因此在齿轮传动中, 应选取合适的齿侧间隙值, 避免系统混沌运动的产生, 保证系统的正常运转。
2.2 支承间隙D对系统动力学响应的影响(1) 重载条件下
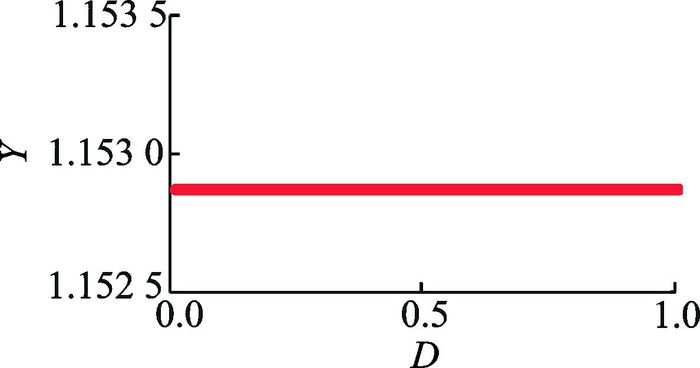
在重载条件下, 量纲-支承间隙D对系统的运动特性影响较弱。随着量纲-支承间隙D的变化, 相对位移Y保持不变, 如图 6所示。
|
图 6 重载条件下, 系统随支承间隙D变化的分岔图 Figure 6 Under heavily loaded condition, bifurcation diagrams of D versus Y |
选取支承间隙D为0.1, 图 7为系统的相图和Poincaré图, 相图曲线为一个椭圆, 而Poincaré图中仅有一个单点, 表明系统处于单周期运动。因此, 在重载条件下, 支承间隙对系统啮合线上的运动影响较小。
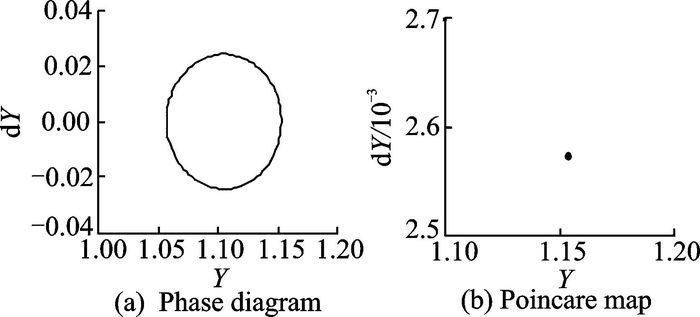
|
图 7 支承间隙D=0.1时, 系统动力学响应曲线 Figure 7 Dynamic response curves of system when D=0.1 |
(2) 轻载条件下
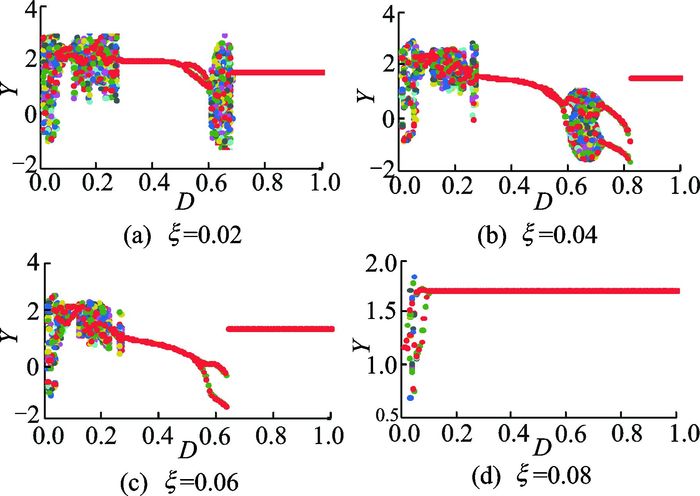
在轻载条件下, 量纲-支承间隙D变化时, 系统表现出丰富的运动状态(图 8)。在阻尼比ξ=0.02时, 支承间隙取值较小时, 例如当D=0.03时, Poincaré图为具有分形结构的离散点, 系统处于混沌运动, 如图 9(a)所示。之后, 系统进入一个狭小的周期运动阶段, 如图 9(b)所示。然后, 系统重新进入混沌运动, 见图 9(c)。随着支承间隙的增大, 系统从混沌运动进入周期运动状态, 单周期运动和两周期运动, 见图 9(d, e)。支承间隙继续增大, 系统再次进入混沌运动。最后, 系统稳定在单周期运动状态, 如图 9(g)所示。相比图 4(a), 图 4(b~d)中的混沌区间窗口逐渐减小, 甚至当阻尼比ξ=0.1时, 系统仅有周期运动状态。说明增大系统的阻尼比可以有效减小混沌区间, 保证较大的稳定区间。因此, 在选取支承间隙时, 应避开可能的混沌区间, 使得系统稳定良好地运行。
|
图 8 轻载条件下, 系统在不同阻尼比下随支承间隙D变化的分岔图 Figure 8 Under lightly loaded condition, bifurcation diagrams of D versus Y at different ξ values |
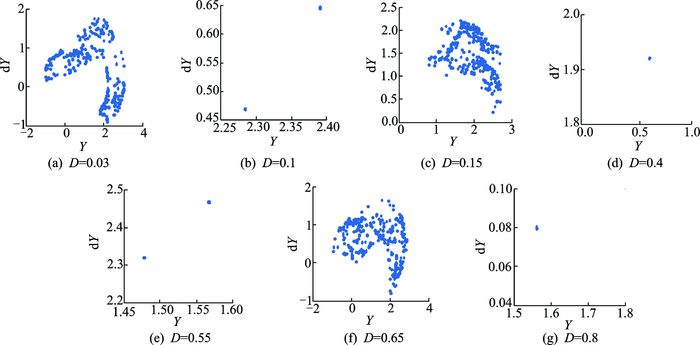
|
图 9 系统在不同量纲-支承间隙D下的Poincaré映射图 Figure 9 Poincaré maps of Y versus dY at different D values |
3 结论
(1) 本文建立了考虑多间隙的齿轮系统非线性动力学模型。通过引入相对扭转位移作为新的广义坐标, 同时利用数值积分方法对系统方程进行求解, 研究了系统在不同载荷条件下随齿侧间隙、支承间隙与阻尼比变化的非线性动力学特性。
(2) 系统在重载条件下随着齿侧间隙的变化, 其周期性运动特性没有变化, 但振动幅值增大。在轻载条件下, 系统运动变化过程中有激变状态出现, 且随着阻尼的增大, 混沌运动区间逐渐变小。
(3) 在重载条件下, 支承间隙变化时, 系统处于单周期状态, 且运动幅值不变, 说明支承间隙对啮合线上的运动影响较小。而在轻载条件下, 系统的运动状态较丰富, 包括单周期、多周期和混沌运动。而且随着阻比的增大, 混沌区间逐渐变窄。因此, 在设计与控制齿轮系统的运动状态时, 应合理选取系统参数, 避免系统处于混沌状态。
| [1] |
李润方, 王建军.
齿轮系统动力学——振动、冲击、噪声[M]. 北京: 科学出版社, 1997.
LI Runfang, WANG Jianjun. Gear system dynamics—Vibration, shock, noise[M]. Beijing: Science Press, 1997. |
| [2] | KAHRAMAN A, SINGH R. Non-linear dynamics of a geared rotor-bearing system with multiple clearances[J]. Journal of Sound and Vibration, 1991, 144(3): 469–506. DOI:10.1016/0022-460X(91)90564-Z |
| [3] | KIM W, Hong H Y, CHUNG J. Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation[J]. Journal of Sound and Vibration, 2010, 329(21): 4409–4421. DOI:10.1016/j.jsv.2010.04.026 |
| [4] |
王三民, 沈允文, 董海军.
多间隙耦合非线性动力系统的分叉与混沌[J]. 西北工业大学学报, 2003, 21(2): 191–194.
WANG Sanmin, SHEN Yunwen, DONG Haijun. Bifurcation and chaos in a nonlinear dynamic with multiple clearances and time-varying stiffness[J]. Journal of Northwestern Polytechnic University, 2003, 21(2): 191–194. |
| [5] |
杨富春, 周晓军, 胡宏伟.
两级齿轮减速器非线性振动特性研究[J]. 浙江大学学报:工学版, 2009(7): 1243–1248.
YANG Fuchun, ZHOU Xiaojun, HU Hongwei. Nonlinear vibration characteristics of two-stage gear reducer[J]. Journal of Zhejiang University: Engineering Science, 2009(7): 1243–1248. |
| [6] | CHEN S Y, TANG J Y, LUO C W. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction[J]. Mechanism and Machine Theory, 2011, 46(4): 466–478. DOI:10.1016/j.mechmachtheory.2010.11.016 |
| [7] | LIU J, WANG S J, ZHOU S H. Nonlinear behavior of a spur gear pair transmission system with backlash[J]. Journal of Vibroengineering, 2014, 16(8): 3922–3938. |
| [8] | ZHOU S H, LIU J, LI C F. Nonlinear behavior of a spur gear pair transmission system with backlash[J]. Journal of Vibroengineering, 2014, 16(8): 3850–3861. |
| [9] | FARSHIDIANFAR A, SAGHAFI A. Global bifurcation and chaos analysis in nonlinear vibration of spur gear systems[J]. Nonlinear Dynamics, 2014, 75: 783–806. DOI:10.1007/s11071-013-1104-4 |
| [10] |
盛冬平, 朱如鹏, 陆凤霞.
多间隙弯扭耦合齿轮非线性振动的分岔特性研究[J]. 振动与冲击, 2014, 33(19): 116–122.
SHENG Dongping, ZHU Rupeng, LU Fengxia. Bifurcation characteristics of bending-torsional coupled nonlinear vibration with multi-clearanyce[J]. Journal of Vibration and Shock, 2014, 33(19): 116–122. |
| [11] | GOU X F, ZHU L Y, CHEN D L. Bifurcation and chaos analysis of spur gear pair in two-parameter plane[J]. Nonlinear Dynamics, 2015, 79(3): 2225–2235. DOI:10.1007/s11071-014-1807-1 |
 2017, Vol. 49
2017, Vol. 49


