在过去的二十多年里,格子波尔兹曼方法(Lattice Boltzmann method,LBM)已被广泛地用于模拟研究多种流体力学问题[1]。在历史发展的过程中,LBM是由格子气自动机(Lattice gas automata,LGA)演化而来的[2];但随后证明,它也可以看作是波尔兹曼方程的一种特殊的离散格式[4]。格子波尔兹曼方程(Lattice Boltzmann equation,LBE)是一种形式非常简单的代数方程,它包含两个简单的连续变化过程:迁移和碰撞。LBE中唯一的变量是粒子分布函数(Particle distribution function,PDF),通过对PDF进行求和就可以得到宏观变量。
标准LBM使用的网格必须是均匀的,而且时间步长由网格步长确定,这在很大程度限制了LBM的应用范围。究其原因是因为在波尔兹曼方程离散至LBE过程中,物理空间的离散和粒子速度空间的离散是耦合在一起完成的[3]。但事实上,它们之间可以相互解耦[4]。为此,可以先进行粒子速度空间的离散,从而得到离散波尔兹曼方程(Discrete Boltzmann equation,DBE)。在此基础上,使用传统的数值方法对DBE进行空间的离散求解。目前,已形成了基于有限差分、有限体积和有限元的一系列格子波尔兹曼方法(Finite difference-lattice Boltzmann method,FD-LBM[5], Finite volume-lattice Boltzmann method,FV-LBM[6], Finite element-lattice Boltzmann method,FE-LBM[7]), 这些方法不再受制于均匀网格而能灵活地利用各种不同的非均匀网格。
另一方面,间断有限元(Discontinuous Galerkin,DG)法[8]近年来已开始逐步被用于求解流体力学问题。它在保留了有限元法的高精度格式的基础上,引入了有限体积法的数值通量的概念。因此,它同时拥有了这两种方法的优点。最近,DG方法也被用来求解LBE或DBE。基于改进的Dubiners三角基函数,Shi等[9]采用DG谱单元方法求解LBE并模拟了低雷诺数(Re≤200)的圆柱绕流问题。采用形状函数,Duster等[10]在四边形单元上用DG求解DBE,同时采用一阶欧拉格式进行时间离散。Min和Lee[11]则在四边形单元上用DG谱单元方法求解LBE。此外,他们把LBE中的碰撞过程和迁移过程分开处理,从而提高了LBM在模拟高雷诺数问题时的稳定性。虽然二维质量矩阵在他们的方法中可以对角化,但是该方法仅限于在四边形单元上使用。
基于节点间断有限元(Nodal discontinuous Galerkin,NDG)方法[12],本文提出了一种求解LBE的新方法,即节点间断有限元-格子波尔兹曼方法(Nodal discontinuous Galerkin-lattice Boltzmann method,NDG-LBM)。借鉴Min和Lee[11]的思想,LBE的碰撞过程和迁移过程被拆分成了两步。碰撞过程用LBM种的多松弛时间(Multiple relaxation time,MRT)模型[13]进行求解,而迁移过程则可以写成对流方程并采用NDG方法进行求解。其中,空间离散采用了非结构网格,时间离散采用了四阶、五步龙格-库塔格式。本文介绍了LBM中的MRT模型和NDG-LBM并给出了采用该方法模拟顶盖方腔驱动流、静止单个圆柱绕流、旋转-静止双圆柱绕流以及高雷诺数NACA0012翼型绕流的计算结果及相应的分析。
1 数值方法 1.1 格子波尔兹曼方程对于二维黏性不可压流,可以用格子波尔兹曼方程表示
| $ \begin{array}{*{20}{c}} {{f_\alpha } = \left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_\alpha }\delta t,t + \delta t} \right) = }\\ {{f_\alpha }\left( {\mathit{\boldsymbol{x}},t} \right) - \frac{1}{\tau }\left[ {{f_\alpha }\left( {\mathit{\boldsymbol{x}},t} \right) - f_\alpha ^{{\rm{eq}}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right]} \end{array} $ | (1) |
式中:fα为密度分布函数;fαeq为其相应的平衡状态;τ为单松弛时间系数;eα为粒子速度;t为时间;δt为时间步长;x为位置;在本文的数值模拟中,采用的是D2Q9粒子速度模型,所以粒子速度eα为
| $ {\mathit{\boldsymbol{e}}_\alpha } = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\left( {0,0} \right)}\\ {\left( { \pm 1,0} \right),\left( {0, \pm 1} \right)}\\ {\left( { \pm 1, \pm 1} \right)} \end{array}}&{\begin{array}{*{20}{c}} {\alpha = 0}\\ {\alpha = 1 \sim 4}\\ {\alpha = 5 \sim 8} \end{array}} \end{array}} \right. $ | (2) |
平衡分布函数为
| $ f_\alpha ^{{\rm{eq}}}\left( {\mathit{\boldsymbol{x}},t} \right) = \rho {w_\alpha }\left[ {1 + \frac{{{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{u}}}}{{c_s^2}} + \frac{{{{\left( {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{u}}} \right)}^2} - {{\left( {{c_s}\left| \mathit{\boldsymbol{u}} \right|} \right)}^2}}}{{2c_s^4}}} \right] $ | (3) |
式中:ρ为密度;cs为LBM中的声速;cs2=
当LBM采用单松弛时间(Single relaxation time,SRT)模型,数值模拟在某些情况下会变得不稳定。为了克服这个困难,Lallemand和Luo[13]采用的方法是把不同的物理量如动量、能量等在动量空间分开处理,使用不同的松弛时间系数使它们各自松弛到相应的平衡状态。因此,本文引入了多松弛时间模型以提高计算稳定性,进而保证计算的准确性,式(1)则可改写为
| $ \begin{array}{*{20}{c}} {{f_\alpha } = \left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_\alpha }\delta t,t + \delta t} \right) = }\\ {{f_\alpha }\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{S}}\left[ {\mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{R}}^{{\rm{eq}}}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right]} \end{array} $ | (4) |
式中:R为fα在动量空间上的一组物理量,Req为其相应的平衡态,它们的表达式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{R}} = {{\left\{ {\rho ,e,\varepsilon ,{j_x},{q_x},{j_y},{q_y},{p_{xx}},{p_{xy}}} \right\}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{R}}^{{\rm{eq}}}} = {{\left\{ {0,{e^{{\rm{eq}}}},{\varepsilon ^{{\rm{eq}}}},0,q_x^{{\rm{eq}}},0,q_y^{{\rm{eq}}},p_{xx}^{{\rm{eq}}},p_{xy}^{{\rm{eq}}}} \right\}}^{\rm{T}}}} \end{array} $ | (5a) |
| $ \begin{array}{*{20}{c}} {{e^{{\rm{eq}}}} = - 2\rho + 3\left( {j_x^2 + j_y^2} \right)/\rho }\\ {{\varepsilon ^{{\rm{eq}}}} = \rho - 3\left( {j_x^2 + j_y^2} \right)/\rho }\\ {q_x^{{\rm{eq}}} = - {j_x},q_y^{{\rm{eq}}} = - {j_y}}\\ {p_{xx}^{{\rm{eq}}} = \left( {j_x^2 - j_y^2} \right)/\rho ,p_{xy}^{{\rm{eq}}} = {j_x}{j_y}/\rho } \end{array} $ | (5b) |
式中:在R空间中,ρ为密度,e为能量,ε为能量的平方,jx和jy分别为x和y方向的动量分量(ρu和ρv),qx和qy分别为相应的能量通量,pxx和pxy则为应力张量,M为把fα转化到R空间的相应的转化矩阵
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} 1&1&1&1&1&1&1&1&1\\ { - 4}&{ - 1}&{ - 1}&{ - 1}&{ - 1}&2&2&2&2\\ 4&{ - 2}&{ - 2}&{ - 2}&{ - 2}&1&1&1&1\\ 0&1&0&{ - 1}&0&1&{ - 1}&{ - 1}&1\\ 0&{ - 2}&0&2&0&1&{ - 1}&{ - 1}&1\\ 0&0&1&0&{ - 1}&1&1&{ - 1}&{ - 1}\\ 0&0&{ - 2}&0&2&1&1&{ - 1}&{ - 1}\\ 0&1&{ - 1}&1&{ - 1}&0&0&0&0\\ 0&0&0&0&0&1&{ - 1}&1&{ - 1} \end{array}} \right] $ |
此外,S是一个非负的对角矩阵,S=diag(0, s1, s2, 0, s4, 0, s6, s7, s8),其值可以通过线性稳定性分析获得[13]。在本文的模拟中,这些值分别取为s1=1.6, s2=1.4, s4=s6=1.2, s7=s8=1/τ。其中τ=υ/(cs2δt)+0.5,υ为流体运动黏度。
LBE包含两个过程:碰撞过程和迁移过程。它们在实际求解时可以分开来处理,即
碰撞过程
| $ {{\tilde f}_\alpha }\left( {\mathit{\boldsymbol{x}},t} \right) = {f_\alpha }\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{S}}\left[ {\mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{R}}^{{\rm{eq}}}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right] $ | (6a) |
迁移过程
| $ {f_\alpha }\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_\alpha }\delta t,t + \delta t} \right) = {{\tilde f}_\alpha }\left( {\mathit{\boldsymbol{x}},t} \right) $ | (6b) |
方程式(6b)实际上是对流方程的数值离散表达式。为了保持计算的稳定性,它要求采用均匀的直角网格并且CFL数必须为1。为了消除这些限制,可以把迁移过程还原为对流方程
| $ \frac{{\partial {f_\alpha }}}{{\partial t}} + \left( {{\mathit{\boldsymbol{e}}_\alpha } \cdot \nabla } \right){f_\alpha } = 0 $ | (7) |
随后,可以采用不同的数值方法来求解方程式(7)。本文采用的方法是节点间断有限元法。
1.2 节点间断有限元方法如果定义通量Fα(f)=eαfα,方程式(7)则可改写为
| $ \frac{{\partial {f_\alpha }}}{{\partial t}} + \nabla \cdot {\mathit{\boldsymbol{F}}_\alpha }\left( f \right) = 0 $ | (8) |
与所有的有限元方法一样,可以把计算区域Ω离散成一些不重叠的子区域Ωk(或称之为单元)。因此有
| $ \int_{{\mathit{\Omega }^k}} {\left[ {\frac{{\partial {f_\alpha }}}{{\partial t}} + \nabla \cdot {\mathit{\boldsymbol{F}}_\alpha }\left( f \right)} \right]\varphi {\rm{d}}\mathit{\Omega }} = 0 $ | (9) |
对式(9)中的通量项进行部分积分,则有
| $ \begin{array}{*{20}{c}} {\int_{{\mathit{\Omega }^k}} {\frac{{\partial {f_\alpha }}}{{\partial t}}\varphi {\rm{d}}\mathit{\Omega }} - \int_{{\mathit{\Omega }^k}} {{\mathit{\boldsymbol{F}}_\alpha }\left( f \right) \cdot \nabla \varphi {\rm{d}}\mathit{\Omega }} = }\\ { - \int_{{\mathit{\Gamma }^k}} {\varphi \mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{F}}_\alpha }\left( f \right){\rm{d}}\mathit{\Gamma }} } \end{array} $ | (10) |
式中:Γk为单元Ωk的边界,n为边界的单元外法向量。在DG中,两个相邻单元的界面上fα的值可以是不连续的。这样,可以定义fα-为当前单元的界面上的值而fα+为相邻单元的界面上的值。因此,可以定义数值通量Fα*(f)=Fα*(f-, f+),并用其表示相邻单元界面上的通量。方程式(10)可写为
| $ \begin{array}{*{20}{c}} {\int_{{\mathit{\Omega }^k}} {\frac{{\partial {f_\alpha }}}{{\partial t}}\varphi {\rm{d}}\mathit{\Omega }} - \int_{{\mathit{\Omega }^k}} {{\mathit{\boldsymbol{F}}_\alpha }\left( f \right) \cdot \nabla \varphi {\rm{d}}\mathit{\Omega }} = }\\ { - \int_{{\mathit{\Gamma }^k}} {\varphi \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{F}}_\alpha ^ * \left( f \right){\rm{d}}\mathit{\Gamma }} } \end{array} $ | (11) |
对式(11)再次进行部分积分,则有
| $ \begin{array}{l} \int_{{\mathit{\Omega }^k}} {\left[ {\frac{{\partial {f_\alpha }}}{{\partial t}} + \nabla \cdot {\mathit{\boldsymbol{F}}_\alpha }\left( f \right)} \right]\varphi {\rm{d}}\mathit{\Omega }} = \\ \int_{{\mathit{\Gamma }^k}} {\varphi \mathit{\boldsymbol{n}} \cdot \left[ {{\mathit{\boldsymbol{F}}_\alpha }\left( f \right) - \mathit{\boldsymbol{F}}_\alpha ^ * \left( f \right)} \right]{\rm{d}}\mathit{\Gamma }} \end{array} $ | (12) |
式(12)就是本文用来处理LBM中迁移过程的基本方程。
目前,已有了若干种不同的数值通量格式。本文采用考虑了逆风影响的Lax-Friedrichs格式,即
| $ \mathit{\boldsymbol{F}}_\alpha ^ * \left( {{f^ - },{f^ + }} \right) = \frac{1}{2}\left[ \begin{array}{l} {\mathit{\boldsymbol{F}}_\alpha }\left( {{f^ - }} \right) + {\mathit{\boldsymbol{F}}_\alpha }\left( {{f^ + }} \right) + \\ \left| \mathit{\Lambda } \right|\left( {f_\alpha ^ - ,f_\alpha ^ + } \right)\mathit{\boldsymbol{n}} \end{array} \right] $ | (13) |
式中:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{n}} \cdot \left[ {{\mathit{\boldsymbol{F}}_\alpha } - \mathit{\boldsymbol{F}}_\alpha ^ * } \right] = \frac{1}{2}\left( {\mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{e}}_\alpha } - \left| {\mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{e}}_\alpha }} \right|} \right)\left( {f_\alpha ^ - - f_\alpha ^ + } \right) = }\\ {\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\left( {\mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{e}}_\alpha }} \right)\left( {f_\alpha ^ - - f_\alpha ^ + } \right)}\\ 0 \end{array}}&{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{e}}_\alpha } < 0}\\ {\mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{e}}_\alpha } \ge 0} \end{array}} \end{array}} \right.} \end{array} $ | (14) |
在NDG[16]中,fα在每个单元Ωk内可以近似地表示为
| $ \begin{array}{*{20}{c}} {f_\alpha ^k\left( {\mathit{\boldsymbol{x}},t} \right) \approx \hat f_\alpha ^k\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_{n = 1}^{{N_p}} {\hat f_{\alpha ,n}^k\left( t \right){\psi _n}\left( \mathit{\boldsymbol{x}} \right)} = }\\ {\sum\limits_{n = 1}^{{N_p}} {\hat f_\alpha ^k\left( {{\mathit{\boldsymbol{x}}_n},t} \right)\ell _n^k\left( \mathit{\boldsymbol{x}} \right)} } \end{array} $ | (15) |
式中:
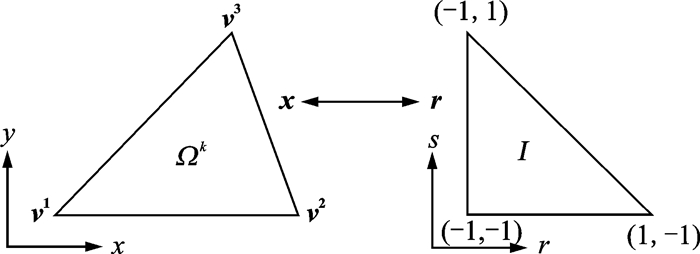
用来离散计算区域的三角形Ωk通常没有固定的形状,为了便于生成三角形单元内的节点,可以把普通三角形Ωk={x=(x, y)}转化成标准三角形I={r=(r, s)|r, s≥-1;r+s≤0,如图 1所示。
|
图 1 普通三角形Ωk和标准三角形I之间的关系 Figure 1 Relationship between general triangle Ωk and standard triangle I |
因此,它们之间的关系为[16]
| $ \mathit{\boldsymbol{x}} = - \frac{{r + s}}{2}{\mathit{\boldsymbol{v}}^1} + \frac{{r + 1}}{2}{\mathit{\boldsymbol{v}}^2} + \frac{{s + 1}}{2}{\mathit{\boldsymbol{v}}^3} $ | (16) |
式中:v1,v2和v3为三角形顶点的向量,它们以逆时针方向排序。有如下等式
| $ \frac{{\partial \mathit{\boldsymbol{x}}}}{{\partial \mathit{\boldsymbol{r}}}}\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial \mathit{\boldsymbol{x}}}} = \left[ {\begin{array}{*{20}{c}} {{x_r}}&{{x_s}}\\ {{y_r}}&{{y_s}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{r_x}}&{{r_y}}\\ {{s_x}}&{{s_y}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right] $ | (17) |
可知
| $ {r_x} = \frac{{{y_s}}}{J},{r_y} = - \frac{{{x_s}}}{J},{s_x} = - \frac{{{y_r}}}{J},{s_y} = \frac{{{x_r}}}{J} $ | (18) |
式中:J为雅克比行列式J=xrys-xsyr。而从方程式(16)可知
| $ \left( {{x_r},{y_r}} \right) = {\mathit{\boldsymbol{x}}_r} = \frac{{{\mathit{\boldsymbol{v}}^2} - {\mathit{\boldsymbol{v}}^1}}}{2},\left( {{x_s},{y_s}} \right) = {\mathit{\boldsymbol{x}}_s} = \frac{{{\mathit{\boldsymbol{v}}^3} - {\mathit{\boldsymbol{v}}^1}}}{2} $ | (19) |
通过上述关系式,可以在标准三角形单元内生成节点用以构造拉格朗日插值多项式,详细过程可见参考文献[12]。
最后,方程式(12)用NDG进行空间离散可得
| $ {\mathit{\boldsymbol{M}}^k}\frac{{{\rm{d}}\mathit{\boldsymbol{f}}_\alpha ^k}}{{{\rm{d}}t}} + \mathit{\boldsymbol{S}}_\alpha ^k\mathit{\boldsymbol{f}}_\alpha ^k = \mathit{\boldsymbol{R}}_\alpha ^k $ | (20) |
式中:fαk=[
| $ \begin{array}{*{20}{c}} {{{\left[ {{\mathit{\boldsymbol{M}}^k}} \right]}_{mn}} = \int_I {{\ell _m}\left( \mathit{\boldsymbol{r}} \right){\ell _n}\left( \mathit{\boldsymbol{r}} \right){J^k}{\rm{d}}\mathit{\boldsymbol{r}}} }\\ {m,n = 1, \cdots ,{N_p}} \end{array} $ | (21a) |
| $ \begin{array}{*{20}{c}} {{{\left[ {\mathit{\boldsymbol{S}}_\alpha ^k} \right]}_{mn}} = \int_I {{\mathit{\boldsymbol{e}}_\alpha } \cdot \frac{{\partial {\ell _m}\left( \mathit{\boldsymbol{r}} \right)}}{{\partial \mathit{\boldsymbol{r}}}}\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial \mathit{\boldsymbol{x}}}}{\ell _n}\left( \mathit{\boldsymbol{r}} \right){J^k}{\rm{d}}\mathit{\boldsymbol{r}}} }\\ {m,n = 1, \cdots ,{N_p}} \end{array} $ | (21b) |
| $ \begin{array}{*{20}{c}} {{{\left[ {\mathit{\boldsymbol{R}}_\alpha ^k} \right]}_{mn}} = }\\ {\int_{\partial \mathit{\boldsymbol{I}}} {\frac{1}{2}\left( {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{n}} - \left| {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{n}}} \right|} \right){{\left( {\hat f_\alpha ^ - - \hat f_\alpha ^ + } \right)}_m}{\ell _m}\left( \mathit{\boldsymbol{r}} \right){\ell _n}\left( \mathit{\boldsymbol{r}} \right)J_s^k{\rm{d}}\mathit{\boldsymbol{r}}} }\\ {m,n = 1, \cdots ,{N_p}} \end{array} $ | (21c) |
式中:Jk和Jsk分别为单元内部和单元边界的映射雅克比行列式,∂I为标准三角形I的边界。
1.3 龙格-库塔时间离散格式对于空间离散后的NDG方程式(20),可以进一步采用龙格-库塔格式进行时间离散。因此,先在方程两边乘以Mk的逆矩阵
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{f}}_\alpha ^k}}{{{\rm{d}}t}} = - {\mathit{\boldsymbol{M}}^{{k^{ - 1}}}}\mathit{\boldsymbol{S}}_\alpha ^k\mathit{\boldsymbol{f}}_\alpha ^k + {\mathit{\boldsymbol{M}}^{{k^{ - 1}}}}\mathit{\boldsymbol{R}}_\alpha ^k = {\cal L}\left( {\mathit{\boldsymbol{f}}_\alpha ^k} \right) $ | (22) |
应用四阶、五步龙格-库塔格式对式(22)进行时间离散
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}^{\left( 0 \right)}} = \mathit{\boldsymbol{f}}_\alpha ^{{k^{\left( n \right)}}}}\\ {j = 1, \cdots ,5:\left\{ \begin{array}{l} {\mathit{\boldsymbol{k}}^{\left( j \right)}} = {a_j}{\mathit{\boldsymbol{k}}^{\left( {j - 1} \right)}} + \delta t{\cal L}\left( {{\mathit{\boldsymbol{p}}^{\left( {j - 1} \right)}},} \right.\\ \;\;\;\;\;\;\;\;\left. {{t^{\left( n \right)}} + {c_j}\delta t} \right)\\ {\mathit{\boldsymbol{p}}^{\left( j \right)}} = {\mathit{\boldsymbol{p}}^{\left( {j - 1} \right)}} + {b_j}{\mathit{\boldsymbol{k}}^{\left( j \right)}} \end{array} \right.}\\ {\mathit{\boldsymbol{f}}_\alpha ^{{k^{\left( {n + 1} \right)}}} = {\mathit{\boldsymbol{p}}^{\left( 5 \right)}}} \end{array} $ | (23) |
式中:aj, bj和cj为给定的常数。关于四阶、五步龙格-库塔格式的更多细节可见参考文献[12]。
1.4 边界条件与传统的LBM一样,本文的NDG-LBM也需要根据边界条件来求解边界上未知的粒子分布函数(
进口/出口
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\hat f_\alpha ^ + = \hat f_\alpha ^ - }\\ {\hat f_\alpha ^ + = \hat f_\alpha ^{eq}\left( {{\rho _0},{\mathit{\boldsymbol{u}}_0}} \right)} \end{array}}&{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{n}} > 0}\\ {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{n}} > 0} \end{array}} \end{array} $ | (24a) |
固壁
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\hat f_\alpha ^ + = \hat f_\alpha ^ - }\\ {\hat f_\alpha ^ + = \hat f_{ - \alpha }^ - + 2{w_\alpha }{\rho _0}\left( {{\mathit{\boldsymbol{e}}_\alpha },{\mathit{\boldsymbol{u}}_0}} \right)/c_s^2} \end{array}}&{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{n}} > 0}\\ {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{n}} < 0} \end{array}} \end{array} $ | (24b) |
式中:ρ0和u0分别是边界上的密度和速度,
为了验证本文的NDG-LBM,首先模拟了不同雷诺数下的顶盖驱动方腔流。对于该问题,雷诺数定义为Re=UL/υ。其中,U为顶盖驱动速度,L为方腔的边长,υ为动力黏性系数计算区域用1 848个三角形单元进行离散,如图 2所示,插值多项式的阶数为N=3。

|
图 2 顶盖方腔驱动流的包含1 848个三角形单元的非结构网格 Figure 2 Unstructured mesh with 1 848 triangular elements for lid-driven cavity flow |
图 3给出了Re=100, 400, 1 000和5 000时的流线图。从图中可知,随着雷诺数的增加,主涡逐渐向方腔中心移动,左下角和右下角的两个次涡逐渐增大。当Re=5 000时,左上角还出现了第3个次涡,同时右下角出现了一个尺寸更小的涡。

|
图 3 顶盖方腔驱动流在Re=100,400,1 000和5 000时的流线图 Figure 3 Streamlines of lid-driven cavity flow at Re=100, 400, 1 000 and 5 000 |
为了验证本文NDG-LBM的准确性,图 4给出了Re=100和1 000时中线上的速度型并与Ghia等[14]的结果进行比较。图中,u, v为速度分量;x, y为中线坐标。从图中可知,本文的结果与文献中的结果符合得很好。特别地,当Re=1 000时采用MRT获得的结果相比于SRT更接近文献中的结果。这说明MRT能有效地确保高雷诺数流动模拟的准确性。

|
图 4 Re=100和1 000时中线上的速度型比较 Figure 4 Comparison of centerline velocity profiles at Re=100 and 1 000 |
2.2 静止单个圆柱绕流
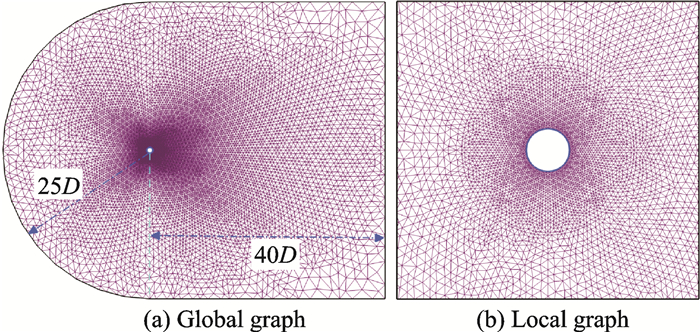
为了进一步验证NDG-LBM,本文还模拟了静止单个圆柱的绕流问题。对于此问题,雷诺数定义为Re=UD/υ。其中,U为自由来流速度,D为圆柱直径,υ为动力黏性系数。计算区域用2 944个三角形单元进行离散,如图 5所示,插值多项式的阶数仍取N=3。
|
图 5 静止单个圆柱绕流的包含2 944个三角形单元的非结构网格 Figure 5 Unstructured grids with 2 944 triangular elements for flowover stationary circular cylinder |
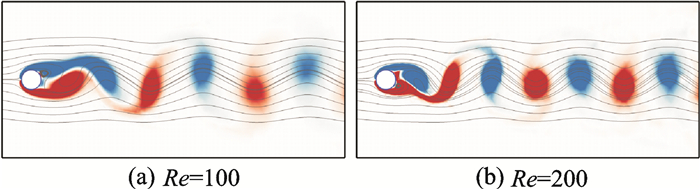
本文模拟了Re=100和200时的非定常流动。表 1给出了Re=100时的平均阻力系数Cd、最大升力幅值ΔCl和无量纲涡脱落频率St的计算结果,并与文献[15~17]中的结果进行了比较。由表 1可见,当前的计算结果与文献中的结果符合得很好。这再次证明了本文方法的可靠性。图 6给出了Re=100和200时流动达到周期性变化后的流线和瞬时涡量云图。从图中可以看到清晰的卡门涡街现象。
| 表 1 静止单个圆柱绕流在Re=100时的结果比较 Table 1 Comparison of results for flow over stationary circular cylinder at Re=100 |
|
图 6 静止单个圆柱绕流的流线和瞬时涡量云图 Figure 6 Streamlines and instantaneous vorticity contours for flow over stationary circular cylinder |
2.3 旋转-静止双圆柱绕流
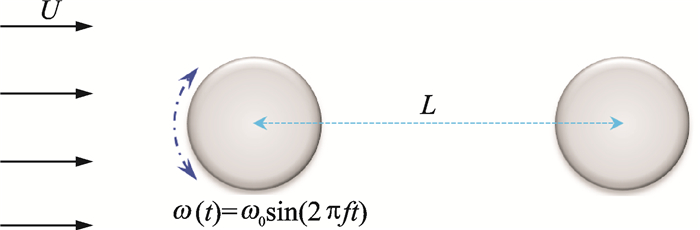
为了进一步检验NDG-LBM并展示其处理复杂问题的能力,本文还模拟了Re=150时双圆柱的绕流问题。其中两个圆柱前后放置,它们的大小一致(直径为D),它们之间的距离为L,同时前圆柱作旋转运动而后圆柱静止,如图 7所示。计算区域用3 962个三角形单元进行离散,区域大小与单圆柱问题一样。旋转圆柱的角速度变化为
|
图 7 旋转-静止圆柱绕流示意图 Figure 7 Sketch of flow over rotating-stationary circular cylinders |
| $ \omega \left( t \right) = {\omega _0}\sin \left( {2{\rm{ \mathit{ π} }}ft} \right) $ | (25) |
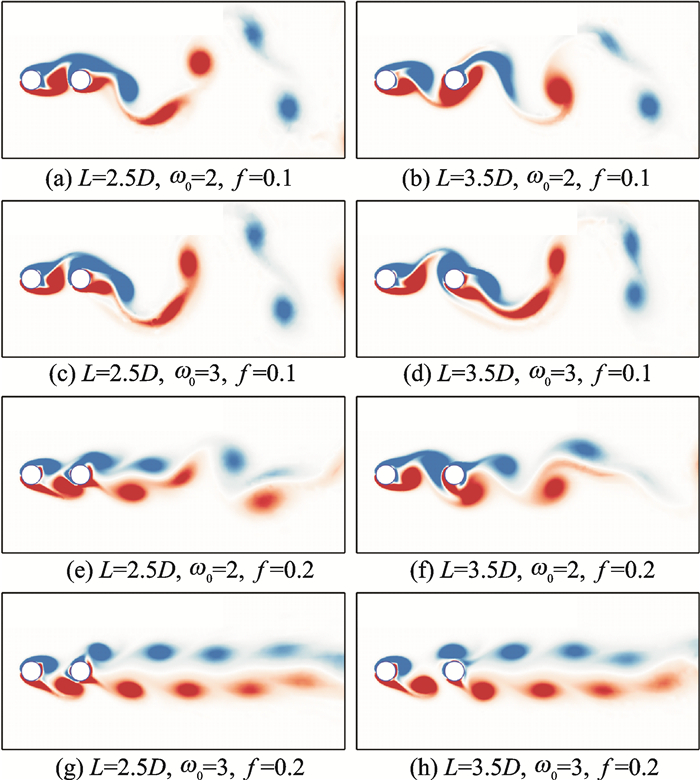
式中:ω0为角速度幅值,f为无量纲转动频率。在本文的模拟中,它们的取值分别为ω0=2,3和f=0.1,0.2。此外,圆柱之间的距离为L=2.5D和3.5D。
图 8给出了不同参数下的涡量云图。从图中可知,前圆柱的旋转运动显著地改变后圆柱的涡脱落过程。其中,圆柱之间的距离L和圆柱的转动频率f对后圆柱的涡脱落影响较小。然而,随着旋转幅度ω0的增大,后圆柱的涡脱落形态从交替分布逐渐转变成上下分布。
|
图 8 旋转-静止圆柱绕流的瞬时涡量云图 Figure 8 Instantaneous vorticity contours for flow over rotating-stationary circular cylinders |
2.4 NACA0012翼型绕流
为了进一步展示NDG-LBM处理高雷诺数问题的能力,本文还模拟了Re=5 000时NACA0012翼型的绕流问题,其中来流迎角为10°。
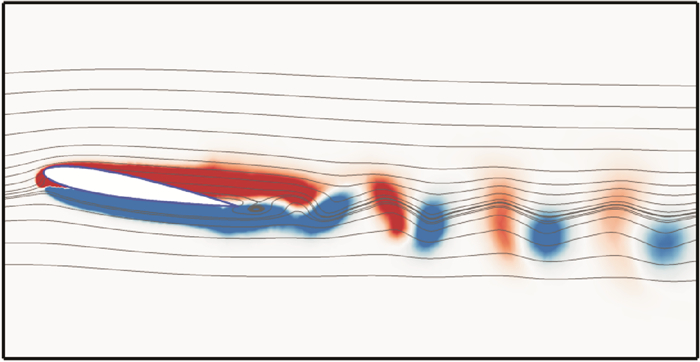
图 9给出了流动达到稳定以后的流线和涡量云图。从图中可知,翼型后缘的上表面附近存在回流区,同时流场中出现了典型的涡脱落现象。
|
图 9 NACA0012翼型绕流的流线和瞬时涡量云图 Figure 9 Streamlines and instantaneous vorticity contours for flow over NACA0012 airfoil |
3 结束语
本文基于节点间断有限元方法,提出了另一种求解格子波尔兹曼方程的方法,即NDG-LBM。该方法首先把LBE的碰撞过程和迁移过程拆成两步。其中碰撞过程用LBM中的多松弛时间模型进行求解,而迁移过程则还原成对流方程。然后采用NDG方法求解该对流方程,其中采用非结构网格进行空间离散,采用四阶、五步龙格-库塔格式进行时间离散。最后应用该方法模拟了顶盖方腔驱动流、静止单个圆柱绕流、旋转-静止双圆柱绕流以及高雷诺数NACA0012翼型绕流。计算所得的结果与文献中的结果很吻合,有效地验证了本文NDG-LBM的准确性和可靠性。
| [1] | AIDUN C K, CLAUSEN J R. Lattice-Boltzmann method for complex flows[J]. Annual Review of Fluid Mechanics, 2010, 42: 439–472. DOI:10.1146/annurev-fluid-121108-145519 |
| [2] | McNAMARA G R, ZANETTI G. Use of the Boltzmann equation to simulate lattice-gas automata[J]. Physical Review Letters, 1988, 61(20): 2332–2335. DOI:10.1103/PhysRevLett.61.2332 |
| [3] | HE X, LUO L S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation[J]. Physical Review E, 1997, 56(6): 6811–6817. DOI:10.1103/PhysRevE.56.6811 |
| [4] | ABE T. Derivation of the lattice Boltzmann method by means of the discrete ordinate method for the Boltzmann equation[J]. Journal of Computational Physics, 1997, 131(1): 241–246. DOI:10.1006/jcph.1996.5595 |
| [5] | MEI R, SHYY W. On the finite difference-based lattice Boltzmann method in curvilinear coordinates[J]. Journal of Computational Physics, 1998, 143(2): 426–448. DOI:10.1006/jcph.1998.5984 |
| [6] | XI H, PENG G, CHOU S H. Finite-volume lattice Boltzmann method[J]. Physical Review E, 1999, 59(5): 6202–6205. DOI:10.1103/PhysRevE.59.6202 |
| [7] | LEE T, LIN C L. A characteristic Galerkin method for discrete Boltzmann equation[J]. Journal of Computational Physics, 2001, 171(1): 336–356. DOI:10.1006/jcph.2001.6791 |
| [8] | COCKBURN B, SHU C W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems[J]. Journal of Scientific Computing, 2001, 16(3): 173–261. DOI:10.1023/A:1012873910884 |
| [9] | SHI X, LIN J, YU Z. Discontinuous Galerkin spectral element lattice Boltzmann method on triangular element[J]. International Journal for Numerical Methods in Fluids, 2003, 42(11): 1249–1261. DOI:10.1002/(ISSN)1097-0363 |
| [10] | DUSTER A, DEMKOWICZ L, RANK E. High-order finite elements applied to the discrete Boltzmann equation[J]. International Journal for Numerical Methods in Fluids, 2006, 67(8): 1094–1121. DOI:10.1002/(ISSN)1097-0207 |
| [11] | MIN M, LEE T. A spectral-element discontinuous Galerkin lattice Boltzmann method for nearly incompressible flows[J]. Journal of Computational Physics, 2011, 230(1): 245–259. DOI:10.1016/j.jcp.2010.09.024 |
| [12] | HESTHAVEN J S, WARBURTON T. Nodal discontinuous Galerkin methods: Algorithms, analysis, and applications[M]. New York: Springer-Verlag, 2008. |
| [13] | LALLEMAND P, LUO L S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability[J]. Physical Review E, 2000, 61(6): 6546–6562. DOI:10.1103/PhysRevE.61.6546 |
| [14] | GHIA U, GHIA K, SHIN C. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J]. Journal of Computational Physics, 1982, 48(3): 387–411. DOI:10.1016/0021-9991(82)90058-4 |
| [15] | GRESHO PM, CHAN ST, LEE RL, et al. A modified finite element method for solving the time-dependent, incompressible Navier-Stokes equations. Part 2: Applications[J]. International Journal for Numerical Methods in Fluids, 1984, 4(7): 619–640. DOI:10.1002/(ISSN)1097-0363 |
| [16] | KANG S. Characteristics of flow over two circular cylinders in a side-by-side arrangement at low Reynolds numbers[J]. Physics of Fluids, 2003, 15(9): 2486–2498. DOI:10.1063/1.1596412 |
| [17] | LAI M C, PESKIN C S. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity[J]. Journal of Computational Physics, 2000, 160(2): 705–719. DOI:10.1006/jcph.2000.6483 |
 2017, Vol. 49
2017, Vol. 49


