2. 南京航空航天大学自动化学院,南京,210016
2. College of Automation Engineering, Nanjing Unive rsity of Aeronautics & Astronau tics, Nanjing, 210016, China
随着航天事业的迅猛发展,不断提升运载能力、延长在轨时间以及提高机动性,已成为航天器设计的必然需求。液体燃料燃烧时既能释放充足能量,并且经济环保、易控制、能够长时间燃烧,在释放同样能量的情况下能比普通汽油减轻60%的自重,这对于航天器的飞行极为有利[1]。
为了满足更高难度的航天任务,航天器不可避免地携带大量的液体燃料和液态冷却剂,当液体燃料未充满时,自由液面将进行晃动、旋转、非规则拍振等运动,对刚体航天器产生显著的干扰力、干扰力矩和冲击压力[2], 致使航天器姿态不稳定,极有可能引发航天事故[3-5]。2010年2月,美国航空航天管理局发射的太阳动力学高精度观测卫星,其星载差错及纠错系统由于晃动共振发出过载警报,迫使观测器关闭主发动机并进入安全模式。
目前,液体晃动的研究方法主要有基于流体力学的数值模拟方法及实验方法[6]等。但由于势流理论分析得出的动力学模型较为复杂,不利于控制理论的应用,且适用情况限制较多,因此在工程中普遍用等效力学模型,如单摆、弹簧质量块的摆动替代复杂的流体运动,其等效的正确性已在相关著作及实验中进行了验证[7-8]。采用等效力学模型的充液航天器动力学建模方法主要有两种:文献[9]对系统进行了受力分析,将刚体球摆运动时产生的作用力、作用力与航天器执行器产生的推力、中心扭矩相结合,从而建立了系统整体动力学方程;文献[10]从充液航天器动能方程入手,通过求解Lagrange-Euler方程直接推导出了系统的动力学方程。目前,国内外充液航天器姿态控制方法大多应用在以上两种数学模型上,文献[11~12]在文献[9]建模基础上使用极点配置自校正控制策略实现了姿态角的镇定及跟踪;文献[13, 14~22]在文献[10]建模基础上分别采用分层滑模控制方法及Lyapunov稳定性原理设计了非线性反馈控制器。
目前,充液航天器的姿态控制方案大多是基于二维面内简化的充液航天器模型,而实际在轨运行的充液航天器所处环境为三维空间。目前针对充液航天器所处的三维空间的动力学建模文献较少,文献[23~24]针对三维空间内一类用质心面模型等效液体晃动的充液航天器,通过牛顿-欧拉法建立了动力学方程,但质心面模型缺少理论支持,在工程中的应用并不像单摆模型一样成熟和广泛,因此在本文中将对等效单摆模型的充液航天器进行三维空间上的动力学建模。
为了建立符合实际情况的充液航天器模型,本文对在轨匀速行驶的一类贮箱关于轴中心对称的三轴充液航天器进行了数学建模,推导得出了其动力学方程,并采用非线性滑模控制方法稳定了航天器机动姿态,具有一定的实际意义。
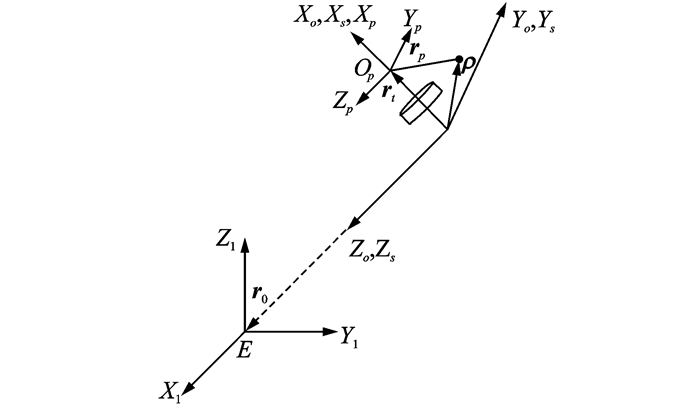
1 三轴充液航天器动力学建模 1.1 参考坐标系本节将介绍三轴充液航天器建模所使用的坐标参考系及航天器模型,如图 1所示。其中等效力学模型是根据液体晃动等效原则建立的一阶单摆模型,单摆摆动的动量、对航天器质心的动量矩都与液体运动相等效[25]。
|
图 1 充液航天器贮箱液体等效结构图及参考坐标系 Figure 1 Equivalent structure diagram and reference frame of spacecraft with liquid filled in tank |
图 1中:O为航天器质心,固体圆盘表示微重力情况下未晃动的液体质量;Op为单摆悬挂点;EX1Y1Z1为地心惯性坐标系;OX0Y0Z0为轨道坐标系;OXsYsZs为航天器体坐标系;OpXpYpZp为等效单摆坐标系;ms, mg, mp分别为刚体航天器、刚体等效圆盘及刚体等效单摆的质量。
由模型可知,地心指向航天器质心的矢量可定义为r0=(rox, roy, roz)
T,其中rox, roy, roz假定为航天器质心O点相对于地心惯性坐标系EX1Y1Z1的三轴坐标值;航天器质心距贮箱中心矢量定义为rt=(rt0, 0, 0)T,由于航天器燃料贮箱于航天器体坐标系轴Xs呈轴对称分布,因此假定rt0为等效晃动模型 (即单摆悬挂点) 距航天器质心的距离;单摆悬挂点指向单摆面矢量定义为
本文充液航天器动力学方程的求解采用Lagrange-Euler方法。首先由描述物体在力矩作用下运动规律的欧拉方程式可知[26],充液航天器对其质心的总惯性力矩为
| $ \begin{array}{l} T = \int_B {{\mathit{\boldsymbol{r}}_s} \times \mathit{\boldsymbol{a}}{\rm{d}}m} + \int_g {{\mathit{\boldsymbol{r}}_t} \times \mathit{\boldsymbol{a}}{\rm{d}}m} + \int_p {\mathit{\boldsymbol{\rho }} \times \mathit{\boldsymbol{a}}{\rm{d}}m} + \\ \;\;\;\;\;{m_p}\mathit{\boldsymbol{\rho }} \times {{\mathit{\boldsymbol{\ddot r}}}_d} \end{array} $ | (1) |
式中:a为加速度;ρ=rt+rp=(rt0+x, y, z);∫Brs×adm, ∫grt×adm, ∫pρ×adm分别为航天器质心指向单摆面的矢量以及刚体航天器、刚体等效圆盘及刚体等效单摆相对充液航天器质心的惯性力矩,这部分的惯性力矩由于具有相同的加速度,可得[26]
| $ \begin{array}{l} \int_B {{\mathit{\boldsymbol{r}}_s} \times \mathit{\boldsymbol{a}}{\rm{d}}m} + \int_g {{\mathit{\boldsymbol{r}}_t} \times \mathit{\boldsymbol{a}}{\rm{d}}m} + \int_p {\mathit{\boldsymbol{\rho }} \times \mathit{\boldsymbol{a}}{\rm{d}}m} = \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{J\dot \omega + \omega }} \times \mathit{\boldsymbol{J\omega }} \end{array} $ | (2) |
式中J=Js+Jg+Jp。为了简化方程,假设刚体航天器基矢坐标系与其惯性主轴方向重合。受航天器尺寸限制,指向刚体航天器及不晃动液体部分质量微元的矢量rs, rt为常矢量,因此Js+Jg为常正定对角矩阵
| $ {\mathit{\boldsymbol{J}}_s} + {\mathit{\boldsymbol{J}}_g} = \left[ {\begin{array}{*{20}{c}} {{J_1}}&{}&{}\\ {}&{{J_2}}&{}\\ {}&{}&{{J_3}} \end{array}} \right] $ | (3) |
Jp由于等效单摆的晃动,矢量ρ中有未知晃动位移,所以Jp可以由式 (4) 计算[27]
| $ {\mathit{\boldsymbol{J}}_p} = {m_p}\left( {\mathit{\boldsymbol{\rho }} \cdot \mathit{\boldsymbol{\rho I}} - \mathit{\boldsymbol{\rho }}{\mathit{\boldsymbol{\rho }}^{\rm{T}}}} \right) $ | (4) |
式中I为单位矩阵。将x1=rt0+x,ρ=(x1, y, z) 代入式 (4) 得
| $ {\mathit{\boldsymbol{J}}_p} = {m_p}\left[ {\begin{array}{*{20}{c}} {{y^2} + {z^2}}&{ - {x_1}y}&{ - {x_1}z}\\ { - {x_1}y}&{x_1^2 + {z^2}}&{ - yz}\\ { - {x_1}z}&{ - yz}&{x_1^2 + {y^2}} \end{array}} \right] $ | (5) |
式 (1) 中的
| $ \begin{array}{l} {{\mathit{\boldsymbol{\ddot r}}}_d} = {{\mathit{\boldsymbol{\ddot r}}}_0} + {{\mathit{\boldsymbol{\ddot r}}}_p} + {{\mathit{\boldsymbol{\ddot r}}}_t} + 2\mathit{\boldsymbol{\omega }} \times \left( {{{\mathit{\boldsymbol{\dot r}}}_t} + {{\mathit{\boldsymbol{\dot r}}}_p}} \right) + \\ \;\;\;\;\;\mathit{\boldsymbol{\dot \omega }}\left| {_S \times } \right.\left( {{\mathit{\boldsymbol{r}}_t} + {\mathit{\boldsymbol{r}}_p}} \right) + \mathit{\boldsymbol{\omega }} \times \left( {\mathit{\boldsymbol{\omega }} \times \left( {{\mathit{\boldsymbol{r}}_t} + {\mathit{\boldsymbol{r}}_p}} \right)} \right) \end{array} $ | (6) |
由于单摆悬挂点相对于充液航天器体坐标系静止,因此
| $ {{\mathit{\boldsymbol{\ddot r}}}_d} = {{\mathit{\boldsymbol{\ddot r}}}_0} + {{\mathit{\boldsymbol{\ddot r}}}_p} + 2\mathit{\boldsymbol{\omega }} \times \left( {{{\mathit{\boldsymbol{\dot r}}}_t} + {{\mathit{\boldsymbol{\dot r}}}_p}} \right) $ | (7) |
将式 (7) 代入
| $ \begin{array}{l} \mathit{\boldsymbol{\rho }} \times {{\mathit{\boldsymbol{\ddot r}}}_d} = \left( {y{{\ddot r}_{oz}} - z{{\ddot r}_{oy}} + y\ddot z - z\ddot y + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;2{\omega _x}y\dot y - 2{\omega _y}\dot xy - 2{\omega _z}\dot xz + \\ \;\;\;\;\;\;\;\;\;\;\;\left. {2{\omega _x}z\dot z} \right)\mathit{\boldsymbol{i + }}\left( {z{{\ddot r}_{ox}} - {x_1}{{\ddot r}_{oz}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;z\ddot x - {x_1}\ddot z + 22{\omega _y}z\dot z - 2{\omega _z}\dot yz - \\ \;\;\;\;\;\;\;\;\;\;\;\left. {2{\omega _x}{x_1}\dot y + 2{\omega _y}\dot x{x_1}} \right)\mathit{\boldsymbol{j + }}\left( {{x_1}{{\ddot r}_{oy}}} \right. - \\ \;\;\;\;\;\;\;\;\;\;\;y{{\ddot r}_{ox}} + {x_1}\ddot y - y\ddot x + 2{\omega _z}{x_1}\dot x - \\ \;\;\;\;\;\;\;\;\;\;\;\left. {2{\omega _x}{x_1}\dot z - 2{\omega _y}y\dot z + 2{\omega _x}y\dot y} \right)\mathit{\boldsymbol{k}} \end{array} $ | (8) |
结合式 (2,8),得姿态运动学方程式
| $ \mathit{\boldsymbol{T = J\dot \omega + \omega }} \times \mathit{\boldsymbol{J\omega + }}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{\ddot \eta + }}{\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{\dot \eta + }}{\mathit{\boldsymbol{A}}_3}\mathit{\boldsymbol{\eta + }}{\mathit{\boldsymbol{A}}_4} $ | (9) |
式中
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\eta }}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} y\\ z \end{array}} \right],\mathit{\boldsymbol{\omega = }}\left[ {\begin{array}{*{20}{c}} {{\omega _x}}\\ {{\omega _y}}\\ {{\omega _z}} \end{array}} \right],{\mathit{\boldsymbol{A}}_1} = {m_p}\left[ {\begin{array}{*{20}{c}} { - z}&y\\ 0&{ - {x_1}}\\ {{x_1}}&0 \end{array}} \right]}\\ {{\mathit{\boldsymbol{A}}_2} = {m_p}\left[ {\begin{array}{*{20}{c}} {2{\omega _x}y}&{2{\omega _x}z}\\ { - 2{\omega _z}z - 2{\omega _x}{x_1}}&{2{\omega _y}z}\\ {2{\omega _z}y}&{ - 2{\omega _x}{x_1} - 2{\omega _y}y} \end{array}} \right]}\\ {{\mathit{\boldsymbol{A}}_3} = {m_p}\left[ {\begin{array}{*{20}{c}} {{{\ddot r}_{oz}} - 2{\omega _y}\dot x}&{ - {{\ddot r}_{oy}} - 2{\omega _z}\dot x}\\ 0&{{{\ddot r}_{ox}} + \ddot x}\\ { - {{\ddot r}_{ox}} - \ddot x}&0 \end{array}} \right]}\\ {{\mathit{\boldsymbol{A}}_4} = {m_p}\left[ {\begin{array}{*{20}{c}} 0\\ { - {x_1}{{\ddot r}_{oy}} + 2{\omega _y}\dot x{x_1}}\\ {{x_1}{{\ddot r}_{oy}} + 2{\omega _z}\dot x{x_1}} \end{array}} \right]} \end{array} $ |
假设充液航天器在轨行驶,并没有变轨等机动行为,roz, roy方向加速度忽略不计,式 (9) 将简化为
| $ \mathit{\boldsymbol{J\dot \omega }} + {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{\ddot \eta = }} - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{J\omega }} - {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{\dot \eta + T}} $ | (10) |
系统动力学方程的推导还需要求解拉格朗日方程,该方程可从充液航天器动能方程中推导得出。充液航天器在轨飞行,以角速度ω相对轨道坐标系运动时,其总动能由平移动能和转动运动的动能一起组成,其动能方程如下
| $ E = \frac{1}{2}M\dot r_0^2 + \frac{1}{2}\mathit{\boldsymbol{\omega J\omega + }}\frac{1}{2}{m_p}\mathit{\boldsymbol{\dot r}}_d^2 $ | (11) |
式中:
| $ E = \frac{1}{2}M\dot r_0^2 + \frac{1}{2}\mathit{\omega }\mathit{\boldsymbol{J\omega + }}\frac{1}{2}{m_p}\left( {{f_1} + {f_2} + {f_3}} \right) $ | (12) |
式中
| $ \begin{array}{l} {f_1} = \dot r_{ox}^2 + {{\dot r}_{ox}}{{\dot x}_1} + 2{{\dot r}_{ox}}z{\omega _y} - 2{{\dot r}_{ox}}y{\omega _z} + \\ \;\;\;\;\;\;\dot x_1^2 + 2z{{\dot x}_1}{\omega _y} - 2y{{\dot x}_1}{\omega _z} + \omega _y^2{z^2} - \\ \;\;\;\;\;\;2{\omega _y}{\omega _z}yz + \omega _z^2{y^2} \end{array} $ | (13) |
| $ \begin{array}{l} {f_2} = \dot r_{oy}^2 + 2{{\dot r}_{oy}}\dot y + 2{{\dot r}_{oy}}{x_1}{\omega _z} - 2{{\dot r}_{oy}}z{\omega _x} + \\ \;\;\;\;\;\;\;{{\dot y}^2} + 2x\dot y{\omega _z} - 2z\dot y{\omega _x} + \omega _z^2x_1^2 - \\ \;\;\;\;\;\;\;2{\omega _x}{\omega _z}{x_1}z + \omega _x^2{z^2} \end{array} $ | (14) |
| $ \begin{array}{l} {f_3} = \dot r_{oz}^2 + 2{{\dot r}_{oz}}\dot z + 2{{\dot r}_{oz}}y{\omega _x} - 2{{\dot r}_{oz}}{x_1}{\omega _y} + \\ \;\;\;\;\;\;{{\dot z}^2} + 2y\dot z{\omega _x} - 2{x_1}\dot z{\omega _y} + \omega _x^2{y^2} - \\ \;\;\;\;\;\;2{\omega _y}{\omega _x}{x_1}y + \omega _y^2x_1^2 \end{array} $ | (15) |
同时考虑液体晃动阻尼方程R,根据参考文献[10]中的定义,假定该方程由Rayleigh损耗方程推导得出,表现了液体燃料晃动时产生的内部损耗,其形式为
| $ R = {\varepsilon _1}{{\dot y}^2} + {\varepsilon _2}{{\dot z}^2} $ |
式中ε1, ε2为保证内部损耗为正的系数,其值均大于零。由拉格朗日方程得出完整的充液航天器动力学方程,令L=E,有
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial \dot y}} - \frac{{\partial L}}{{\partial y}} + \frac{{\partial R}}{{\partial \dot y}} = 0\\ \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial \dot z}} - \frac{{\partial L}}{{\partial z}} + \frac{{\partial R}}{{\partial \dot z}} = 0 \end{array} $ | (16) |
将式 (12) 代入式 (16) 得
| $ {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{\dot \omega }} + \mathit{\boldsymbol{\ddot \eta }} = {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{\dot \eta }} + {\mathit{\boldsymbol{B}}_3}\mathit{\boldsymbol{\eta }} + {\mathit{\boldsymbol{B}}_4}\mathit{\boldsymbol{\omega }} $ | (17) |
式中
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} { - z}&0&{{x_1}}\\ y&{ - {x_1}}&0 \end{array}} \right],{\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} { - 2{r_1}}&{2{\omega _x}}\\ { - 2{\omega _x}}&{ - 2{r_2}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{B}}_3} = \left[ {\begin{array}{*{20}{c}} {\omega _x^2 + \omega _z^2}&{ - {\omega _y}{\omega _z}}\\ { - {\omega _y}{\omega _z}}&{\omega _x^2 + \omega _y^2} \end{array}} \right]}\\ {{\mathit{\boldsymbol{B}}_4} = \left[ {\begin{array}{*{20}{c}} 0&{ - l{\omega _x}}&{ - {{\dot r}_{ox}}}\\ 0&{{{\dot r}_{ox}}}&{ - l{\omega _x}} \end{array}} \right]} \end{array} $ |
综上所述,结合系统欧拉方程式 (10) 以及系统拉格朗日方程式 (17) 可得三轴充液航天器动力学方程
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J\dot \omega + }}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{\ddot \eta = }} - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{J\omega }} - {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{\dot \eta + T}}}\\ {{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{\dot \omega }} + \mathit{\boldsymbol{\ddot \eta }} = {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{\dot \eta }} + {\mathit{\boldsymbol{B}}_3}\mathit{\boldsymbol{\eta }} + {\mathit{\boldsymbol{B}}_4}\mathit{\boldsymbol{\omega }}} \end{array} $ | (18) |
三轴充液航天器系统是一类多输入多输出的非线性系统,其控制输入为作用在三轴上的力矩,液体燃料晃动状态为其内部状态,并不直接受三轴力矩控制。为了研究系统内部状态的性质,本节将采用文献[12]中的方法,分析系统的零动态特性。
首先,定义系统输出状态如下
| $ {y_1} = {\omega _x},{y_2} = {\omega _y},{y_3} = {\omega _z} $ | (19) |
系统各个状态变量定义如下
| $ \begin{array}{l} {x_1} = {\omega _x},{x_2} = {\omega _y},{x_3} = {\omega _z},{x_4} = y,{x_5} = \dot y\\ {x_6} = z,{x_7} = \dot z,{u_1} = {T_1},{u_2} = {T_2},{u_3} = {T_3} \end{array} $ |
对系统进行矩阵变换,将其化为状态方程形式,式 (17) 化为
| $ \mathit{\boldsymbol{\ddot \eta = }}{\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{\dot \eta + }}{\mathit{\boldsymbol{B}}_3}\mathit{\boldsymbol{\eta + }}{\mathit{\boldsymbol{B}}_4}\mathit{\boldsymbol{\omega + }}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{\dot \omega }} $ | (20) |
并代入式 (10) 得
| $ \begin{array}{l} \left( {\mathit{\boldsymbol{J}} - {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_1}} \right)\mathit{\boldsymbol{\dot \omega = }} - \mathit{\boldsymbol{\omega }} \times \left( {\mathit{\boldsymbol{J\omega }}} \right) - {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_4}\mathit{\boldsymbol{\omega }} - \\ \;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_2}} \right)\mathit{\boldsymbol{\dot \eta }} - {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_3}\mathit{\boldsymbol{\eta }} - {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_5} + \mathit{\boldsymbol{T}} \end{array} $ | (21) |
由上节知J=Js+Jg+Jp,令
| $ \mathit{\boldsymbol{J = }}\left[ {\begin{array}{*{20}{c}} {{J_1}}&{}&{}\\ {}&{{J_2}}&{}\\ {}&{}&{{J_3}} \end{array}} \right] $ |
结合式 (5) 可算得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}} - {A_1}{B_1} = {\mathit{\boldsymbol{J}}_s} + {\mathit{\boldsymbol{J}}_g} + \left( {{\mathit{\boldsymbol{J}}_p} - {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_1}} \right) = }\\ {{m_p}\left[ {\begin{array}{*{20}{c}} {{J_{11}}}&0&0\\ 0&{{J_{22}} - {z^2}}&{yz}\\ 0&{yz}&{{J_{33}} - {y^2}} \end{array}} \right]} \end{array} $ | (22) |
其行列式为
| $ \left| {\mathit{\boldsymbol{J}} - {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_1}} \right| = {J_{11}}{J_{22}}{J_{23}} + {J_{11}}{J_{33}}{z^2} + {J_{11}}{J_{22}}{y^2} $ | (23) |
式中
| $ {\left( {\mathit{\boldsymbol{J}} - {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{B}}_1}} \right)^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{M_1}}&0&0\\ 0&{{M_2}}&{{M_3}}\\ 0&{{M_3}}&{{M_4}} \end{array}} \right] $ | (24) |
式中
| $ \begin{array}{l} {M_1} = \frac{1}{{{J_{11}}}},{M_2} = \frac{{{J_{33}} + {y^2}}}{{{J_{22}}{J_{33}} + {J_{33}}{z^2} + {J_{22}}{y^2}}}\\ {M_3} = \frac{{yz}}{{{J_{22}}{J_{33}} + {J_{33}}{z^2} + {J_{22}}{y^2}}}\\ {M_4} = \frac{{{J_{22}} + {z^2}}}{{{J_{22}}{J_{23}} + {J_{33}}{z^2} + {J_{22}}{y^2}}} \end{array} $ |
由于液体晃动位移受贮箱尺寸限制,y, z为有界变量,由航天器刚体部分主惯性张量及液体晃动质量决定的J11, J22, J33在不考虑液体燃料消耗的情况下为常量 (考虑消耗时也为有界变量),因此Mi有界,设其界为
| $ \left| {{M_i}} \right| \le M_i^ * \;\;\;\;i = 1,2,3,4 $ | (25) |
将式 (24) 代入式 (21) 中即可求得 (即) 的状态方程。对系统输出状态进行求导
| $ \left\{ \begin{array}{l} {y_1} = {x_1}\\ {{\dot y}_1} = {{\dot x}_1} = {M_1}{f_a} + {M_1}{u_1}\\ {y_2} = {x_2}\\ {{\dot y}_2} = {{\dot x}_2} = {M_2}\left( {{f_b} + {u_2}} \right) + {M_3}\left( {{f_c} + {u_3}} \right)\\ {y_3} = {x_3}\\ {{\dot y}_3} = {{\dot x}_3} = {M_3}\left( {{f_b} + {u_2}} \right) + {M_4}\left( {{f_c} + {u_3}} \right) \end{array} \right. $ | (26) |
式中
| $ \begin{array}{l} {f_a} = \left( {{J_{22}} - {J_{33}}} \right){\omega _y}{\omega _z} + {m_p}\left( { - lz{\omega _x}{\omega _y}} \right. - \\ \;\;\;\;\;\;{{\dot r}_{ox}}y{\omega _y} - {{\dot r}_{ox}}z{\omega _z} + ly{\omega _x}{\omega _z} + \\ \;\;\;\;\;\;\left. {yz\omega _z^2 + {y^2}{\omega _y}{\omega _z} - {z^2}{\omega _y}{\omega _z} - yz\omega _y^2} \right)\\ {f_b} = \left( {{J_{33}} - {J_{11}}} \right){\omega _x}{\omega _z} + {m_p}\left( {{{\dot r}_{ox}}{x_1}{\omega _y} - } \right.\\ \;\;\;\;\;\;l{x_1}{\omega _x}{\omega _z} + 2\dot yz{\omega _z} - 2z\dot z{\omega _y} + \\ \;\;\;\;\;\;\left. {{x_1}z\omega _x^2 + {x_1}z\omega _y^2 - {x_1}y{\omega _y}{\omega _z}} \right)\\ {f_c} = \left( {{J_{11}} - {J_{22}}} \right){\omega _x}{\omega _y} + {m_p}\left( {{{\dot r}_{ox}}{x_1}{\omega _z} - } \right.\\ \;\;\;\;\;\;l{x_1}{\omega _x}{\omega _y} - 2\dot yy{\omega _z} + 2y\dot z{\omega _y} - \\ \;\;\;\;\;\;\left. {{x_1}y\omega _x^2 + {x_1}y\omega _z^2 - {x_1}z{\omega _y}{\omega _z}} \right) \end{array} $ |
由式 (26) 的求导可知,三轴充液航天器系统的相对阶为[r1=r2=r3=1]。之后将状态x限定在系统输出零子流形Z*上, 即
| $ {Z^ * } = \left\{ {\mathit{\boldsymbol{x}} \in {{\bf{R}}^7}\left| {{x_1} = {x_2} = {x_3} = 0} \right.} \right\} $ | (27) |
系统的零动态为
| $ \left\{ \begin{array}{l} {{\dot x}_4} = {f_{z1}}\left( x \right),{{\dot x}_5} = {f_{z2}}\left( x \right)\\ {{\dot x}_6} = {f_{z3}}\left( x \right),{{\dot x}_7} = {f_{z4}}\left( x \right) \end{array} \right. $ | (28) |
式中
| $ \begin{array}{l} {f_{z1}}\left( x \right) = {x_5}\\ {f_{z2}}\left( x \right) = {{\dot x}_1}{x_6} - \left( {l + {l_1}} \right){{\dot x}_3} + 2{x_1}{x_7} + \left( {x_1^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {x_3^2} \right){x_4} - {x_2}{x_3}{x_6} - l{x_1}{x_2} - {{\dot r}_{ox}}{x_3} - 2{\varepsilon _1}{x_5}\\ {f_{z3}}\left( x \right) = {x_7}\\ {f_{z4}}\left( x \right) = - {{\dot x}_1}{x_4} + \left( {l + {l_1}} \right){{\dot x}_2} - 2{x_1}{x_5} + \left( {x_1^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {x_2^2} \right){x_6} - {x_2}{x_3}{x_5} - l{x_1}{x_3} - {{\dot r}_{ox}}{x_2} - 2{\varepsilon _2}{x_7} \end{array} $ |
考虑液体晃动状态在平衡点x4=x5=x6=x7=0处的稳定性。求解雅可比矩阵Ja(x) 为
| $ {\mathit{\boldsymbol{J}}_a}\left( \mathit{\boldsymbol{x}} \right) = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {f_{z1}}}}{{\partial {x_4}}}}&{\frac{{\partial {f_{z1}}}}{{\partial {x_5}}}}&{\frac{{\partial {f_{z1}}}}{{\partial {x_6}}}}&{\frac{{\partial {f_{z1}}}}{{\partial {x_7}}}}\\ {\frac{{\partial {f_{z2}}}}{{\partial {x_4}}}}&{\frac{{\partial {f_{z2}}}}{{\partial {x_5}}}}&{\frac{{\partial {f_{z2}}}}{{\partial {x_6}}}}&{\frac{{\partial {f_{z2}}}}{{\partial {x_7}}}}\\ {\frac{{\partial {f_{z3}}}}{{\partial {x_4}}}}&{\frac{{\partial {f_{z3}}}}{{\partial {x_5}}}}&{\frac{{\partial {f_{z3}}}}{{\partial {x_6}}}}&{\frac{{\partial {f_{z3}}}}{{\partial {x_7}}}}\\ {\frac{{\partial {f_{z4}}}}{{\partial {x_4}}}}&{\frac{{\partial {f_{z4}}}}{{\partial {x_5}}}}&{\frac{{\partial {f_{z4}}}}{{\partial {x_5}}}}&{\frac{{\partial {f_{z4}}}}{{\partial {x_7}}}} \end{array}} \right] $ | (29) |
代入Rayleigh耗散方程阻尼系数ε1=0.0018, ε2=0.002得
| $ {\mathit{\boldsymbol{J}}_a}\left( \mathit{\boldsymbol{x}} \right) = \left[ {\begin{array}{*{20}{c}} 0&1&0&0\\ 0&{ - 0.0036}&0&0\\ 0&0&0&1\\ 0&0&0&{ - 0.004} \end{array}} \right] $ | (30) |
可以求得雅可比矩阵特征根为λ1, 2=0, λ3=-0.003 6, λ4=-0.004。根据线性系统理论分析可知,该系统因具有两个位于原点的特征值,其雅可比矩阵表现为奇异矩阵,在实际中存在参数不确定、外界干扰等情况时,临界稳定系统基本上属于不稳定的范畴。因此,三轴充液航天器为零动态不稳定系统。
2 滑模姿态控制器设计在该章节中,将在第1节推导的三轴充液航天器动力学方程以及四元数运动方程的基础上设计滑模姿态控制器,稳定充液航天器机动姿态。首先,给出四元数运动方程,该方程可以表示出刚体角位置及角速度,与欧拉运动学方程相比,不存在奇点问题[28]。
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\dot q}_0}} \\ {{{\dot q}_1}} \\ {{{\dot q}_2}} \\ {{{\dot q}_3}} \end{array}} \right] = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} { - {q_1}{\omega _x} - {q_3}{\omega _y} - {q_3}{\omega _z}} \\ {{q_0}{\omega _x} - {q_3}{\omega _y} + {q_2}{\omega _z}} \\ {{q_3}{\omega _x} + {q_0}{\omega _y} - {q_1}{\omega _z}} \\ { - {q_2}{\omega _x} + {q_1}{\omega _y} + {q_0}{\omega _z}} \end{array}} \right]} \\ {q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1} \end{array} $ | (31) |
参考第1节推导的系统状态方程,根据式 (26) 可得不存在外界干扰的旋转角加速度方程并根据该方程设计滑模控制器为
| $ \mathit{\boldsymbol{\dot \omega = }}\left[ {\begin{array}{*{20}{c}} {{M_1}{f_a} + {M_1}{T_1}} \\ {{M_2}\left( {{f_b} + {T_2}} \right) + {M_3}\left( {{f_c} + {T_3}} \right)} \\ {{M_3}\left( {{f_b} + {T_2}} \right) + {M_4}\left( {{f_c} + {T_3}} \right)} \end{array}} \right] $ | (32) |
结合式 (31,32),采用如式 (33) 所示的滑模控制器,当滑模面收敛到零时,角速度ω和四元数q都能收敛到零,表明三轴充液航天器可以在轨道坐标系上稳定机动行驶,此时体坐标系和轨道坐标系重合,航天器以加速度
| $ \left\{ \begin{gathered} {s_1} = {\omega _x} + {k_1}{q_1} \hfill \\ {s_2} = {\omega _y} + {k_2}{q_2} \hfill \\ {s_3} = {\omega _z} + {k_3}{q_3} \hfill \\ \end{gathered} \right. $ | (33) |
式中k1, k2, k3为保证滑模面渐近收敛的系数,值为正。对式 (33) 分别求导得
| $ \left\{ \begin{gathered} {{\dot s}_1} = {M_1}\left( {{f_a} + {T_1}} \right) + {k_1}{{\dot q}_1} \hfill \\ {{\dot s}_2} = {M_2}\left( {{f_b} + {T_2}} \right) + {M_3}\left( {{f_c} + {T_3}} \right) + {k_2}{{\dot q}_2} \hfill \\ {{\dot s}_3} = {M_3}\left( {{f_b} + {T_2}} \right) + {M_4}\left( {{f_c} + {T_3}} \right) + {k_3}{{\dot q}_3} \hfill \\ \end{gathered} \right. $ | (34) |
取kj, j=a, b, c为正数。通过选择控制输入T1, T2, T3,使其滑模面导函数为以下形式
| $ \left\{ \begin{gathered} {{\dot s}_1} = - {k_a}{\text{sign}}\left( {{s_1}} \right) \hfill \\ {{\dot s}_2} = - {k_b}{\text{sign}}\left( {{s_2}} \right) \hfill \\ {{\dot s}_3} = - {k_c}{\text{sign}}\left( {{s_3}} \right) \hfill \\ \end{gathered} \right. $ |
式中sign函数为符号函数,其作用为指出状态变量的正负号,即
| $ {\text{sign}}\left( x \right) = \left\{ \begin{gathered} 1\;\;\;\;\;\;x > 0 \hfill \\ 0\;\;\;\;\;x = 0 \hfill \\ - 1\;\;\;x < 0 \hfill \\ \end{gathered} \right. $ |
此时,滑模面满足渐近收敛充分条件[29]:
| $ \left\{ \begin{gathered} {T_1} = \frac{1}{{{M_1}}}\left( { - {k_a}{\text{sign}}\left( {{s_1}} \right) - {k_1}{{\dot q}_1}} \right) - {f_a} \hfill \\ {T_2} = \left( {{J_{22}} + {z^2}} \right)\left( { - {k_b}{\text{sign}}\left( {{s_2}} \right) - {k_2}{{\dot q}_2}} \right) - \hfill \\ \;\;\;\;\;\;yz\left( { - {k_c}{\text{sign}}\left( {{s_3}} \right) - {k_2}{{\dot q}_3}} \right) - {f_b} \hfill \\ {T_3} = - yz\left( { - {k_b}{\text{sign}}\left( {{s_2}} \right) - {k_2}{{\dot q}_2}} \right) + \left( {{J_{22}} + } \right. \hfill \\ \;\;\;\;\;\;\left. {{z^2}} \right)\left( { - {k_c}{\text{sign}}\left( {{s_3}} \right) - {k_3}{{\dot q}_3}} \right) - {f_c} \hfill \\ \end{gathered} \right. $ | (35) |
该控制器能保证不存在外界干扰的精确系统的姿态稳定,因为在控制器的作用下,滑模面及其变化率满足滑动稳定的条件,在该条件约束范围内,滑模面包含的状态变量ω, q都能逼近至零,因
此确保了充液航天器的姿态稳定。
为了验证滑模控制器抗干扰能力强的优势,在三轴充液航天器建模方程式 (18) 的基础上,考虑存在一定有界干扰d,并假设其界已知,为|di| < di*, i=1, 2, 3。系统模型为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J\dot \omega + }}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{\ddot \eta }} - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{J\omega }} - {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{\dot \eta + T + d}}} \\ {{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{\dot \omega }} + \mathit{\boldsymbol{\ddot \eta }} = {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{\dot \eta + }}{\mathit{\boldsymbol{B}}_3}\mathit{\boldsymbol{\eta + }}{\mathit{\boldsymbol{B}}_4}\mathit{\boldsymbol{\omega }}} \end{array} $ |
此时滑模面变化率方程变为如下形式
| $ \left\{ \begin{gathered} {{\dot s}_1} = {M_1}\left( {{f_a} + {T_1} + {d_1}} \right) + {k_1}{{\dot q}_1} \hfill \\ {{\dot s}_2} = {M_2}\left( {{f_b} + {T_2} + {d_2}} \right) + \hfill \\ \;\;\;\;\;\;{M_3}\left( {{f_c} + {T_3} + {d_3}} \right) + {k_2}{{\dot q}_2} \hfill \\ {{\dot s}_3} = {M_3}\left( {{f_b} + {T_2} + {d_2}} \right) + \hfill \\ \;\;\;\;\;\;{M_4}\left( {{f_c} + {T_3} + {d_3}} \right) + {k_3}{{\dot q}_3} \hfill \\ \end{gathered} \right. $ | (36) |
为了验证现在的滑模控制器依然可以保证系统状态稳定,设计如下形式的李雅谱诺夫函数,令
| $ {V_i} = \frac{1}{2}s_i^2\;\;\;i = 1,2,3 $ |
分别对其求导,并将所设计的滑模面相关方程式 (33,36) 代入,可以得到
| $ \begin{gathered} {{\dot V}_1} = {s_1}\left( {{M_1}{d_1} - {k_a}{\text{sign}}\left( {{s_1}} \right)} \right) \hfill \\ {{\dot V}_2} = {s_2}\left( {{M_2}{d_2} + {M_3}{d_3} - {k_b}{\text{sign}}\left( {{s_2}} \right)} \right) \hfill \\ {{\dot V}_3} = {s_3}\left( {{M_3}{d_2} + {M_4}{d_3} - {k_c}{s_3}{\text{sign}}\left( {{s_3}} \right)} \right) \hfill \\ \end{gathered} $ |
参考式 (25) 及干扰量的假定界,只要满足以下条件:ka>M1*d1*, kb>M2*d2*+M3*d3*, kc>M3*d2*+M4*d3*, 该滑模控制器即可满足李雅普诺夫稳定性原理。
在此条件下,
本节中,对三轴充液航天器系统进行仿真,验证建模及所设计的滑模姿态控制器的有效性。各参数、状态初值如下:mp=30kg, l=1.0m, rto=2.0m,
| $ {\mathit{\boldsymbol{J}}_s} + {\mathit{\boldsymbol{J}}_g} = \left[ {\begin{array}{*{20}{c}} {150}&{}&{} \\ {}&{180}&{} \\ {}&{}&{220} \end{array}} \right] $ |
干扰为
| $ \left[ {\begin{array}{*{20}{c}} {{d_1}} \\ {{d_2}} \\ {{d_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.25\sin \left( {0.2t} \right)} \\ {0.2\sin \left( {0.1t} \right)} \\ {0.3\sin \left( {0.3t} \right)} \end{array}} \right] $ |
同时,考虑充液航天器刚体部分转动惯量可能存在的不确定性,令
| $ \mathit{\boldsymbol{J}}_s^ * = {\mathit{\boldsymbol{J}}_s}\left( {1 + \Delta {\mathit{\boldsymbol{J}}_s}} \right),\mathit{\boldsymbol{J}}_g^ * = {\mathit{\boldsymbol{J}}_g}\left( {1 + \Delta {\mathit{\boldsymbol{J}}_g}} \right) $ |
式中
| $ \left| {\Delta {\mathit{\boldsymbol{J}}_s}} \right| \leqslant 100\% ,\left| {\Delta {\mathit{\boldsymbol{J}}_g}} \right| \leqslant 10\% $ |
|
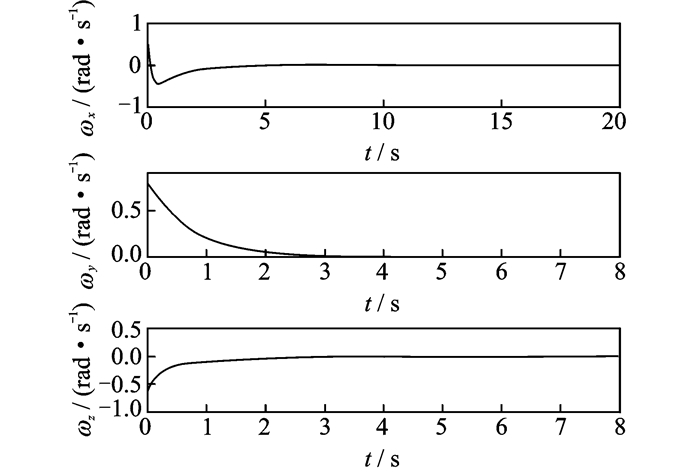
图 2 三轴充液航天器三轴角速度ωx, ωy, ωz Figure 2 Three-axis angular velocities ωx, ωy, ωz of three-axis liquid-filled spacecraft |
|
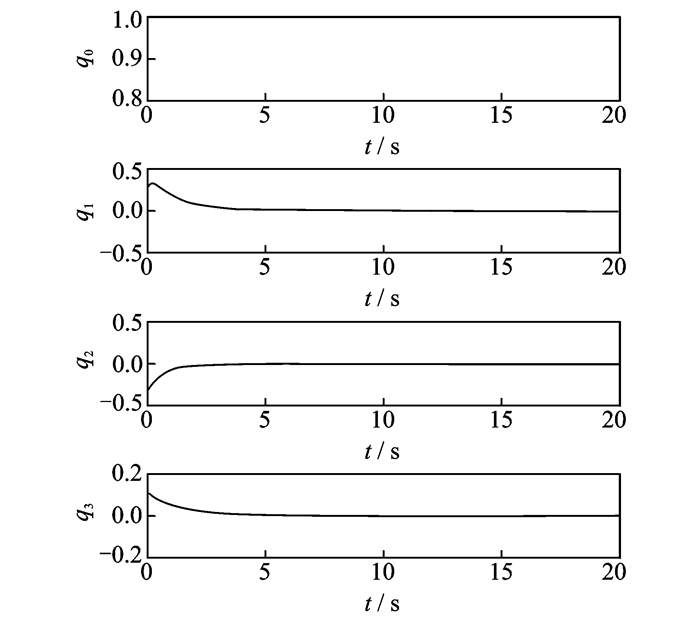
图 3 三轴充液航天器姿态四元数q0, q1, q2, q3 Figure 3 Attitude quaternions q0, q1, q2, q3 of three-axis liquid-filled spacecraft |
|
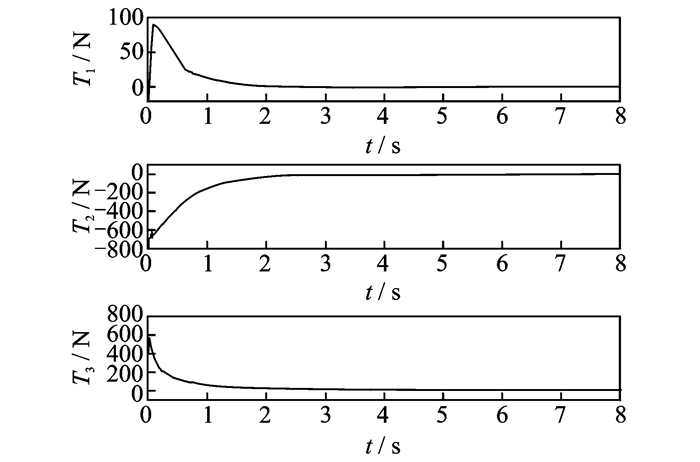
图 4 滑模姿态控制输入T1, T2, T3 Figure 4 Sliding mode attitude control inputs T1, T2, T3 |
|
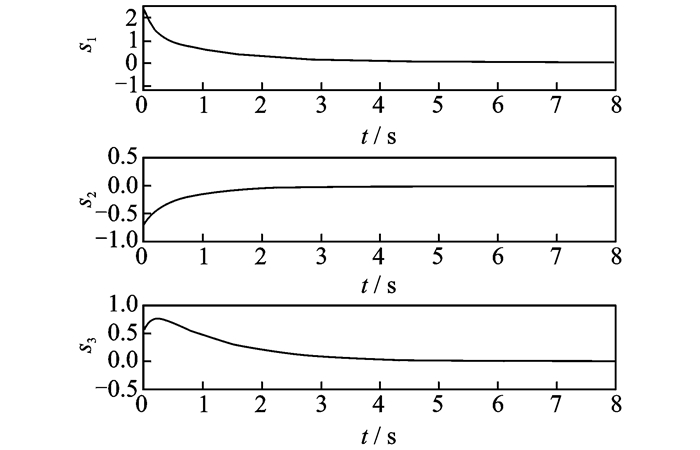
图 5 滑模面s1, s2, s3 Figure 5 Sliding surfaces s1, s2, s3 |
由图 2可见,三维平面上充液航天器体坐标系三轴方向上的角速度在滑模控制器的作用下快速渐近收敛;图 3所示欧拉角仿真结果表明,四元数方程满足q02+q12+q22+q32=1的稳定条件,图 2与图 3的仿真结果相结合可以保证三轴充液航天器在轨道坐标系上姿态稳定。图 4所描述的充液航天器三轴力矩及图 5描述的滑动平面曲线也进一步证明了控制器设计的有效性及可行性。由仿真结果可知,所设计的非线性滑模控制器可以应用于三轴充液航天器系统。并且,在系统参数存在一定不确定性及力矩干扰的情况下,该控制器仍然可以保证系统各状态的收敛,稳定航天器姿态,完成了控制目标。
4 结束语充液航天器是一个固-液耦合的系统,耦合的动力学特性是研究中的难点与热点。国内相关研究文献对三维空间内充液航天器数学建模及姿态稳定方面的研究较少,因此,为了针对充液航天器实际运行环境进行数学建模及姿态控制研究,本文对一类非线性、MIMO的三轴充液航天器,采用较为成熟的单摆模型等效液体燃料的小幅晃动,针对在轨运行的充液航天器选取了参考坐标系,运用欧拉、拉格朗日方程式对三轴充液航天器进行了数学建模,并在此基础上针对多变量复杂充液航天器系统设计了非线性滑模控制器,数值仿真的结果表明控制器能够在克服一定参数精度误差及干扰的情况下保证充液航天器在轨的稳定运行。
| [1] |
张芳謇.
火箭燃料[J]. 石油炼制与化工, 1958(2): 48–49.
ZHANG Fangjian. Rocket fuel[J]. Petroleum Processing and Petrochemicals, 1958(2): 48–49. |
| [2] |
尹立中, 王本利, 邹经湘.
航天器液体晃动与液固耦合动力学研究概述[J]. 哈尔滨工业大学学报, 1999, 31(2): 118–122.
YIN Lizhong, WANG Benli, ZOU Jingxiang. Introduction of liquid sloshing and liquid-solid coupled dynamics of spacecraft[J]. Journal of Harbin Institute of Technology, 1999, 31(2): 118–122. |
| [3] | QI Naiming, DONG Kai, WANG Xianlu, et al.Spacecraft propellant sloshing suppression using input shaping technique[C]//Computer Modeling and Simulation.Macau:International Conference on ICCMS, 2009:162-166. |
| [4] | GERRITS J.Dynamics of liquid-filled spacecraft:numerical simulation of coupled solid-liquid dynamics[D].Groningen:University of Groningen, 2001. |
| [5] |
岳宝增, 宋晓娟.
具有刚-柔-液-控耦合的航天器动力学研究进展[J]. 力学进展, 2013, 43(1): 162–172.
YUE Baozeng, SONG Xiaojuan. Advances in rigid-flexible-liquid control coupling dynamics of spacecraft[J]. Advances in Mechanics, 2013, 43(1): 162–172. |
| [6] |
李青, 王天舒, 马兴瑞.
充液航天器液体晃动和液固耦合动力学的研究与应用[J]. 力学进展, 2012, 42(4): 472–481.
LI Qing, WANG Tianshu, MA Xingrui. Reviews on liquid sloshing dynamics and liquid-structure coupling dynamics in liquid-filled spacecrafts[J]. Advances in Mechanics, 2012, 42(4): 472–481. |
| [7] | ABRAMSON H N.The dynamic behavior of liquids in moving containers[R].NASA SP-106, 1966. |
| [8] | CHU W H. Low-gravity fuel sloshing in an arbitrary axisymmetric rigid tank[J]. Transactions of the ASME, Journal of Applied Mechanics, 1970, 37(3): 828–837. DOI:10.1115/1.3408616 |
| [9] | SHAGEER H, TAO G.Modeling and adaptive control of spacecraft with fuel slosh:Overview and case studies[C]//AIAA Guidance, Navigation and Control Conference and Exhibit.Hilton Head, South Carolina:AIAA, 2007:1-19. |
| [10] | REYHANOGLU M. Modeling and control of space vehicles with fuel slosh dynamics[J]. Advances in Spacecraft Technologies, 2011, 24: 549–562. |
| [11] |
梁琼, 岳宝增, 于丹.
充液航天器目标跟踪自适应控制[J]. 空间控制技术与应用, 2011, 37(1): 40–44.
LIANG Qiong, YUE Baozeng, YU Dan. Adaptive control of target tracking for liquid-filled spacecraft[J]. Aerospace Control and Application, 2011, 37(1): 40–44. |
| [12] | SHAGEER H, TAO G.Zero dynamics analysis for spacecraft with fuel slosh[C]//AIAA Guidance, Navigation and control Conference and Exhibit.Honolulu, Hawaii:AIAA, 2008:1-18. |
| [13] |
邢健, 齐瑞云.
考虑燃料晃动效应的航天器自适应滑模姿态控制[J]. 空间控制技术与应用, 2013, 39(2): 20–25.
XING Jian, QI Ruiyun. Adaptive sliding-mode attitude control of spacecraft with fuel sloshing[J]. Aerospace Control and Application, 2013, 39(2): 20–25. |
| [14] | CHO S, MCCLAMROCH N H, REYHANOGLU M.Feedback control of a space vehicle with unactuated fuel slosh dynamics[C]//AIAA Guidance, Navigati on and control Conference and Exhibit.Denver, CO:AIAA, 2000:1-6. |
| [15] | Reyhanoglu M.Maneuvering control problems for a spacecraft with unactuated fuel slosh dynamics[C]//IEEE Control Applications.FL, USA:IEEE, 2003:695-699. |
| [16] | REYHANOGLU M, HERVAS J R.Nonlinear control of space vehicles with multi-mass fuel slosh dynamics[C]//IEEE 5th International Conference on Recent Advances in Space Technologies.Istanbul:IEEE, 2011:247-252. |
| [17] | REYHANOGLU M, HERVAS J R.Nonlinear control of a spacecraft with multiple fuel slosh modes[C]//IEEE 50th Conference on Decision and Control and European Control Conference.Orlando, FL, USA:IEEE, 2011:6192-6197. |
| [18] | REYHANOGLU M, HERVAS J R. Nonlinear dynamics and control of space vehicles with multiple fuels slosh modes[J]. Control Engineering Practice, 2012, 20(9): 912–918. DOI:10.1016/j.conengprac.2012.05.011 |
| [19] | HERVAS J R, REYHANOGLU M.Control of a spacecraft with time-varying propellant slosh parameters[C]//12th International Conference on Control, Automation and Systems.Korea:IEEE, 2012:1621-1626. |
| [20] |
顾黄兴.充液航天器液体晃动抑制控制研究[D].南京:南京航空航天大学, 2014.
GU Huangxing.Research on attitude control of spacecraft with fuel slosh[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2014. |
| [21] |
顾黄兴, 齐瑞云.一类充液航天器的非线性自适应反馈控制[C]//第三十二届中国控制会议论文集 (A卷).西安:[s.n.], 2013.
GU Huangxing, QI Ruiyun.Nonlinear adaptive feedback control of a kind of liquid-filled spacecraft[C]//The 32nd Chinese Control Conference.Xi′an, China:[s.n.], 2013. |
| [22] |
顾黄兴, 齐瑞云.
带液体晃动航天器的非线性自适应反馈控制[J]. 航天控制, 2013, 31(4): 72–77.
GU Huangxing, QI Ruiyun. Nonlinear adaptive feedback controller for spacecraft with fuel slosh[J]. Aerospace Control, 2013, 31(4): 72–77. |
| [23] |
黄华, 周志成, 杨雷, 等.
充液航天器大幅晃动耦合动力学建模仿真研究[J]. 航天器工程, 2009, 18(5): 37–41.
HUANG Hua, ZHOU Zhichen, YANG Lei, et al. Coupled dynamic modeling and simulation for spacecraft with large amplitude liquid sloshing[J]. Space craft Engineering, 2009, 18(5): 37–41. |
| [24] |
黄华, 杨雷, 张熇, 等.
航天器贮箱大幅液体晃动三维质心面等效模型研究[J]. 宇航学报, 2010, 31(1): 55–59.
HUANG Hua, YANG Lei, ZHANG He, et al. Research on 3D constraint surface model for large amplitude liquid sloshing on spacecraft tank[J]. Journal of Astronautics, 2010, 31(1): 55–59. |
| [25] |
刘延柱.
航天器姿态动力学[M]. 北京: 国防工业出版社, 1995: 330-336.
LIU Yanzhu. Spacecraft attitude dynamics[M]. Beijing: National De fence Industry Press, 1995: 330-336. |
| [26] |
刘暾, 赵钧.
空间飞行器动力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003: 163-166.
LIU Tun, ZHAO Jun. Modern spacecraft dynamics[M]. Harbin: Harbin Institute of Technology Press, 2003: 163-166. |
| [27] |
BATE R R.航天动力学基础[M].吴鹤鸣, 李肇杰, 译.北京:北京航空航天大学出版社, 1990:73-76.
BATE R R.Fundamentals of astrodynamics[M].WU Heming, LI Zhaojie, Tran.Beijing:Beihang University Press, 1990:73-76. |
| [28] |
黄圳圭.
航天器姿态动力学[M]. 长沙: 国防科技大学出版社, 1997: 252-255.
HUANG Zhengui. Spacecraft attitude dynamics[M]. Changsha: National University of Defense Technology Press, 1997: 252-255. |
| [29] | XU Haojian, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of Guidance Control and Dynamics, 2004, 27(5): 835–836. |
 2017, Vol. 49
2017, Vol. 49


