2. 南京航空航天大学民航学院, 南京, 210016;
3. 江苏理工学院商学院, 常州, 213000
2. College of Civil Aviation, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China;
3. School of Business, Jiangsu University of Technology, Changzhou, 213000, China
随着飞行流量的加大,空域资源利用日趋紧张。在交通流态势复杂区域,基于初始飞行计划并结合主观经验的交通流调控方式不能有效适应空域高密度运行的需要,由此提出了基于航迹的航空器运行方式,该类运行方式以时空形式对航空器在空域内运行时各位置点的时空参数进行精确描述,并通过改变航空器通过某特定位置点的时刻来避免飞行冲突。在交通流密集的复杂空域应用基于航迹的航空器运行方式可以有效应对大流量和小间隔条件下的航空器流组织情形[1]。针对基于航迹运行的航空器流组织形式,它在战略层面上需要获取单一航空器的初始运行轨迹并由此对特定的航空器流实施初始调配。在战略运行轨迹推算方面,Lygeros等应用航空器历史运行数据挖掘方法和航空器动力学性能模型演算方法获取初始起飞爬升阶段的轨迹数值[2]。马博敏等为获取航空器经过航路上关键位置点的时刻,基于矩形框算法对航空器轨迹进行推算[3]。刘恒泽等应用交互式多模型算法获取了航空器的外推轨迹[4]。韩云祥等提出了一种模块化的战略航迹演化通用模型,并构建了相应的宏观和微观Petri网演化模型[5]。Laith等基于机载雷达传感器数据,提出了一种智能估计算法来确定航空器的运行状态演化过程,从而为冲突探测提供可靠依据[6]。Yong等应用航空器飞行计划数据和实时气象数据,结合航空器动力学性能模型推测得到了航空器4D轨迹[7]。Sungkwon等通过融入概率信息和轨迹模式,提出了一种预测航空器到达时间的分析框架[8]。Juan等将航空器轨迹信息进行了层次划分,基于不同层级间和同一层级内的信息交互,应用和飞行意图相关的正则语言集获取航空器轨迹信息[9]。David等基于航空器实时轨迹数据,提出了一种自适应轨迹预测算法来提高爬升阶段航空器轨迹预测结果的准确性[10]。Kairat等在应用小波变换理论对历史轨迹数据进行处理的基础上,基于局部线性函数回归方法对航空器运行轨迹进行了推测[11-12]。以单航空器战略航迹和实时航迹推测为基础,针对多航空器航迹规划问题,已有研究探讨的问题主要与飞行冲突解脱相关,从战术层面对多航空器解脱轨迹进行规划,主要包括混合整数规划方案和最优控制方案等类型[13-15]。针对地面交通系统规划问题,Goverde等基于极大代数理论对建模过程以及系统内在演化的周期性、稳定性和鲁棒性等特征进行了详细阐述[16]。Schutter等基于双子代数模型和鲁棒控制理论对列车的运行组织优化方案进行了讨论[17-18]。
总体来看,相关文献并没有在战略层面给出多航空器无冲突航迹生产的方案,从而导致单条航迹推测结果不理想。此外,战略层面多航空器航迹规划过程所涉及到的约束条件存在严重的逻辑非线性特征且各种随机因素都会影响到航迹规划结果,这对于直接研究各航空器的航迹规划过程造成了很大困难。本文在极大代数理论框架下,通过将航空器流视为不同的批次,针对战略层面的多航空器航迹鲁棒规划问题进行优化建模。
1 单航段航空器轨迹规划代数模型国外学者Cuninghame-Green从对离散事件问题的研究中抽象出了极大代数理论并指明了其重要的应用前景,Cohen及其合作者将该理论成功应用于与离散事件动态相关的多个场合,本文首先给出其中几类基本的运算法则[19]:
(1) 令R表示整个实数域,符号“-∞”表示负无穷,那么可将其定义域设定为:R=R∪{-∞};
(2) 若a, b∈R表示两个标量,那么可将符号⊕和⊗定义为“取大”算子和“取和”算子,即
| $ a \oplus b = \max \left( {a,b} \right),a \otimes b = a + b $ |
(3) 设A∈ Rm×n和B∈Rm×n为任意两个矩阵,则定义⊕运算为
| $ {\left( {\mathit{\boldsymbol{A}} \oplus \mathit{\boldsymbol{B}}} \right)_{ij}} = {\left( \mathit{\boldsymbol{A}} \right)_{ij}} \oplus {\left( \mathit{\boldsymbol{B}} \right)_{ij}} = \max \left\{ {{{\left( \mathit{\boldsymbol{A}} \right)}_{ij}},{{\left( \mathit{\boldsymbol{B}} \right)}_{ij}}} \right\} $ |
设A∈Rm×r和B∈Rr×n为任意两个矩阵,则定义⊗运算为
| $ \begin{array}{*{20}{c}} {{{\left( {\mathit{\boldsymbol{A}} \oplus \mathit{\boldsymbol{B}}} \right)}_{ij}} = \sum\limits_{l = 1}^r {_ \oplus \left\{ {{{\left( \mathit{\boldsymbol{A}} \right)}_{ij}} \otimes {{\left( \mathit{\boldsymbol{B}} \right)}_{ij}}} \right\}} = }\\ {\mathop {\max }\limits_{1 \le l \le r} \left\{ {{{\left( \mathit{\boldsymbol{A}} \right)}_{ij}} + {{\left( \mathit{\boldsymbol{B}} \right)}_{ij}}} \right\}} \end{array} $ |
(4) 零元ε定义为“负无穷大”,单位元e定义为“零”。
如图 1所示,本文以在航段AB上运行的航空器流为基础,着重探讨空中交通系统的状态演化过程及其模型构建问题。针对单一航段,空中交通系统的演化可用n个子段M1, M2, …, Mn对m架航空器P1, P2, …, Pm所提供的服务状态来表征,令各子航段的长度均为最小水平间隔dmin。基于初始飞行计划,Pi(i=1, 2, …, m) 要接受n个子段M1, M2, …, Mn所提供的服务且各子段Mj(j=1, 2, …, n) 均要对m架航空器P1, P2, …, Pm提供服务。在系统运行过程中,将各子段对各个航空器所提供的服务称为“服务活动”,并称航空器进入某子段或某子段开始提供服务为系统资源输入,航空器离开某子段或某子段服务完成为系统资源输出,因此该服务过程中共含有mn个服务活动且系统资源输入和输出的数目均为 (m+n)。本文在对各类系统变量及参数进行定义的基础上,获取系统演化的“状态方程”和“输出方程”[18, 20, 21]。
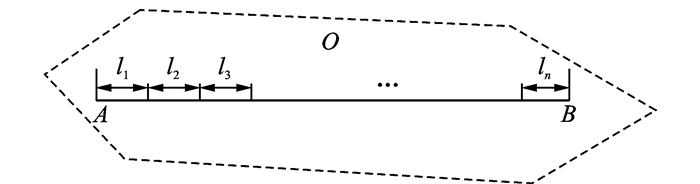
|
图 1 单一子航段划分 Figure 1 Division of single segment |
本文定义u(k) 为输入变量,且u(k) 表示相对于一个批次服务过程中,第k架航空器到达参考区域中初始航段l1入口的时间;定义xi(k) 为状态变量,且xi(k) 表示区域O中航段li对第k架航空器开始提供服务的最早时间,其中i=1, 2, …, m;定义y(k) 为输出变量,y(k) 表示相对于一个批次服务过程中,第k架航空器离开参考区域O的时间;定义ti(k) 为服务时间,且ti(k) 表示相对于一个批次服务过程中,第k架航空器在参考区域O中航段i上运行的时间,其中i=1, 2, …, m;定义tk为缓冲时间,且tk表示相对于一个批次服务过程中,第k架航空器在参考区域O中以最小速度vk, min运行距离dmin所需的时间。
在构建系统的代数模型时,需要首先设定系统服务过程所需满足的各类逻辑规则。对于空中交通系统运行过程,通过融入缓冲时间因子,Mj对Pi的服务得以开始,当且仅当“Mj(j=1, 2, …, n) 可用”和“Pi(i=1, 2, …, m) 处于子段入口”这两个条件同时满足,其中i=1, 2, …, m;j=1, 2, …, n。按照“先到先服务”原则,在考虑航空器间的间隔是最小安全间隔的前提下,依此服务条件可知该服务过程应遵循的各类规则为:
规则1 i=1和j=1时,服务条件对应于“航段j可利用且航空器i处于该航段入口”;
规则2 i=1和j≠1时,服务条件对应于“航段 (j-1) 对航空器i服务结束且航段j可用”;
规则3 i≠1和j=1时,服务条件对应于“航段j对航空器 (i-1) 服务结束且航空器i处于子段入口”;
规则4 i≠1和j≠1时,服务条件对应于“航段j对航空器 (i-1) 服务结束且航段(j-1)对航空器i服务结束”。
对所讨论的串行服务过程,基于上述各类规则可得到空中交通系统的状态方程为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_1}\left( k \right) = \max \left( {{\mathit{\boldsymbol{x}}_1}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_1}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_k},\mathit{\boldsymbol{u}}\left( k \right)} \right)\\ {\mathit{\boldsymbol{x}}_2}\left( k \right) = \max \left( {{\mathit{\boldsymbol{x}}_1}\left( k \right) + {\mathit{\boldsymbol{t}}_1}\left( k \right),{\mathit{\boldsymbol{x}}_2}\left( {k - 1} \right)} \right. + \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{t}}_2}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_k}} \right)\\ {\mathit{\boldsymbol{x}}_3}\left( k \right) = \max \left( {{\mathit{\boldsymbol{x}}_2}\left( k \right) + {\mathit{\boldsymbol{t}}_2}\left( k \right),{\mathit{\boldsymbol{x}}_3}\left( {k - 1} \right)} \right. + \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{t}}_3}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_k}} \right)\\ \vdots \\ {\mathit{\boldsymbol{x}}_{m - 2}}\left( k \right) = \max \left( {{\mathit{\boldsymbol{x}}_{m - 3}}\left( k \right) + {\mathit{\boldsymbol{t}}_{m - 3}}\left( k \right)} \right.,\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{x}}_{m - 2}}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_{m - 2}}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_k}} \right)\\ {\mathit{\boldsymbol{x}}_{m - 1}}\left( k \right) = \max \left( {{\mathit{\boldsymbol{x}}_{m - 2}}\left( k \right) + {\mathit{\boldsymbol{t}}_{m - 2}}\left( k \right)} \right.,\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{x}}_{m - 1}}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_{m - 1}}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_k}} \right)\\ {\mathit{\boldsymbol{x}}_m}\left( k \right) = \max \left( {{\mathit{\boldsymbol{x}}_{m - 1}}\left( k \right) + {\mathit{\boldsymbol{t}}_{m - 1}}\left( k \right)} \right.,\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{x}}_m}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_m}\left( {k - 1} \right) + {\mathit{\boldsymbol{t}}_k}} \right) \end{array} \right. $ | (1) |
输出方程为
| $ \mathit{\boldsymbol{y}}\left( k \right) = {\mathit{\boldsymbol{x}}_m}\left( k \right) + {\mathit{\boldsymbol{t}}_m}\left( k \right) $ | (2) |
针对式 (1, 2) 中的各类系统变量,通过进一步扩展,若引入状态向量x(k)=[x1(k), x2(k), …, xm(k)]T,输入向量u(k) 和输出向量y(k),那么其状态方程为和输出方程分别为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( k \right) = \mathit{\boldsymbol{A}}\left( k \right) \otimes \mathit{\boldsymbol{x}}\left( {k - 1} \right) \oplus \mathit{\boldsymbol{B}}\left( k \right) \otimes \mathit{\boldsymbol{u}}\left( k \right)\\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{C}}\left( k \right) \otimes \mathit{\boldsymbol{x}}\left( k \right) \end{array} \right. $ | (3) |
根据前文的论述,针对航空器流控制模型,可以得到以下几点结论:
(1) 模型表征了系统服务过程中状态、输入和输出等各类变量间的“线性”因果关系。
(2) 模型对系统参数具有相对固定性,针对特定的航路空间布局,当航空器进入次序变化时,模型所改变的仅是系数矩阵的数值而非模型相对形式。
(3) 在考虑各种随机因素时,模型中的参数ti(k) 属于随机量,系统状态量也属于随机量,由此将其扩展为随机形式。
(4) 对于所构建的航路-航空器系统极大代数模型,若进一步地给定初始状态向量x(0) 和输入变量u(l)(l=1, 2, …, k),那么可得到系统状态变量和输出变量的迭代过程为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( k \right) = {\mathit{\boldsymbol{A}}^{{ \otimes ^k}}} \otimes \mathit{\boldsymbol{x}}\left( 0 \right) \otimes \sum\limits_{l = 1}^k {_ \oplus {\mathit{\boldsymbol{A}}^{{ \otimes ^{k - 1}}}} \otimes \mathit{\boldsymbol{B}} \otimes \mathit{\boldsymbol{u}}\left( l \right)} \\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{C}} \otimes {\mathit{\boldsymbol{A}}^{{ \otimes ^k}}} \otimes \mathit{\boldsymbol{x}}\left( 0 \right) \oplus \sum\limits_{l = 1}^k {_ \oplus \mathit{\boldsymbol{C}} \otimes } \\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{A}}^{{ \otimes ^{k - 1}}}} \otimes \mathit{\boldsymbol{B}} \otimes \mathit{\boldsymbol{u}}\left( l \right) \end{array} \right. $ | (4) |
式中:A⊗k表示极大代数意义下k个矩阵A的乘积,即⊗;
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{t_1}\left( {k - 1} \right) + {t_k}}& \cdots & \cdots & \cdots &\varepsilon \\ {{t_1}\left( {k - 1} \right) + {t_k} + {t_1}\left( k \right)}&{{t_2}\left( {k - 1} \right) + {t_k}}& \cdots & \cdots &\varepsilon \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {{t_1}\left( {k - 1} \right) + {t_k}\sum\limits_{p = 1}^{m - 2} {{t_p}\left( k \right)} }&{{t_2}\left( {k - 1} \right) + {t_k}\sum\limits_{q = 2}^{m - 2} {{t_q}\left( k \right)} }& \cdots &{{t_{m - 1}}\left( {k - 1} \right) + {t_k}}& \vdots \\ {{t_1}\left( {k - 1} \right) + {t_k}\sum\limits_{p' = 1}^{m - 1} {{t_{p'}}\left( k \right)} }&{{t_2}\left( {k - 1} \right) + {t_k}\sum\limits_{q' = 2}^{m - 1} {{t_{q'}}\left( k \right)} }& \cdots & \cdots &{{t_m}\left( {k - 1} \right) + {t_k}} \end{array}} \right]}\\ {\mathit{\boldsymbol{B}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} 0\\ {{t_1}\left( k \right)}\\ {{t_1}\left( k \right) + {t_2}\left( k \right)}\\ \vdots \\ {{t_1}\left( k \right) + {t_2}\left( k \right) + \cdots + {t_{m - 1}}\left( k \right)} \end{array}} \right]\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{C}}\left( k \right) = {{\left[ {\begin{array}{*{20}{c}} \varepsilon \\ \varepsilon \\ \varepsilon \\ \vdots \\ {{t_m}\left( k \right)} \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
以上讨论的是单一航段上空中交通系统状态演化模型的构建方法,下文着重讨论交叉航段上空中交通系统状态演化模型的构建。如图 2所示,以典型的交叉航段为例,设定|C2D1|=|C1D2|=|E1F2|=|E2F1|=|dmin|。在交叉航段内,可将各个冲突位置点归结为航段交叉点附近的各分段点。若经过交叉口O的前后两航空器和的运行轨迹相同,那么此种状况类似于单一航段情形。
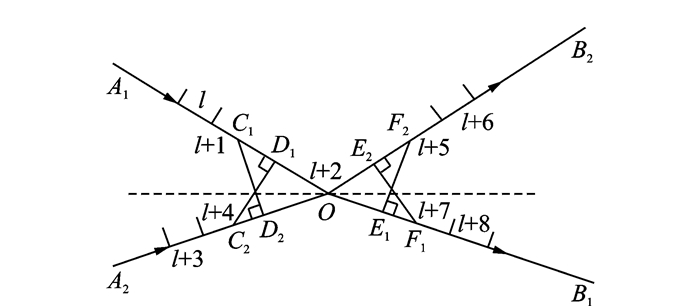
|
图 2 交叉子航段划分 Figure 2 Division of crossover segment |
不失一般性,对于A1OB1上的航空器g和在A2OB2上的航空器,若g先到达交叉点O,按照先到先服务原则,在A1OB1和A2OB2上两航空器需满足的约束条件同上。此外,在O处还需满足
| $ \begin{array}{*{20}{c}} {{x_{l + 2}}\left( h \right) = \max \left( {{x_{l + 4}}\left( h \right) + {t_{l + 4}}\left( h \right)} \right.,}\\ {\left. {{x_{l + 2}}\left( g \right) + {t_{l + 2}}\left( g \right) + {t_h}} \right)} \end{array} $ | (5) |
在航空器实际运行中,一个基本空域单元内可能存在各种各样的飞行冲突。因此可以前文所构建单航段空中交通系统代数模型为基础,建立空域单元的极大代数合成模型。基于以上讨论,可将空域单元的合成模型视为由单个基本模型串联的组合,不妨设第 (i-1) 个系统模型Σi-1(Ai-1, B i-1, Ci-1) 与第个冲突控制模型Σi(Ai, Bi, Ci) 为如图 3所示的串联关系。
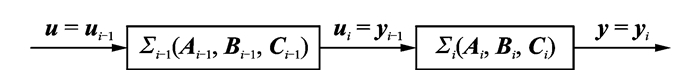
|
图 3 子模型串联结构 Figure 3 Series connection of sub-models |
运用向量-矩阵表示方法可得合成后系统的状态方程和输出方程分别为
| $ \begin{array}{*{20}{c}} {\left[ \begin{array}{l} {\mathit{\boldsymbol{x}}_{i - 1}}\left( k \right)\\ {\mathit{\boldsymbol{x}}_i}\left( k \right) \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{i - 1}}}&{\bf{0}}\\ {{\mathit{\boldsymbol{B}}_i} \otimes {\mathit{\boldsymbol{C}}_{i - 1}}}&{ \otimes {\mathit{\boldsymbol{A}}_{i - 1}},{\mathit{\boldsymbol{A}}_i}} \end{array}} \right] \otimes }\\ {\left[ \begin{array}{l} {\mathit{\boldsymbol{x}}_{i - 1}}\left( {k - 1} \right)\\ {\mathit{\boldsymbol{x}}_i}\left( {k - 1} \right) \end{array} \right] \oplus \left[ \begin{array}{l} {\mathit{\boldsymbol{B}}_{i - 1}}\\ {\mathit{\boldsymbol{B}}_i} \otimes {\mathit{\boldsymbol{C}}_{i - 1}} \otimes {\mathit{\boldsymbol{B}}_{i - 1}} \end{array} \right] \otimes {\mathit{\boldsymbol{u}}_{i - 1}}\left( k \right)} \end{array} $ | (6) |
| $ \begin{array}{l} {\mathit{\boldsymbol{y}}_i}\left( k \right) = \left[ {{\mathit{\boldsymbol{C}}_i} \otimes {\mathit{\boldsymbol{B}}_i} \otimes {\mathit{\boldsymbol{C}}_{i - 1}} \otimes {\mathit{\boldsymbol{A}}_{i - 1}},{\mathit{\boldsymbol{C}}_i} \otimes {\mathit{\boldsymbol{A}}_i}} \right] \otimes \\ \left[ \begin{array}{l} {\mathit{\boldsymbol{x}}_{i - 1}}\left( k \right)\\ {\mathit{\boldsymbol{x}}_i}\left( k \right) \end{array} \right] \oplus \left( {{\mathit{\boldsymbol{C}}_i} \otimes {\mathit{\boldsymbol{B}}_i} \otimes {\mathit{\boldsymbol{C}}_{i - 1}} \otimes {\mathit{\boldsymbol{B}}_{i - 1}}{\mathit{\boldsymbol{u}}_{i - 1}}\left( k \right)} \right) \end{array} $ | (7) |
同理,当存在多个系统模型串联时,同样可以得到合成后的系统状态方程和输出方程。
4 多航空器轨迹优化模型设定存在冲突情形的航空器计划离场时刻不改变,那么它们必然在起飞后后续的多个子航段内进行速度调整。为降低各类人员的工作负荷,在实际系统运行中常将航空器的空中调配转化为地面等待。因此,指挥部门更倾向于调整航空器起飞时刻。此外,为了增强空域航空器流运行的有序性以及提高调配效率,空管部门在特定位置点 (如某一航段的终止点或某一扇区/区域的出口等) 通常依据事先设定的固定时间间隔来移交航空器。从以上调整方案出发,基于所构建的系统状态演化模型,在当前时刻k,依据鲁棒控制原理,从输出变量和控制变量的动态特性出发,可构建优化指标函数如下
| $ \begin{array}{*{20}{c}} {J\left( k \right) = {J_{{\rm{out}}}}\left( k \right) + {J_{{\rm{in}}}}\left( k \right) = }\\ {\sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\sum\limits_{i = 1}^{{n_y}} {{\kappa _i}\left( {k + j} \right)} } + \lambda \sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\sum\limits_{l = 1}^{{n_u}} {{u_l}\left( {k + j} \right)} } } \end{array} $ | (8) |
式中:Np表示预测时域;ny和nu分别表示输出变量和控制变量的数目;κi(k+j) 表示和输出变量相关的指标函数集;λ表示控制变量的权重。根据不同的调控目标,可将该“输出指标函数集”的取值分别设定为
| $ {J_{{\rm{out,1}}}} = \sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\sum\limits_{i = 1}^{{n_y}} {{{\hat y}_i}\left( {k + j\left| k \right.} \right)} } $ | (9) |
| $ {J_{{\rm{out,2}}}} = \sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\sum\limits_{i = 1}^{{n_y}} {\max \left( {{{\hat y}_i}\left( {k + j\left| k \right.} \right) - {r_i}\left( {k + j} \right),0} \right)} } $ | (10) |
| $ {J_{{\rm{out,3}}}} = \sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\sum\limits_{i = 1}^{{n_y}} {\left| {{{\hat y}_i}\left( {k + j\left| k \right.} \right) - {r_i}\left( {k + j} \right)} \right|} } $ | (11) |
式中:ŷi(k+j|k) 表示从当前时刻k开始j个时段后输出变量的预测值,它可由前文所述的系统状态变量和输出变量的迭代过程得到;ri(k+j)表示从当前时刻k开始j个时段后输出变量的期望值。设定指标函数Jout, 1的目的是使航空器尽可能早地到达指定位置点,设定指标函数Jout, 2的目的是使航空器尽可能早地按照预先设定的时刻到达指定位置点且尽可能减小航空器的输出延误,设定指标函数Jout, 3的目的是使航空器尽可能按照预先设定的时刻到达指定位置点,尽可能不延误到达也不提前到达。进一步,为了平衡航路出口处航空器的移交间隔时间,还可以设定如下“输入指标函数”,即
| $ {J_{{\rm{out,4}}}} = \sum\limits_{j = 1}^{{N_p} - 1} {\sum\limits_{i = 1}^{{n_y}} {\left| {{\Delta ^2}{{\hat y}_i}\left( {k + j\left| k \right.} \right)} \right|} } $ | (12) |
式中:
进一步,从“控制变量”层面构建“输入指标函数集”为[17]
| $ {J_{{\rm{in}},1}} = \sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\sum\limits_{l = 1}^{{n_u}} {{u_l}\left( {k + j} \right)} } $ | (13) |
| $ {J_{{\rm{in}},2}} = \sum\limits_{j = 1}^{{N_{\rm{p}}} - 1} {\sum\limits_{l = 1}^{{n_u}} {\left| {{\Delta ^2}{u_l}\left( {k + j} \right)} \right|} } $ | (14) |
设定指标函数Jin, 1的目的是尽可能早地放行航空器进入参考区域以提高空域交通流量,设定Jin, 2指标函数的目的是平衡航路同一入口点处航空器的移交间隔时间,其中Δu(k+j)=u(k+j)-u(k+j-1),其他参数含义同上。此外,为了减少优化控制模型中决策变量的数目以提高求解效率,针对该变量的取值,设定
| $ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{u}}\left( {k + j} \right) = \Delta \mathit{\boldsymbol{u}}\left( {k + {N_c} - 1} \right)}\\ {j = {N_c},{N_c} - 1, \cdots ,{N_p} - 1} \end{array} $ | (15) |
也即Δ2u(k+j)=0,其中Nc表示控制时域且Nc≤Np。综上,从“输入指标”和“输出指标”两类优化指标出发,可以构建如下形式的多航空器无冲突轨迹优化指标函数
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\bar u\left( k \right)} \left\{ {\alpha {J_{{\rm{in}},i}}\left( k \right) + \beta {J_{{\rm{out}},j}}\left( k \right)} \right\}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + j} \right) = \mathit{\boldsymbol{A}} \otimes \mathit{\boldsymbol{x}}\left( {k + j - 1} \right) \oplus \mathit{\boldsymbol{B}} \otimes \mathit{\boldsymbol{u}}\left( {k + j} \right)\\ \mathit{\boldsymbol{y}}\left( {k + j} \right) = \mathit{\boldsymbol{C}} \otimes \mathit{\boldsymbol{x}}\left( {k + j} \right)\\ \Delta \mathit{\boldsymbol{u}}\left( {k + j} \right) \ge 0\;\;\;\;\;j = 0,1, \cdots ,{N_{\rm{p}}} - 1\\ {\Delta ^2}\mathit{\boldsymbol{u}}\left( {k + j} \right) = 0\;\;\;\;j = {N_c},{N_c} + 1, \cdots ,{N_{\rm{p}}} - 1\\ {\mathit{\boldsymbol{A}}_c}\left( k \right)\mathit{\boldsymbol{\tilde u}}\left( k \right) + {\mathit{\boldsymbol{B}}_c}\left( k \right)\mathit{\boldsymbol{\tilde y}}\left( k \right) \le {\mathit{\boldsymbol{C}}_c}\left( k \right) \end{array} \right.} \end{array} $ | (16) |
式中:α和β分别表示调整航空器输入变量和输出变量两种调配方案的权系数;Ac(k),Bc(k) 和Cc(k) 均表示常约束系数。基于所构建优化控制模型,通过选取合适的权系数,可构造多类优化控制方案。
5 算例分析为验证所构建优化控制模型的有效性,在不调整航空器运行速度的前提下,下文将讨论如何仅仅通过调整航空器到达航段入口时刻这一方案来获取多航空器无冲突轨迹。取前文所述的指标函数Jout, 1,以较极端条件下3架航空器的交叉飞行情形为例进行无冲突航迹规划,3架航空器的初始速度分别为v1=610 km/h,v2=770 km/h和v3=890 km/h,各航空器的调速范围均为600 km/h, 900 km/h。航空器运行的航路结构如图 4所示,在初始飞行计划中,航空器1和航空器2分别从左上方和左下方汇聚到航段AB上,航空器3从正左方汇聚到航段AB上,O1和O2分别表示航空器1和航空器2的运行轨迹线与航段AB的交叉点。
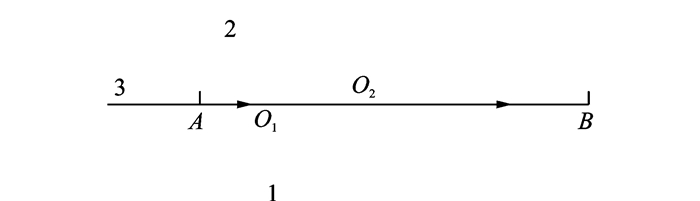
|
图 4 交叉航段结构参数 Figure 4 Parameters of crossover segment |
取dmin=10 km,当航空器1到达位置点O2时,航空器2和航空器3分别到达位置点O1和A,且|AO1|=|O1O2|=20 km,|O2B|=80 km,设定B点为轨迹规划终止点。按照“先到先服务原则”,航段|O2B|对三架航空器的服务顺序分别为航空器1、航空器2和航空器3。在不施加任何调配措施的前提下,基于航空器速度间的差异性,
3架航空器间的运行状况依次呈追赶态势,设定A点为各航空器参考位置原点且航空器1到达位置点O2时的时刻为参考时间原点,在未来某些时刻 (如:第4 00 s) 航空器1和航空器2以及航空器2和航空器3间均不满足最小安全间隔距离。因此,需要依据相关管制规则对各航空器的运行状态进行调整,具体调整方式包括3种情形,即确定性情形、不确定性情形和预测控制情形,各种情形下的仿真基本参数如表 1所示。
| 表 1 多航空器轨迹规划参数 Table 1 Parameters of multi-aircraft trajectory planning |
针对确定性情形,此种调整方式不考虑随机因子的影响,优化模型所涉及到的各类参数均为常量,也即航段对航空器的服务时间以及所设定的缓冲时间均为一个确定性常数。对于前后两架航空器来讲,按照“先到先服务原则”,基于是否融入后一航空器的实际运行速度相关约束条件,可以得到“原始条件”和“放松条件”下各情形航空器的时刻规划结果。针对不确定性情形和预测控制情形,两种调整方式均考虑随机因子的影响,优化模型所涉及到的各类参数均为随机变量,亦即航段对航空器的服务时间以及所设定的缓冲时间均为一个符合特定概率分布的随机变量。本文设定长度为dmin的单位航段对航空器的服务时间t符合以下正态分布,即t~N(μ, σ)。同理,基于是否融入后一航空器的实际运行速度相关约束条件,可以得到“原始条件”和“放松条件”下各情形航空器的时刻规划结果,以上3种情形的轨迹规划结果如表 2所示,其中“AC2”和“AC3”分别代表“航空器2”和“航空器3”。
| 表 2 多航空器轨迹规划结果 Table 2 Results of multi-aircraft trajectory planning |
值得注意的是,本例仅讨论了如何应用直接调整航空器到达航段入口时刻的方案来获取航空器无冲突轨迹,此外,还可以将调整航空器到达航段入口时刻的方案和调整航空器在航段上的运行速度的方案两者结合起来进行使用。
6 结束语依据空域内交通流的运行特征,通过将航路分段并在考虑航路空间结构分布的前提下,在极大代数框架下建立了基于冲突点保护区竞争机制的交通流代数模型。依据空中交通管制规则确定了模型输入变量、状态变量和输出变量之间的关系,基于所设定的多类优化指标函数,采用调整航空器过冲突点时刻和初始放行时刻两种策略,建立了多航空器无冲突鲁棒轨迹规划模型。未来的研究将侧重于分析输入扰动对输出之间的关系,进而分析输出受输入影响的敏感性。
| [1] |
吕小平.
中国民航新一代空中交通管理系统发展总体框架[J]. 中国民用航空, 2007, 80(8): 24–26.
LÜ Xiaoping. The development framework of next generation civil aviation air traffic management system[J]. China Civil Aviation, 2007, 80(8): 24–26. |
| [2] | LYMPEROPOULOS I, LYGEROS J, LECCHINI A.Model based aircraft trajectory prediction during takeoff[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Keystone, Colorado, USA:AIAA, 2006:1-12. |
| [3] |
马博敏, 杨红雨, 余静.
一种基于实时航迹的流量预测修正算法[J]. 微计算机信息, 2010, 26(2): 186–187.
MA Bomin, YANG Hongyu, YU Jing. A flow forcast amending algorithm based on real-time track[J]. Micro Computer Information, 2010, 26(2): 186–187. |
| [4] |
刘恒泽, 杨刚, 张长革, 等.
相互作用多模型跟踪过程中的航迹外推算法[J]. 现代电子技术, 2010(15): 5–7.
LIU Hengze, YANG Gang, ZHANG Changge, et al. Flight path extrapolation algorithm in target tracking by IMM[J]. Modern Electronics Technique, 2010(15): 5–7. |
| [5] |
韩云祥, 汤新民, 韩松臣, 等.
基于微分Petri网的民机航迹演化通用模型构建[J]. 南京航空航天大学学报, 2014, 46(2): 322–328.
HAN Yunxiang, TANG Xinmin, HAN Songchen, et al. Construction of civil aircraft trajectory evolution general model based on differential Petri-net[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(2): 322–328. |
| [6] | SAHAWNEH L R, MACKIE J, SPENCER J, et al. Airborne radar-based collision detection and risk estimation for small unmanned aircraft systems[J]. Journal of Aerospace Information Systems, 2015, 12(7): 1–11. |
| [7] | YONG K K, HAN J W, PARK H. Trajectory prediction for using real data and real meteorological data[J]. Lecture Notes in Electrical Engineering, 2015: 89–103. |
| [8] | HONG S, LEE K. Trajectory prediction for vectored area navigation arrivals[J]. Journal of Aerospace Information Systems, 2015, 12(7): 490–502. DOI:10.2514/1.I010245 |
| [9] | BESADA J A, FRONTERA G, CRESPO J B, et al. Automated aircraft trajectory prediction based on formal intent-related language processing[J]. IEEE Transa ctionson Intelligent Transportation Systems, 2013, 14(3): 1067–1082. DOI:10.1109/TITS.2013.2252343 |
| [10] | THIPPHAVONG D P, SCHULTZ C A, LEE A G, et al. Adaptive algorithm to improve trajectory prediction accuracy of climbing aircraft[J]. Journal of Guidance, Control, and Dynamics, 2012, 36(1): 15–24. |
| [11] | Tastambekov K, Puechmorel S, Delahaye D, et al. Aircraft trajectory forecasting using local functional regression in Sobolev space[J]. Trans portation Research Part C:Emerging Technologies, 2014, 39: 1–22. DOI:10.1016/j.trc.2013.11.013 |
| [12] | ALLIGIER R, GIANAZZA D, DURAND N. Learning the aircraft mass and thrust to improve the ground-based trajectory prediction of climbing flights[J]. Transportation Research Part C:Emerging Technologies, 2013, 36(9): 45–60. |
| [13] | MATSUNO Y, TSUCHIYA T, WEI J, et al. Stochastic optimal control for aircraft conflict resolution under wind uncertainty[J]. Aerospace Science and Technology, 2015, 43: 77–88. DOI:10.1016/j.ast.2015.02.018 |
| [14] | OMER J. A space-discretized mixed-integer linear model for air-conflict resolution with speed and heading maneuvers[J]. Computers & Operations Research, 2015, 58: 75–86. |
| [15] | CLEMENTS J C. The optimal control of collision avoidance trajectories in air traffic management[J]. Transportation Research Part B:Methodological, 1999, 33(4): 265–280. DOI:10.1016/S0191-2615(98)00031-9 |
| [16] | GOVERDE R M, BOVY P H, OLSDER G.The max-plus algebra approac h to transportation problems[C]//World Transport Research:Selected Proceeding s of the 8th World Conference on Transport Research.Antwerp, Belgium:Elsevier, 1999:377-390. |
| [17] | DESCHUTTER B, VANDEN T J J. Model predictive control for max-plus-linear discrete event systems[J]. Automatica, 2001, 37: 1049–1056. DOI:10.1016/S0005-1098(01)00054-1 |
| [18] | VANDEN T J J, DESCHUTTER B. Model predictive control for perturbed max-plus-linear systems[J]. Systems & Control Letters, 2002, 45(3): 21–33. |
| [19] | COHEN G, EACUTE S, GAUBERT P, et al. Max-plus algebra and system theory:Where we are and where to go now[J]. Annual Reviews in Control, 1999, 23(1): 207–219. DOI:10.1016/S1367-5788(99)00023-1 |
| [20] |
韩云祥, 汤新民, 张明.
一类无冲突轨迹规划方案[J]. 控制理论与应用, 2015, 32(7): 918–924.
HAN Yunxiang, TANG Xinmin, ZHANG Ming. Conflict-free trajectory planning scheme[J]. Control Theory & Applications, 2015, 32(7): 918–924. |
| [21] |
韩云祥.固定航路飞行条件下航空器航迹规划若干关键技术研究[D].南京:南京航空航天大学, 2014.
HAN Yunxiang.Research on key issues of aircraft trajectory planni ng in fixed route[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2014. |
 2017, Vol. 49
2017, Vol. 49


