齿轮分流传动系统,又称为功率分流传动系统。为进一步提高直升机传动系统的性能,在直升机主减速器传动系统中提出了具有齿轮动力分流的传动构型。与传统的行星齿轮传动构型相比,分流传动构型具有以下优点[1-2]:(1) 分流传动的最后一级减速比可达14∶1,这对降低传动系统的重量极其有利;(2) 减速级数减少,最后一级传动比很大,因此整个传动系统的传动级数会减少;(3) 传动系统可靠性高。行星齿轮传动机构中行星轮较多且支承结构复杂,易出故障。采用分流传动构型时,齿轮和轴承数量减少,且分流构型轮系为定轴轮系传动,技术上比较成熟,因此传动系统的可靠性提高;(4) 噪声低。开展分流传动系统的构型及技术研究,对提高直升机传动系统的功重比、可靠性和降低噪声污染,提升我国直升机传动系统的自主创新发展等具有重要的意义,能带来巨大的经济效益和社会效益。
鉴于齿轮分流传动系统的诸多优点及其在特殊传动系统中的独特作用,国内外学者[3-11]已经对齿轮分流传动系统的动力学特性,包括系统的固有频率和动载系数等开展了广泛的研究。文献资料表明,在上述的相关研究中,通常将支承刚度这一参数按照常数进行处理,忽略了滚动轴承自身结构的复杂性所导致的支承刚度的波动[12]。本文以圆柱齿轮分流传动系统为研究对象,考虑时变啮合刚度、综合传递误差、齿侧间隙等因素,建立了含时变支承刚度的弯扭耦合动力学模型,并重点分析了时变支承刚度对系统振动特性的影响,这为齿轮分流传动系统的设计与研究提供了一定的理论支撑。
1 齿轮分流传动系统的动力学模型图 1为圆柱齿轮分流传动系统示意图,其工作原理为:功率经输入齿轮Zp传递给分流级大齿轮ZLs和ZRs,再由双联轴经并车级小齿轮ZLh和ZRh汇流至输出齿轮ZB,从而实现功率的分流与并车。

|
图 1 圆柱齿轮分流传动系统示意图 Figure 1 Sketch of split torque transmission system |
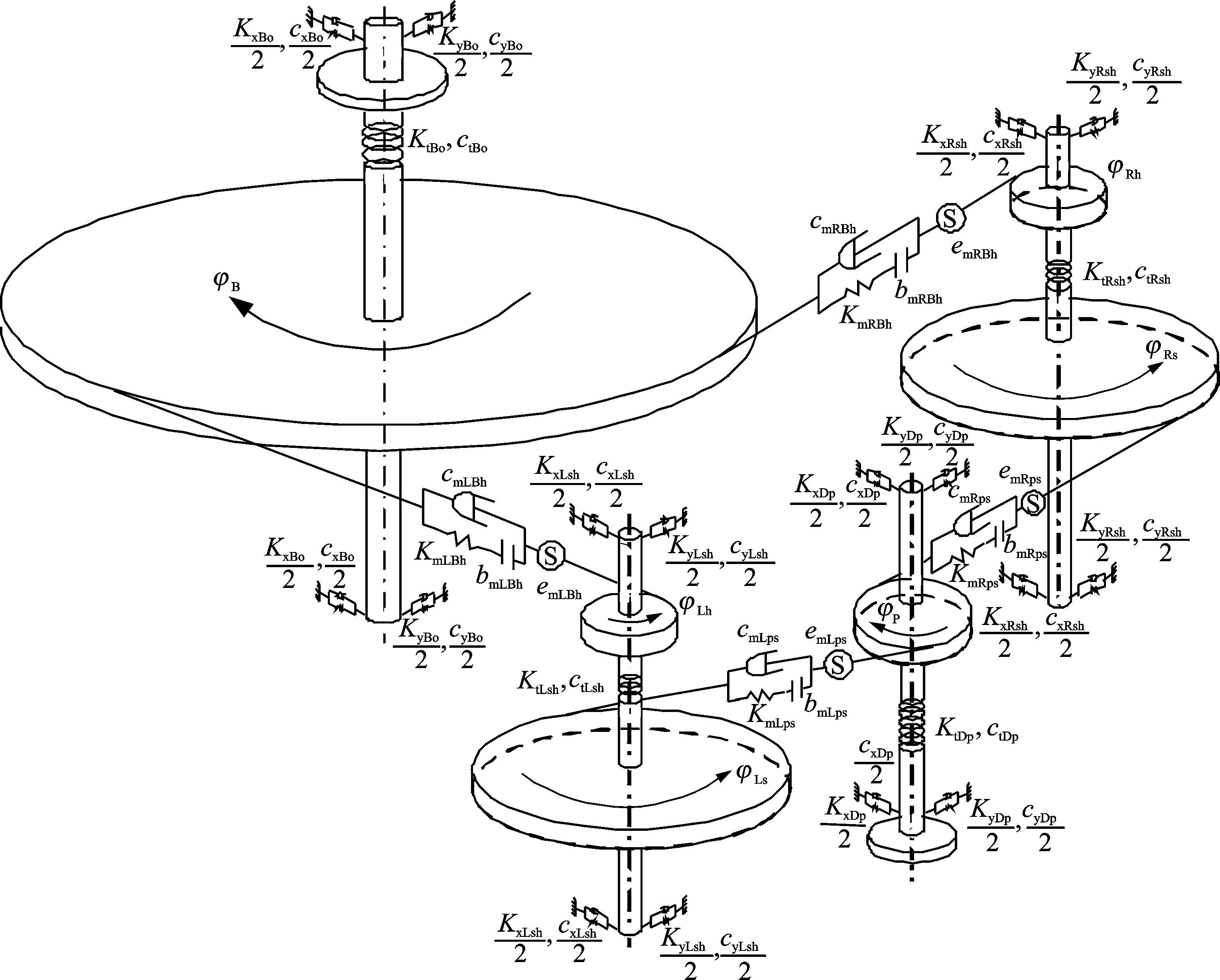
为便于建立动力学方程,将齿轮副之间啮合变形、轴的扭转变形和支承变形等效为弹簧连接,应用集中质量法建立如图 2所示的弯扭耦合动力学模型。图中:KmLps和KmLBh、KmRps和KmRBh分别表示左、右分支的分扭级和并车级齿轮副间的时变啮合刚度;c、e和b分别表示啮合阻尼、啮合误差和齿侧间隙,下标与时变啮合刚度相同;Ktn和ctn(n=Dp、Rsh、Lsh、Bo)分别表示输入轴、右分支双联轴、左分支双联轴、输出轴的扭转刚度和扭转阻尼;Kxn、Kyn和cxn、cyn分别表示相应轴的x、y方向的支承刚度和支承阻尼。
|
图 2 圆柱齿轮分流传动系统的弯扭耦合动力学模型 Figure 2 Bending-torsional coupled dynamic model of split torque transmission system |
则该系统共有16个自由度,可用向量Y表示为
| $\begin{align} & Y=({{\varphi }_{D}},{{\varphi }_{p}},{{\varphi }_{Rs}},{{\varphi }_{Rh}},{{\varphi }_{Ls}},{{\varphi }_{Lh}},{{\varphi }_{B}},{{\varphi }_{o}}, \\ & {{X}_{p}},{{Y}_{p}},{{X}_{R}},{{Y}_{R}},{{X}_{L}},{{Y}_{L}},{{X}_{B}},{{Y}_{B}}) \\ \end{align}$ | (1) |
式中:φD、φo分别表示输入端、输出端的扭转微位移;φp、φRs、φRh、φLs、φLh、φB则分别表示相应齿轮的扭转微位移;Xp和Yp、XR和YR、XL和YL、XB和YB分别表示输入轴、右双联轴、左双联轴、输出轴沿广义坐标系x和y方向的振动微位移。
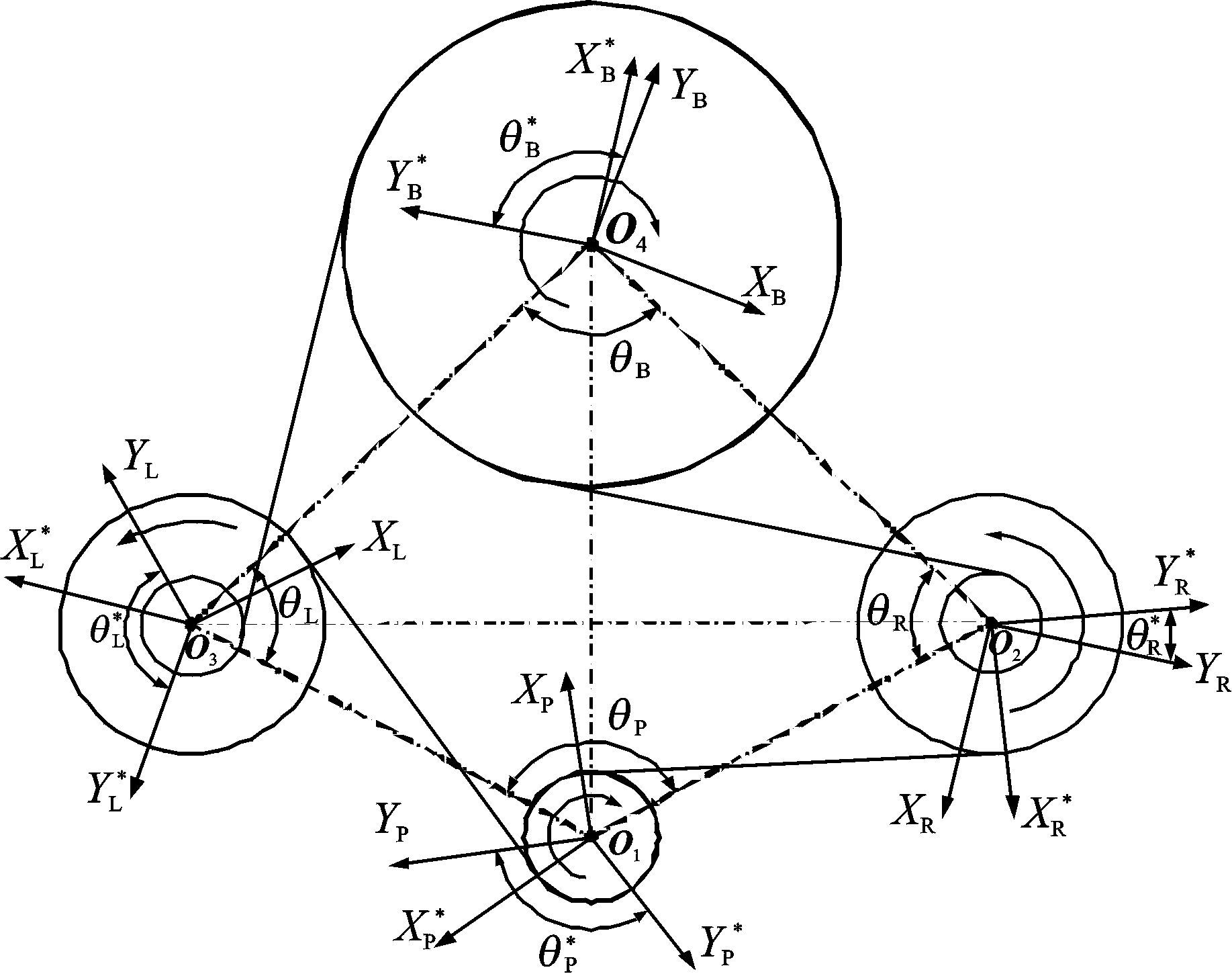
2 齿轮分流传动系统振动微分方程为便于动力学方程的分析,引入广义坐标和局部坐标来描述齿轮副之间的啮合关系,如图 3所示。图中:带有“*”的为局部坐标系,Y和Y*的方向与齿轮啮合线方向相同;θp、θR、θL、θB分别表示各齿轮中心连线的夹角;θp*、θR*、θL*、θB*则分别表示Yp和Yp*、YR和YR*、YL和YL*、YB和YB*之间的夹角。根据图 3中的几何关系,广义坐标和局部坐标之间的转换关系为
| $\left\{ \begin{align} & {{X}_{k}}^{*}~=\text{ }{{X}_{k~}}cos{{\theta }_{k~}}^{*}~+\text{ }{{Y}_{k~}}sin{{\theta }_{k~}}^{*} \\ & {{Y}_{k}}^{*}~=-{{X}_{k~}}sin{{\theta }_{k~}}^{*}~+\text{ }{{Y}_{k~}}cos{{\theta }_{k~}}^{*} \\ \end{align} \right.$ | (2) |
式中:k=P、R、L、B,其中,θp*=θp,θB*=θB,θR*和θL*分别为(θR+α1+α2-π)和(θL-α1-α2+π);α1、α2为分流级和并车级齿轮的压力角。
|
图 3 局部坐标与广义坐标关系图 Figure 3 Relationship of partial and generalized coordinates of system |
齿轮副间的等效啮合位移可表示为
| $\left\{ \begin{align} & {{Y}_{mRps}}=(-{{Y}_{p}}+{{\varphi }_{p}}{{r}_{bp}})-({{Y}_{R}}^{*}+{{\varphi }_{Rs}}{{r}_{bRs}})-{{e}_{mRps}} \\ & {{Y}_{mLps}}=(-{{Y}_{p}}^{*}+{{\varphi }_{p}}{{r}_{bp}})-({{Y}_{L}}+{{\varphi }_{Ls}}{{r}_{bLs}})-{{e}_{mLps}} \\ & {{Y}_{mRBh}}=(-{{Y}_{R}}+{{\varphi }_{Rh}}{{r}_{bRh}})-({{Y}_{B}}^{*}+{{\varphi }_{B}}{{r}_{bB}})-{{e}_{mRBh}} \\ & {{Y}_{mLBh}}=(-{{Y}_{L}}^{*}+{{\varphi }_{Lh}}{{r}_{bLh}})-({{Y}_{B}}+{{\varphi }_{B}}{{r}_{bB}})-{{e}_{mLBh}} \\ \end{align} \right.$ | (3) |
为消除刚体位移,统一结构单位,将式(1) 中的角位移转换为线位移,则有
| $\left\{ \begin{align} & {{Y}_{Dp}}={{r}_{Dp}}({{\varphi }_{D}}-{{\varphi }_{p}}) \\ & {{Y}_{Rsh}}={{r}_{Rsh}}({{\varphi }_{Rs}}-{{\varphi }_{Rh}}) \\ & {{Y}_{Lsh}}={{r}_{Lsh}}({{\varphi }_{Ls}}-{{\varphi }_{Lh}}) \\ & {{Y}_{Bo}}={{r}_{Bo}}({{\varphi }_{B}}-{{\varphi }_{o}}) \\ \end{align} \right.$ | (4) |
式中:rDp、rRsh、rLsh和rBo分别表示输入轴、右分支双联轴、左分支双联轴和输出轴的半径。结合式(2~4) ,可消除一个刚体位移,则YmLBh可由其他线位移表示为
| $\begin{align} & {{Y}_{mLBh}}={{Y}_{mRBh}}-\left( Y{{_{L}^{*}}^{}}+{{Y}_{B}} \right)+\left( {{e}_{mRBh}}-{{e}_{mLBh}} \right)+ \\ & {{\left( {{Y}_{R}}+Y_{B}^{*} \right)}^{}}-\frac{{{r}_{bLh}}}{{{r}_{Lsh}}}{{Y}_{Lsh}}+\frac{{{r}_{bRh}}}{{{r}_{Rsh}}}{{Y}_{Rsh}}+ \\ & \frac{{{r}_{bRh}}}{{{r}_{bRs}}}({{Y}_{mRps}}+{{Y}_{p}}+Y{{_{R}^{*}}^{}}+{{e}_{mRps}})- \\ & \frac{{{r}_{bLh}}}{{{r}_{bLs}}}\left( {{Y}_{mLps}}+Y{{_{p}^{*}}^{}}+{{Y}_{L}}+{{e}_{mLps}} \right) \\ \end{align}$ | (5) |
根据齿轮分流传动系统的动力学模型,则该传动系统的动力学方程为
| $\left\{ \begin{align} & {{I}_{D}}{{{\ddot{\varphi }}}_{D}}+{{K}_{tDp}}({{\varphi }_{D}}-{{\varphi }_{p}})+{{c}_{tDp}}({{{\dot{\varphi }}}_{D}}-{{{\dot{\varphi }}}_{p}})={{T}_{D}} \\ & {{I}_{p}}{{{\ddot{\varphi }}}_{p}}+{{K}_{tDp}}({{\varphi }_{p}}-{{\varphi }_{D}})+{{c}_{tDp}}({{{\dot{\varphi }}}_{p}}-{{{\dot{\varphi }}}_{D}})= \\ & (-{{F}_{mRps}}-{{F}_{mLps}}){{r}_{bp}} \\ & ({{m}_{D}}+{{m}_{p}}){{{\ddot{X}}}_{p}}+{{K}_{xDp}}{{X}_{p}}+{{c}_{xDp}}{{{\dot{X}}}_{p}}={{F}_{xp}} \\ & ({{m}_{D}}+{{m}_{p}}){{{\ddot{Y}}}_{p}}+{{K}_{yDp}}{{Y}_{p}}+{{c}_{yDp}}{{{\dot{Y}}}_{p}}={{F}_{yp}} \\ & {{I}_{Rs}}{{{\ddot{\varphi }}}_{Rs}}+{{K}_{tRsh}}({{\varphi }_{Rs}}-{{\varphi }_{Rh}})+{{c}_{tRsh}}({{{\dot{\varphi }}}_{Rs}}-{{{\dot{\varphi }}}_{Rh}})={{F}_{mRps}}{{r}_{bRs}} \\ & {{I}_{Rh}}{{{\ddot{\varphi }}}_{Rh}}+{{K}_{tRsh}}({{\varphi }_{Rh}}-{{\varphi }_{Rs}})+{{c}_{tRsh}}({{{\dot{\varphi }}}_{Rh}}-{{{\dot{\varphi }}}_{Rs}})= \\ & -{{F}_{mRBh}}{{r}_{bRh}} \\ & ({{m}_{Rs}}+{{m}_{Rh}}){{{\ddot{X}}}_{R}}+{{K}_{xRsh}}{{X}_{R}}+{{c}_{xRsh}}{{{\dot{X}}}_{R}}={{F}_{xR}} \\ & ({{m}_{Rs}}+{{m}_{Rh}}){{{\ddot{Y}}}_{R}}+{{K}_{yRsh}}{{Y}_{R}}+{{c}_{yRsh}}{{{\dot{Y}}}_{R}}={{F}_{yR}} \\ & {{I}_{Ls}}{{{\ddot{\varphi }}}_{Ls}}+{{K}_{tLsh}}({{\varphi }_{Ls}}-{{\varphi }_{Lh}})+{{c}_{tLsh}}({{{\dot{\varphi }}}_{Ls}}-{{{\dot{\varphi }}}_{Lh}})={{F}_{mLps}}{{r}_{bLs}} \\ & {{I}_{Lh}}{{{\ddot{\varphi }}}_{Lh}}+{{K}_{tLsh}}({{\varphi }_{Lh}}-{{\varphi }_{Ls}})+{{c}_{tLsh}}({{{\dot{\varphi }}}_{Lh}}-{{{\dot{\varphi }}}_{Ls}})= \\ & -{{F}_{mLBh}}{{r}_{bLh}} \\ & ({{m}_{Ls}}+{{m}_{Lh}}){{{\ddot{X}}}_{L}}+{{K}_{xLsh}}{{X}_{L}}+{{c}_{xLsh}}{{{\dot{X}}}_{L}}={{F}_{xL}} \\ & ({{m}_{Ls}}+{{m}_{Lh}}){{{\ddot{Y}}}_{L}}+{{K}_{yLsh}}{{Y}_{L}}+{{c}_{yLsh}}{{{\dot{Y}}}_{L}}={{F}_{yL}} \\ & {{I}_{B}}{{{\ddot{\varphi }}}_{B}}+{{K}_{tBo}}({{\varphi }_{B}}-{{\varphi }_{o}})+{{c}_{tBo}}({{{\dot{\varphi }}}_{B}}-{{{\dot{\varphi }}}_{o}})= \\ & ({{F}_{mRBh}}+{{F}_{mLBh}}){{r}_{bB}} \\ & {{I}_{o}}{{{\ddot{\varphi }}}_{o}}+{{K}_{tBo}}({{\varphi }_{o}}-{{\varphi }_{B}})+{{c}_{tBo}}({{{\dot{\varphi }}}_{o}}-{{{\dot{\varphi }}}_{B}})=-{{T}_{o}} \\ & ({{m}_{B}}+{{m}_{o}}){{{\ddot{X}}}_{B}}+{{K}_{xBo}}{{X}_{B}}+{{c}_{xBo}}{{{\dot{X}}}_{B}}={{F}_{xB}} \\ & ({{m}_{B}}+{{m}_{o}}){{{\ddot{Y}}}_{B}}+{{K}_{yBo}}{{Y}_{B}}+{{c}_{yBo}}{{{\dot{Y}}}_{B}}={{F}_{yB}} \\ \end{align} \right.$ | (6) |
式中:mD和mo分别为输入端和输出端的质量;mp、mRs、mRh、mLs、mLh和mB则分别表示输入齿轮Zp、右分支分扭级大齿轮ZRs、右分支并车级小齿轮ZRh、左分支分扭级大齿轮ZLs、左分支并车级小齿轮ZLh和输出齿轮ZB的质量;rbp、rbRs、rbRh、rbLs、rbLh、和rbB分别表示相应齿轮的基圆半径;FmLps和FmLBh 、FmRps和FmRBh分别为左、右分支分扭级和并车级齿副间啮合力;Fxp和Fyp、FxL和FyL、FxR和FyR、FxB和FyB分别为齿副间啮合力沿传动轴的广义坐标x和y方向分解后的合力。各轴x、y方向的合力和齿轮副间啮合力分别如式(7,8) 所示。
| $\left\{ \begin{align} & {{F}_{xp}}=-sin({{\theta }_{p}}){{F}_{mLps}},{{F}_{yp}}=cos({{\theta }_{p}}){{F}_{mLps}}+{{F}_{mRps}} \\ & {{F}_{xR}}=-sin({{\theta }_{R}}){{F}_{mRps}},{{F}_{yR}}=cos({{\theta }_{R}}){{F}_{mRps}}+{{F}_{mRBh}} \\ & {{F}_{xL}}=-sin({{\theta }_{L}}){{F}_{mLBh}},{{F}_{yL}}=cos({{\theta }_{L}}){{F}_{mLBh}}+{{F}_{mLps}} \\ & {{F}_{xB}}=-sin({{\theta }_{B}}){{F}_{mRBh}},{{F}_{yB}}=cos({{\theta }_{B}}){{F}_{mRBh}}+{{F}_{mLBh}} \\ \end{align} \right.$ | (7) |
| ${{F}_{m~}}_{i~}=\text{ }{{K}_{mi~}}{{f}_{mi~}}({{Y}_{mi~}})\text{ }+\text{ }{{c}_{mi~}}{{{\dot{Y}}}_{mi~}}$ | (8) |
式中:Kmi、fmi和cmi分别表示齿轮啮合刚度均值、齿侧间隙函数和啮合阻尼,下标i分别表示Rps、RBh、Lps和LBh。齿侧间隙函数fmi(Ymi)可表示为
| ${{f}_{m~}}_{i~}({{Y}_{mi~}})\text{ }=\left\{ \begin{matrix} {{Y}_{mi~}}-{{b}_{mi}} & {{Y}_{mi}}>\text{ }{{b}_{mi}} \\ 0 & -{{b}_{mi~}}<{{Y}_{mi~}}<\text{ }{{b}_{mi}} \\ {{Y}_{mi~}}+\text{ }{{b}_{mi~}} & {{Y}_{mi~}}<\text{ }-{{b}_{mi}} \\ \end{matrix} \right.$ | (9) |
联立式(2~9) ,可获得消除刚体位移后的动力学方程。为提高计算精度,还需要对微分方程进行量纲化处理。本文采用4~5阶变步长Runge-Kutta法对系统的非线性振动微分方程进行求解,从而获得系统的位移响应。
3 支承刚度与动载系数 3.1 轴承非时变支承刚度在滚动轴承内外圈的承载方向上,将产生单位相对位移时的载荷大小定义为轴承的等效支承刚度K[13],即
| $K=\frac{dF}{d\delta }$ | (10) |
式中:F为滚动轴承承受的载荷;δ为轴承承载方向上内外圈之间的相对变形量。为简化计算,通常在静力学条件下进行处理。因此,F为齿轮副间平均啮合力作用下轴承承受的载荷;δ为该静载荷下的轴承径向变形量。
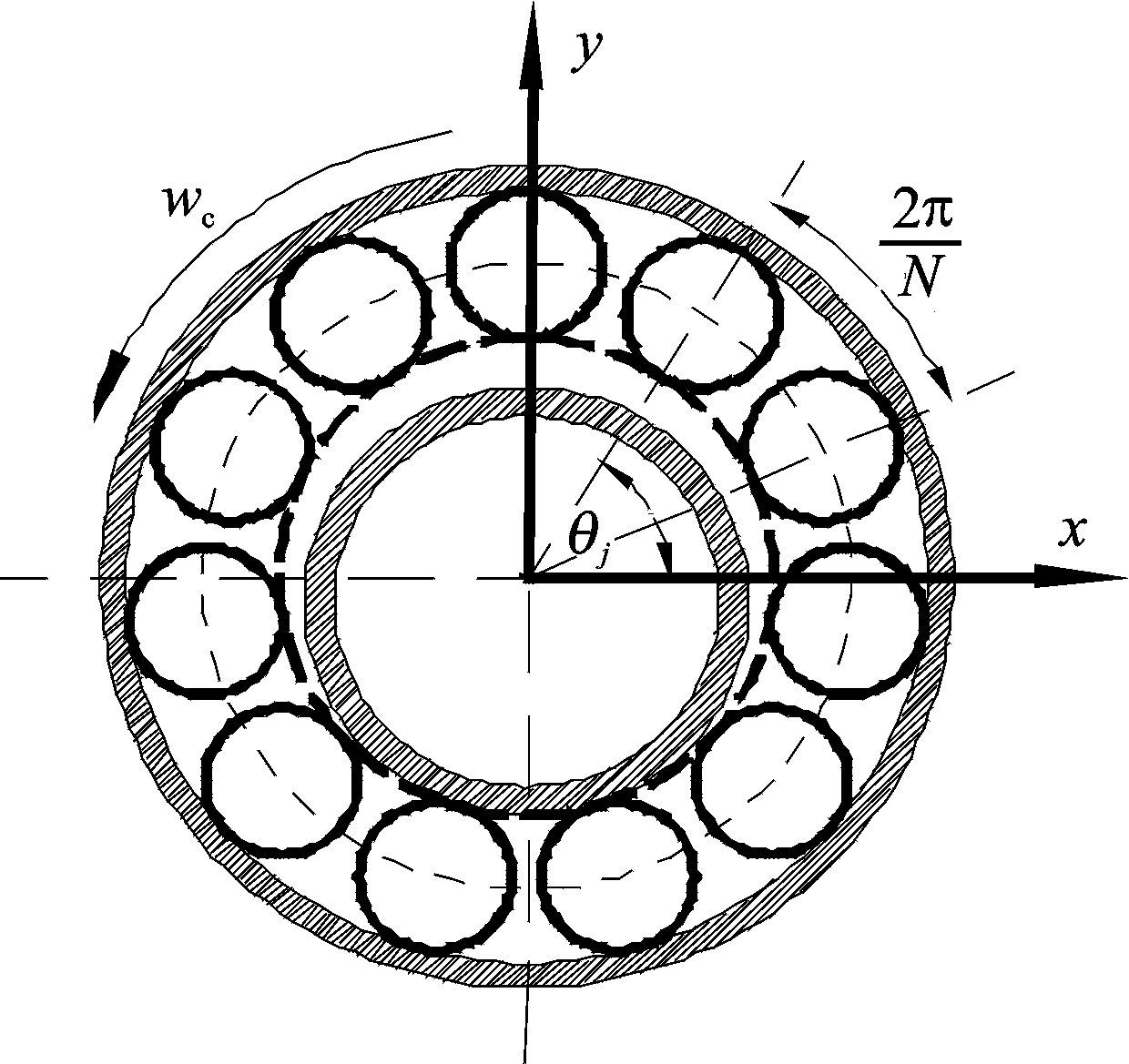
3.2 轴承时变支承刚度轴承结构非常复杂,即使滚动体在几何上处于理想状态,滚动轴承本身也会因为滚动体在保持架中位置的变化产生振动。根据赫兹接触理论,不同滚动体之间载荷的转换以及轴承间隙的存在,会造成滚动轴承刚度的波动,表现出时变性和非线性特征。根据文献[14, 15],忽略滚子本身的质量、惯性,假设滚动体与滚道之间为纯滚动,可将轴承简化为两自由度系统,如图 4所示。图中:θj为第j个滚子在t时刻的位置角;ωc为轴承保持架转速;N为滚子数目。位置角θj在t时刻的表达式为
| ${{\theta }_{j}}={{\psi }_{0}}+{{\omega }_{c}}t+\frac{2\pi }{N}\left( j-1 \right)$ | (11) |
式中ψ0为第j个滚子的初始位置角。
将每个滚子所受的载荷分别投影至x、y方向,根据赫兹接触理论及受力平衡条件可得轴承x、y方向的分力fx和fy为
| $\left\{ \begin{align} & {{f}_{x}}=\sum\limits_{j=1}^{N}{{{Q}_{j}}cos({{\theta }_{j}})} \\ & {{f}_{y}}=\sum\limits_{j=1}^{N}{{{Q}_{j}}sin({{\theta }_{j}})} \\ \end{align} \right.$ | (12) |
式中Qj为第j个滚子与套圈之间的接触载荷。其中,Qj可表示为
| ${{Q}_{j}}={{k}_{c}}\delta {{({{\theta }_{j}})}^{n}}{{\gamma }_{j}}$ | (13) |
| $\delta ({{\theta }_{j}})={{x}_{s}}cos({{\theta }_{j}})+{{y}_{s}}sin({{\theta }_{j}})-e$ | (14) |
式中:kc为接触变形因子,与材料和轴承类型有关;δ(θj)为第j个滚子的总接触变形量,是位置角θj、轴承内圈相对外圈的位移量xs和ys、以及轴承间隙e的函数;γj为接触状态函数,当变形量大于零时取1,变形量小于等于零时取0;n为指数,球轴承时取1.5,滚子轴承时取1.1。
|
图 4 滚动轴承模型示意图 Figure 4 Sketch of models of rolling element bearing |
则轴承的时变刚度可通过如下定义求出[12]
| $\left[ \begin{matrix} {{K}_{x}} \\ {{K}_{y}} \\ \end{matrix} \right]=\frac{df}{d\delta }=\left[ \begin{matrix} \frac{d{{f}_{x}}}{dx} \\ \frac{d{{f}_{y}}}{dy} \\ \end{matrix} \right]$ | (15) |
动载系数是衡量齿轮之间啮合力受振动影响的程度,通常定义齿轮副间的动载系数为
| $G=\frac{kx\left( t \right)+c\dot{x}\left( t \right)}{P}$ | (16) |
式中:k为齿轮副平均啮合刚度;c为啮合阻尼;x(t)和${\dot{x}}$(t)分别表示啮合线上相对位移和相对速度;P为齿轮副间的静载荷。
4 齿轮分流传动系统的动力学特性仿真分析该传动系统的基本参数如下:输入转速为3 000 r/min,输入功率为150 kW,综合传递误差幅值为10 μm,齿侧间隙为100 μm,其余参数如表 1所示。轴承的结构参数如表 2所示。其中,bDp表示输入轴上的轴承;bLsh、bRsh分别表示左右分支双联轴上的轴承;bBo表示输出轴上的轴承。输入轴、双联轴和输出轴的两端分别采用同样型号的轴承,且左右分支双联轴上轴承完全相同。
| 表 1 系统基本参数 Table 1 Essential parameters of system |
| 表 2 轴承的结构参数 Table 2 Structural parameters of bearings |
4.1 滚动轴承支承刚度的时变性
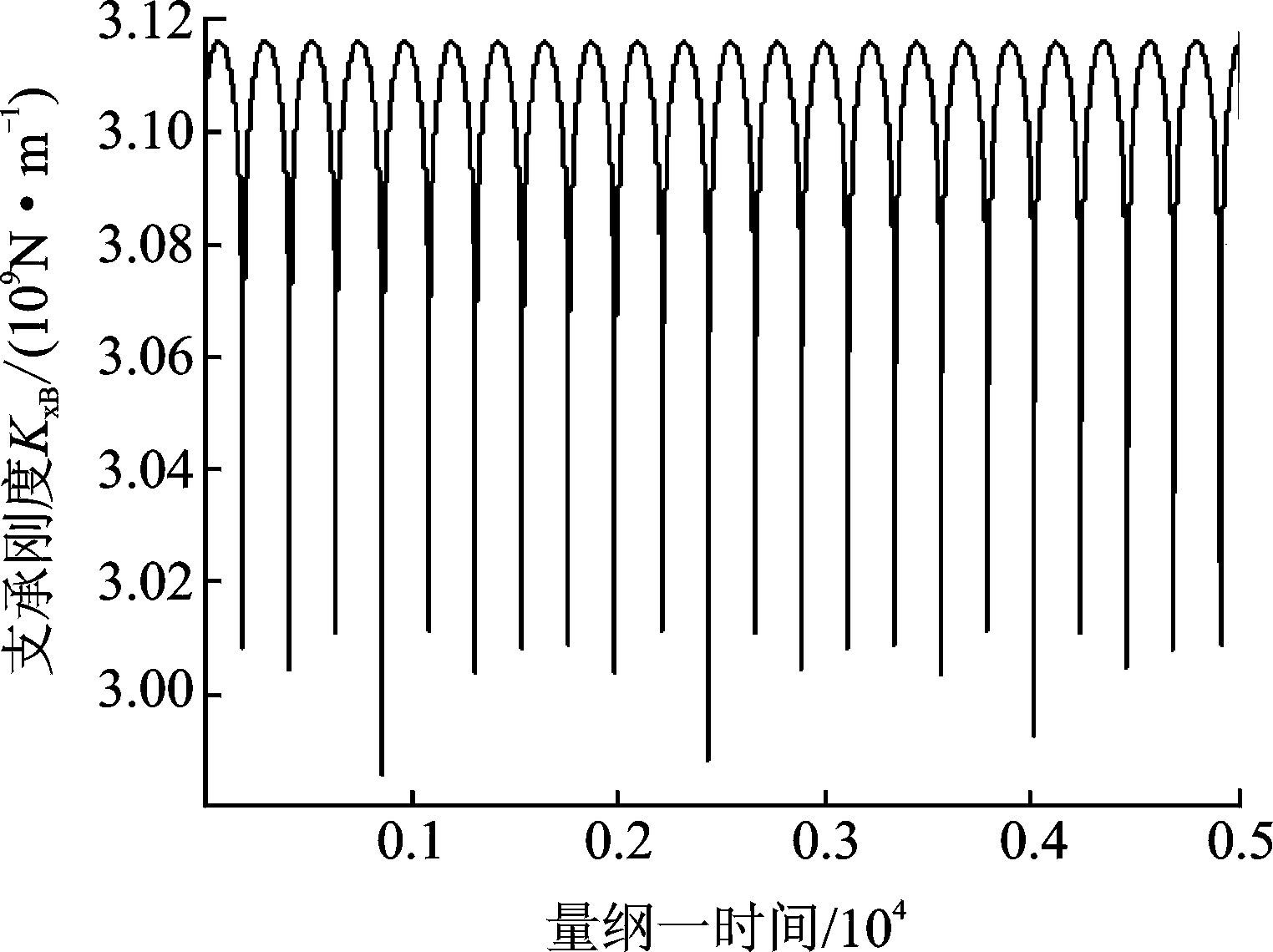
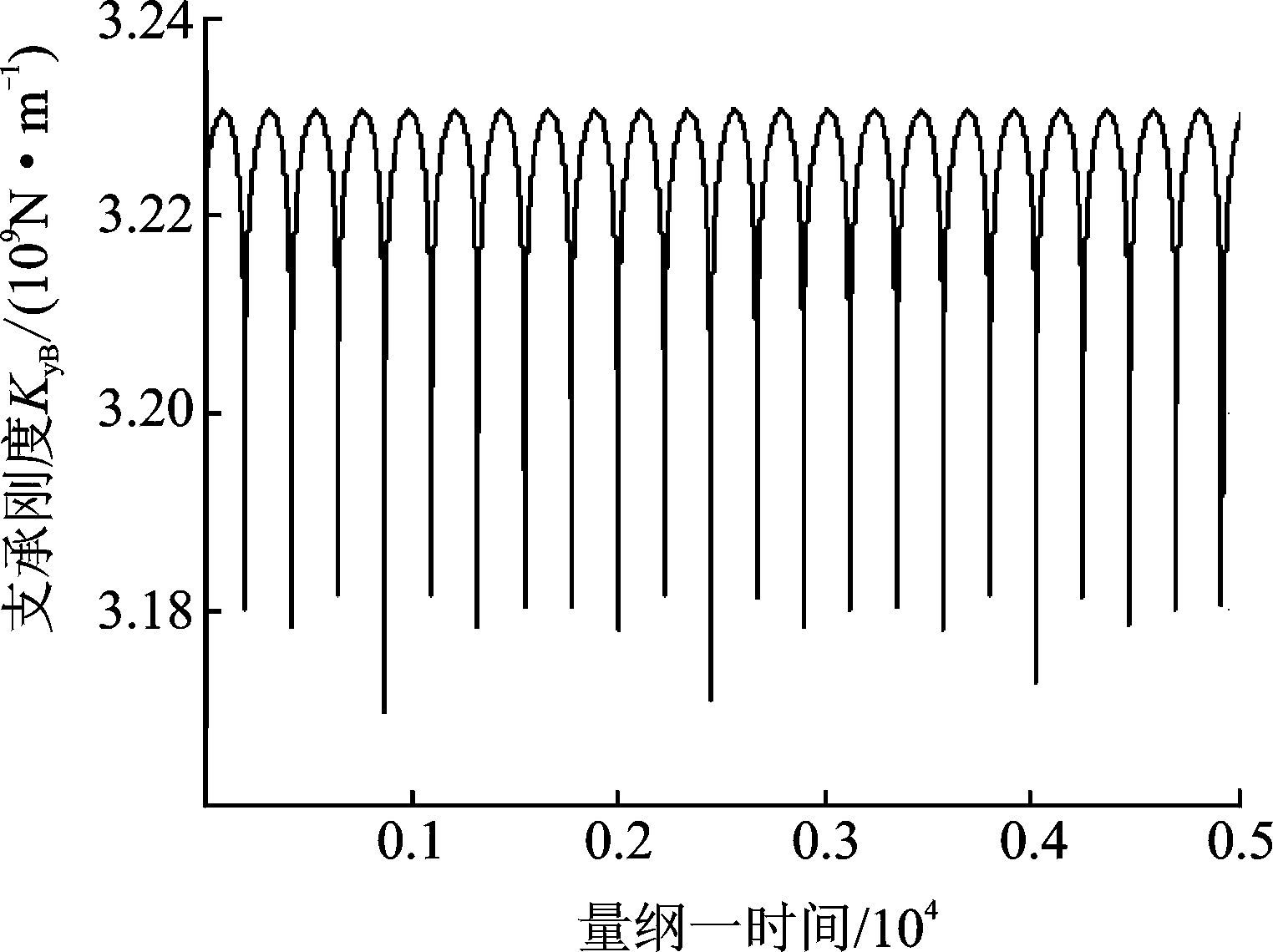
根据上述理论分析,将滚动轴承的支承刚度按照时变模型处理,可获得支承刚度随时间的变化规律。输出轴横向上沿广义坐标x、y方向的时变支承刚度如图 5和图 6所示。由图可知,输出轴的x、y方向的支承刚度在3×109 N/m附近波动,表现出时变性和非线性的特点。
|
图 5 输出轴x方向支承刚度 Figure 5 Supporting stiffness of output shaft in x direction |
|
图 6 输出轴y方向支承刚度 Figure 6 Supporting stiffness of output shaft in y direction |
4.2 时变支承刚度对系统动态响应的影响
为分析支承刚度对传动系统动力学特性的影响,分别将非时变支承刚度、时变支承刚度代入齿轮分流传动系统动力学方程中。研究结果表明,当按照滚动轴承时变模型进行计算时,输出轴上的刚度波动较为明显,因此主要考察输出轴上的横向振动位移XB、YB的响应,结果如图 7~10所示。
|
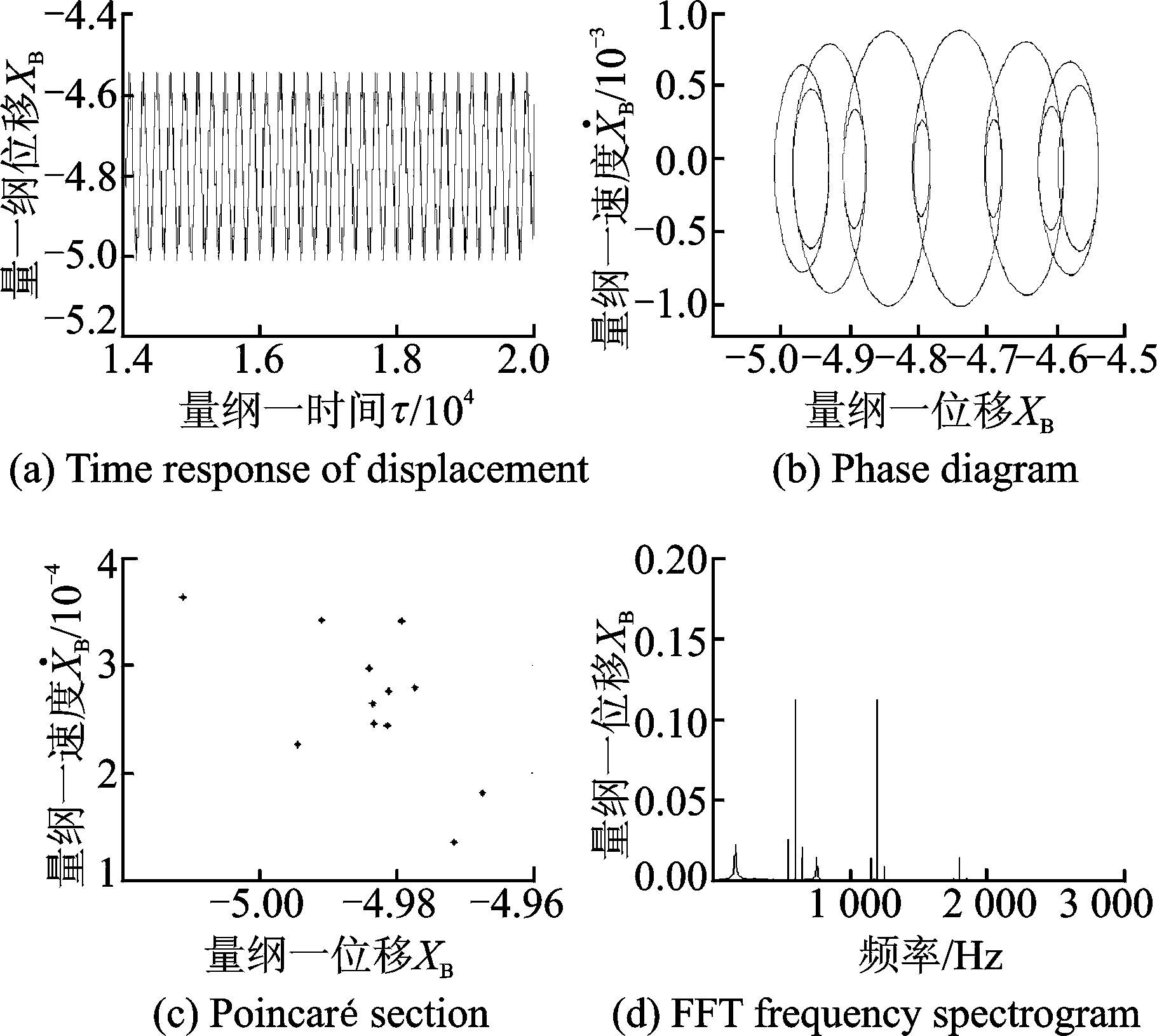
图 7 非时变支承刚度下XB的响应 Figure 7 Dynamic responses of XB under time-invariant supporting stiffness |
|
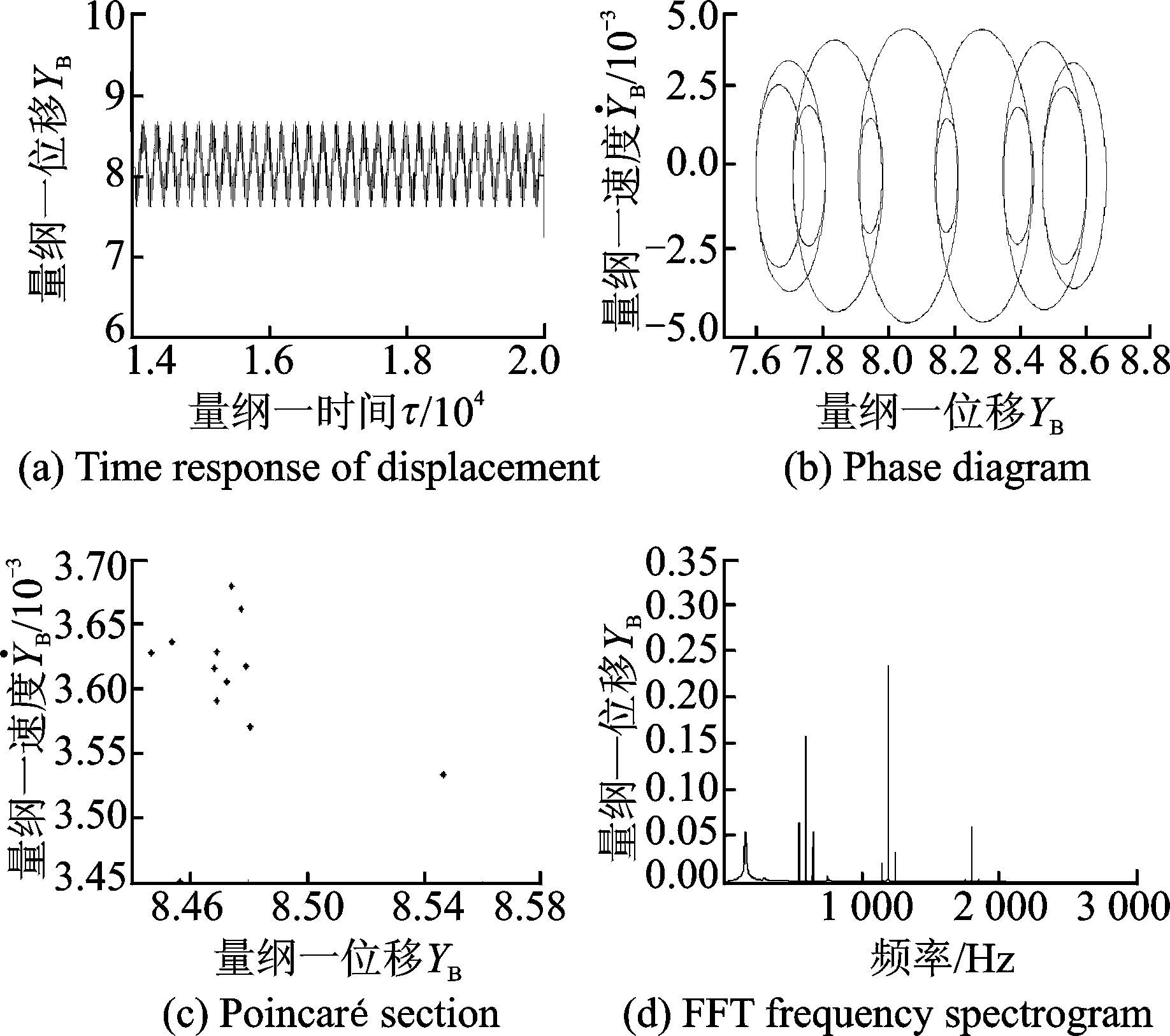
图 8 非时变支承刚度下YB的响应 Figure 8 Dynamic responses of YB under time-invariant supporting stiffness |
|
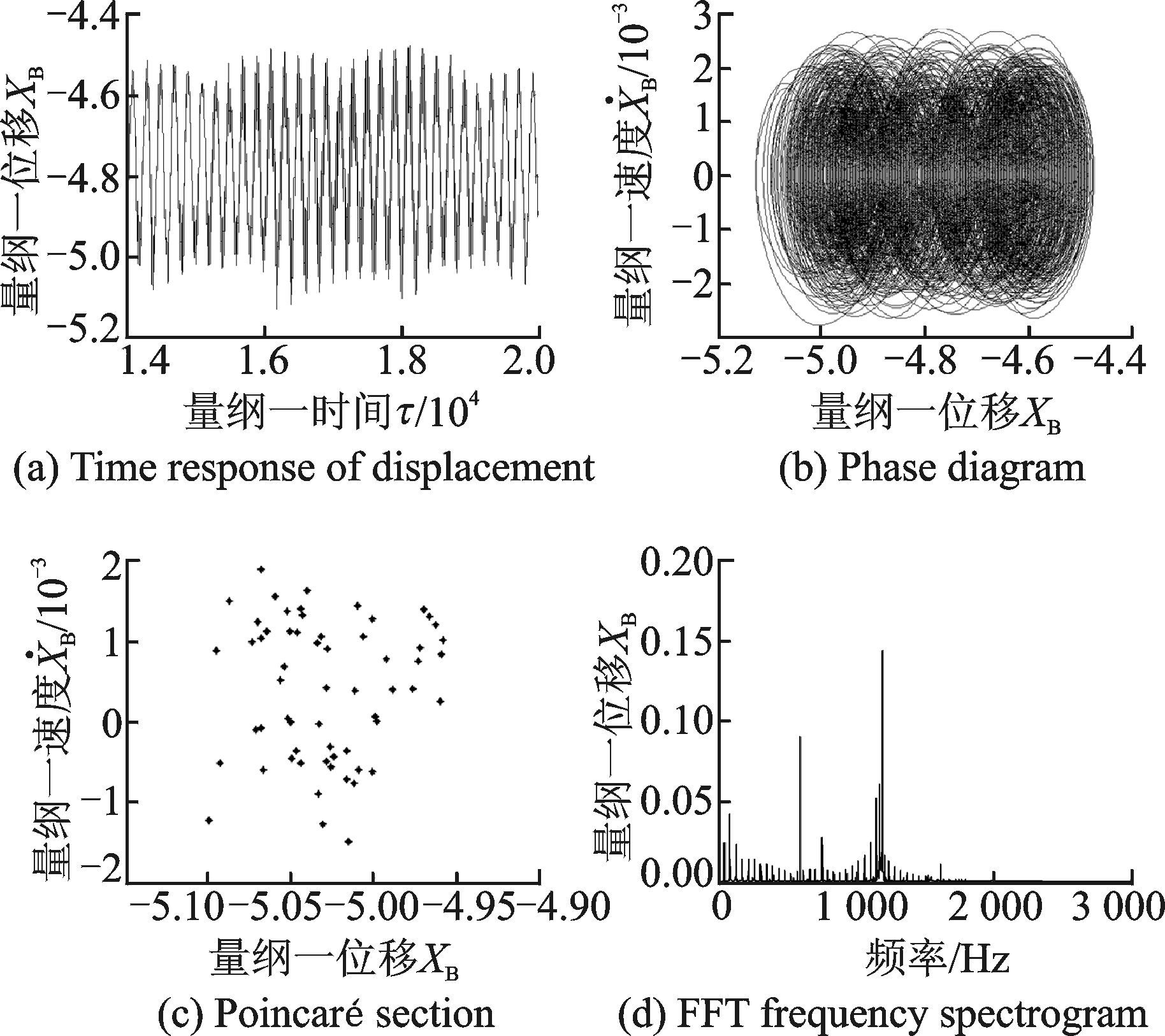
图 9 时变支承刚度下XB的响应 Figure 9 Dynamic responses of XB under time-variant supporting stiffness |
|
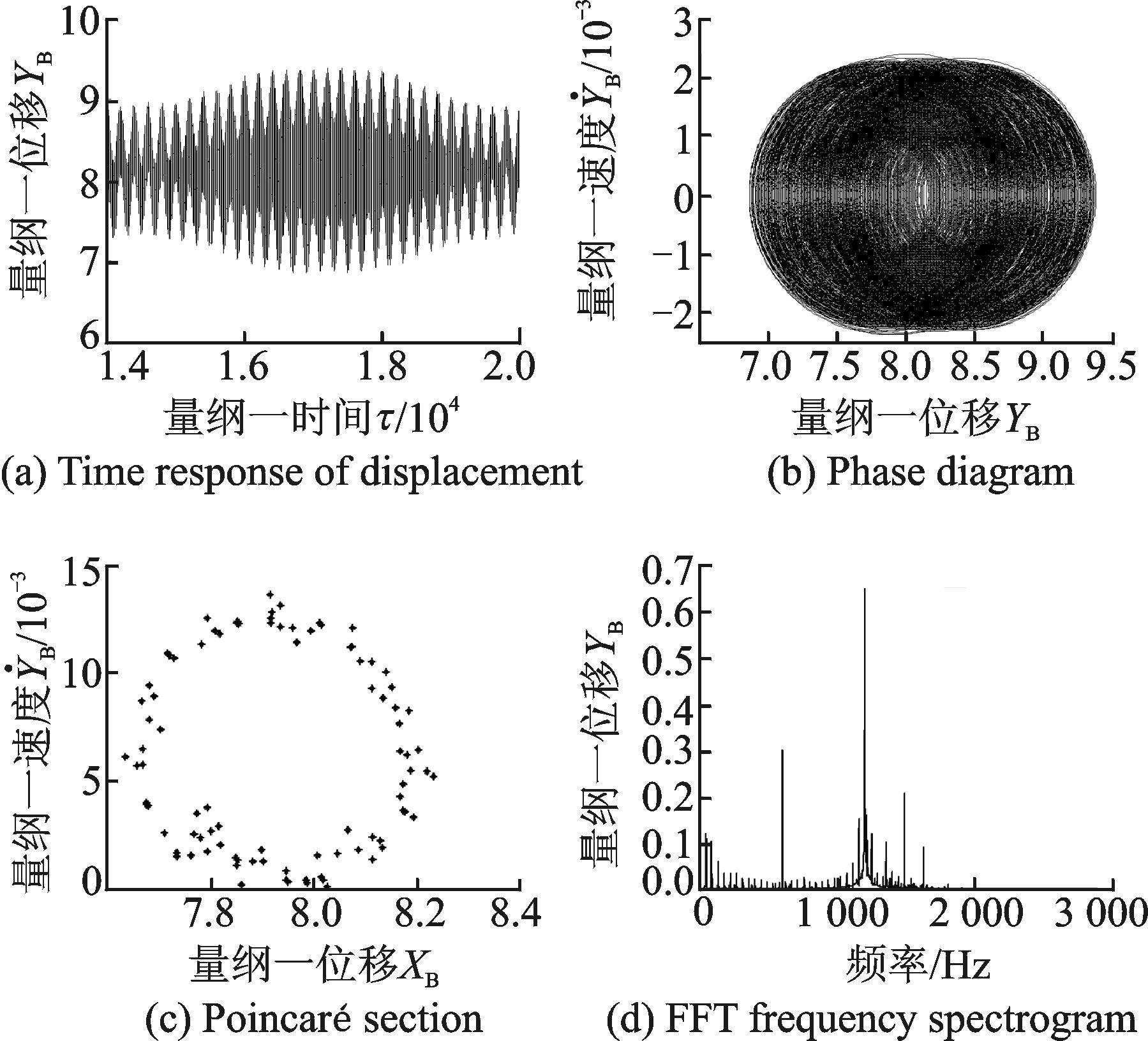
图 10 时变支承刚度下YB的响应 Figure 10 Dynamic responses of YB under time-variant supporting stiffness |
图 7和图 8所示为非时变支承刚度下输出轴上的横向振动位移的动态响应。由图可知,其稳态响应表现出近似周期变化的规律,相图是一系列近似椭圆叠加的封闭曲线,Poincaré映射图截面为12个离散点,FFT频谱离散地分布在各个频率上,不难判断出此时系统为多周期次谐波响应状态。
图 9和图 10所示为时变支承刚度下输出轴的动态响应。由图可知,其时间历程为非周期运动,相图为相互缠绕和交叉的曲线,Poincaré映射图截面为有限区域内、随机分布的点,FFT频谱则是有一定宽度的连续谱。因此可判断出,系统表现出强烈的非周期特性和非线性,处于混沌运动状态。
从图 7,8中的时间历程图可知,系统的响应十分平稳,输出轴横向振动位移在固定范围内波动。与图 9,10的结果对比发现,将时变支承刚度计入系统后,输出轴的位移响应幅值有一定幅度的增加,上下波动十分明显;输出轴y方向振动位移随时间的波动比x方向上的振动位移大,响应中出现“拍振”现象。
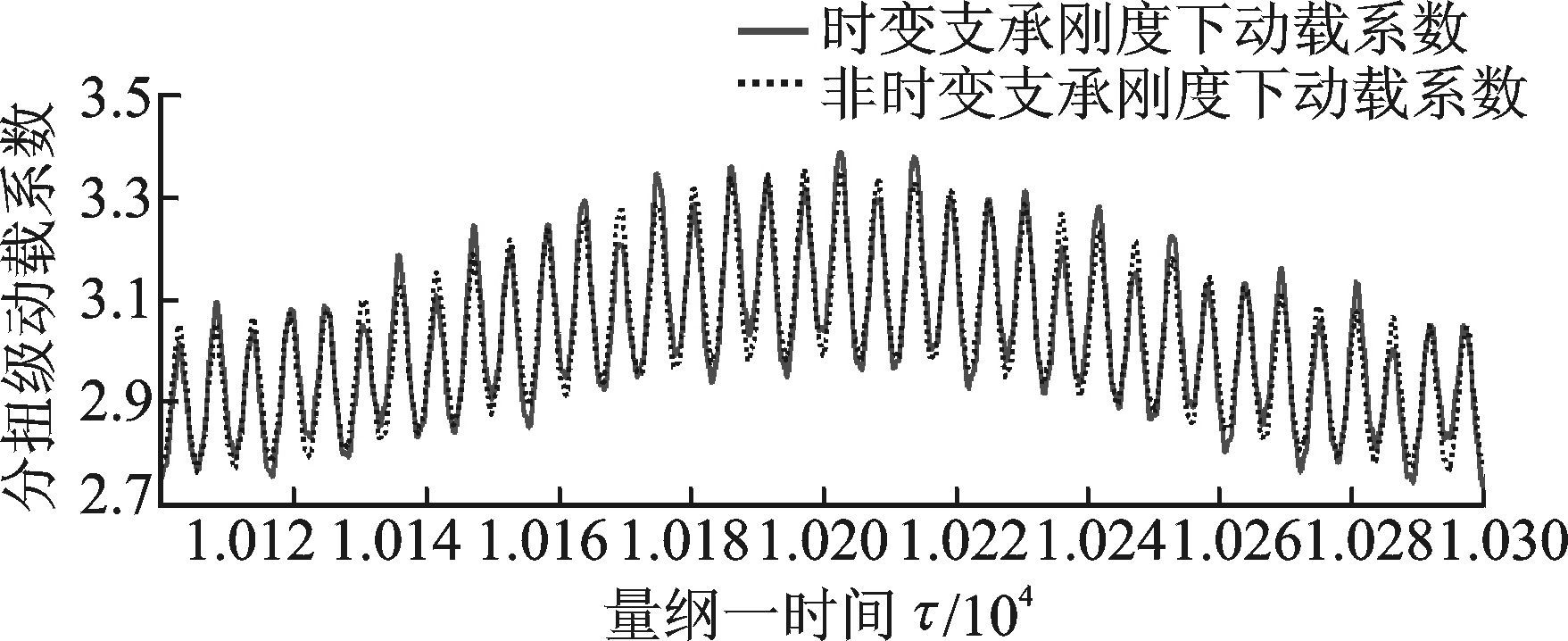
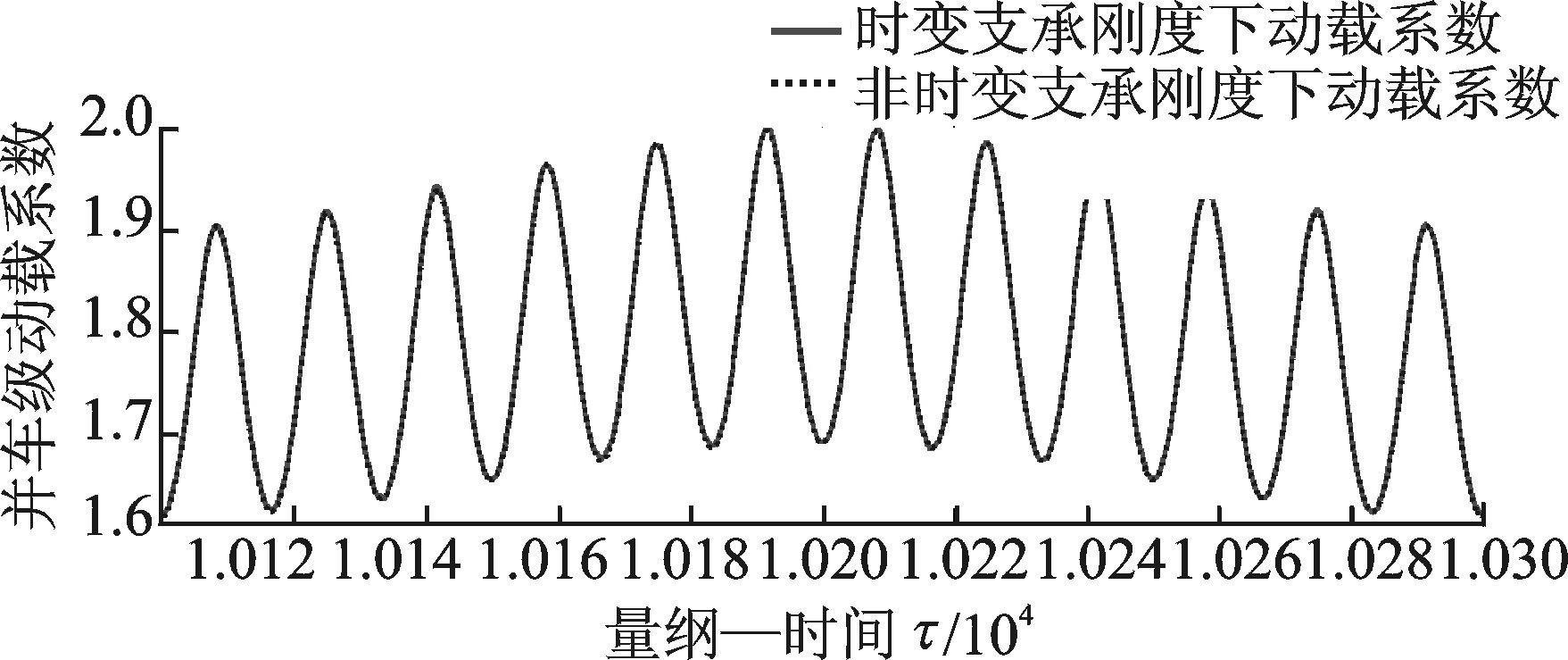
4.3 时变支承刚度对系统动载系数的影响图 11,12分别为分扭级和并车级的动载系数在一个波动周期内的时间历程图。从图 11,12可知,非时变支承刚度下,分扭级动载系数最大幅值为3.35,并车级动载系数最大幅值为1.998;时变支承刚度下,分扭级动载系数最大值为3.39,并车级动载系数最大值为2.003。相比非时变支承刚度,时变刚度下动载系数较大,且时变支承刚度对分扭级动载系数的影响较明显。
|
图 11 分扭级动载系数的时间历程 Figure 11 Time histories of dynamic load coefficient of split torque stages |
|
图 12 并车级动载系数的时间历程 Figure 12 Time histories of dynamic load coefficient of synthesized torque stages |
5 结论
本文推导了含时变支承刚度的齿轮分流传动系统的振动微分方程。通过将角位移转化为线位移,得到消除刚体位移后的动力学方程组,并采用龙格库塔法对动力学方程组进行求解,获得了该系统的动力学响应,进而开展了时变支承刚度和非时变支承刚度两种情况下系统动力学特性的对比分析。分析结果表明:
(1) 相对于非时变支承刚度而言,滚动轴承的时变支承刚度产生了4%左右的波动;
(2) 支承刚度的时变特性对该分扭传动系统的动力学特性,尤其是输出轴的横向振动产生一定影响。输出轴上的横向振动位移幅值增大了约5%;系统的非周期性和非线性增强,系统的稳定性变差。
(3) 在该圆柱齿轮分扭传动系统中,支承刚度的时变性会增大齿轮副间的动载系数,尤其是分扭级的动载系数;并且,与并车级相比,分扭级动载系数较大。
| [1] | White G. A lightweight split-torque transmission for a 330 kW helicopter[J]. Proceedings of the Institution of Mechanical Engineers, 1981, 196(1): 11–22. |
| [2] | White G. Design study of a 375 kW helicopter transmis-sion with split-torque epicyclic and bevel drive stages[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 1983, 197(4): 213–224. DOI:10.1243/PIME_PROC_1983_197_101_02 |
| [3] | Krantz T L. Dynamics of a split torque helicopter transmission[R]. NASA TM-106410, 1994. |
| [4] | Krantz T L, Rashidi M. Vibration analysis of a split path gearbox[C]//31st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. San Diego: American Institute of Aeronautics and Astronautics, 1995. |
| [5] | Zhao Xiahe, Le Haochang, Lan Liu. Free vibration characteristics on a split torque transmission[J]. Journal of Theoretical and Applied Information Technology, 2013, 47(2): 660–665. |
| [6] |
杨振. 转矩分流式齿轮传动系统动力学特性研究[D].西安:西北工业大学,2007: 40-84.
Yang Zhen. Dynamic characteristics of split-torque gear transmission system[D]. Xi'an: Northwestern Polytechnical University, 2007: 40-84. |
| [7] |
杨振, 王三民, 范叶森.
转矩分流式齿轮传动系统的非线性动力学特性[J]. 机械工程学报, 2008, 44(7): 52–57.
DOI:10.3901/JME.2008.07.052 Yang Zhen, Wang Sanmin, Fan Yesen. Nonlinear dynamic characteristics of split-torque gear transmission system[J]. Journal of Mechanical Engineering, 2008, 44(7): 52–57. DOI:10.3901/JME.2008.07.052 |
| [8] |
杜佳佳, 王三民, 王颖.
功率双分支传动系统的动力学特性研究[J]. 机械制造, 2012, 50(4): 10–12.
Du Jiajia, Wang Sanmin, Wang Ying. Research on dynamic characteristics of the dual power path gear transmission[J]. Machinery, 2012, 50(4): 10–12. |
| [9] |
桂永方, 朱如鹏, 扶碧波, 等.
扭转刚度对双输入齿轮分流传动系统动力学均载系数的影响[J]. 航空动力学报, 2014, 29(9): 2265–2268.
Gui Yongfang, Zhu Rupeng, Fu Bibo, et al. Impact of torsional stiffness on dynamic load sharing of cylindrical gear split-torque transmission system[J]. Journal of Aerospace Power, 2014, 29(9): 2265–2268. |
| [10] |
董金城, 王三民, 林何, 等.
参数对二分支斜齿轮传动动载和均载特性影响[J]. 航空动力学报, 2015, 30(5): 1260–1266.
Dong Jincheng, Wang Sanmin, Lin He, et al. Parameters effect on dual-path helical gear transmission dynamic load and load sharing characteristic[J]. Journal of Aerospace Power, 2015, 30(5): 1260–1266. |
| [11] |
董皓, 马晨, 方舟, 等.
考虑实际齿面的功率四分支传动系统动态分析[J]. 南京航空航天大学学报, 2015, 47(1): 132–138.
Dong Hao, Ma Chen, Fang Zhou, et al. Dynamic analysis of power four-branching transmission considering actual tooth surface features[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(1): 132–138. |
| [12] | Liew H V, Lim T C. Analysis of time-varying rolling element bearing characteristics[J]. Journal of sound and vibration, 2005, 283. |
| [13] | 邓四二, 贾群义. 滚动轴承设计原理[M]. 北京: 中国标准出版社, 2008: 111-116. |
| [14] | Sawalhi N, Randall R B. Simulating gear and bearing interactions in the presence of faults: part I. the combined gear bearing dynamic model and the simulation of localized bearing faults[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1924–1951. DOI:10.1016/j.ymssp.2007.12.001 |
| [15] | Lioulios A N, Antoniadis I A. Effect of rotational speed fluctuations on the dynamic behavior of rolling element bearings with radial clearances[J]. International Journal of Mechanical Sciences, 2006, 48(8): 809–829. DOI:10.1016/j.ijmecsci.2006.03.006 |
 2016, Vol. 48
2016, Vol. 48


